Evaluation of ride performance of PID controller in active suspension systems for an electric vehicle

1. Introduction

Vehicle vibrations have a significant impact on the ride comfort and safety of electric vehicles (EVs). The suspension system is well-known for its critical role in absorbing these vibrations to enhance ride quality and vehicle safety. L. V. Quynh et al. [1] analyzed and compared the vibration suppression effectiveness for in-wheel motor, taking into account the motor suspension system. Unlike passive, semi-active, and active suspension systems (PSSs, S-ASSs, ASSs) offer greater flexibility to respond to unpredictable forces arising from road surface roughness and vehicle load, even while driving. To achieve this level of performance, various control algorithms have been applied to ASSs to ensure that the vehicle maintains optimal comfort and stability. For example, Maurya et al. [2] applied a LQR (Linear Quadratic Regulator) LQR controller for an ASS to enhance vehicle ride comfort and stability. While the LQR controller demonstrated improvements in vehicle performance, it had limitations, particularly in terms of robustness under varying conditions, and its performance could degraded when the model parameters change or are uncertain. Salem, et al. [3] proposed using a FLC (Fuzzy Logic Controller) for ASSs to suppress vibrations. However, the design of FLC demanded significant expertise and experience from the designer, as the performance heavily relies on the quality of the rule base and membership functions defined. Chen et al. [4] investigated the H∞ control strategy for ASSs. However, the complexity of designing an H∞ controller required a well-defined system model and could be computationally intensive, making it less practical for real-time applications. Kim et al. [5] analyzed the performance of an ASS using a SMC (Sliding Mode Controller), and the results showed significant improvements over PSSs. However, SMC was sensitive to system noise. Mehra et al. [6] introduced a new MPC (Model Predictive Control) design for ASSs. Nonetheless, it requires high computational power and a precise system model to predict future states accurately, which may not always be feasible in real-time vehicle applications. Van Thoan, T. et al. [7], [20] proposed PID controller for DWSPs (Driving Wheel Slip Prevention System) of a dump truck. Kumar et al. [8] presented a comparative study between PSSs and ASSs using a PID controller, demonstrating improved ride comfort and vehicle stability. In another study, Youness et al. [9] proposed a PID control strategy for an ASSs using a full vehicle model. The findings showed that the PID controller could effectively reduce vibrations and improve overall vehicle performance. For optimizing the functionality of the PID controller, various optimization algorithms and hybrid control strategies have been employed alongside the PID controller. For examples, Di Tan et al. [10] optimized the parameters of a PID controller for ASS using PSO (Particle Swarm Optimization), achieving improved system performance. Similarly, Boulaaras et al. [11] adjusted the proportional, integral, and derivative gains by implementing a GA (Genetic Algorithm), which reduced the workload for users and led to enhanced system quality. Xinjie et al. [12] researched a FLC around PID methodology for ASSs. However, using hybrid controllers or optimization algorithms remains a challenge. L. V. Quynh et al. [13] suggested a control strategy for damping on electric vehicle using a MSC (Modified Skyhook Controller). The flexibility of the suspension system was demonstrated by its effectiveness. In addition, several other control algorithms [14], [16-19] applied to control S-ASSs or semi-active mounting systems to improve their efficiency. In this study, The PID Controller is designed for EV ASSs to improve EV ride comfort via a full EV dynamic model.

2. EV dynamic model

2.1. Full EV dynamic model

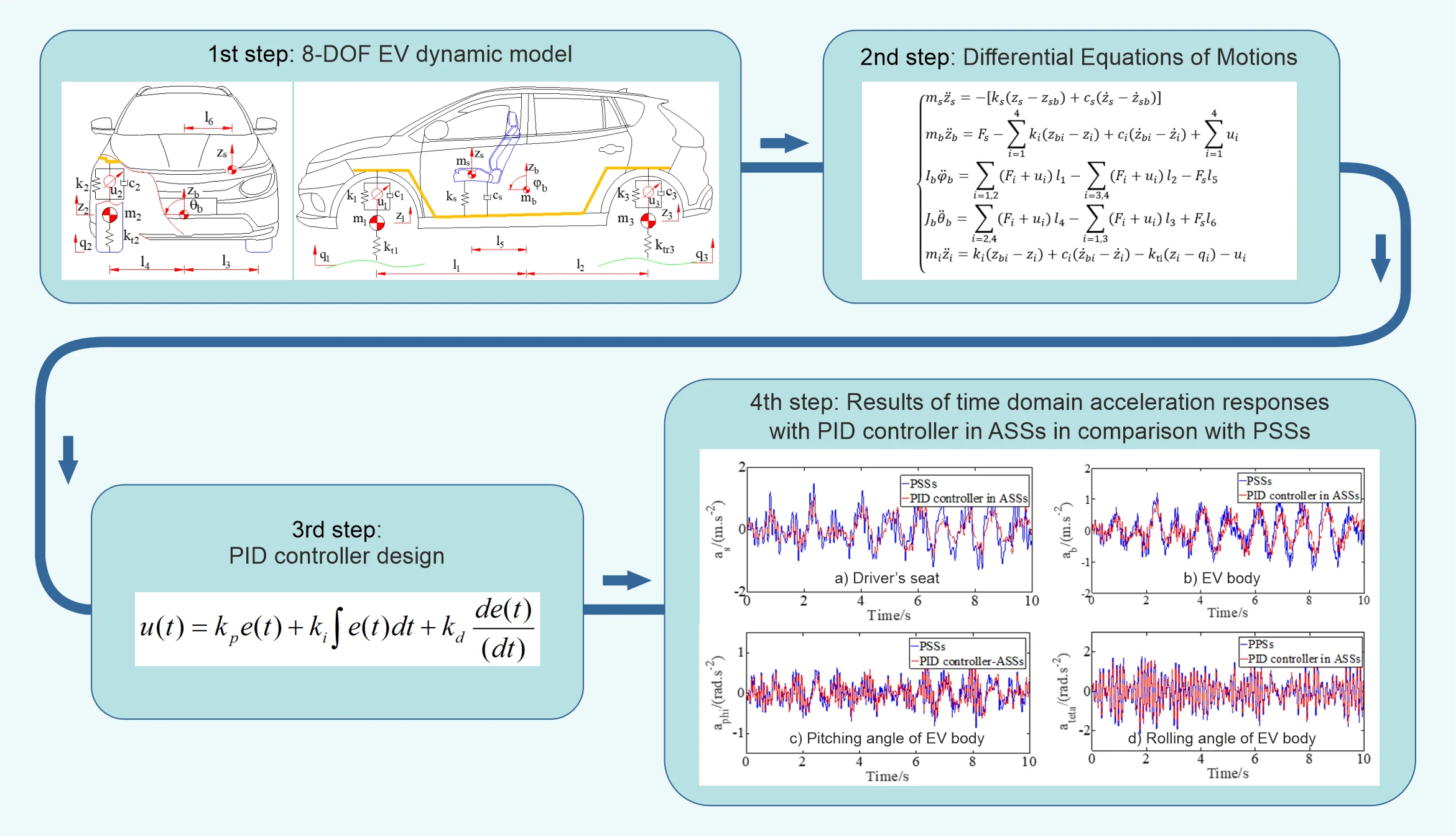
A detailed 8-DOF (Degrees Of Freedom) EV dynamic model is employed to evaluate the ride performance of ASS, as illustrated in Fig. 1.

Fig. 18-DOF EV dynamic model

The vehicle model comprises the following parameters, $m_s$, $m_b$ and $m_i$ are denoted by the masses of driver’s seat, EV body, and axle masses, respectively; $c_s$ and $c_i$ are denoted by the damping coefficients of driver’s seat PSS and EV PSSs, respectively; $k_s$, and $k_i$ are denoted by the spring stiffness coefficients of driver’s seat PSS and EV PSSs, respectively; $k_{ti}$ are denoted by the damping and stiffness coefficients of tires, respectively; $u_i$ are denoted by the suspension control signals from the actuator that generate the forces between the body and axles of EV; $l_j$ are the distances; $z_i$ and $z_b$ are denoted by the vertical displacement of EV axles and EV body, $\phi$ and $\theta$ are denoted by the angular displacements of EV body; q_i aredenoted by the vertical displacement due to road surface excitations ($i=$1-4 and $j=$1-6). Motion is frequently described using Jourdain’s principle [19] and the classic Newton-Euler method, Newton-Euler’s principle applied to the system results in the following differential equations of motion:

1

$\left\{\begin{array}{l}{m}_s{\ddot{z}}_s=-{[k}_s(z_s-z_{sb})+c_s({\dot{z}}_s-{\dot{z}}_{sb})],\\ m_b{\ddot{z}}_b=F_s-{\sum }_{i=1}^4{k}_i\left(z_{bi}-z_i\right)+c_i\left({\dot{z}}_{bi}-{\dot{z}}_i\right)+{\sum }_{i=1}^4{u}_i,\\ I_b{\ddot{\phi }}_b={\sum }_{i=\mathrm{1,2}}\left(F_i+u_i\right)l_1-{\sum }_{i=\mathrm{3,4}}\left(F_i+u_i\right)l_2-F_s{l}_5,\\ J_b{\ddot{\theta }}_b={\sum }_{i=\mathrm{2,4}}\left(F_i+u_i\right)l_4-{\sum }_{i=\mathrm{1,3}}\left(F_i+u_i\right)l_3+F_s{l}_6,\\ m_i{\ddot{z}}_i=k_i(z_{bi}-z_i)+c_i({\dot{z}}_{bi}-{\dot{z}}_i)-k_{\text{ti}}(z_i-q_i)-u_i,\end{array}\right.$

where, $I_b$ and $J_b$ are the inertia moments of EV body mass; $z_{bi}$ and $z_{sb}$ are the zero-bias points of EV body and driver’s seat which are determined by Eq. (2):

2

$z_{b1}=z_b-l_1{\phi }_b+l_3{\theta }_b,z_{b3}=z_b+l_2{\phi }_b+l_3{\theta }_b,z_{b2}=z_b-l_1{\phi }_b-l_4{\theta }_b,$
$z_{b4}=z_b+l_2{\phi }_b-l_4{\theta }_b,z_{sb}=z_b-l_5{\phi }_b+l_6{\theta }_b.$

3. PID controller design

The PID controller, one of the most common feedback controllers, works by continuously adjusting control efforts based on the error signal. The general PID control equation is:

where, $u\left(t\right)$ is denoted by the control signal, $e\left(t\right)$ is denoted by the error, and $k_p$, $k_i$, and $k_d$ are denoted by the proportional, integral, and derivative gains.

The input signal plays a crucial role in the controller efficiency. Therefore, in this study, the feedback signal is chosen as the relative displacements of ASSs, $z_t$, serving as the input for the controller. The output consists of the controller’s parameters, including $k_p$, $k_i$, and $k_d$. By selecting suspension displacement as the input, the system could effectively adjust to change, ensuring the optimal performance. Eq. (4) could be rewritten as follows:

To enhance control performance under survey operating condition, the Ziegler-Nichols approach has been used to determine the parameters of PID controller. The full EV dynamic model comprises with four suspensions, each requiring a dedicated PID controller. Despite the need for multiple controllers, their design process is analogous. Therefore, using the Ziegler-Nichols technique to optimize the proportional gains of the PID controller [23], [24], the controller parameters obtained are $k_p=$ 41050, $k_i=$ 3572, and $k_d=$ 193.

4. Results and discussion

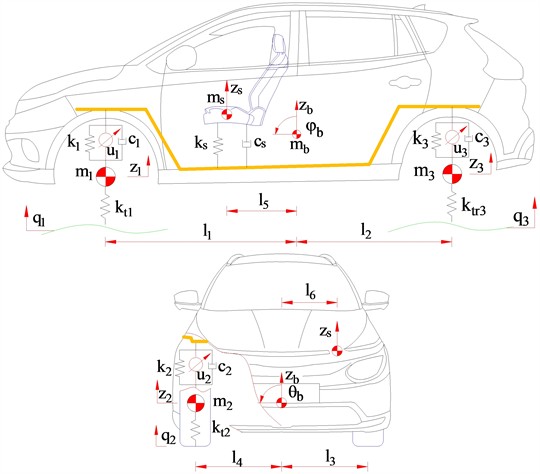
The ride performance of ASSs with the PID controller is investigated and compared PSSs when vehicle moves on road surface ISO class C at EV speed of $v=$20 m/s and full load of EV. The parameters of the PID controller obtained after optimization which are used as input for the control signals of ASSs. Eq. (1) and the PID controller are simulated in Matlab/simulink environment with EV parameters in Table 1. The vertical driver’s seat, vehicle body, pitching and rolling acceleration responses ($a_s$, $a_b$, $a_{phi}$ and $a_{teta}$) with PID controller in ASSs in comparison with PSSs are shown in Fig. 2 when vehicle moves under the above survey condition.

The results in Fig. 2 show that the maximum amplitude values of $a_s$, $a_b$, $a_{phi}$ and $a_{teta}$ with PID controler in ASSs decrease very strongly compared to PSSs, which means that proposed controller for EV ASSs has significantly improved vehicle ride comfort. From the results of Fig. 2, $a_{ws}$, $a_{wb}$, $a_{wphi}$ and $a_{wteta}$ values are defined based on ISO 2631 (1997) [25] and $a_{ws}$, $a_{wb}$, $a_{wphi}$ and $a_{wteta}$ values with PID controller in ASSs in comparison with PSSs are shown in Table 2. The comparative results of Table 2 indicate that $a_{ws}$, $a_{wb}$, $a_{wphi}$ and $a_{wteta}$ values with PID controller ASSs respectively reduce by 31.12 %, 24.76 %, 15.00 %, and 11.59 % in comparison with PSSs under the above survey condition, which means that the proposed controller performance for EV ASSs significantly improves vehicle ride comfort compared to PSSs.

Fig. 2Results of time domain acceleration responses with PID controller in ASSs in comparison with PSSs

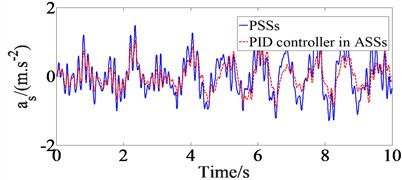
a) Driver’s seat

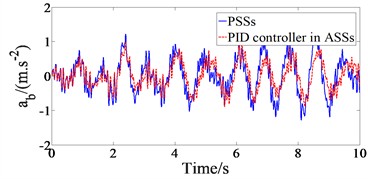
b) EV body

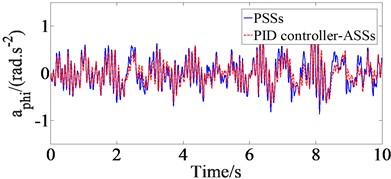
c) Pitching angle of EV body

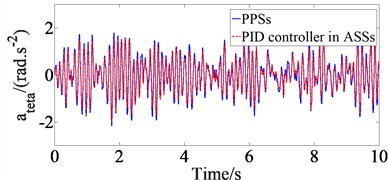
d) Rolling angle of EV body

5. Conclusions

In this study, a 8 -DOF full dynamic model of EV is proposed for control ASSs using PID controller towards enhancing ride comfort. The parameters of the PID controller are tuned using the Ziegler-Nichols method. The motion equations of EV and the combined PID controller are all implemented in the Matlab/Simulink software environment. The obtained results have shown that the maximum amplitude values of $a_s$, $a_b$, $a_{phi}$ and $a_{teta}$ with PID controller in ASSs decrease very strongly compared to PSSs when vehicle moves on road surface ISO class C at EV speed of $v=$20 m/s and full load of EV. Finally, $a_{ws}$, $a_{wb}$, $a_{wphi}$ and $a_{wteta}$ values with PID controller ASSs respectively reduce by 31.12 %, 24.76 %, 15.00 %, and 11.59 % in comparison with PSSs under the above survey condition, which means that the proposed controller performance for EV ASSs significantly improves vehicle ride comfort compared to PSSs.