Nonlinear vibration and transient stress analysis of disc brake based on computer simulation technology

2.1. Model establishment and simplification

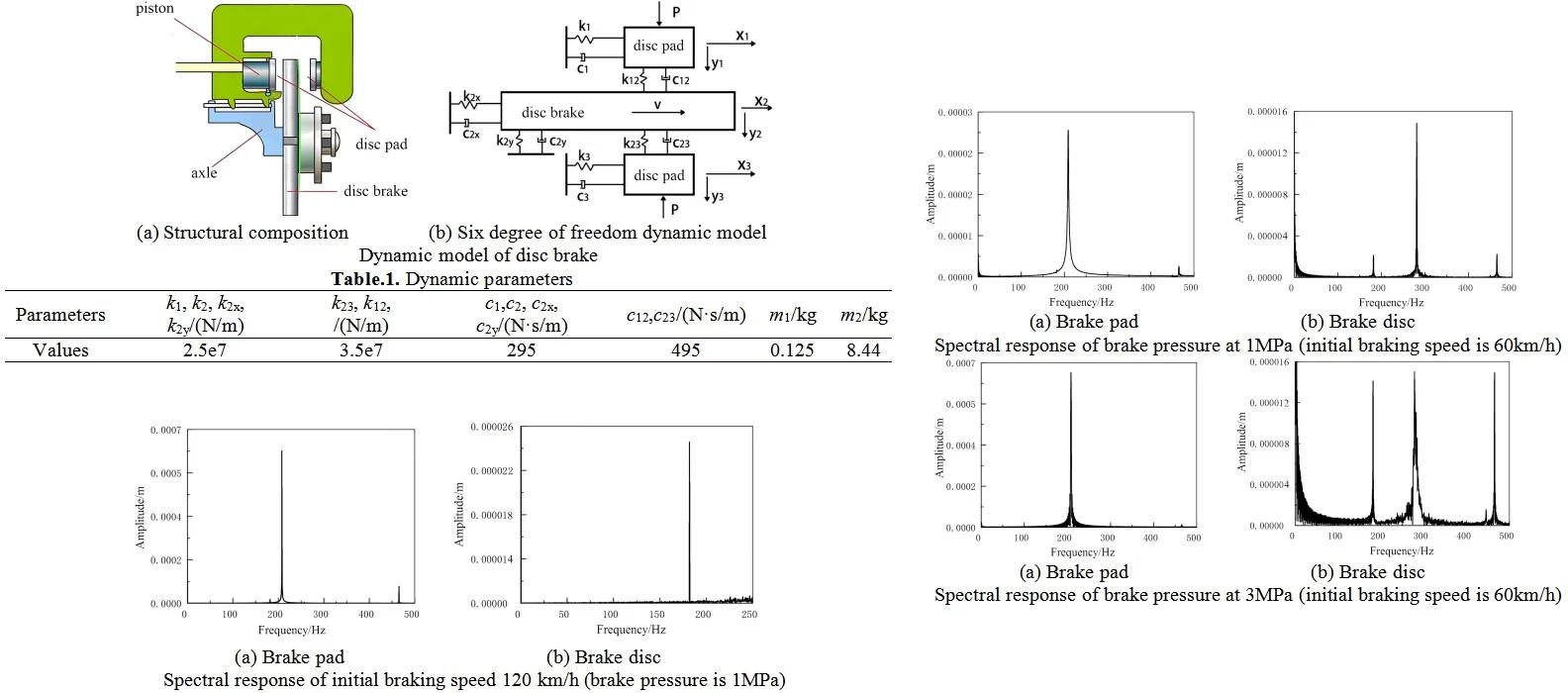
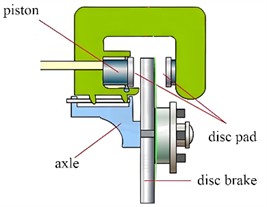
Typically, disc brake is composed of brake caliper body, brake pad, brake disc, and piston as shown in Fig. 1(a). The brake disc is made of alloy steel and fixed on the wheel, rotating with the wheel. The cylinder is fixed on the bottom plate of the brake and remains stationary. They move together with the piston and apply braking force to the brake disc after friction with the brake disc. Based on the installation method and working state of the disc brake [6], a dynamic model with multi degree of freedom characteristics is constructed and analyzed, as shown in Fig. 1(b). Under ideal conditions, assuming that the quality and structure of the different parts are balanced. The mass of the fixed friction plate, brake disc, and movable friction plate is $m_1$, $m_2$, and $m_3$, respectively. The supporting stiffness of the upper and lower friction plates are $k_1$ and $k_3$, respectively, and the damping $c_1$ and $c_3$ are equal to each other. The contact attributes of the friction pair surface can be expressed as $k_{12}$, $c_{12}$, $k_{23}$, $c_{23}$, $k_{2x}$, $k_{2y}$, $c_{2x}$, $c_{2y}$ respectively. Let the horizontal displacement of brake pads and brake discs be $x_1$, $x_2$, and $x_3$. The normal displacements are $y_1$, $y_2$, and $y_3$.

Fig. 1Dynamic model of disc brake

a) Structural composition

b) Six degree of freedom dynamic model

2.2. Vibration response under different braking conditions

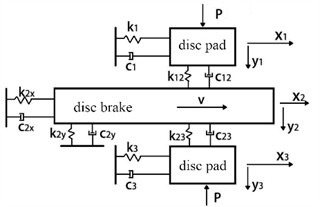
(1) The influence of brake pressure on vibration. Under different brake pressure load conditions, the amplitude frequency response results of the vibration process of brake pads and brake discs can be calculated, as shown in Fig. 2 and Fig. 3, respectively. It can be inferred that within the maximum external excitation frequency range, the main frequencies of resonance between brake pads and brake discs are different, at 210 and 300 Hz, respectively. The brake pressure has a significant impact on the frequency response. If the braking pressure is increased, the feedback generated by the excitation vibration will be more significant, because the contact stiffness and damping have chaotic characteristics, which are one of the key factors affecting the amplitude.

Fig. 2Spectral response of brake pressure at 1 MPa (initial braking speed is 60 km/h)

a) Brake pad

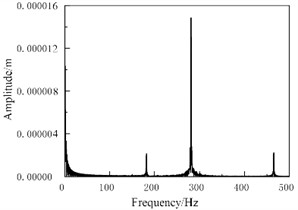
b) Brake disc

Fig. 3Spectral response of brake pressure at 3 MPa (initial braking speed is 60 km/h)

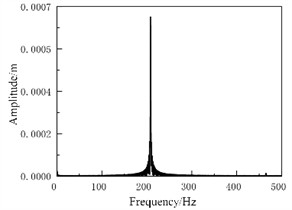
a) Brake pad

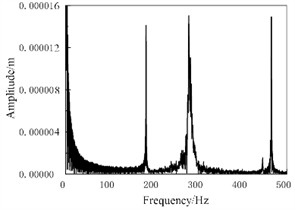
b) Brake disc

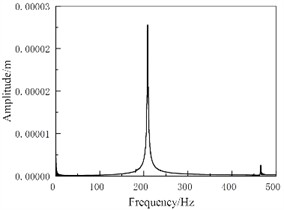
(2) The influence of initial braking speed on vibration. Under the condition of initial braking speed of 120 km/h, the spectral response results are shown in Fig. 4. It can be seen that as the initial braking speed increases, the vibration frequency gradually concentrates towards the main frequency, the main vibration frequency gradually protrudes, and the amplitude gradually increases. This is because as the initial braking speed gradually increases, the period of the system’s stick slip vibration will shorten, and the slope of the displacement growth of the brake pad during the adhesion stage will increase. When the speed increases to a certain extent, the stick slip motion gradually evolves into pure slip motion, and vibrations different from the main frequency also disappear.

Fig. 4Spectral response of initial braking speed 120 km/h (brake pressure is 1 MPa)

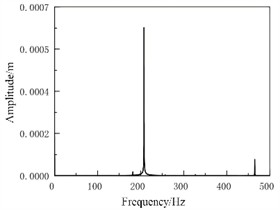
a) Brake pad

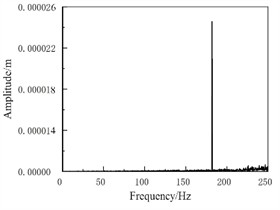
b) Brake disc

2.3. Modal calculation and discussion

The simulation results of modal shapes are shown in Fig. 5. It can be seen that the maximum displacement of each modal vibration mode of the brake disc occurs at the circumferential edge of the disc perpendicular to the pitch direction, and the part where the maximum displacement occurs is symmetrically distributed on the brake disc. As the modal order increases, the number of pitch diameters of the brake disc also increases, and the brake disc is divided into more deformation intervals. However, the overall displacement and pitch diameter distribution of the brake disc are roughly similar, symmetrically distributed along the radial axis passing through the center of the disc. The maximum displacement difference between the modal shapes of each order is relatively small, which is due to the increase in brake disc frequency, resulting in an increase in the number of brake disc pitch diameters. The brake disc vibration modes are divided into smaller intervals, thereby weakening the influence on the deformation displacement of the brake disc.

The experimental mode adopts laser testing method, which requires fixing the brake disc on the test bench and applying excitation to the brake disc using an exciter, as shown in Fig. 6. The microphone transmits the vibration signal of the brake disc to the computer, and the laser vibrometer transmits the modal vibration signal of the brake disc to the computer. The collected signal is processed by the computer to obtain the modal frequency of the brake disc. The comparison between the experimental test results and the simulation results is shown in Table 2. It can be seen that the error between the modal test and modal analysis frequency of the brake disc is within 5.1 %, which is within a controllable range. Therefore, the finite element model of the disc brake established is accurate.

Fig. 5Modal shapes

a) The first order

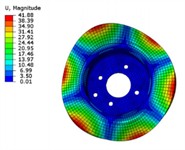
b) The second order

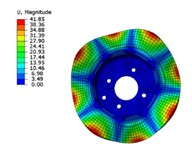
c) The third order

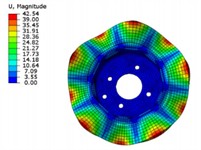
d) The fourth order

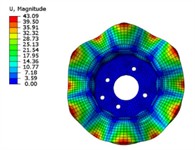
e) The fifth order

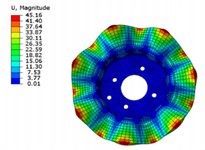
e) The sixth order

Fig. 6Modal testing scheme

3.1. The establishment of thermal machine coupling model

Early research on brake friction was mainly conducted through experimental methods. However, due to the complex and variable actual working conditions, the reproducibility of experimental research is poor and the cost is high. Establish the finite element model of the friction pair as shown in Fig. 7(a), using hexahedral scanning method for mesh division and local refinement, and selecting temperature and displacement coupling as the analysis module. During the braking process, the contact surface of the friction pair mainly conducts heat. Introduce heat flux density into the friction contact area between the brake disc and brake pad, and apply boundary conditions on the non-contact surface of the model. When the brake pads and brake discs rub against each other during braking, the speed of heat conduction inside the object is lower than the speed of heat generated by friction, resulting in a temperature gradient on the brake disc surface and varying degrees of thermal deformation of the brake disc unit, leading to uneven stress distribution on the brake disc. So it is necessary to choose a suitable material with a thermal conductivity coefficient to achieve temperature transmission between the contact and non-contact areas, which is more in line with reality and increases the realism of the simulation.

When the brake pad comes into contact with the brake disc, the brake pad can only move in the normal direction of the contact surface, while the brake disc can rotate in the normal direction and be fixed in other directions to ensure sufficient friction between the brake pad and the brake disc. The magnitude of the friction coefficient is related to temperature changes, while the magnitude of the friction force is determined by the friction coefficient and the pressure applied to the brake pads. For the motion of the friction pair, a coupling node is established at the center of the brake disc using degrees of freedom constraints. Couple the node with the surrounding protrusions and set the rotational angular velocity of the point to achieve the rotation of the brake disc. Apply a load on the surface of two brake pads to simulate the actual braking force, so that the brake pads and brake discs are in contact with each other, and achieve frictional braking when the brake discs rotate. To analyze the variation law of dynamic stress in different directions, two paths are set up, as shown in Fig. 7(b) and Fig. 7(c), respectively.

Fig. 7The establishment of FEA model and path setting

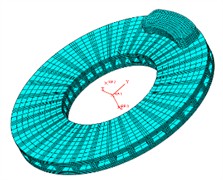
a) Model of the friction pair

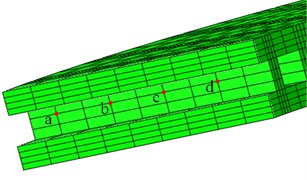
b) Path in rib direction

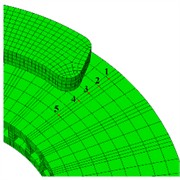
c) Path in end face direction

3.2. Discussion of transient stress results

The transient stress field cloud map of the brake at different time intervals is illustrated in Fig. 7. It is evident that the hot spot phenomenon within the stress distribution is quite pronounced. Key factors affecting this stress field include pressure, friction, and temperature, with the peak stress consistently found on the friction surface. Following 1th second, the forces acting between the friction pairs are released, leading to a situation where temperature changes primarily dictate the characteristics of the stress field observed at that moment. At 10th second, the maximum stress value remains approximately on the order of 10⁷. The dynamic distribution of residual stresses can reflect the degree of equilibrium in surface deformation. If the magnitude and gradient of residual stress are small, this will be beneficial in reducing the noise and vibration of the friction pair.

Fig. 8Transient stress results

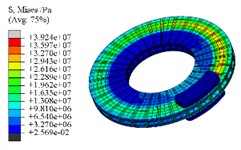
a) 0.5 s

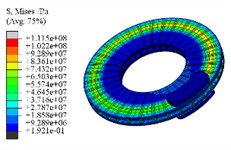
b) 1.0 s

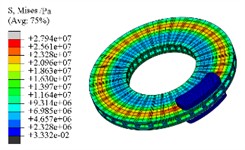
c) 5 s

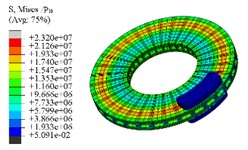
d) 10 s

The stress curves of the brake disc in the time domain for various paths are illustrated in Fig. 9. It is evident that throughout the braking process, the stress at the friction surface nodes (nodes 1 to 4) displays a sawtooth-like upward trend in the radial direction, with node 2, located at the center of the brake pad, experiencing the highest stress levels. In the interval from 0 to 1 second, node 5 shows quite significant fluctuations in stress. However, its distance from the friction surface results in it maintaining a relatively low value. The stress variation law of the end face path markedly differs from that of the rib face, particularly during the braking stage, where the phenomenon of stress mutation is highly conspicuous. This is because the brake pads have a direct compressive impact on the ribs. When the brake pads pass over this node, the stress instantaneously decreases with virtually no time-delay phenomenon. After the brake pressure is released, the stress at node d gradually increases to a stable state, while the stress at nodes a to c sharply declines and gradually stabilizes. Due to the distance of node d from the heat source, its temperature keeps rising. Under the condition where stress is dominated by temperature, the stress of node d is greater than that of nodes a to c.

Fig. 9Stress changes on different paths

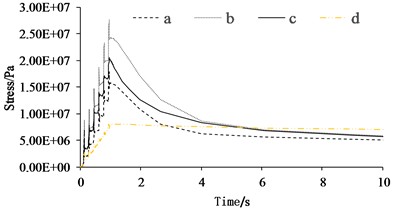
a) Path in rib direction

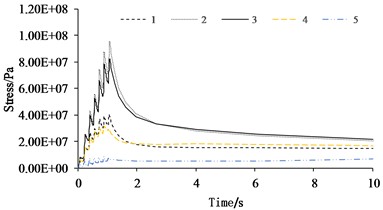
b) Path in end face direction