Optimal control of lane changing problem of intelligent vehicle

Liu, Yingjie; Cui, Dawei; Xie, Chenglian

doi:10.21595/jve.2024.24462

Journal of Vibroengineering

Browse Journal

Submit article

Published: 18 January 2025

Check for updates

Optimal control of lane changing problem of intelligent vehicle

Yingjie Liu¹

Dawei Cui²

Chenglian Xie³

¹Huzhou Key Laboratory of Urban Multidimensional Perception and Intelligent Computing, Huzhou, 313000, P. R. China

^{1, 2}School of Machinery and Automation, Weifang University, Weifang, 261061, Shandong, China

³Shandong Industrial Technician College, Weifang 261053, Shandong, China

Corresponding Author:

Yingjie Liu

Cite the article Download PDF

Article in Press

Downloads 7

Abstract

Lanes changing is one of the basic behaviors of vehicle driving, which has a significant impact on road traffic safety and stability. Aiming at the problem of slow convergence rate in solving the optimal control problem of vehicle lane changing, an optimal lane changing control method based on hp adaptive pseudospectral method is proposed. By establishing a vehicle kinematic model, boundary constraints, and path constraints, combining with the physical process of vehicle lane changing the proposed method discretizes the control and state variables to transform the multi constraint optimal control problem into a nonlinear programming problem and the minimum vehicle lane changing time is set as the performance objective function. And also, the proposed method is compared with traditional solving methods. The simulation results show that the proposed method can effectively solve the optimal feasible lane changing trajectory and complete the lane changing maneuver process in the shortest possible time.

Optimal control of lane changing problem of intelligent vehicle

Highlights

The proposed method can effectively solve the optimal feasible lane changing trajectory.
The proposed method can control the vehicle complete the lane changing maneuver process in the shortest possible time.
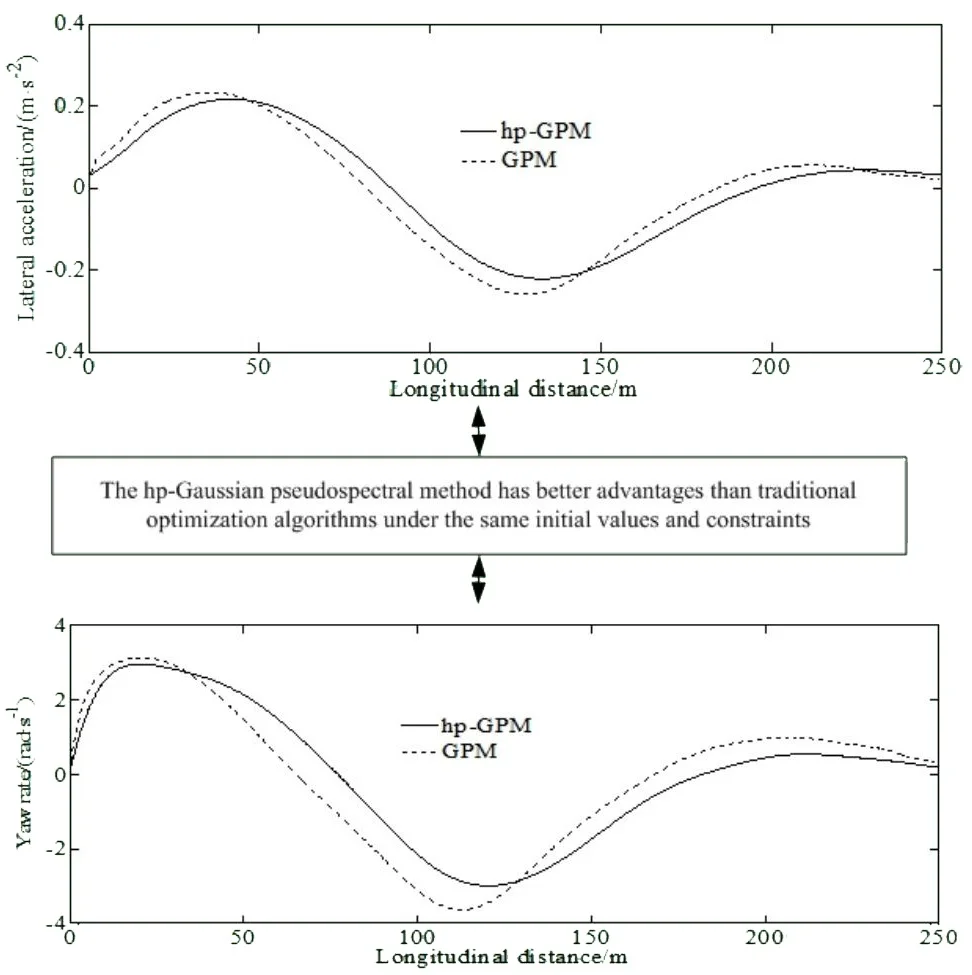
The hp Gaussian pseudospectral method has better advantages than traditional optimization algorithms under the same initial values and constraints.

1. Introduction

The rapid increase in the number of vehicles has also brought about problems such as low traffic efficiency and frequent traffic accidents. Frequent traffic accidents are often caused by improper operation of the drivers when changing lanes. Vehicle lane changing behavior is also one of the common research focuses in the field of autonomous driving. Lane changing behavior is a decision-making behavior with many influencing factors in the process of autonomous driving. The driving state of the driver and the vehicle itself during the driving process will affect the comfort and safety of the vehicle during the lane changing process. When changing lanes, the driver needs to first observe the driving environment and then change lanes based on their previous driving experience. Implementing lane change safety decisions in autonomous driving of vehicles can not only improve traffic efficiency, but also reduce the incidence of traffic accidents. Nowadays, lane changing behavior decision-making for autonomous vehicles is also a focus of research in both academia and industry. Although there has been a qualitative leap in lane changing technology for autonomous vehicles, there are still a series of problems. In recent years, as economic development level has continued to grow, and the per capita number of motor vehicles has also been increasing. However, at the same time, it also faces very serious road traffic safety problems. According to statistics, over 90 % of them occur during the lane change process. Therefore, achieving autonomous lane changing control for vehicles is an extremely important aspect of autonomous driving. When autonomous vehicles are driving on multi lane roads, the entire decision-making process of changing lanes to the optimal target lane through autonomous operation is called autonomous driving lane changing behavior. Forced lane changing is when the external traffic environment hinders the normal operation of vehicles and requires lane changing, and vehicles must complete the lane changing operation before the latest lane changing position. Free lane changing is subjectively a voluntary lane change to meet speed expectations and efficiently complete the driving process. The purpose of changing lanes is to improve current driving conditions, with a certain degree of autonomy and non necessity. The decision to change lanes is influenced by the road traffic environment, and sometimes may be abandoned due to the influence of the traffic environment. Vehicle lane changing is a widely occurring behavior during driving, and improper lane changing behavior often leads to collisions, seriously threatening lives of peoples and property safety. Therefore, analyzing vehicle lane changing behavior is of great significance for reducing traffic accidents and improving driving efficiency [1-3].

The problem of vehicle lane changing has been widely studied. A brief review is presented in what follows.

At present, research on lane changing behavior of autonomous vehicles mainly focuses on vehicle motion status and lane changing trajectory prediction as well as minimum safety clearance, with less attention paid to safety and fairness issues during the lane changing process [4, 5]. Nilsson et al. identified lane changing intentions by calculating the lateral and longitudinal motion cues of vehicles and setting thresholds based on rules [6]. Chauhan et al. used the absolute value of cumulative lateral velocity to identify the time window of lane changing operations, and classified the lane changing behavior of vehicles [7]. Tran et al. discretized parameters such as vehicle speed, acceleration, and steering wheel angle, and inputted them into a hidden Markov model to identify driver lane changing strategies [8]. OH et al. established a binary logistic regression model to study driver lane changing behavior [9]. Shi et al. proposed a novel framework termed DeepAD for decision making [10]. Peng et al. proposed a Gaussian distribution based lane changing model for lane changing behavior on highways, which were used for lane changing trajectory planning. And also, a trajectory tracking control method based on adaptive cruise control for trajectory tracking was proposed, achieving good tracking results. However, the lateral velocity and acceleration of the trajectory obtained by this method were relatively high [11]. The method based on graph search has high randomness, is greatly affected by different environments, and has certain limitations for medium and high-speed working conditions. The collision risk based method mainly uses the artificial potential field method, but the path planned by this method has sudden changes in vehicle acceleration, which reduces passenger comfort. Since this method does not include vehicle dynamics, it cannot guarantee its application on actual vehicles [12]. With the rise of machine learning algorithms, most scholars have applied machine learning to lane changing path planning, among which the rule-based and machine learning fusion lane changing decision model is an important method [13]. Wang et al. used the obtained lane changing feasibility for long short-term memory neural networks, and finally predicted lane changing behavior [14]. Yao et al. constrained the longitudinal acceleration of the vehicle to improve safety under dangerous lane changing conditions [15]. This type of method research could effectively identify and predict the lane changing actions of vehicles, but it required a large amount of data sets for training. Dixit et al. proposed a new framework for achieving automatic overtaking in high-speed environments without making judgments on the safety of the opposite lane, reducing safety. Based on the collision time and distance between the vehicle and the connected vehicle, a lane changing control method for the driving safety boundary of the vehicle was designed which could simultaneously meet safety and comfort requirements [16]. Wang et al. proposed a model for dynamic traffic environments, taking into account the surrounding dynamic environment, to ensure that vehicles meet the requirements of safety, real-time performance during the lane changing process [17]. Fan et al. studied the problem of lane changing and obstacle avoidance from a safety perspective. To ensure the smooth process of lane changing, they studied the timing of lane changing and improved the stability of vehicles [18]. Wang et al. proposed a series of symplectic pseudospectral methods to solve nonlinear optimal control problems [19, 20]. Wang et al. proposed a unified symplectic pseudospectral method for motion planning and tracking control of 3D underactuated overhead cranes [21]. Liu et al. proposed the adaptive particle swarm optimization Gaussian pseudospectral method and the hp-adaptive Radau pseudospectral method for the optimal control problem of vehicle path tracking [22, 23].

The above research indicates that traditional rule-based lane changing driving strategies mostly characterize lane changing behavior by artificially defining vehicle operating state parameters, without in-depth analysis of the impact of each parameter on lane changing behavior, resulting in low accuracy of lane changing behavior recognition models, poor experience of lane changing driving strategies, and affecting driving safety. At present, driving technology neglects the driver’s factor. The methods for lane changing trajectory planning only consider lane changing behavior of a single driving style, without quantitatively considering the driving styles of drivers with different personality types based on the selection of evaluation indicators. This leads to poor driving fluency, affects the passenger experience, and brings discomfort. At the same time, most studies directly give the lane changing time and the driving state (position, velocity, acceleration) information of the self vehicle at the beginning and end of lane changing, and use a fifth degree polynomial to plan the lane changing trajectory, without considering the interaction effect between the self vehicle and surrounding vehicles.

2. Mathematical model of vehicle lane changing problem

2.1. Mathematical model of vehicle

A nonlinear 4-DOF vehicle model shown in Fig. 1 is used to describe the vehicle lane changing problem.

Fig. 14-DOF vehicle model

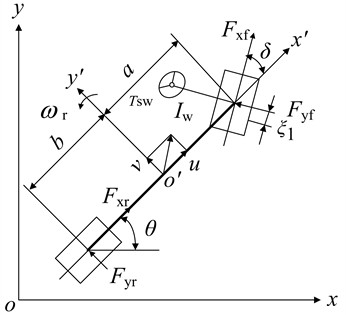
In state space form it is [1]:

1

\{\begin{array}{l} \dot{v} = - u ω + \frac{F_{y f} c o s δ + F_{y r} + F_{x f} s i n δ}{m}, \\ \dot{ω} = \frac{a F_{y f} c o s δ - b F_{y r} + a F_{x f} s i n δ}{I_{z}}, \\ \dot{u} = v ω + \frac{F_{x f} c o s δ - F_{y f} s i n δ + F_{x r} - F_{f} - F_{w}}{m}, \\ \dot{δ} = p, \\ \dot{p} = - \frac{k_{1} ξ_{1}}{I_{w} u} v - \frac{k_{1} ξ_{1} a}{I_{w} u} ω + \frac{(k_{1} ξ_{1} - k_{w})}{I_{w}} δ - \frac{c_{w}}{I_{w}} p + \frac{T_{s w} i}{I_{w}} . \end{array}

For the simplicity of applying optimal control methods and better verifying the effectiveness of the method through experiments, we select the state space as $x (t) = [u (t), v (t), ω (t), x (t), y (t)]^{T}$ and the control space as $z (t) = [δ]$ . The optimal control problem aims at finding a control input $z (t)$ and corresponding state variable $x (t)$ that minimize the cost function meanwhile satisfying the corresponding constraints. Then the Eq. (2) can be obtained by simplifying Eq. (1). The longitudinal and lateral speeds as well as the steering angle are the states that can be measured using sensors. The lateral distance and the yaw rate are different to be measured because of expensive sensors:

2

\dot{x} = f [x (t), z (t)] .

2.2. Optimal control object of path tracking problem

The minimum time required to complete the path tracking process is determined as the control object.

The cost function is:

3

J (z) = \int_{t_{0}}^{t_{f}} d t,

where $\{τ_{1}, τ_{2}, \dots, τ_{i}, \dots, τ_{N}\}$ , $(i = 1,2, \dots, N)$ is the initial time, $(- 1,1)$ is the final time.

2.3. Constrains

The initial and terminal states are described as:

4

x (t_{0}) = [u (t_{0}), 0,0, 0,0]^{T},

5

x (t_{f}) = [u (t_{f}), 0,0, x (t_{f}), y (t_{f})]^{T} .

When the braking maneuver is applied to decelerate the vehicle, the constraints on $F_{x f}$ , $F_{x r}$ can be rewritten in the following manner:

6

\{\begin{array}{l} F_{x f} \geq - \frac{μ m g (b + μ h_{g})}{a + b}, \\ F_{x r} = \frac{a - μ h_{g}}{b + μ h_{g}} F_{x f} . \end{array}

So the optimal path tracking problem can be described as:

7

m i n J; s . t . \dot{x} = f [x (t), u (t), t], h \leq 0,

where $h$ expresses the inequality constraint.

3. hp adaptive pseudospectral method for solving optimal trajectory

The traditional global pseudospectral method has the advantages of simplicity and efficiency, but its performance is not ideal when solving large, complex, and nonsmooth problems. As the number of discrete points increases, it becomes increasingly complex when transformed into corresponding nonlinear programming problems. Because the corresponding control variables may not be continuous when there are different path constraints. The idea of segmented optimization can be introduced into the pseudospectral method to improve performance of algorithm. The only difference is that the hp adaptive pseudospectral method adds a new error evaluation criterion. Its function is to more reasonably adjust the segmentation of the entire trajectory optimization time period and adjust the number of discretization points, avoiding the need to repeatedly densify the grid to improve accuracy. At the same time, it can obtain a sparse differential equation matrix, effectively reducing the NLP scale and improving convergence speed while reducing initial sensitivity. Let $e$ be the maximum allowable error for discretized dynamic constraints and path constraints. If the allowable error for a certain discrete interval is higher than $e$ , adaptive adjustments are made to the interval mesh density $h$ and the order $p$ of the global interpolation polynomial.

3.1. Discretization of continuous optimal control problem

The discretization process of Gauss pseudospectral method for optimizing the problem of vehicle lane changing is as follows.

The time interval $[t_{0}, t_{f}]$ of the optimal control problem is divided into $K$ grids and is converted into intervals $[- 1,1]$ :

8

t = \frac{t_{k} - t_{k - 1}}{2} τ + \frac{t_{k} + t_{k - 1}}{2}, t_{k} > t_{k - 1},

where $t \in [t_{k - 1}, t_{k}]$ ; $τ \in [- 1,1]$ ; $k = 1,2, \dots, K$ ; $t_{0} \leq \dots \leq t_{K} = t_{f}$ .

The LG collocation points of $\{τ_{1}, τ_{2}, \dots, τ_{i}, \dots, τ_{N}\}$ $(i = 1,2, \dots, N)$ in interval of $(- 1,1)$ are the zeros of the N-order Legendre polynomial:

9

G_{N} (τ) = \frac{1}{2^{N} N!} \cdot \frac{d^{N}}{d τ^{N}} [(τ^{2} - 1)^{N}] .

Due to the fact that the research object involves both initial and terminal constraints, it is necessary to introduce two nodes: the initial and terminal time. The state variables at the first $N + 1$ LG collocation points are discretized. The state variables are approximated using the $N + 1$ order Lagrange interpolation polynomial as the basis function:

10

\{\begin{array}{l} x^{(k)} (τ) \approx X^{(k)} (τ) = \sum_{j = 0}^{N} X_{j}^{(k)} (τ) L_{j}^{(k)} (τ), \\ L_{j}^{(k)} (τ) = \prod_{\begin{array}{l} l = 0 \\ l \neq j \end{array}}^{N} \frac{τ - τ_{l}^{(k)}}{τ_{j} - τ_{l}^{(k)}}, j = 0,1, \dots, N . \end{array}

Similarly, the control variables are discretized at $N$ LG collocations. Eq. (11) can be approximated using $N$ -order Lagrange interpolation polynomials:

11

\{\begin{array}{l} u^{(k)} (τ) \approx U^{(k)} (τ) = \sum_{j = 1}^{N} U_{j}^{(k)} (τ) {\tilde{L}}_{j}^{(k)} (τ), \\ {\tilde{L}}_{j}^{(k)} (τ) = \prod_{\begin{array}{l} l = 1 \\ l \neq j \end{array}}^{N} \frac{τ - τ_{l}^{(k)}}{τ_{j} - τ_{l}^{(k)}}, j = 1,2, \dots, N . \end{array}

Eq. (10) does not define the terminal time state, and the initial time is known. So Eq. (12) can be approximated by discretization through integral operations:

12

x (τ_{f}) \approx X (τ_{f}) = X (τ_{0}) + \frac{t_{k} - t_{k - 1}}{2} \sum_{k = 1}^{K} \sum_{i = 1}^{N} ω_{i}^{(k)} \times f [X^{(k)} (τ_{i}), U^{(k)} (τ_{i}), τ; t_{k - 1}, t_{k}],

where $τ_{i} (i = 1,2, \dots, N)$ is the LG point; $ω_{i}^{(k)}$ is the Gaussian weight factor.

The time derivative of the state variable is approximated as:

13

\{\begin{array}{l} \sum_{j = 0}^{N} {\dot{L}}_{j}^{(k)} (τ_{i}) x_{j}^{(k)} (τ_{i}) = \frac{t_{k} - t_{k - 1}}{2} V^{(k)} (τ_{i}) c o s γ^{(k)} (τ_{i}), \\ \sum_{j = 0}^{N} {\dot{L}}_{j}^{(k)} (τ_{i}) h_{j}^{(k)} (τ_{i}) = \frac{t_{k} - t_{k - 1}}{2} V^{(k)} (τ_{i}) s i n γ^{(k)} (τ_{i}), \\ \sum_{j = 0}^{N} {\dot{L}}_{j}^{(k)} (τ_{i}) V_{j}^{(k)} (τ_{i}) = \frac{t_{k} - t_{k - 1}}{2} \times (\frac{T^{(k)} (τ_{i}) c o s α^{(k)} (τ_{i}) - D^{(k)} (τ_{i})}{m} - g s i n γ^{(k)} (τ_{i})), \\ \sum_{j = 0}^{N} {\dot{L}}_{j}^{(k)} (τ_{i}) γ_{j}^{(k)} (τ_{i}) = \frac{t_{k} - t_{k - 1}}{2} (\begin{matrix} \frac{T^{(k)} (τ_{i}) s i n α^{(k)} (τ_{i})}{m g} \\ + \frac{L^{(k)} (τ_{i})}{m g} - c o s γ^{(k)} (τ_{i}) \end{matrix}) \frac{g}{V^{(k)} (τ_{i})}, \\ \sum_{j = 0}^{N} {\dot{L}}_{j}^{(k)} (τ_{i}) m_{j}^{(k)} (τ_{i}) = - \frac{t_{k} - t_{k - 1}}{2} \times s_{f c}^{(k)} (τ_{i}) T^{(k)} (τ_{i}) / 3600 . \end{array}

Eq. (14) can be obtained by discretizing the real-time path constraints:

14

C [X^{(k)} (τ_{i}), U^{(k)} (τ_{i}), τ; t_{k - 1}, t_{k}] ⩽ 0 .

Eq. (15) can be obtained by discretizing the objective function and solving the integration term using numerical integration:

15

J = Φ (X (τ_{0}), t_{0}, X (τ_{f}), t_{f}) + \frac{t_{k} - t_{k - 1}}{2} \times \sum_{k = 1}^{K} \sum_{i = 1}^{N} ω_{i}^{k} L [X^{(k)} (τ_{i}), U^{(k)} (τ_{i}), τ, t_{k - 1}, t_{k}] .

3.2. Adaptive judgment criteria

In order to determine whether the grid should be refined or whether the degree of approximation polynomial should be increased, the curvature $κ^{(k)} (τ_{i})$ of the approximate value $X^{(k)} (τ_{i})$ of the $i$ th state component in the $k$ th grid interval needs to be calculated as:

16

κ^{(k)} (τ) = \frac{|{\ddot{X}}^{(k)} (τ_{i})|}{|{[1 + {\dot{X}}^{(k)} {(τ_{i})}^{2}]}^{\frac{3}{2}}|} .

The ratio of maximum curvature $κ_{m a x}^{(k)}$ to average curvature ${\bar{κ}}^{(k)}$ is defined as:

17

r_{k} = \frac{κ_{m a x}^{(k)}}{{\bar{κ}}^{(k)}} .

If $r_{k} > {r_{k}}_{m a x}$ there is a large curvature between the grid intervals compared to the other grid intervals. And the grid should be refined and the number of collocations should be increased. If $r_{k} < {r_{k}}_{m a x}$ , the order of the polynomial should be increased to achieve better approximation on the grid interval.

3.3. Calculation of the adaptive update variable

The order $N_{k}$ of the polynomial in the $k$ th grid interval after updating is determined by Eq. (18):

18

N_{k} = M_{d} + c e i l [l g (e_{m a x}^{(k)} / e)] + A_{d},

where $M_{d}$ is the initial order of the polynomial in the grid; $A_{d} > 0$ is the integer constant that controls the increase of the number of collocations in the grid; $e_{m a x}^{(k)}$ is the maximum error; $c e i l (\cdot)$ is the operator that rounds to the next highest integer.

The new number of grid intervals $n_{k}$ for the updated entire trajectory is determined by the following equation:

19

n_{k} = c e i l [c_{e} l g (e_{m a x}^{(k)} / e)],

where $c_{e}$ is an integer constant that controls the increase of the number of grid intervals. The density function can be expressed by using the integration of curvature density function to determine the position of new grid points as:

20

p (τ) = c_{τ} κ (τ)^{\frac{1}{3}} .

The constant parameter $c_{τ}$ satisfies:

21

\int_{- 1}^{1} p (ζ) d ζ = 1 .

The cumulative distribution function is:

22

F (τ) = \int_{- 1}^{τ} p (ζ) d ζ .

The positions of $n_{k}$ points in the corresponding next iteration can be determined by the following equation:

23

F (τ_{i}) = \frac{i - 1}{n_{k}}, 1 \leq i \leq n_{k} + 1 .

If $n_{k} =$ 1, no new sub intervals will be created. The minimum value of $n_{k}$ is at least 2.

3.4. Algorithm process

The process of the hp adaptive pseudospectral algorithm is as follows:

1) Forming an initialization grid.

2) For each grid $k = 1,2, \dots, K$ a fixed order approximate polynomial is used to solve the NLP problem.

3) If $e_{m a x}^{(k)} \leq e$ , the next grid $k$ is proceed.

4) If $r_{k} \geq r_{k m a x}$ or $N_{k} > M_{d}$ , the $k$ th grid interval is refined to $n_{k}$ sub intervals. And then the order of the polynomial of any sub interval is set to $M_{d}$ . Then the next grid $k$ is proceed.

5) Otherwise, the order of the $k$ th sub interval of the polynomial is set to $N k$ .

6) After updating the grid parameters, returning to step 2) and procing to the next iteration.

4. Numerical simulations and experimental verification

4.1. Numerical simulations

This section uses the automotive dynamics simulation software CarSim to verify the feasibility and effectiveness of the control strategy of shortest time lane changing.

Fig. 2 is the simulation result under the condition of emergency collision avoidance.

Fig. 2Simulation result the condition of emergency collision avoidance

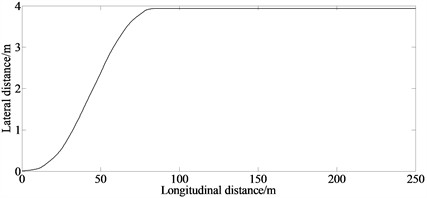
a) Lateral distance

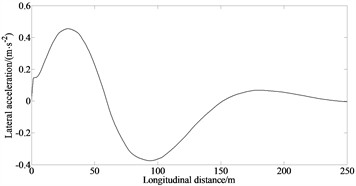
b) Lateral acceleration

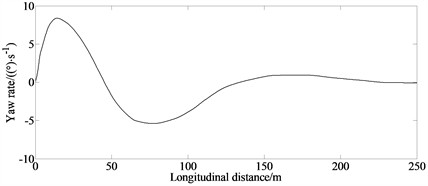
c) Yaw rate

Fig. 2(a) indicates that the vehicle successfully completes lane changing maneuvers with shorted time. The vehicle did not collide during the lane change process, and both the state and control variables meet the constraint conditions. The hp adaptive pseudospectral method requires that the state variables remain continuous in the time domain and at the connection points between adjacent time domains, thus meeting the constraints of vehicle motion characteristics. Figs. 2(b)-(c) indicates that with the control of the proposed algorithm it can control the vehicle accurately during lane changing process, greatly improving the safety during lane changing and the ability of the vehicle to avoid collocation. This is because the hp adaptive pseudospectral method combines the advantages of local and global collocation methods. It adjusts the time segmentation and polynomial order according to the calculation accuracy requirements, thereby improving the calculation accuracy indicating that the hp adaptive pseudospectral method is suitable for solving optimal control problems with complex changes in state variables. The proposed method provides important technical support for the design of unmanned intelligent vehicles especially in the vehicle safety design in more complex traffic situations, and also provides new ideas for trajectory planning research of unmanned intelligent vehicles in practical engineering fields. Additionally, a driver assistance system that can provide practical guidance for lane-changing handling inputs can be constructed.

Fig. 3 is the simulation result under general collision avoidance condition.

Fig. 3(a) indicates that the designed lane change control method can effectively manipulate the vehicle to complete the lane changing process and meet safety requirements while satisfying various constraints. The optimization time is short and the real-time performance is better. Fig. 3(b) indicates that compared with emergency collision avoidance condition, the lateral acceleration is smaller. This is because under the general collision avoidance condition the driver has enough time to manipulate the vehicle to complete the lane changing process. From Fig. 3(c) it can be seen that there is sufficient distance during the lane change process to ensure the safety of the lane change of the vehicle while keeping the overall risk level of the system at a low level.

Fig. 3Simulation result under general avoidance condition

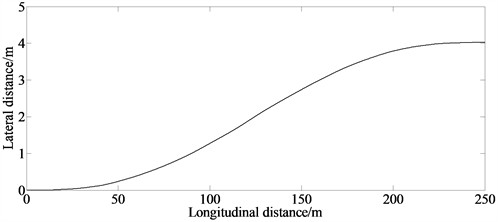
a) Lateral distance

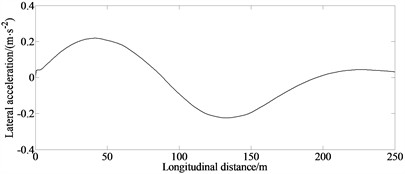
b) Lateral acceleration

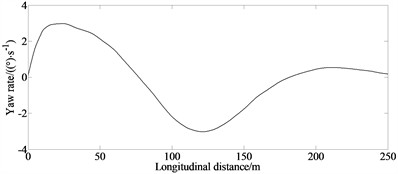
c) Yaw rate

4.2. Efficiency verification

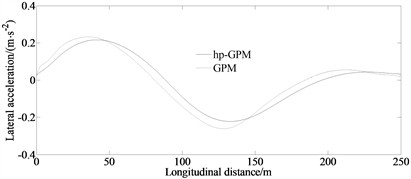
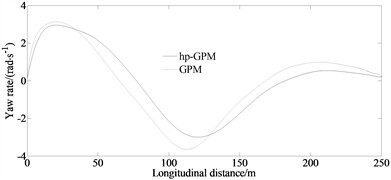
By comparing simulation, it can be seen that using the hp Gaussian pseudospectral method has better advantages than traditional optimization algorithms under the same initial values and constraints. And also, compared with Gaussian pseudospectral optimization, the proposed algorithm reduces the optimization dimension and avoids the significant influence of initial values on Gaussian pseudospectral optimization.

Fig. 4Comparison results between hp-GPM and GPM

4.3. Controller robustness verification in external disturbance environment

There is external interference in the process of lane changing with high speed for a vehicle. So it is necessary to verify the control effect of the hp-GPM. The maximum speed of wind is set as 50 km/h. The step gust is shown in Fig. 5.

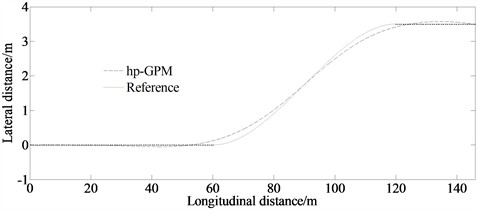
Fig. 6 shows the lane changing effect when the vehicle is disturbed by lateral wind. It can be seen from Fig. 6 that the proposed method can control the vehicle to complete the process of lane changing well according to the ideal reference even there is lateral wind interference.

Fig. 5Step gust

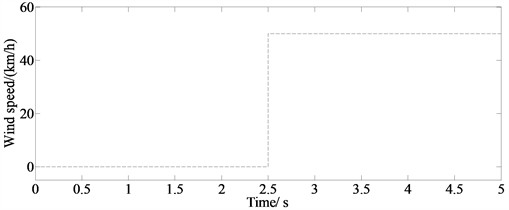
Fig. 6Lateral distance in external disturbance environment

4.4. Experimental verification

A virtual test adopting the Carsim software is conducted to verify the feasibility of the simulated results.

CarSim is a simulation software specifically developed for vehicle dynamics, which enjoys a high reputation internationally and is adopted by numerous automobile manufacturers and component suppliers. The main user interface of CarSim software consists of two modules: graphical user interface (SGUI) and graphical data management system. Its model runs 3-6 times faster on the computer than real-time operation. In the database, parameters such as road environment information, driver model, vehicle model, and aerodynamic response can be set. The CarSim simulation platform has the advantages of accuracy, convenience, good visualization, high cost-effectiveness and real-time monitoring and has good practicality for this study. CarSim is simulation software developed by Mechanical Simulation Corporation to simulate vehicle driving behavior. It has the functions of vehicle dynamics simulation and 3D animation demonstration, mainly used to predict and simulate the handling stability, braking performance, smoothness, power performance, and economy of tractors, sedans, and trucks. Its graphical interface is user-friendly and allows for the output of simulation results for user-defined variables. CarSim not only offers a wide range of vehicle models for users to choose from, but the 3D Surface module can also model road environments and scenes according to user needs. The Plot module can select simulation output parameters such as real-time vehicle position, speed, steering angle, vertical force, etc. So that users can analyze vehicle motion during the simulation process. Video+Plot also provides 3D simulation animations and allows users to customize variable changes during vehicle driving.

In order to further verify the superiority of the proposed algorithm of vehicle lane changing, this paper conducted real vehicle test verification. The real test vehicle is shown in Fig. 7. The measurement equipments are shown in Fig. 8.

From the Fig. 9(a) it can be seen that there is a significant lateral deviation when the vehicle is turning, and when driving on a straight road, the lateral deviation is relatively small due to the small steering angle. From the Fig. 9(b) it can be seen that the algorithm proposed in this paper can meet the constraints and effectively perform tracking control of lane changing. However, due to neglecting factors such as tire dynamics modeling, tire force coordinate transformation, and vehicle dynamics coupling, the model cannot accurately describe the dynamic characteristics of lateral collision avoidance process of the vehicle, resulting in calculation errors. Another reason for the certain error between simulation values and experimental values is that each driver’s subjective feelings and driving skills are different during the experiment, resulting in different reactions from each driver.

Fig. 7Real test vehicle

a)

b)

Fig. 8Measurement equipment’s

a)

b)

Fig. 9Experimental results of lateral acceleration and lateral distance

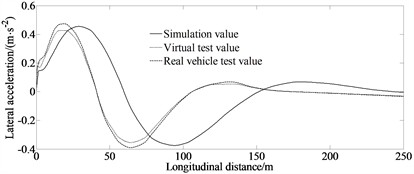
a) Lateral acceleration

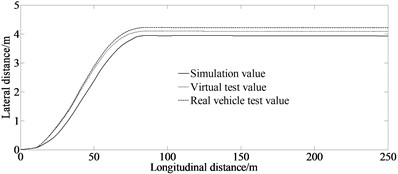
b) Lateral distance

Table 1Comparison of mean values of absolute error between different methods

	Mean value of absolute error
Lateral distance (m)	0.1827
Lateral acceleration (m⋅s²)	0.6500

5. Conclusions

To solve the problem of optimal lane changing, firstly, a nonlinear 4-DOF vehicle model is established to describe the vehicle lane changing problem. Based on the model, various constraints are considered to construct an optimization problem with constraints. Subsequently, the hp Gaussian pseudospectral method is used to discretize the continuous optimization problem into a constrained nonlinear programming problem. Then, the sequence quadratic program method is used to solve the time optimal trajectory. Finally, the effectiveness of the proposed method is verified through experiments. The results indicate that the proposed method can accurately control the vehicle to change lanes along a given trajectory in the shortest time while satisfying the constraints.

The optimization method proposed in this article is based on the absence of interfering vehicles in adjacent lanes, and there is no analysis of the optimal lane change control under different operating conditions for multiple vehicles. In the future, more in-depth research can be conducted in this area to improve and perfect lane change of emergency avoidance methods. At the same time, the next step of research will optimize the computational efficiency of the hp adaptive pseudospectral method, and build hardware in the loop and real vehicle testing environments to further verify the feasibility and effectiveness of the proposed optimal lane changing tracking control strategy. In the future, statistical analyses and the significance tests should be researched to enhance the credibility of the findings and validate the reliability of the results. At the same time, although the hp adaptive pseudospectral method has a fast convergence speed, due to the transformation of continuous time optimization problems into high-dimensional nonlinear programming problems, poor initial value guessing can lead to slow convergence or even iteration failure in the solution process for high-dimensional nonlinear programming problems. Therefore, in the future, in order to improve the solving efficiency of the hp adaptive pseudospectral method while ensuring its high-precision solution, it is necessary to study methods for quickly obtaining near optimal initial solutions.

References

Y. Liu, D. Cui, and W. Peng, “Optimum control for path tracking problem of vehicle handling inverse dynamics,” Sensors, Vol. 23, No. 15, p. 6673, Jul. 2023, https://doi.org/10.3390/s23156673

Publisher
Y. Liu, D. Cui, and W. Peng, “Optimal lane changing problem of vehicle handling inverse dynamics based on mesh refinement method,” IEEE Access, Vol. 11, pp. 115617–115626, Jan. 2023, https://doi.org/10.1109/access.2023.3324422

Publisher
Y. Liu and D. Cui, “Vehicle dynamics prediction via adaptive robust unscented particle filter,” Advances in Mechanical Engineering, Vol. 15, No. 5, p. 168781322311707, May 2023, https://doi.org/10.1177/16878132231170766

Publisher
Y. Ali, Z. Zheng, M. M. Haque, and M. Wang, “A game theory-based approach for modelling mandatory lane-changing behaviour in a connected environment,” Transportation Research Part C: Emerging Technologies, Vol. 106, pp. 220–242, Sep. 2019, https://doi.org/10.1016/j.trc.2019.07.011

Publisher
P. Hang, C. Lv, C. Huang, J. Cai, Z. Hu, and Y. Xing, “An integrated framework of decision making and motion planning for autonomous vehicles considering social behaviors,” IEEE Transactions on Vehicular Technology, Vol. 69, No. 12, pp. 14458–14469, Dec. 2020, https://doi.org/10.1109/tvt.2020.3040398

Publisher
J. Nilsson, J. Fredriksson, and E. Coelingh, “Rule-based highway maneuver intention recognition,” in IEEE 18th International Conference on Intelligent Transportation Systems – (ITSC 2015), pp. 950–955, Sep. 2015, https://doi.org/10.1109/itsc.2015.159

Publisher
P. Chauhan, V. Kanagaraj, and G. Asaithambi, “Understanding the mechanism of lane changing process and dynamics using microscopic traffic data,” Physica A: Statistical Mechanics and its Applications, Vol. 593, p. 126981, May 2022, https://doi.org/10.1016/j.physa.2022.126981

Publisher
D. Tran, J. Du, W. Sheng, D. Osipychev, Y. Sun, and H. Bai, “A human-vehicle collaborative driving framework for driver assistance,” IEEE Transactions on Intelligent Transportation Systems, Vol. 20, No. 9, pp. 3470–3485, Sep. 2019, https://doi.org/10.1109/tits.2018.2878027

Publisher
C. Oh, J. Choi, and S. Park, “In-depth understanding of lane changing interactions for in-vehicle driving assistance systems,” International Journal of Automotive Technology, Vol. 18, No. 2, pp. 357–363, Jan. 2017, https://doi.org/10.1007/s12239-017-0036-2

Publisher
Y. Shi, J. Liu, C. Liu, and Z. Gu, “DeepAD: An integrated decision-making framework for intelligent autonomous driving,” Transportation Research Part A: Policy and Practice, Vol. 183, p. 104069, May 2024, https://doi.org/10.1016/j.tra.2024.104069

Publisher
T. Peng et al., “A new safe lane-change trajectory model and collision avoidance control method for automatic driving vehicles,” Expert Systems with Applications, Vol. 141, p. 112953, Mar. 2020, https://doi.org/10.1016/j.eswa.2019.112953

Publisher
D.-S. Pae, G.-H. Kim, T.-K. Kang, and M.-T. Lim, “Path planning based on obstacle-dependent gaussian model predictive control for autonomous driving,” Applied Sciences, Vol. 11, No. 8, p. 3703, Apr. 2021, https://doi.org/10.3390/app11083703

Publisher
H. Jia, P. Liu, L. Zhang, and Z. Wang, “Lane-changing decision model development by combining rules abstract and machine learning technique,” Journal of Mechanical Engineering, Vol. 58, No. 4, p. 212, Jan. 2022, https://doi.org/10.3901/jme.2022.04.212

Publisher
W. Wang, T. Qie, C. Yang, W. Liu, C. Xiang, and K. Huang, “An intelligent lane-changing behavior prediction and decision-making strategy for an autonomous vehicle,” IEEE Transactions on Industrial Electronics, Vol. 69, No. 3, pp. 2927–2937, Mar. 2022, https://doi.org/10.1109/tie.2021.3066943

Publisher
J. Yao, G. Chen, and Z. Gao, “Target vehicle selection algorithm for adaptive cruise control based on lane-changing intention of preceding vehicle,” Chinese Journal of Mechanical Engineering, Vol. 34, No. 1, pp. 406–423, Dec. 2021, https://doi.org/10.1186/s10033-021-00650-8

Publisher
S. Dixit et al., “Trajectory planning for autonomous high-speed overtaking in structured environments using robust MPC,” IEEE Transactions on Intelligent Transportation Systems, Vol. 21, No. 6, pp. 2310–2323, Jun. 2020, https://doi.org/10.1109/tits.2019.2916354

Publisher
Y. Wang, C. Wei, and L. Ma, “Dynamic lane-changing trajectory planning model for intelligent vehicle based on quadratic programming,” China Journal of Highway and Transport, Vol. 34, No. 7, pp. 79–94, 2021, https://doi.org/1001-7372(2021)07-0079-16

Search CrossRef
J. Fan, J. Liang, and A. K. Tula, “A lane changing time point and path tracking framework for autonomous ground vehicle,” IET Intelligent Transport Systems, Vol. 16, No. 7, pp. 860–874, Mar. 2022, https://doi.org/10.1049/itr2.12180

Publisher
X. Wang, J. Liu, H. Peng, and X. Zhao, “An iterative framework to solve nonlinear optimal control with proportional delay using successive convexification and symplectic multi-interval pseudospectral scheme,” Applied Mathematics and Computation, Vol. 435, p. 127448, Dec. 2022, https://doi.org/10.1016/j.amc.2022.127448

Publisher
X. Wang, H. Peng, S. Zhang, B. Chen, and W. Zhong, “A symplectic pseudospectral method for nonlinear optimal control problems with inequality constraints,” ISA Transactions, Vol. 68, pp. 335–352, May 2017, https://doi.org/10.1016/j.isatra.2017.02.018

Publisher
X. Wang, J. Liu, Y. Zhang, B. Shi, D. Jiang, and H. Peng, “A unified symplectic pseudospectral method for motion planning and tracking control of 3D underactuated overhead cranes,” International Journal of Robust and Nonlinear Control, Vol. 29, No. 7, pp. 2236–2253, May 2019, https://doi.org/10.1002/rnc.4488

Publisher
Y. Liu and D. Cui, “Optimal control of vehicle path tracking problem,” World Electric Vehicle Journal, Vol. 15, No. 9, p. 429, Sep. 2024, https://doi.org/10.3390/wevj15090429

Publisher
Y. Liu and D. Cui, “Optimal control problem path tracking of an intelligent vehicle,” World Electric Vehicle Journal, Vol. 15, No. 9, p. 428, Sep. 2024, https://doi.org/10.3390/wevj15090428

Publisher

About this article

Received

18 August 2024

Accepted

17 December 2024

Published

18 January 2025

SUBJECTS

Vibration in transportation engineering

DOI

https://doi.org/10.21595/jve.2024.24462

Keywords

vehicle dynamics

lane changing

optimal control

HP adaptive pseudo-spectral method

Acknowledgements

This research was supported by the Open Research Program of Huzhou Key Laboratory of Urban Multidimensional Perception and Intelligent Computing under Grant No. UMPIC202404. The authors gratefully acknowledge the support agency.

Data Availability

The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

Author Contributions

Yingjie Liu: mathematical model and the simulation techniques. Dawei Cui: spelling and grammar checking as well as virtual validation

Conflict of interest

The authors declare that they have no conflict of interest.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Research article

2024 02 18

Optimal control of autonomous vehicle path tracking based on whale optimization algorithm

Fang Han, Yingjie Liu, Wen Peng

Research article

2023 08 01

Minimum-time lane changing problem of vehicle handling inverse dynamics based on adaptive mesh refinement and collocation optimization method

Yingjie Liu, Dawei Cui, Wen Peng

Research article

2019 12 31

Path tracking with minimum time of vehicle handling inverse dynamics based on adaptive gauss pseudospectral method

Yongsheng Liu, Yingjie Liu

Research article

2019 08 15

Multi-objective optimization of active suspension predictive control based on improved PSO algorithm

Qiang Zhao, Baoquan Zhu

Y. Liu, D. Cui, and C. Xie, “Optimal control of lane changing problem of intelligent vehicle,” Journal of Vibroengineering, Vol. 27, No. 1, –13, Jan. 2025, https://doi.org/10.21595/jve.2024.24462

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jve.2024.24462
UR  - https://doi.org/10.21595/jve.2024.24462
TI  - Optimal control of lane changing problem of intelligent vehicle
T2  - Journal of Vibroengineering
AU  - Liu, Yingjie
AU  - Cui, Dawei
AU  - Xie, Chenglian
PY  - 2025
DA  - 2025/01/18
PB  - Extrica
VL  - 27
IS  - 1
SN  - 1392-8716
SN  - 2538-8460
ER  - 

Copy Ris

Copied to clipboard!

 @article{Liu_2025, title={Optimal control of lane changing problem of intelligent vehicle}, ISSN={2538-8460}, url={https://doi.org/10.21595/jve.2024.24462}, DOI={10.21595/jve.2024.24462}, journal={Journal of Vibroengineering}, publisher={JVE International Ltd.}, author={Liu, Yingjie and Cui, Dawei and Xie, Chenglian}, year={2025}, month=jan }

Copy Bibtex

Copied to clipboard!

[1]Y. Liu, D. Cui, and C. Xie, “Optimal control of lane changing problem of intelligent vehicle,” Journal of Vibroengineering, Jan. 2025, doi: 10.21595/jve.2024.24462.

Copy IEEE

Copied to clipboard!

Liu, Yingjie, Dawei Cui, and Chenglian Xie. “Optimal Control of Lane Changing Problem of Intelligent Vehicle.” Journal of Vibroengineering, January 18, 2025. https://doi.org/10.21595/jve.2024.24462.

Copy Chicago

Copied to clipboard!

Optimal control of lane changing problem of intelligent vehicle

Abstract

Highlights

1. Introduction

2. Mathematical model of vehicle lane changing problem

2.1. Mathematical model of vehicle

2.2. Optimal control object of path tracking problem

2.3. Constrains

3. hp adaptive pseudospectral method for solving optimal trajectory

3.1. Discretization of continuous optimal control problem

3.2. Adaptive judgment criteria

3.3. Calculation of the adaptive update variable

3.4. Algorithm process

4. Numerical simulations and experimental verification

4.1. Numerical simulations

4.2. Efficiency verification

4.3. Controller robustness verification in external disturbance environment

4.4. Experimental verification

5. Conclusions

References

About this article

Related Articles