Multi-scale optimization design of viscoelastic damping sandwich plate

Fang, Zhanpeng; An, Haoping; Xiao, Yanqiu

doi:10.21595/jve.2025.24360

Journal of Vibroengineering

Browse Journal

Submit article

Published: 22 January 2025

Check for updates

Multi-scale optimization design of viscoelastic damping sandwich plate

Zhanpeng Fang¹

Haoping An²

Yanqiu Xiao³

^{1, 3}Collaborative Innovation Center of Intelligent Tunnel Boring Machine, Zhengzhou University of Light Industry, Henan Province, Zhengzhou, 450003, China

²Henan Academy of Sciences Institute of Applied Physics Co., Ltd., Zhengzhou, 450008, China

Corresponding Author:

Haoping An

Cite the article Download PDF

Article in Press

Downloads 16

Abstract

Aiming at the optimization design problem of viscoelastic damping sandwich plate under the background of lightweight, a multi-scale optimization design method is proposed to realize the collaborative optimization design of viscoelastic damping sandwich plate in both macro and micro scales. It is assumed that the viscoelastic damping material is microscopically composed of 3D periodic unit cells. The effective constitutive matrix of the unit cell is derived using the homogenization method. The topology optimization model is established, and sensitivity analysis is conducted. The iteration of the design variables is realized by the Optimization Criterion (OC) method. Several numerical examples are presented to demonstrate the effectiveness of the proposed multi-scale optimization method. In-depth discussions are given for the impact of optimization objectives and volume fractions on the design results. The results show that the optimized configuration on both scales are dependent on the objective mode. The macroscopic optimal layout is affected by the microscopic volume fraction, while the change in macroscopic volume fraction has little effect on the microscopic optimal configuration. The dynamic characteristics of the viscoelastic damping sandwich plate are improved significantly through multi-scale optimization design.

1. Introduction

Viscoelastic damping materials are commonly used to reduce vibration and noise radiation in plate and shell structures, and viscoelastic damping sandwich panels have been widely used in automotive, aviation, and aerospace industries due to their simple structure, low cost and high damping [1]. To design lightweight structures with high damping characteristics, the layout of viscoelastic damping materials needs to be optimized.

Topology optimization provides a powerful solution for vibration and noise reduction design of viscoelastic damping sandwich panels in the context of lightweight. This technique optimizes the topological configuration of the viscoelastic damping layer over the entire design region at the macro-scale, in order to improve the structural modal loss factor [2-5], suppress the structural vibration response [6-8] and reduce the noise radiation from the structure [9-10].

Multi-objective optimization of viscoelastic damping sandwich plates is performed to simultaneously minimize the weight and maximize the modal loss factor of viscoelastic damping sandwich plates [11-12]. The ability of viscoelastic damping sandwich panels to dissipate vibration energy is affected by the properties of the viscoelastic damping material, and thus, the micro topological configuration of the viscoelastic damping material is optimized to obtain the best viscoelastic damping material properties [13-14] or to improve the macrostructural vibration characteristics [15-17].

The aforementioned works on topology optimization of viscoelastic damping materials have focused on either macro- or micro-structure. At the macroscale, structures with excellent performance are obtained by optimizing the topological configurations of the macrostructure. At the microscale, the properties of materials are improved by changing the micro topological configuration. Multi-scale optimization design of viscoelastic damping sandwich panels can lead to better design results in terms of damping performance. Zhang et al. [18] proposed a multi-scale topology optimization method based on the maximization of modal loss factor, which is applicable to viscoelastic damping plate, and optimizes both the macroscopic layout and microscopic configuration of viscoelastic damping materials, which significantly improves the dynamic performance of viscoelastic damping plate. This study is aimed at the free damping structure, whose micro-cells are two-dimensional structures, and the influence of macroeigenvectors is ignored in the sensitivity analysis.

Different from the energy dissipation principle of free damping structure, the vibration energy of viscoelastic damping sandwich plate is dissipated mainly through the shear strain of the viscoelastic damping layer. and thus, microscopically, the micro-cell of viscoelastic damping layer is a three-dimensional structure in order to obtain the three equivalent shear moduli. A multi-scale topology optimization model for viscoelastic damping sandwich plates is established. The sensitivity of the optimization target with respect to macro and micro design variables is derived and the influence of macro eigenvectors on the sensitivity of the optimization target with respect to the macro design variables is considered. The optimization criterion method is used to update the macroscopic and microscopic design variables at the same time, and the macroscopic and microscopic optimized configurations of the viscoelastic damping sandwich plate are finally obtained.

2. Multi-scale viscoelastic damping sandwich plate and its damping property

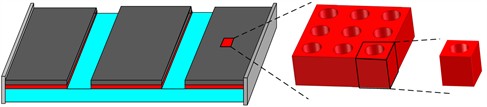
To realize the multi-scale topology optimization design of the viscoelastic damping sandwich plate, it is first necessary to establish the dynamics model of the multi-scale viscoelastic damping sandwich plate. Fig. 1 shows the schematic diagram of the multi-scale viscoelastic damping sandwich plate. Fig. 1(a) shows the macrostructure of a viscoelastic damping sandwich plate with a viscoelastic damping layer consisting of a periodic damping material (as shown in Fig. 1(b)) and microstructure in Fig. 1(c).

Fig. 1Schematic diagram of the multi-scale viscoelastic damping sandwich plate: macrostructure, periodic damping material and microstructure

Schematic diagram of the multi-scale viscoelastic damping sandwich plate: macrostructure, periodic damping material and microstructure

2.1. Homogenization analysis of viscoelastic damping layer

The viscoelastic damping layer is composed of three-dimensional unit cells, and homogenization analysis of the unit cell leads to an equivalent elastic matrix containing the equivalent transverse shear elastic moduli. Finite element model of the unit cell is carried out using eight-node hexahedron element. During the finite element analysis of the unit cell, the finite element equilibrium equation under periodic boundary conditions, is given by Eq. (1):

1

k u = f^{M I},

where $u$ is the displacement field. $k$ is the stiffness matrix of the unit cell, which can be expressed as Eq. (2):

2

k = \sum_{j = 1}^{n} k_{j} = \sum_{j = 1}^{n} \int_{Y_{j}} b^{T} D_{j}^{M I} b d Y_{j},

where $k_{j}$ and $D_{j}^{M I}$ are the stiffness and elasticity matrices of the $j$ -th element in the microstructure, respectively; $Y_{j}$ is the volume of the $j$ -th element; $b$ is the strain matrix and $n$ is the total number of elements in the microstructure of the viscoelastic damping layer.

$f^{M I}$ in Eq. (1) is the load vector caused by uniform strain fields, which can be expressed as Eq. (3):

3

f^{M I} = \sum_{j = 1}^{n} f_{j}^{M I} = \sum_{j = 1}^{n} \int_{Y_{j}} b^{T} D_{j}^{M I} d Y_{j},

where $f_{j}^{M I}$ is the load matrix of the $j$ -th element.

Based on the homogenization method, the homogenized elasticity matrix of the viscoelastic damping layer $D^{H}$ can be expressed Eq. (4):

4

D^{H} = \frac{1}{|Y|} \sum_{j = 1}^{n} \int_{Y_{j}} D_{j}^{M I} (I - b u_{j}) d Y_{j},

where $|Y|$ is the volume of the unit cell; $I$ is the unit matrix, and $u_{j}$ is the displacement matrix of the $j$ -th element.

The average density of the unit cell can be calculated by Eq. (5):

5

ρ^{H} = \frac{\sum_{j = 1}^{n} ρ_{j}^{v}}{n},

where $ρ_{j}^{v}$ is the density of the $j$ -th element.

2.2. Damping property of viscoelastic damping sandwich plate

The complex elastic matrix of viscoelastic damping material can be expressed as Eq. (6):

6

D^{v} = {D^{v}}^{'} + i D^{v^{''}} = {D^{v}}^{'} (1 + i η),

where ${D^{v}}^{'}$ is the real part of the complex elastic matrix; $D^{v^{''}}$ is the imaginary part; $η$ is the loss factor; and $i = \sqrt{- 1}$ is the imaginary operator.

At the macroscale, the kinetic equation of a structure system for free vibration is given as Eq. (7):

7

M \ddot{X} + (K_{R} + i K_{I}) X = 0,

where $X$ is the displacement vector of the macrostructure; $M$ is the mass matrix; and $K_{R}$ and $K_{I}$ are the real and imaginary parts of the stiffness matrix, respectively.

The mass matrix and stiffness matrices are expressed as Eq. (8):

8

M = \sum_{i = 1}^{N m} (M_{i}^{b} + M_{i}^{v} + M_{i}^{c}), K_{R} = \sum_{i = 1}^{N m} (K_{i}^{b} + R e (K_{i}^{v}) + K_{i}^{c}), K_{I} = \sum_{i = 1}^{N m} I m (K_{i}^{v}),

where $M_{i}^{b}$ , $M_{i}^{v}$ and $M_{i}^{c}$ are the mass matrices of the $i$ -th element and $K_{i}^{b}$ , $K_{i}^{v}$ and $K_{i}^{c}$ are the stiffness matrices of the $i$ -th element; The superscripts “ $b$ ”, “ $v$ ” and “ $c$ ” stand for base layer, viscoelastic damping layer and constrained layer, respectively; $R e (•)$ and $I m (•)$ represent the real and imaginary parts, respectively; $N m$ is the total number of elements in the macrostructure of the viscoelastic damping sandwich panel.

Based on the modal strain energy method, the $r$ -th order modal loss factor is given by Eq. (9):

9

η_{r} = \frac{Φ_{r}^{T} K_{I} Φ_{r}}{Φ_{r}^{T} K_{R} Φ_{r}},

where $Φ_{r}$ is the $r$ -th order real eigenvector of the viscoelastic damping sandwich plate.

3. Multi-scale topology optimization of viscoelastic damping sandwich panels

3.1. Mathematical model for the multi-scale topology optimization problem

To enhance the ability of viscoelastic damping material to dissipate vibration energy, the multi-scale optimization model of viscoelastic damping sandwich panels is proposed with the minimization of the inverse of the modal loss factor as the optimization objective. The optimization problem is formulated as Eq. (10):

10

\begin{array}{l} F i n d : X (ρ_{i}^{M A}, ρ_{j}^{M I}), \\ M i n i m i z e : f = \sum_{r = 1}^{m} \frac{α_{r}}{η_{r}}, \\ S u b j e c t t o : V_{f}^{M A} \leq \frac{1}{V^{M A}} \sum_{i = 0}^{N m} V_{i}^{M A} ρ_{i}^{M A}, \\ V_{f}^{M I} \leq \frac{1}{V^{M I}} \sum_{j = 0}^{n} V_{j}^{M I} ρ_{j}^{M I}, \\ 0 < ρ_{m i n}^{M A} \leq ρ_{i}^{M A} \leq 1, i = 1, 2, \dots, N m, \\ 0 < ρ_{m i n}^{M I} \leq ρ_{j}^{M I} \leq 1, j = 1, 2, \dots, n, \end{array}

where: $X$ is the design variable, which consists of the macro design variable $ρ_{i}^{M A}$ and the micro design variable $ρ_{j}^{M I}$ ; $α_{r}$ is the weighting factor; $V_{f}^{M A}$ and $V_{f}^{M I}$ are the macrostructural volume fraction and microstructural volume fraction, respectively; $V^{M A}$ is the volume of the macroscopic design domain; $V^{M I}$ is the volume of the unit cell; $V_{i}^{M A}$ is the volume of the $j$ -th element in the macrostructure; $V_{j}^{M I}$ is the volume of the $i$ -th element in the microstructure; $ρ_{m i n}^{M A}$ and $ρ_{m i n}^{M I}$ are the lower limit values of the design variables, both of which take the value of 0.0001; $N m$ is the total number of macro design variables.

At the macroscopic scale, the viscoelastic damping layer and constrained layer are the optimized design regions. To obtain a clear design layout, the Solid Isotropic Microstructure with Penalization (SIMP) interpolation method is adopted, and the mass and stiffness matrices of the $i$ -th element can be written as Eq. (11):

11

M_{i}^{v} = ρ_{i}^{M A} \int_{Ω_{i}} ρ^{H} N^{T} N d Ω_{i}, M_{i}^{c} = ρ_{i}^{M A} \int_{Ω_{i}} ρ^{c} N^{T} N d Ω_{i},

K_{i}^{v} = (ρ_{i}^{M A})^{p} \int_{Ω_{i}} B^{T} D^{H} B d Ω_{i}, K_{i}^{c} = (ρ_{i}^{M A})^{p} \int_{Ω_{i}} B^{T} D^{c} B d Ω_{i},

where $ρ^{c}$ and $D^{c}$ are the density and elasticity matrix of the constrained layer, respectively; $p$ is the penalty factor; $N$ and $B$ are the shape function and strain matrix of the macrostructure, respectively.

Meanwhile, at the microscopic scale, the density and elasticity matrix of the $i$ -th element can be obtained by interpolation, as described by Eq. (12):

12

\begin{array}{l} ρ_{j}^{v} = ρ_{j}^{M I} ρ^{v}, \\ D_{j}^{M I} = (ρ_{j}^{M I})^{p} D^{v}, \end{array}

where $ρ^{v}$ and $D^{v}$ are the density and elasticity matrix of the viscoelastic damping material.

3.2. Sensitivity analysis

On the macroscopic scale, the effect of the eigenvector on the sensitivity of the objective function is considered. The adjoint variable method (AVM) is used to eliminate the sensitivities of the eigenvectors and eigenvalues [19]. Introduce the adjoint variables $μ_{1}$ and $μ_{2}$ into the expression for the inverse of the modal loss factor, as shown in Eq. (13):

13

\frac{1}{η_{r}} = \frac{Φ_{r}^{T} K_{R} Φ_{r}}{Φ_{r}^{T} K_{I} Φ_{r}} + μ_{1} (K_{R} - λ_{r}^{2} M) Φ_{r} + μ_{2} (Φ_{r}^{T} M Φ_{r} - 1),

where $λ_{r}^{2}$ is the $r$ -th order eigenvalue.

The sensitivity of the above equation with respect to the macro design variable $ρ_{i}^{M A}$ can be expressed as Eq. (14):

14

\frac{\partial}{\partial ρ_{i}^{M A}} (\frac{1}{η_{r}}) = (\frac{(Φ_{r}^{T} K_{I} Φ_{r}) (2 Φ_{r}^{T} K_{R}) - (Φ_{r}^{T} K_{R} Φ_{r}) (2 Φ_{r}^{T} K_{I})}{(Φ_{r}^{T} K_{I} Φ)^{2}} + μ_{1} (K_{R} - λ_{r}^{2} M) + 2 μ_{2} Φ_{r}^{T} M) \frac{\partial Φ_{r}}{\partial ρ_{i}^{M A}} - μ_{1} \frac{\partial λ_{r}^{2}}{\partial ρ_{i}^{M A}} M Φ_{r} + μ_{1} (\frac{\partial K_{R}}{\partial ρ_{i}^{M A}} - λ_{r}^{2} \frac{\partial M}{\partial ρ_{i}^{M A}}) Φ_{r} + μ_{2} Φ_{r}^{T} \frac{\partial M}{\partial ρ_{i}^{M A}} Φ_{r} + \frac{(Φ_{r}^{T} K_{I} Φ_{r}) (Φ_{r}^{T} \frac{\partial K_{R}}{\partial ρ_{i}^{M A}} Φ_{r}) - (Φ_{r}^{T} K_{R} Φ_{r}) (Φ_{r}^{T} \frac{\partial K_{I}}{\partial ρ_{i}^{M A}} Φ_{r})}{(Φ_{r}^{T} K_{I} Φ_{r})^{2}} .

To eliminate the terms containing $\frac{\partial Φ_{r}}{\partial ρ_{i}^{M A}}$ and $\frac{\partial λ_{r}^{2}}{\partial ρ_{i}^{M A}}$ , the Eq. (15) needs to be satisfied:

15

\begin{array}{l} \frac{(Φ_{r}^{T} K_{I} Φ_{r}) (2 Φ_{r}^{T} K_{R}) - (Φ_{r}^{T} K_{R} Φ_{r}) (2 Φ_{r}^{T} K_{I})}{(Φ_{r}^{T} K_{I} Φ)^{2}} + μ_{1} (K_{R} - λ_{r}^{2} M) + 2 μ_{2} Φ_{r}^{T} M = 0, \\ μ_{1} M Φ_{r} = 0 . \end{array}

Solving Eq. (15) for the values of the accompanying vectors $μ_{1}$ and $μ_{2}$ gives the sensitivity of the inverse of the modal loss factor, as shown in Eq. (16):

16

\begin{matrix} \frac{\partial}{\partial ρ_{i}^{M A}} (\frac{1}{η_{r}}) = μ_{1} (\frac{\partial K_{R}}{\partial ρ_{i}^{M A}} - λ_{r}^{2} \frac{\partial M}{\partial ρ_{i}^{M A}}) Φ_{r} + μ_{2} Φ_{r}^{T} \frac{\partial M}{\partial ρ_{i}^{M A}} Φ_{r} \end{matrix}

+ \frac{(Φ_{r}^{T} K_{I} Φ_{r}) (Φ_{r}^{T} \frac{\partial K_{R}}{\partial ρ_{i}^{M A}} Φ_{r}) - (Φ_{r}^{T} K_{R} Φ_{r}) (Φ_{r}^{T} \frac{\partial K_{I}}{\partial ρ_{i}^{M A}} Φ_{r})}{(Φ_{r}^{T} K_{I} Φ_{r})^{2}} .

According to Eqs. (8) and (11), the sensitivity of the mass matrix and stiffness matrix with respect to the macro design variable $ρ_{i}^{M A}$ is expressed as Eq. (17):

17

\begin{array}{l} \frac{\partial M}{\partial ρ_{i}^{M A}} = \int_{Ω_{i}} ρ^{H} N^{T} N d Ω_{i} + \int_{Ω_{i}} ρ^{c} N^{T} N d Ω_{i}, \\ \frac{\partial K_{R}}{\partial ρ_{i}^{M A}} = p (ρ_{i}^{M A})^{p - 1} (R e (\int_{Ω_{i}} B^{T} D^{H} B d Ω_{i}) + \int_{Ω_{i}} B^{T} D^{c} B d Ω_{i}), \\ \frac{\partial K_{I}}{\partial ρ_{i}^{M A}} = p (ρ_{i}^{M A})^{p - 1} I m (\int_{Ω_{i}} B^{T} D^{H} B d Ω_{i}) . \end{array}

The sensitivity of the inverse of the modal loss factor with respect to the macro design variable $ρ_{i}^{M A}$ is obtained by substituting Eq. (17) into (16).

At the micro scale, in order to improve the computational efficiency, the influence of the sensitivity of the eigenvectors on the sensitivity of the optimization target is not considered, and the sensitivity of the optimization target with respect to the micro design variable $ρ_{j}^{M I}$ is given by Eq. (18):

18

\frac{\partial}{\partial ρ_{j}^{M I}} (\frac{1}{η_{r}}) = \frac{(Φ_{r}^{T} K_{I} Φ_{r}) (Φ_{r}^{T} \frac{\partial K_{R}}{\partial ρ_{j}^{M I}} Φ_{r}) - (Φ_{r}^{T} K_{R} Φ_{r}) (Φ_{r}^{T} \frac{\partial K_{I}}{\partial ρ_{j}^{M I}} Φ_{r})}{(Φ_{r}^{T} K_{I} Φ_{r})^{2}} .

The sensitivity of the mass matrix and stiffness matrix with respect to the micro design variable $ρ_{j}^{M I}$ is given by Eq. (19):

19

\begin{array}{l} \frac{\partial M}{\partial ρ_{j}^{M I}} = \sum_{i = 1}^{N m} ρ_{i}^{M A} \int_{Ω_{i}} \frac{\partial ρ^{H}}{\partial ρ_{j}^{M I}} N^{T} N d Ω_{i}, \\ \frac{\partial K_{R}}{\partial ρ_{j}^{M I}} = \sum_{i = 1}^{N m} (ρ_{i}^{M A})^{p} \int_{Ω_{i}} B^{T} R e (\frac{\partial D^{H}}{\partial ρ_{j}^{M I}}) B d Ω_{i}, \\ \frac{\partial K_{I}}{\partial ρ_{j}^{M I}} = \sum_{i = 1}^{N m} (ρ_{i}^{M A})^{p} \int_{Ω_{i}} B^{T} I m (\frac{\partial D^{H}}{\partial ρ_{j}^{M I}}) B d Ω_{i} . \end{array}

The sensitivity of the equivalent elasticity matrix $D^{H}$ of the unit cell can be expressed as Eq. (20):

20

\frac{\partial D^{H}}{\partial ρ_{j}^{M I}} = \frac{1}{|Y|} \int_{Y_{j}} (I - b u_{j}) (p (ρ_{j}^{M I})^{p - 1} D^{v}) (I - b u_{j}) d Y_{j} .

3.3. Optimize processes

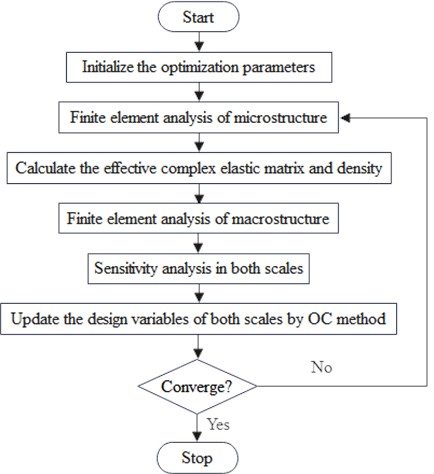
The multi-scale optimization process for viscoelastic damping sandwich panels is shown in Fig. 2, which is as follows:

(1) The viscoelastic damping layer and constrained layer are set to be the design domain and the optimization parameters such as the initial values of macro design variables and micro design variables are initialized.

(2) The finite element model of unit cell is established, and the equivalent material properties of the viscoelastic damping layer are obtained by using the homogenization method.

(3) Based on the equivalent material properties of the unit cell, a macroscopic finite element model of the viscoelastic damping sandwich plate is established, and its modal analysis is performed to obtain the modal loss factor.

(4) The sensitivity of the optimization objective in both scales are computed via Eqs. (16, 18).

(5) The optimization model is solved and the values of macro design variables and micro design variables are updated using OC method.

(6) If the optimization objective value is less than 0.001 for 20 consecutive iterations, the convergence condition is reached and the loop ends, otherwise, repeat steps (2)-(6) until the convergence condition is reached.

Fig. 2Multi-scale topology optimization process

4. Numerical examples

The viscoelastic damping sandwich panel with two short sides clamped is shown in Fig. 3. Its length and width are 0.4 m and 0.2 m, respectively. The thicknesses of the base plate, viscoelastic damping layer and constrained layer are 0.001 m, 0.0002 m and 0.0001 m, respectively. The base plate and the constrained layer are aluminum alloys with density 2700 kg/m³, elasticity modulus 70 GPa and Poisson’s ratio 0.3, respectively. The real part of the complex elastic modulus, loss factor and Poisson’s ratio of the viscoelastic damping material are 20 MPa, 0.5 and 0.495, respectively. At the microscopic scale, the finite element model of unit cell is established using eight-node hexahedron element, on which periodic symmetry constraints and external loads caused by a predetermined unit strain are applied [20]. Using homogenization theory, the microstructure is required to be much smaller than the macrostructure and the length, width and height of the unit cell are dimensionless 1×1×1. The microstructure is divided to 25×25×25. At the macroscopic scale, the viscoelastic damping sandwich panel is divided to 32×16. A type of three-layer four-node rectangular element with seven degrees of freedom on every node [21] is used to build the finite element model. The finite element models and optimization program are all implemented in MATLAB.

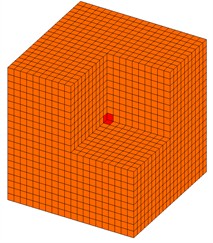
The initial configuration of the unit cell is shown in Fig. 4, with the red region representing the initial value of the design variable as 1 and the orange region representing the initial value of the design variable as the value of the microstructure volume constraint. The initial values of the macro design variables are equal to macro volume constraints.

Fig. 3A restrained damping plate with two fixed short edges

Fig. 4Initial configuration of a viscoelastic damping cell (with the upper right front hidden)

To verify the correctness of the proposed method, three different design objectives are considered, which are (1) minimization of the inverse of the first-order modal loss factor, (2) minimization of the inverse of the second-order modal loss factor, (3) minimization of the inverse of the sum of the first two orders of modal loss factors. The macrostructural volume fraction and microstructural volume fraction are both 0.6. The optimization results are shown in Fig. 5-7. It can be seen that both macro and micro optimization configurations are different as the optimization objective changes. From the macroscopic optimized configurations in Figs. 5(a) and 6(a), it can be seen that the constrained damping material is mainly distributed in the region of the high modal strain energy to maximize the dissipation of vibration energy. From Fig. 7, it can be seen that the optimization result of maximizing the sum of the first two orders of modal loss factors is a combination of the optimization results of example 1 and example 2.

Fig. 5The optimization results of example 1

a) Macrostructure

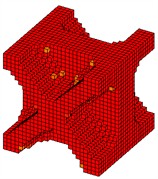
b) Microstructure

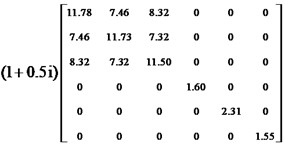
c) $D^{H}$ (MPa)

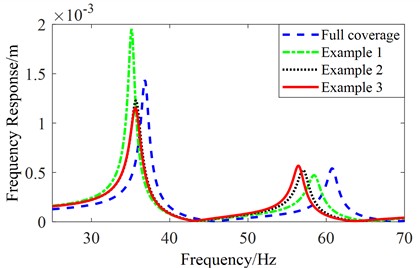
The modal loss factors of the full coverage structure and the optimized results are compared, as shown in Table 1. Fig. 8 shows the frequency responses of the full coverage structure and the optimized structures. From Table 1 and Fig. 8, it can be found that when the optimization objective is a single modal order, the modal loss factor of the objective modal order is the largest and the resonant peak is the smallest. Example 3 obtains a better equilibrium in the first two modes. The above analysis shows that the damping characteristics of the viscoelastic damping sandwich panel are effectively improved by the multi-scale optimization design of the viscoelastic damping sandwich panel.

Fig. 6The optimization results of example 2

a) Macrostructure

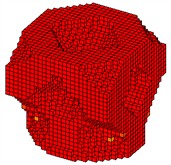
b) Microstructure

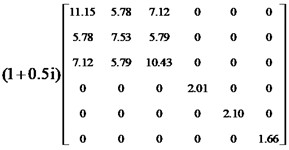
c) $D^{H}$ (MPa)

Fig. 7The optimization results of example 3

a) Macrostructure

b) Microstructure

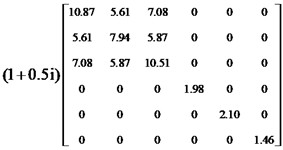
c) $D^{H}$ (MPa)

Table 1Comparison of modal loss factors

	The first order	The second order	The sum of the first two orders
Full coverage	0.029 8	0.025 6	0.055 4
Example 1	0.040 3	0.027 4	0.067 7
Example 2	0.025 7	0.031 9	0.057 6
Example 3	0.038 7	0.029 5	0.068 2

Fig. 8Frequency response diagram

The effects of volume constraints on the optimized configuration are analyzed. The optimization objective is to minimize the inverse of the first-order modal loss factor. Two combinations of $V_{f}^{M A}$ and $V_{f}^{M I}$ are tested. The optimization results are shown in Fig. 9 and Fig. 10. Comparing Figs. 5(a) and 9(a), the change in microscopic volume fraction resulted in a significant change in the macroscopic optimized configuration. From Figs. 9(b) and 10(b), it can be seen that the change in macroscopic volume fraction has little effect on the micro-configuration, and the equivalent transverse shear modulus of the micro optimized configuration is unchanged, as in Figs. 9(c) and 10(c).

Fig. 9The optimization results of example 4 (VfMA= 0.6, VfMI=0.4)

a) Macrostructure

b) Microstructure

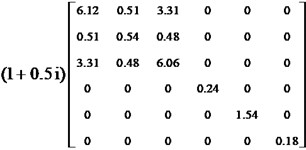
c) $D^{H}$ (MPa)

Fig. 10The optimization results of example 5 (VfMA= 0.7, VfMI=0.4)

a) Macrostructure

b) Microstructure

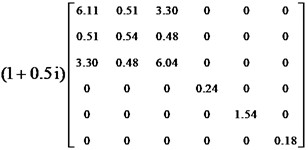
c) $D^{H}$ (MPa)

5. Conclusions

1) A multi-scale optimal design method for viscoelastic damping sandwich panels is proposed, which realizes its collaborative optimal design on both macro and micro scales, and obtains the macroscopic optimal layout of the constrained damping material and microscopic configuration of the viscoelastic damping material.

2) The effects of different optimization targets on the optimized configuration are analyzed. The optimization results show that when maximizing the modal loss factor of a single order is taken as the optimization target, the modal loss factor of the target order is the largest, and the resonant peak of this order is the smallest. When maximizing the sum of the modal loss factor of the first two orders is taken as the target, the performance of the optimal structure obtains a better balance in the first two modes.

3) The effects of macroscopic and microscopic volume fractions on the optimized configurations are analyzed, and the optimization results showed that the change in the microscopic volume fraction resulted in a significant change of the macroscopic optimized configuration, while the change in the macroscopic volume fraction has very little effect on the microscopic configuration.

4) Future work will exhibit much interest in exploring the performance variations of viscoelastic damping materials across a spectrum of frequency and temperature conditions. Additionally, the development of a multi-scale model that accounts for the interactions between various types of unit cells within the entire design region will be a significant focus.

References

Z. Huang, Z. Qin, and F. Chu, “Vibration and damping characteristics of sandwich plates with viscoelastic core,” Journal of Vibration and Control, Vol. 22, No. 7, pp. 1876–1888, Aug. 2014, https://doi.org/10.1177/1077546314545527

Publisher
S. Y. Kim, C. K. Mechefske, and I. Y. Kim, “Optimal damping layout in a shell structure using topology optimization,” Journal of Sound and Vibration, Vol. 332, No. 12, pp. 2873–2883, Jun. 2013, https://doi.org/10.1016/j.jsv.2013.01.029

Publisher
T. Yamamoto, T. Yamada, K. Izui, and S. Nishiwaki, “Topology optimization of free-layer damping material on a thin panel for maximizing modal loss factors expressed by only real eigenvalues,” Journal of Sound and Vibration, Vol. 358, pp. 84–96, Dec. 2015, https://doi.org/10.1016/j.jsv.2015.08.019

Publisher
J. Zhang, Y. Chen, J. Zhai, Z. Hou, and Q. Han, “Topological optimization design on constrained layer damping treatment for vibration suppression of aircraft panel via improved Evolutionary Structural Optimization,” Aerospace Science and Technology, Vol. 112, p. 106619, May 2021, https://doi.org/10.1016/j.ast.2021.106619

Publisher
G. Delgado and M. Hamdaoui, “Topology optimization of frequency dependent viscoelastic structures via a level-set method,” Applied Mathematics and Computation, Vol. 347, pp. 522–541, Apr. 2019, https://doi.org/10.1016/j.amc.2018.11.014

Publisher
Z. Fang and L. Zheng, “Topology optimization for minimizing frequency response of constrained layer damping plates,” Journal of Vibroengineering, Vol. 17, No. 6, pp. 2763–2780, 2015.

Publisher
A. Takezawa, M. Daifuku, Y. Nakano, K. Nakagawa, T. Yamamoto, and M. Kitamura, “Topology optimization of damping material for reducing resonance response based on complex dynamic compliance,” Journal of Sound and Vibration, Vol. 365, pp. 230–243, Mar. 2016, https://doi.org/10.1016/j.jsv.2015.11.045

Publisher
Z. Hu, S. Sun, O. Vambol, and K. Tan, “Topology optimization of laminated composite structures under harmonic force excitations,” Journal of Composite Materials, Vol. 56, No. 3, pp. 409–420, Nov. 2021, https://doi.org/10.1177/00219983211052605

Publisher
W. Zheng, T. Yang, Q. Huang, and Z. He, “Topology optimization of PCLD on plates for minimizing sound radiation at low frequency resonance,” Structural and Multidisciplinary Optimization, Vol. 53, No. 6, pp. 1231–1242, Dec. 2015, https://doi.org/10.1007/s00158-015-1371-4

Publisher
L. Ma and L. Cheng, “Topological optimization of damping layout for minimized sound radiation of an acoustic black hole plate,” Journal of Sound and Vibration, Vol. 458, pp. 349–364, Oct. 2019, https://doi.org/10.1016/j.jsv.2019.06.036

Publisher
J. F. A. Madeira, A. L. Araújo, and C. M. Mota Soares, “Multiobjective optimization of constrained layer damping treatments in composite plate structures,” Mechanics of Advanced Materials and Structures, Vol. 24, No. 5, pp. 427–436, Apr. 2017, https://doi.org/10.1080/15376494.2016.1190427

Publisher
J. F. A. Madeira, A. L. Araújo, C. M. Mota Soares, and C. A. Mota Soares, “Multiobjective optimization for vibration reduction in composite plate structures using constrained layer damping,” Computers and Structures, Vol. 232, p. 105810, May 2020, https://doi.org/10.1016/j.compstruc.2017.07.012

Publisher
W. Chen and S. Liu, “Topology optimization of microstructures of viscoelastic damping materials for a prescribed shear modulus,” Structural and Multidisciplinary Optimization, Vol. 50, No. 2, pp. 287–296, Feb. 2014, https://doi.org/10.1007/s00158-014-1049-3

Publisher
H. Zhang, X. Ding, Q. Wang, W. Ni, and H. Li, “Topology optimization of composite material with high broadband damping,” Computers and Structures, Vol. 239, p. 106331, Oct. 2020, https://doi.org/10.1016/j.compstruc.2020.106331

Publisher
W. Chen and S. Liu, “Microstructural topology optimization of viscoelastic materials for maximum modal loss factor of macrostructures,” Structural and Multidisciplinary Optimization, Vol. 53, No. 1, pp. 1–14, Aug. 2015, https://doi.org/10.1007/s00158-015-1305-1

Publisher
Q. Liu, D. Ruan, and X. Huang, “Topology optimization of viscoelastic materials on damping and frequency of macrostructures,” Computer Methods in Applied Mechanics and Engineering, Vol. 337, pp. 305–323, Aug. 2018, https://doi.org/10.1016/j.cma.2018.03.044

Publisher
Z. Fang, L. Yao, S. Tian, and J. Hou, “Microstructural topology optimization of constrained layer damping on plates for maximum modal loss factor of macrostructures,” Shock and Vibration, Vol. 2020, pp. 1–13, Oct. 2020, https://doi.org/10.1155/2020/8837610

Publisher
H. Zhang, X. Ding, H. Li, and M. Xiong, “Multi-scale structural topology optimization of free-layer damping structures with damping composite materials,” Composite Structures, Vol. 212, pp. 609–624, Mar. 2019, https://doi.org/10.1016/j.compstruct.2019.01.059

Publisher
D. Zhang, Y. Wu, X. Lu, and L. Zheng, “Topology optimization of constrained layer damping plates with frequency – and temperature-dependent viscoelastic core via parametric level set method,” Mechanics of Advanced Materials and Structures, Vol. 29, No. 1, pp. 154–170, Jan. 2022, https://doi.org/10.1080/15376494.2021.1938302

Publisher
G. Dong, Y. Tang, and Y. F. Zhao, “A 149 line homogenization code for three-dimensional cellular materials written in Matlab,” Journal of Engineering Materials and Technology, Vol. 141, No. 1, p. 01100, Jan. 2019, https://doi.org/10.1115/1.4040555

Publisher
Z. Huang, Z. Qin, and F. Chu, “Damping mechanism of elastic-viscoelastic-elastic sandwich structures,” Composite Structures, Vol. 153, pp. 96–107, Oct. 2016, https://doi.org/10.1016/j.compstruct.2016.05.105

Publisher

About this article

Received

15 July 2024

Accepted

10 January 2025

Published

22 January 2025

SUBJECTS

Vibration control, generation and harvesting

DOI

https://doi.org/10.21595/jve.2025.24360

Keywords

viscoelastic damping material

multi-scale design

topology optimization

modal loss facto

Acknowledgements

This research is supported by Science and Technique Research Project of Henan Province (Grant No. 222102240116), the Plan of Key Research Projects of Higher Education of Henan Province (Grant No. 24A460024) and the Science and technology open cooperation project of Henan Academy of Sciences (Grant No. 220907016). These financial supports are gratefully acknowledged.

Data Availability

The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

Author Contributions

Zhanpeng Fang carried out the modeling and wrote the paper, Haoping An analyzed the calculation results, Yanqiu Xiao carried out the simulation of the work. All authors have read and agreed to the published version of the manuscript.

Conflict of interest

The authors declare that they have no conflict of interest.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Research article

2023 02 14

Identification of the parameters of a composite material by experimental-computational damping research

V. P. Eremin, E. E. Guseva, A. A. Bolshikh

Research article

2022 03 17

Optimization of damping pad distribution on body-in-white car structure

Dávid Sipos, Marcell Ferenc Treszkai, Dániel Feszty

Research article

2020 09 30

A fractional Maxwell approach for the shock response of viscoelastic oscillator

Yuan Qin, Dagang Sun, Zhanlong Li, Yao Wang, Chao Chang, Bao Sun

Research article

2019 04 25

Use of viscous fluid dampers for the improvement of the seismic response of RC structures

Angie Catalina Lamprea Pineda, Luis Fernando Garzón Amortegui, Claudio Chesi

Z. Fang, H. An, and Y. Xiao, “Multi-scale optimization design of viscoelastic damping sandwich plate,” Journal of Vibroengineering, Vol. 27, No. 2, –11, Jan. 2025, https://doi.org/10.21595/jve.2025.24360

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jve.2025.24360
UR  - https://doi.org/10.21595/jve.2025.24360
TI  - Multi-scale optimization design of viscoelastic damping sandwich plate
T2  - Journal of Vibroengineering
AU  - Fang, Zhanpeng
AU  - An, Haoping
AU  - Xiao, Yanqiu
PY  - 2025
DA  - 2025/01/22
PB  - Extrica
VL  - 27
IS  - 2
SN  - 1392-8716
SN  - 2538-8460
ER  - 

Copy Ris

Copied to clipboard!

 @article{Fang_2025, title={Multi-scale optimization design of viscoelastic damping sandwich plate}, ISSN={2538-8460}, url={https://doi.org/10.21595/jve.2025.24360}, DOI={10.21595/jve.2025.24360}, journal={Journal of Vibroengineering}, publisher={JVE International Ltd.}, author={Fang, Zhanpeng and An, Haoping and Xiao, Yanqiu}, year={2025}, month=jan }

Copy Bibtex

Copied to clipboard!

[1]Z. Fang, H. An, and Y. Xiao, “Multi-scale optimization design of viscoelastic damping sandwich plate,” Journal of Vibroengineering, Jan. 2025, doi: 10.21595/jve.2025.24360.

Copy IEEE

Copied to clipboard!

Fang, Zhanpeng, Haoping An, and Yanqiu Xiao. “Multi-Scale Optimization Design of Viscoelastic Damping Sandwich Plate.” Journal of Vibroengineering, January 22, 2025. https://doi.org/10.21595/jve.2025.24360.

Copy Chicago

Copied to clipboard!

Multi-scale optimization design of viscoelastic damping sandwich plate

Abstract

1. Introduction

2. Multi-scale viscoelastic damping sandwich plate and its damping property

2.1. Homogenization analysis of viscoelastic damping layer

2.2. Damping property of viscoelastic damping sandwich plate

3. Multi-scale topology optimization of viscoelastic damping sandwich panels

3.1. Mathematical model for the multi-scale topology optimization problem

3.2. Sensitivity analysis

3.3. Optimize processes

4. Numerical examples

5. Conclusions

References

About this article

Related Articles