Study on dynamic response analysis and vibration control of TV tower under wind-rain load excitation

2.1. Finite element model of the television tower

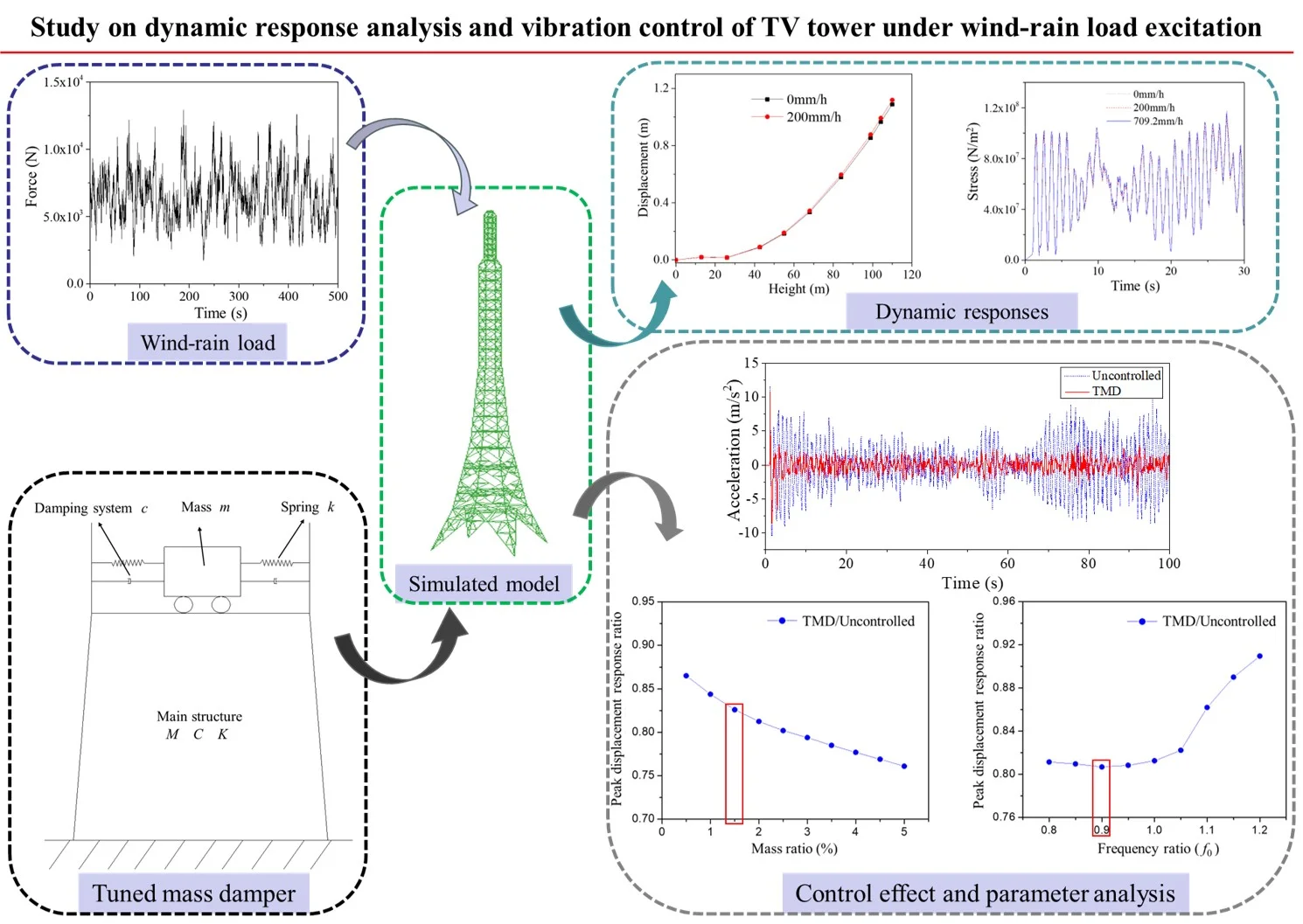
The television tower has a total height of 110 meters, with the primary structural members primarily made of Q420 steel. The diagonal and auxiliary members are mainly composed of Q345 and Q235 steel. The main components are steel pipes, with some auxiliary members made of angle steel. Based on actual engineering data, the structure was modeled using the finite element software ABAQUS. BEAM elements (B31) were selected to simulate the television tower, fully considering the bending moments of the structural components. The tower base is connected in a fixed manner. The dimensions of the structure and the model are shown in Fig. 1.

Fig. 1Dimensional drawing and model diagram of the television tower

2.2. Analysis of dynamic characteristics

To validate the finite element model developed, modal analysis was performed using ABAQUS to determine the model’s modal characteristics. The first ten natural frequencies of the television tower structure are presented in Table 1. The first and second mode shapes of the television tower are illustrated in Fig. 2. These modal analysis results will be utilized in the analysis of structural dynamic response under wind and rain loads, as well as in the study of vibration control.

Fig. 2The first two mode shapes of the television tower

a) First mode shape

b) Second mode shape

2.3. Generation of wind-rain load

In this study, the dynamic time history of wind loads acting on the television tower was simulated using the linear filtering method. The actual wind speed was modeled by superimposing fluctuating wind speed onto the mean wind speed. The Davenport spectrum was selected to represent the fluctuating wind speed spectrum [11], with its expression as follows:

where, $X=1200n/{\bar{v}}_{10}$; $n$ is the frequency (Hz); ${\bar{v}}_{10}$ is the mean wind speed at a standard height of 10 meters (m/s); and $K$ is the ground roughness coefficient.

Based on the conversion relationship between wind speed and wind pressure, the wind load time history can be obtained from the wind speed time history [12]:

where ${\mu }_S$ is the shape coefficient of the structure; $V\left(t\right)$ is the wind speed value; and $A$ is the windward area.

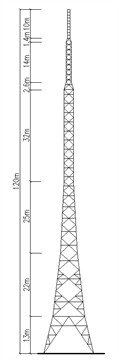
Table 2Parameters of the simulation points on the TV tower

	Simulation point	Simulation interval (m)	Height of simulation point (m)	Bearing area (m2)
	7	92-110	101	20.044
	6	76-92	84	30.476
	5	60-76	68	15.424
	4	49.17-60	55	11.011
	3	35-49.17	42	13.823
	2	13-35	24	12.146
	1	0-13	7	10.696
Note: Bearing area refers to the projected area of the windward surface components

Following the equivalent simplified method with multiple regions and nodes used by relevant scholars [13-16] for analyzing wind-induced responses in tall steel structures, the television tower was divided into reasonable and effective sections. Each region selected an appropriate height for simulation points. The positions of the intervals, the heights of the simulation points, and the areas subjected to wind pressure are shown in Table 2. The television tower, with a total height of 110 meters, was divided into seven sections from top to bottom, each with a simulated length of approximately 15 meters. The tower's lateral width decreases from bottom to top: from the base of the first section to the top of the fourth section, the lateral width gradually reduces from 9 meters to 1.75 meters. From the fifth section to the sixth section, the width remains constant at 1.75 meters. At the 94.6-meter mark of the seventh section, the width abruptly changes to 0.9 meters and remains unchanged to the top of the tower.

When the basic wind speed is 20 m/s, the wind speed time histories for simulation points 3 and 7 are shown in Fig. 3. Fig. 4 compares the target power spectrum with the simulated power spectrum and includes the autocorrelation curve. As seen in the figure, the simulated spectrum closely matches the target spectrum, indicating a consistent trend. The autocorrelation of the simulated points at different times is weak, demonstrating that the order and parameters selected for the linear filtering method are reliable and effective for simulating wind loads.

The wind load time history curves for different simulation points were calculated using the wind load formula. The wind load time history curves for simulation points 3 and 7 are shown in Fig. 5. These wind load time histories will be applied to the television tower for subsequent structural response analysis.

Fig. 3Time history of simulated point wind speed

a) Simulation point 3

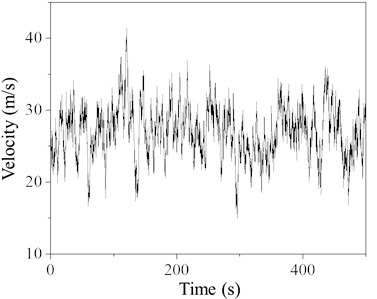
b) Simulation point 7

Fig. 4Comparison between simulated spectrum and target spectrum

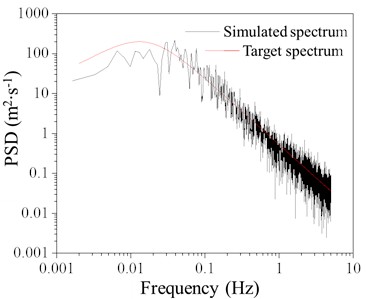
a) Simulation point 3

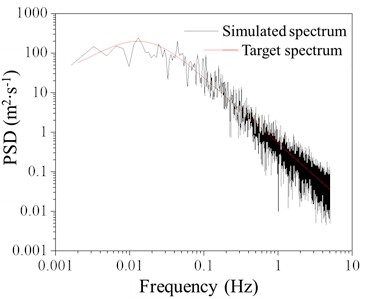
b) Simulation point 7

The forces exerted by raindrops on structures under horizontal wind and gravity are complex. Currently, there is no consensus on a unified rain load calculation model. This paper synthesizes existing research on rain load calculation models and adopts the model derived by Li et al. [3]. Based on the momentum theorem, assuming a raindrop falls as a sphere with an impact duration of $\tau =d/2v$, the impact force of a single raindrop can be simplified as:

Fig. 5Time history of simulated point wind load

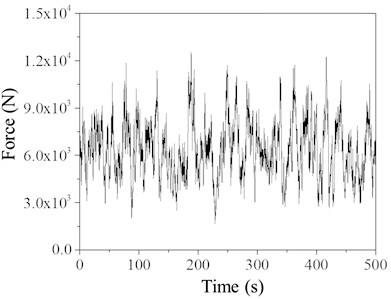
a) Simulation point 3

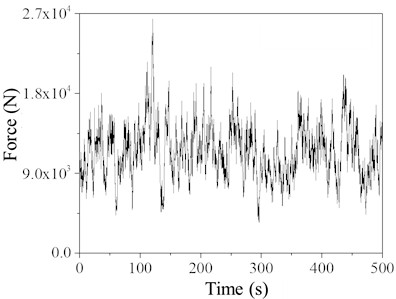
b) Simulation point 7

When applied to a finite element structure, this can be converted into a uniformly distributed load as follows:

where $A$ is the area of impact, given by $A=\pi d^2/4$; $B$ is the width of the structural or component cross-section; and $\alpha$ represents the raindrop occupancy rate in the air, defined as $\alpha =\pi d^{3}n/6$, where $n$ is the number density of raindrops with diameter $d$ per unit volume of air, as listed in Table 3. For lattice structures like TV towers, the rain-affected area is doubled, meaning the component cross-section width is also doubled. Substituting and rearranging yields:

Rainfall intensity is described by the amount of precipitation per unit time. Table 4 presents seven rainfall categories based on the depth of water accumulated on the ground over 24 hours, along with recorded extreme precipitation values in the region. For simplicity in subsequent calculations and considering the research objectives and operational requirements, this study selects two representative rainfall intensities for each scenario: 200 mm/h for heavy rain and 709.2 mm/h for extreme rain. Rain load time history curves for each simulation point are determined based on these rainfall intensities. When the rainfall intensity is 200 mm/h, the rain load time history curves for simulation points 3 and 7 are shown in Fig. 6.

Fig. 7 shows the wind and rain load time history curves for simulation points 3 and 7 on the TV tower. These curves are obtained by summing the wind loads and rain loads calculated from Eq. (2) and Eq. (5). Using the established finite element model of the TV tower and the explicit analysis method in ABAQUS finite element software, the wind and rain load time histories are applied to the nodes of seven segments of the TV tower. Nonlinear time history analysis is then performed to study the dynamic response of the TV tower under various wind speeds and rainfall intensities. Each scenario involves two load steps: one for self-weight and one for combined wind and rain loads, with duration of 1 second and 300 seconds, respectively.

Fig. 6Time history of simulated point rain load (Rain intensity 200 mm/h)

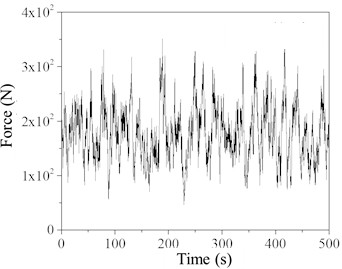
a) Simulation point 3

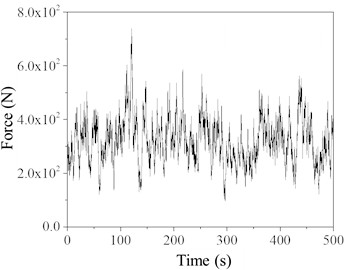
b) Simulation point 7

Fig. 7Time history of simulated point wind-rain load (Rain intensity 200 mm/h)

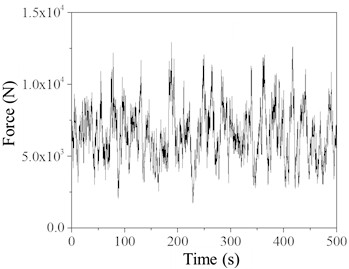
a) Simulation point 3

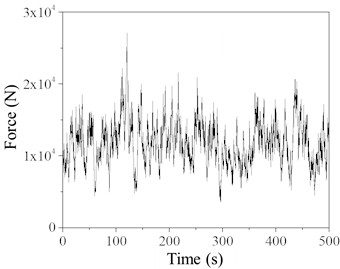
b) Simulation point 7

3.1. Effect of different rain intensities

When the basic wind speed is 30 m/s and the rainfall intensities are 0 and 200 mm/h, the variation curves of node displacement and main member axial force along the height of the TV tower under the separate and combined actions of wind and rain loads are shown in Fig. 8-9. As observed from the figures, the node displacement increases with height, and the rate of increase accelerates. The wind-rain load results in greater node displacements, especially near the top of the tower, compared to the wind load alone. For the main member axial force, it changes slowly with height below 60 meters. However, above 60 meters, the axial force decreases rapidly with height, with a sudden change occurring at 94.6 meters. This abrupt change is attributed to the geometric characteristics of the TV tower, where there is a sudden change in the lateral dimension at this height.

The dynamic response of the TV tower was calculated for a basic wind speed of 30 m/s under rainfall intensities of 0 mm/h, 200 mm/h, and 709.2 mm/h. The node displacement and acceleration time history curves at the top of the TV tower were extracted, as well as the stress time history curves for element 1572 at the top of the tower and element 45 at the minimum cross-section height of 60 meters. The specific calculation results are as follows.

Fig. 8Variation of node displacement along height

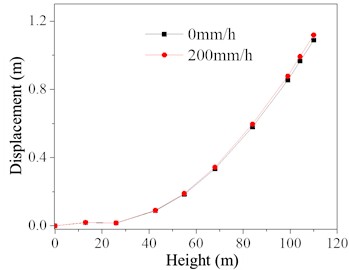
Fig. 9Variation of main material axial force along height

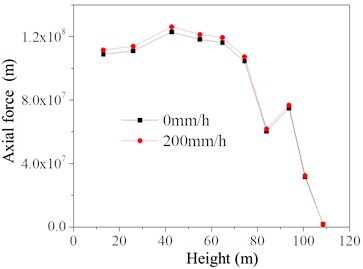
Fig. 10Top dynamic response of TV tower

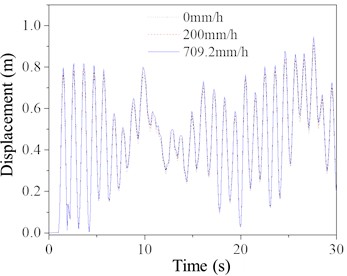
a) Time history of displacement

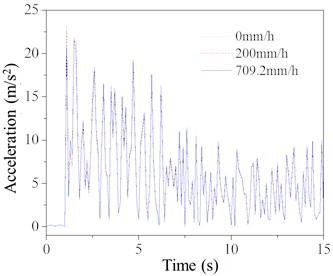
b) Time history of acceleration

Fig. 10 presents the time history curves of node displacement and acceleration at the top of the TV tower. Although the load duration is 300 seconds, only a portion of the time is displayed for clarity. As seen in the figure, the dynamic response of the TV tower is greater under a rainfall intensity of 709.2 mm/h compared to 0 mm/h and 200 mm/h, but the overall increase is not particularly significant. The dynamic responses under 0 mm/h and 200 mm/h rainfall intensities show minimal differences.

Fig. 11Compressive stress of the elements on the compression side of TV tower

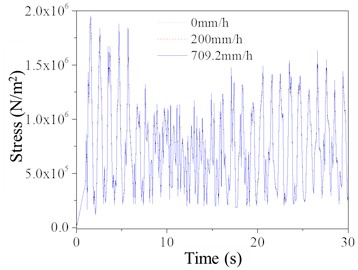
a) Element 1572

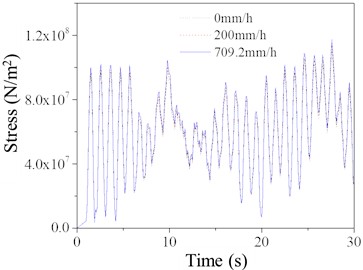
b) Element 45

The time history curves of compressive stress for elements on the compressed side of the TV tower is shown in Fig. 11. Element 1572 represents a main structural member at the top of the tower, and its stress level is not comparable to the stress level of element 45, which is a main structural member at a height of 60 meters. This indicates that structural failure is more likely to occur at the 60-meter height than at the top of the tower. For the compressive stress of element 45, the stress is higher under a rainfall intensity of 709.2 mm/h compared to 0 mm/h and 200 mm/h, and the increase is more significant than for element 1572. Therefore, in subsequent analyses, to simplify the results, only the stress response of element 1572 will be extracted and analyzed for the TV tower.

3.2. Effect of different wind speeds and rain intensities

The wind-rain load time histories simulated in the previous section were applied to the TV tower under basic wind speeds of 20, 30, and 40 m/s, and rainfall intensities of 0 mm/h, 200 mm/h, and 709.2 mm/h. The dynamic response characteristics of the TV tower were analyzed for each combination of wind speed and rainfall intensity. The maximum values of displacement response at the top node, acceleration response at the top node, and compressive stress in element 45 were extracted. The specific results are as follows.

Table 5 shows the maximum displacement values at the top node of the TV tower for various basic wind speeds and rainfall intensities. The data indicates that, for different basic wind speeds, changing the rainfall intensity has a minimal effect on the increase in the maximum displacement of the top node. Specifically, under a rainfall intensity of 200 mm/h, the increase is approximately 2.8 %, and under 709.2 mm/h, it is approximately 6.0 %. This suggests that basic wind speed has little impact on the displacement changes at the top node under different rainfall intensities. According to the “Code for Design of Tall Structures”, the horizontal displacement of the top node of a self-supporting tower should not exceed 1/50 of the tower’s height under wind load-dominant load combinations. Under the condition of a basic wind speed of 40 m/s and a rainfall intensity of 709.2 mm/h, the top node displacement reaches 2.110 meters, which is below the limit of 2.2 meters. This indicates that while the displacement is within the permissible range, it is very close to the limit.

The maximum acceleration values at the top node of the TV tower for various basic wind speeds and rainfall intensities are presented by Table 6. The data reveals that the variation in acceleration at the top node follows a pattern similar to that of displacement. Basic wind speed has little impact on the acceleration changes at the top node under different rainfall intensities. The maximum increase in structural response due to extreme rain load is 6 %, indicating that rain load can be neglected under lighter rainfall conditions. However, in regions with intense precipitation, the impact of rainfall on structural response should be considered.

Table 7 presents the maximum compressive stress values for element 45 on the compressed side of the TV tower under different basic wind speeds and rainfall intensities. The data indicates that the increase in maximum compressive stress due to rainfall intensity grows with increasing basic wind speed. For a rainfall intensity of 200 mm/h, the stress increase ranges from 2.59 % to 2.76 % as the basic wind speed increases from 20 m/s to 40 m/s. For a rainfall intensity of 709.2 mm/h, the stress increase ranges from 5.60 % to 5.92 % over the same wind speed range. Under the condition of a 40 m/s basic wind speed and 0 mm/h rainfall intensity, the maximum compressive stress for element 45 reaches 2.50×10⁸ N/mm², which exceeds the yield strength of the main structural member (2.35×10⁸ N/mm²). This indicates that at a basic wind speed of 40 m/s, the TV tower has already entered a state of plastic buckling and failure.

Fig. 12Dynamic response of TV tower under different basic wind speeds and rainfall intensities

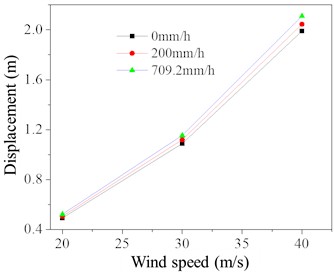
a) Maximum displacement of the top node

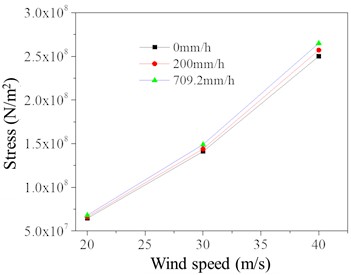
b) Extreme compressive stress of element 45 on the compression side

The maximum displacement of the top node of the TV tower and the maximum compressive stress of the 45 compression elements under different basic wind speeds and rain intensities are shown in Fig. 12. As illustrated, with increasing basic wind speed and rain intensity, the dynamic response of the TV tower also increases, exhibiting a nonlinear trend. However, from the curves in the figure, it can be inferred that when the basic wind speed is around 38 m/s, the maximum compressive stress in the 45 compression elements of the TV tower reaches the yield strength of 2.35×10⁸ N/mm², leading to buckling of the main structural members of the tower.

3.3. Analysis of the dynamic response of structures induced by wind and rain

To further elucidate the entire dynamic response process of the TV tower under the combined action of wind and rain loads, a more detailed analysis is conducted. Taking a basic wind speed of 50 m/s and a rain intensity of 200 mm/h, the stress conditions of the tower’s structural members at different time points are examined, as shown in Fig. 13. At $t=$1.5 s, the main structural member on the leeward side at a height of 60 m (the fifth section) of the TV tower first yields. The internal forces within the tower’s main structure are redistributed. As the wind and rain loads continue, at $t=$11.6 s, the main structural member on the leeward side of the fourth section begins to yield. The number of yielding members in the TV tower increases, altering the load transfer paths. The stress on the members surrounding the yielding ones increases, leading to structural failure as the plastic stage is reached. From the above analysis, it is concluded that the compressive members on the leeward side at a height of 60 m (the fifth section) of the TV tower are the most prone to yield and enter the plastic stage.

Fig. 13Stress distribution of TV tower components

a)$t=$1.5 s

b)$t=$11.6 s

c)$t=$23.6 s

4.1. TMD vibration reduction mechanism and parameter design

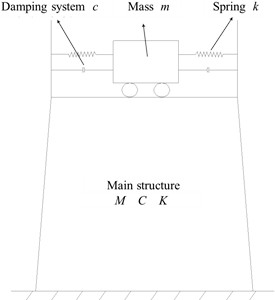
A Tuned Mass Damper (TMD) consists of three main components: a spring, a damper, and a mass block. The principle behind TMD is to tune the frequency of the vibration control system to match the frequency of the main structure. Through the interaction between the TMD and the main structure, energy is transferred, thereby reducing the vibration response of the main structure. The dynamic characteristics of the main structure change when a TMD is installed. When the main structure is subjected to external excitations, the inertia of the TMD’s mass block exerts a counteracting force on the original structure. During this process, the damping system effectively dissipates energy, significantly reducing the structural vibration response.

The simplified model of the TMD is shown in Fig. 14, where $m$ represents the mass of the TMD system, $k$ is the spring stiffness, and $c$ is the damping coefficient. The TMD system can be considered a substructure, primarily controlling the first mode of vibration of the main structure by tuning to the main structure’s first natural frequency. Since the maximum displacement in the first mode occurs at the top of the structure, the vibration control device is optimally placed at or near the top of the main structure. This placement maximizes the vibration reduction benefits of the TMD. The TMD system is connected to the main structure using springs and dampers at both ends, which link the mass block to the main structure.

In this study, the finite element software ABAQUS is used to numerically simulate the TMD. The springs and dampers are modeled using the Spring/Dashpots module, and the mass block is modeled as a Point Mass.

Based on the analysis of the dynamic characteristics of the structure, the first mode frequency in the $X$-direction of the TV transmission tower is 0.956 Hz. The total mass of the main structure is $M=$77311 kg. Unless otherwise specified, the mass ratio ${\mu }_m$ is taken as 2 %, representing the ratio of the TMD mass to the total mass of the main structure, resulting in a TMD mass of $m=$1546 kg.

Fig. 14Simplified model of tuned mass damper

The optimal frequency ratio for the TMD can be determined according to Den [6]:

where, ${\mu }_m$ represents the mass ratio, which is set at 2 %.

The optimal total stiffness of the TMD system can be calculated using the following formula:

where, $m$ represents the mass of the TMD system. In this study, the stiffness of the TMD system is provided by two springs at the ends, which are connected in series. Therefore, the effective stiffness is halved, resulting in$\mathrm{}{k}_1=k_2=k/2$. The natural frequency $\omega$ of the structure can be calculated using the following formula:

where $f$ is the frequency of the structure. In this study, the TMD system is tuned to the first mode frequency of the main structure, which is 0.956 Hz.

The optimal damping for the TMD system can be calculated using the following formula:

where ${\xi }_o$ is the damping ratio of the TMD system, which can be calculated using the following formula:

Based on the above design process, the TMD parameters suitable for the TV tower structure described in this study are listed in Table 8.

4.2. Control effect analysis

To verify the effectiveness of the TMD and evaluate the control performance of the vibration mitigation device, the peak reduction ratio and the root mean square (RMS) reduction ratio are selected as the criteria. The vibration reduction ratio is defined as follows:

where, $R_0$ represents the response of the structure without control, and $R_{TMD}$ represents the response of the structure under TMD control.

The results of the finite element dynamic response analysis indicate that the acceleration time history curve at the top of the signal transmission tower under extreme rainfall and wind loads is compared in Fig. 15. The acceleration time history curves for the controlled and uncontrolled cases show that both cases exhibit significant peaks around 1.1 seconds. However, after 1.1 seconds, the TMD’s vibration control capability is clearly demonstrated. The acceleration time history curve under TMD control consistently shows lower responses at every time point compared to the uncontrolled structure. The vibration reduction effect of the TMD varies with different basic wind speeds. Based on the envelope of the acceleration curve for the uncontrolled structure, the acceleration response at the top of the signal transmission tower under TMD control remains entirely within the range of the uncontrolled response. This indicates that the TMD provides stable vibration control and has a notable advantage in managing wind and rain loads.

Fig. 15Time history curve of top acceleration of TV tower under wind-rain load

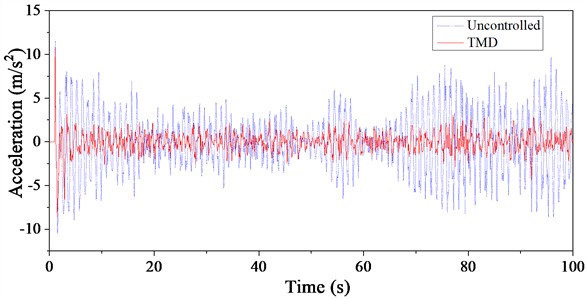
a) Basic wind speed: 20 m/s

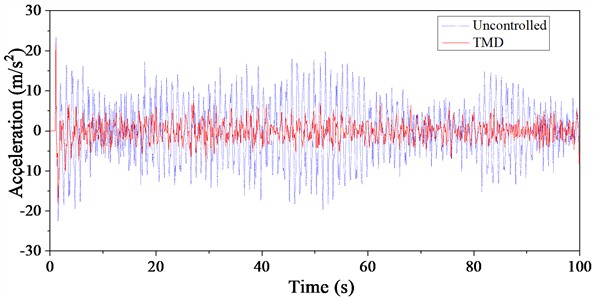
b) Basic wind speed: 30 m/s

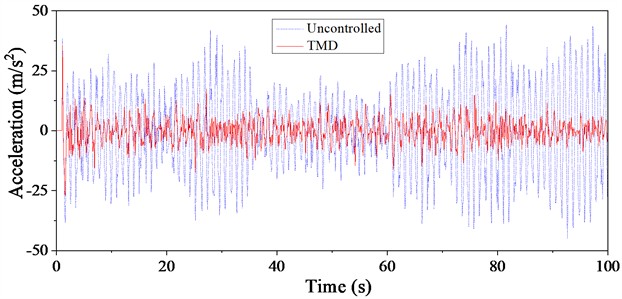
c) Basic wind speed: 40 m/s

Analyzing the vibration reduction mechanism of the TMD and the spectral characteristics of wind and rain loads provides insight into the observed effects. Pulsating wind and rain loads are inherently random, and the variability in the response induced by these random loads results in differing TMD performance. Long-period wind and rain loads effectively excite the first mode of vibration in the signal transmission tower structure, which aligns well with the TMD’s primary focus on controlling the first mode frequency. Therefore, the TMD demonstrates strong control capabilities for wind and rain-induced vibrations in tall structures. Additionally, from the trend of the curves, the root mean square (RMS) reduction ratio is more favorable compared to the peak reduction ratio. A quantitative analysis of the vibration reduction effect will be conducted in subsequent sections.

The displacement time history curves under wind and rain loads for the signal transmission tower, with and without TMD control, are compared in Fig. 16. Similar to the acceleration reduction effects, the TMD also demonstrates substantial potential for reducing displacement under wind and rain load excitation. The TMD's reduction effect on displacement follows a pattern consistent with its impact on acceleration, showing similar differences across various basic wind speeds. From the response at each time point, it is evident that the displacement response of the structure under TMD control is consistently smaller than that of the uncontrolled structure throughout the time period, highlighting the stable control capability of the TMD. Among the three basic wind speeds, the peak reduction in displacement under a basic wind speed of 30 m/s is the smallest, indicating a lower peak reduction ratio. In contrast, the TMD shows better peak displacement reduction under the other two basic wind speeds.

Analyzing the vibration reduction effects on displacement in conjunction with the TMD's vibration reduction mechanism, wind and rain loads are characterized by long periods and rich spectral content. These long-period loads effectively excite the primary vibration modes of the structure, leading to maximum responses that align well with the TMD's tuning advantages for vibration reduction.

It can be observed that under wind and rain loads, the displacement at the top of the structure primarily shifts in the positive X-direction. Fig. 17 illustrates the comparison of base shear time histories under wind and rain loads. It is evident that the base shear direction is exactly opposite to the displacement direction. The TMD effectively suppresses the wind and rain-induced vibrations at the top of the signal transmission tower. The response of the structure varies with different basic wind speeds, and consequently, the effectiveness of the TMD control also changes. Generally, the TMD performs better under wind and rain loads at basic wind speeds of 20 m/s and 40 m/s compared to a basic wind speed of 30 m/s.

From the perspective of load frequency spectrum characteristics, the wind and rain loads have a rich frequency spectrum and belong to long-period loads, exhibiting a certain degree of randomness. This variability in the excitation leads to differences in the structural response and, consequently, in the vibration reduction effectiveness of TMD. Additionally, the reduction in base shear under TMD control helps mitigate the interaction between the superstructure and the foundation, thereby reducing fatigue damage and ensuring safe operation.

Fig. 16Time history curve of top displacement of TV tower under wind-rain load

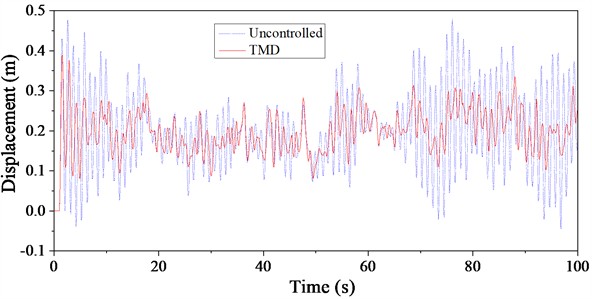
a) Basic wind speed: 20 m/s

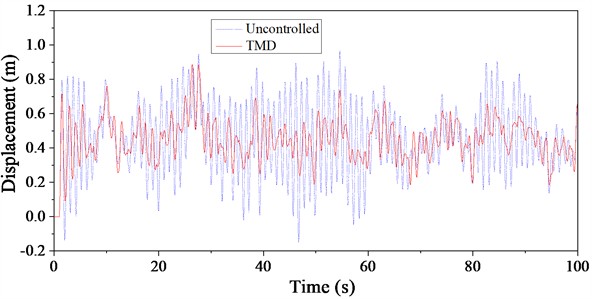
b) Basic wind speed: 30 m/s

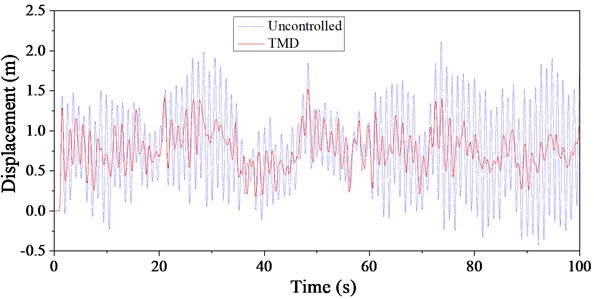
c) Basic wind speed: 40 m/s

Quantitative data on vibration reduction, including acceleration, displacement, and base shear response reduction ratios under wind and rain loads, are presented in Table 9. To illustrate with acceleration response as an example, the peak reduction ratios for basic wind speeds of 20 m/s and 30 m/s are quite similar, at 7.18 % and 7.24 %, respectively. In contrast, the peak reduction ratio is most effective at a basic wind speed of 40 m/s, with a reduction ratio of 21.22 %. The root mean square (RMS) reduction ratio better reflects the TMD's ability to control structural responses to wind and rain-induced vibrations. For basic wind speeds of 20 m/s and 30 m/s, the RMS reduction ratios of the top acceleration response are 64.67 % and 63.23 %, respectively. At a basic wind speed of 40 m/s, the RMS reduction ratio reaches 70.89 %, demonstrating the effectiveness of TMD in controlling wind and rain-induced vibrations.

Fig. 17Time history curve of base shear force of TV tower under wind-rain load

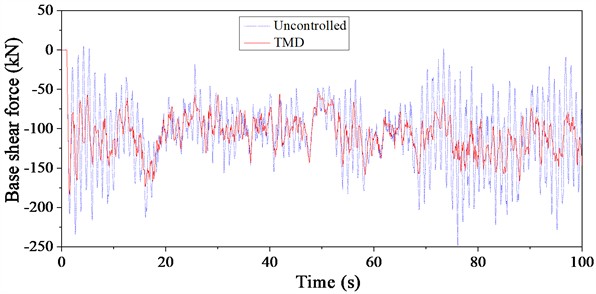
a) Basic wind speed: 20 m/s

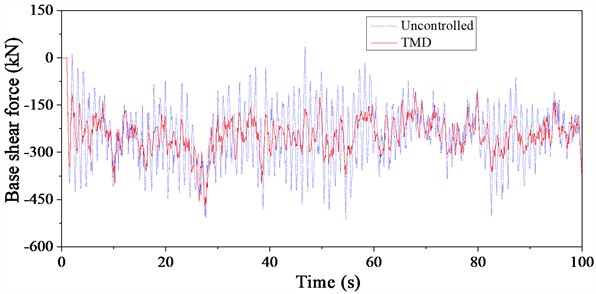
b) Basic wind speed: 30 m/s

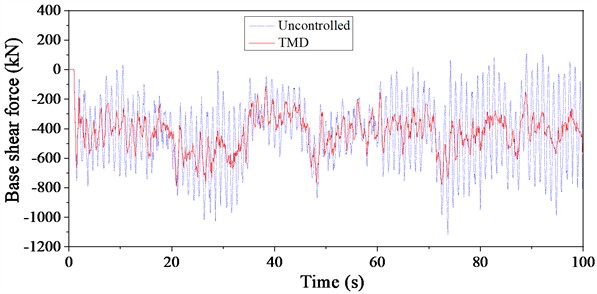
c) Basic wind speed: 40 m/s

Since the structure under wind and rain loads shifts primarily in the $X$-direction, resulting in displacement and base shear responses being skewed to one side of the coordinate axis, the RMS reduction ratio is less suitable for representing the control effectiveness of TMD in this context. However, the peak reduction ratios still clearly indicate a significant decrease in response with TMD control. The response time history curves shown in Fig. 12-14 provide a more intuitive depiction of the TMD’s effective control over wind and rain-induced vibrations.

4.3. Parameter analysis

The analysis of vibration control under wind and rain loads also considers the impact of mass ratio and frequency ratio on the TMD's vibration control capability. A parametric analysis is conducted to determine the optimal TMD control parameters, aiming to achieve the best control effect and effectively suppress undesirable vibrations of the signal transmission tower under wind and rain loads. Unless otherwise specified, the mass ratio is set at 2 %, and the frequency ratio is taken as 1.0$f_o$. Considering extreme rainfall conditions, wind loads with a basic wind speed of 20 m/s are used as input. The ratio of the peak displacement response at the top of the tower with TMD control to the peak displacement response without control is selected as the metric for evaluating the vibration control effectiveness of TMD.

The results of the parametric analysis of the mass ratio reveal the variation in the peak displacement response ratio with and without control, as shown in Fig. 18. Generally, as the mass ratio increases, the displacement ratio also increases, indicating that a larger TMD mass improves the reduction of the tower top displacement. The slope of the curve between mass ratios of 1 % and 1.5 % is steeper compared to the latter part of the curve. At 2 %, the slope shows a notable change; before this point, the increase in the TMD’s mass results in a more rapid improvement in vibration reduction. Beyond this point, the impact of the mass ratio on the TMD’s vibration reduction capability diminishes, with only a modest increase in reduction effect relative to the mass ratio.

The choice of control parameters is crucial for the TMD’s effectiveness. While a larger mass improves the vibration reduction effect, it also significantly affects the structure and can lead to cumulative damage. Considering both the enhancement in control and the potential impact on the structure, a mass ratio of 1.5 % is selected as the optimal for the TMD.

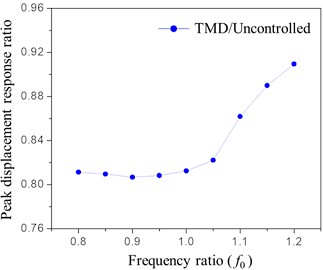
The parametric analysis of the frequency ratio shows the variation in peak displacement responses under different frequency ratios, as illustrated in Fig. 19. As the frequency ratio increases from 0.8 to 1.2, the displacement ratio initially decreases and then increases, indicating that the effectiveness of TMD in reducing tower top displacement first improves and then diminishes. When the frequency ratio is below 0.9, the displacement ratio decreases gradually, with a modest improvement in vibration reduction. However, when the frequency ratio exceeds 0.9, the reduction effect decreases noticeably.

The control frequency is a crucial parameter for the TMD and serves as the core of the tuned mass damper. The displacement ratio response curves for various frequency ratios under wind and rain loads remain below 1.0, demonstrating that the TMD performs well across the entire range of frequency ratios. The frequency ratio of 0.9 represents a significant turning point, where the TMD exhibits optimal control capabilities. Therefore, for wind and rain load conditions, a frequency ratio of 0.9 is selected as the optimal frequency ratio for the TMD.

Fig. 18Analysis of mass ratio under wind-rain load

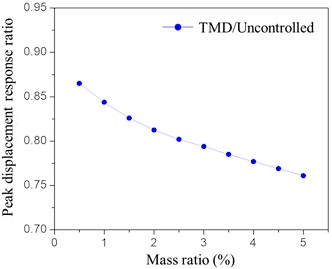
Fig. 19Analysis of frequency ratio under wind-rain load