Optimal parameters of tuned mass damper for the reduction of wind-induced vibration of high-rise buildings

2.1. Vibration of multi-degree-of-freedom system under wind excitation

The motion equation of the multi-degree-of-freedom (MDOF) system under wind excitation is given by:

where$\left[M\right]$, $\left[C\right]$ and $\left[K\right]$ are the mass, damping and stiffness matrix of the structure respectively;$\left\{\ddot{x}\right(t\left)\right\}$, $\left\{\dot{x}\right(t\left)\right\}$ and $\left\{x\right(t\left)\right\}$ are acceleration, velocity and displacement vectors respectively; $\left\{P\right(t\left)\right\}$ is the wind force vector; $w_0$ is the basic wind pressure; ${\mu }_{s_i}$ is the body shape coefficient at the $i$th particle; $\alpha$ is the ground roughness index; ${\mu }_R$ is the ground roughness correction coefficient. The surface roughness of class A to D is 1.284, 1.000, 0.544 and 0.262 according to related design codes of China, and $A_i$ is the windward surface area.

2.2. Vibration of MDOF system with TMD under wind excitation

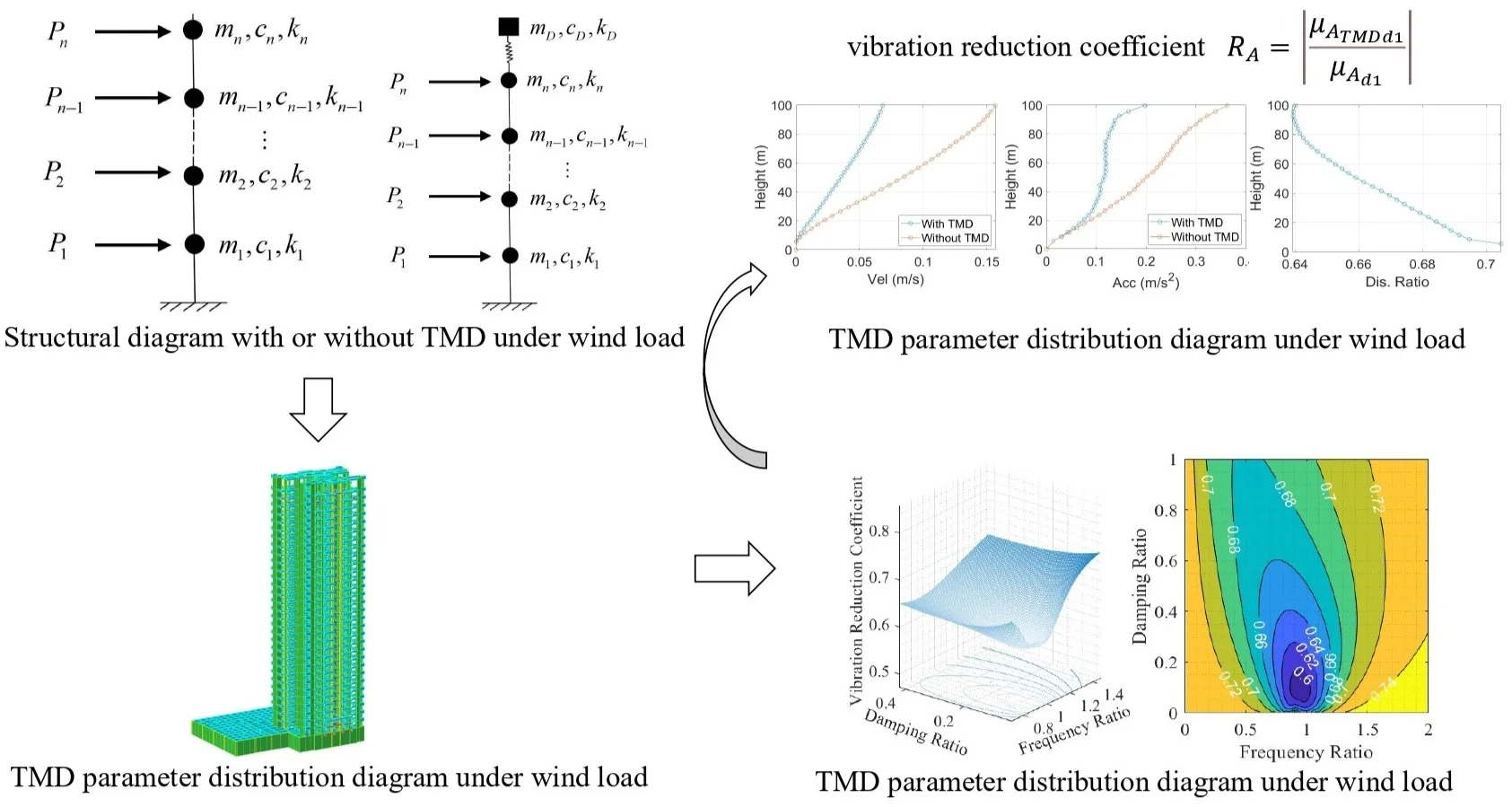
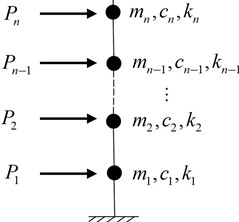
In this paper, TMD is used to reduce the vibration response of high-rise structures and installed on the top of high-rise buildings. The building structure is simplified into $n$ lumped masses, and its motion form under wind load is shown in Fig. 1.

Fig. 1Schematic diagram of structure with TMD under wind load

a) Simplified structural model without TMD

b) Simplified structural model with TMD

In order to facilitate subsequent analysis, considering that the structure is in linear elastic state, under the action of wind load $P\left(t\right)$, the motion equation of the high-rise structure with TMD can be expressed as:

where $M$, $C$ and $K$ are the mass matrix, damping matrix and stiffness matrix of the high-rise structure respectively. $x={[x_1,x_2,\dots ,x_n]}^T$, $\dot{x}={[{\dot{x}}_1,{\dot{x}}_2,\dots ,{\dot{x}}_n]}^T$, $\ddot{x}={[{\ddot{x}}_1,{\ddot{x}}_2,\dots ,{\ddot{x}}_n]}^T$ are respectively the displacement, velocity and acceleration of each lumped mass relative to the ground; $x_D$, ${\dot{x}}_D$ and ${\ddot{x}}_D$ are the displacement, velocity and acceleration of TMD relative to the top of the high-rise structure, respectively; $P\left(t\right)={[P_1\left(t\right),P_2\left(t\right),\dots ,P_n\left(t\right)]}^T$ is the excitation under wind load; $I={[\mathrm{0,0},\mathrm{}1]}^T$ is the position column vector of TMD.

In order to facilitate the modal decomposition of Eqs. (1) and (2), take $x={\mathrm{\Phi }}^{T}q$, $\dot{x}={\mathrm{\Phi }}^T\dot{q}$, $\ddot{x}={\mathrm{\Phi }}^T\ddot{q}$, where $\mathrm{\Phi }$ is the mode vector and $q$ is the generalized coordinate. Since the TMD system mainly controls the first mode of the structure, the first mode of the mode considered for Eq. (1) is as follows:

where $r={\mathrm{\Phi }}_1^{T}I/M_1^{*}$ and multiply both ends of the above equation right by ${\mathrm{\Phi }}_1$ at the same time, and divide by the generalized mass of the first mode $M_1^{*}={\mathrm{\Phi }}_1^{T}M{\mathrm{\Phi }}_1$:

In Eq. (6), ${\xi }_1={\mathrm{\Phi }}_1^{T}C{\mathrm{\Phi }}_1/2M_1^{*}{\omega }_1$ is the damping ratio of the first mode of the high-rise structure, and ${\omega }_1=\sqrt{{\mathrm{\Phi }}_1^{T}K{\mathrm{\Phi }}_1/M_1^{*}}$ is the frequency of the first mode. $P_1^{*}\left(t\right)$ is the generalized wind load of the first order mode, and $P_1^{*}\left(t\right)={\mathrm{\Phi }}_1^T{P}_i\left(t\right)$, where ${\mathrm{\Phi }}_{1i}$ is the mode shape component of the first order mode corresponding to the $i$th lumped mass, and $P_i\left(t\right)$ is the wind load corresponding to the $i$th lumped mass.

Similarly, the first mode vector is introduced to the right end of Eq. (4) ${\ddot{x}=\mathrm{\Phi }}_1^T{\ddot{q}}_1$ to obtain:

Assume that $\beta ={\mathrm{\Phi }}_1^{T}I$, and divide both ends of the Eq. (7) by $m_d$:

Then Fourier transform is performed on both ends of Eq. (6), and respectively $\mathcal{F}\left(q_1\right)=F_{q_1}\left(\omega \right)$, $\mathcal{F}\left({\dot{q}}_1\right)=\left(i\omega \right)F_{q_1}\left(\omega \right)$ and $\mathcal{F}\left({\ddot{q}}_1\right)={{\left(i\omega \right)}^{2}F}_{q_1}\left(\omega \right)$. Here $F_{P_1^{*}}\left(\omega \right)$ is the Fourier transform of the generalized force, the following equation is obtained:

The Fourier transform is also performed on both ends of Eq. (8), and the transformation relations $\mathcal{F}\left(x_D\right)=F_{x_D}\left(\omega \right)$, $\mathcal{F}\left({\dot{x}}_D\right)=\left(i\omega \right)F_{x_D}\left(\omega \right)$ and $\mathcal{F}\left({\ddot{x}}_D\right)={{\left(i\omega \right)}^{2}F}_{x_D}\left(\omega \right)$ are adopted. Then resulting equation is given by:

$F_{q_1}\left(\omega \right)$ and $F_{x_D}\left(\omega \right)$ can be solved by the combination of Eq. (9) and (10), where $F_{q_1}\left(\omega \right)$ is the Fourier spectrum of the vibration of the main structure of the high-rise structure, and $F_{x_D}\left(\omega \right)$ is the Fourier spectrum of the vibration of the TMD substructure.

Therefore, when considering the first mode of vibration of the TMD system under wind load, the power spectrum of the structure is as follows, where $C_1={\mathrm{\Phi }}_1^{T}C{\mathrm{\Phi }}_1$:

Similarly, under wind load $P\left(t\right)$, the motion equation of structure without TMD can be expressed as:

Assume that $x={\mathrm{\Phi }}^{T}q$, and similarly decompose Eq. (12) to obtain:

Then Fourier transformation is performed, and relations$\mathcal{F}\left(q_n\right)=H_{q_n}\left(\omega \right)$, $\mathcal{F}\left({\dot{q}}_n\right)={\left(i\omega \right)H}_{q_n}\left(\omega \right)$, $\mathcal{F}\left({\ddot{q}}_n\right)={{\left(i\omega \right)}^{2}H}_{q_n}\left(\omega \right)$ and $F\left(P_n^{*}\right(t\left)\right)=F_{P_n^{*}}\left(\omega \right)$ are adopted to obtain:

Therefore, the power spectrum of the structure without TMD is expressed as:

2.3. The amplitude of a random process with given power spectrum and the vibration-reduction coefficient

For a random process $s\left(t\right)$ with given power spectrum $G_s\left(w\right)$, its amplitude (maximum absolute value) $A$ satisfies the probability distribution density function as given in Eq. (16), and the amplitude $A$ can be calculated using Eq. (17) [4]:

where $a=s/\sqrt{{\lambda }_0}$, $\nu =\sqrt{{\lambda }_2/{\lambda }_0}/\pi$, $q_e=q^{1+b}$, $q=\sqrt{1-({\lambda }_1^2/{\lambda }_0{\lambda }_2})$, $b=0.2$, $f_A\left(s\right)$ is the probability density function of $A$, $d{F}_A\left(s\right)/ds=f_A\left(s\right)$.

For the random process corresponding to the power spectrum given by Eq. (11) and (15), we use the above equations to calculate the corresponding maximum absolute value ${\mu }_{A_{TMDd1}}$ and ${\mu }_{A_{d1}}$ respectively, according to which the vibration reduction coefficient $R_A$ can be calculated [5]:

$R_A$ (vibration reduction coefficient) is a function of mass ratio, frequency ratio and damping ratio. When its minimum value is achieved, it corresponds to the optimal frequency ratio and damping ratio of TMD.

3.1. Determination of TMD optimization parameters

For the case that the mass ratio is 0.05, the vibration reduction coefficient as a function of damping ration and frequency ratio is shown in Fig. 3(a), it can be seen that it presents a downward concave shape, which indicates the optimal solution for TMD parameters. Moreover, when the damping is relatively small and the frequency ratio is close to 1, it can be found that the vibration reduction coefficient will be greater than 1, which indicates that simply increasing the damping ratio cannot achieve better vibration reduction effect. It might actually cause larger vibration. As can be seen from the isoline of vibration reduction coefficient in Fig. 3(b), the same law exists. The closer the parameter is to the optimal one, the more obvious the vibration reduction effect will be. When the optimal parameters of TMD are obtained, the optimal damping ratio and the optimal frequency ratio are 0.100 and 0.96, respectively, and the corresponding vibration reduction coefficient is 0.6846.

Fig. 2High-rise building structure

Fig. 3TMD parameter distribution diagram under wind load

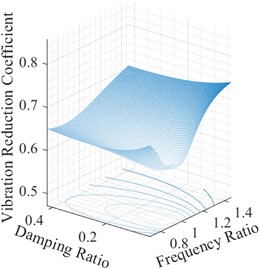
a) Three-dimensional diagram of vibration reduction coefficient

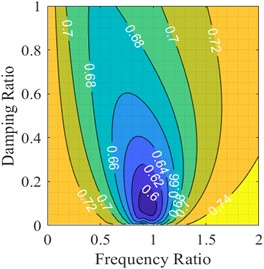
b) Isogram of vibration reduction coefficient

According to Table 1, when the mass ratio of TMD is changed, it can be seen from the four different mass ratios of 0.01, 0.03, 0.05 and 0.07 that the optimal damping ratio basically increases with the increase of the mass ratio, reaching the maximum value of 0.10 when the mass ratio is 0.05, and the optimal frequency ratio also reaches the maximum value of 0.96 when the mass ratio is 0.05. The results obtained were compared with those obtained by the classical optimization formulas such as J. P. Den Hartog and H. C. Tsai et al. [6]. Compared with the vibration reduction coefficient 0.7260 obtained by the classical optimization method, the vibration reduction coefficient obtained by the optimization method was lower, 0.6846, indicating better vibration reduction effect.

3.2. Analysis of the effect of the power method of TMD

In order to further understand the optimal parameters and vibration reduction performance of TMD, the optimal damping coefficient is obtained when the mass ratio is 0.05. Taking the controlled structure as an example, according to the conditions given in Eq. (2), 20 sets of wind load time-history data are generated, and the corresponding dynamic response of the structure is calculated by time-history analysis method. In Fig. 4, the average value of maximum displacement and maximum acceleration velocity of each layer of the structure under 20 groups of wind load input and the ratio of maximum displacement response of each layer before and after setting TMD are listed.

It can be seen from Fig. 4(a) that the maximum displacement along the height direction of the high-rise structure increases with the increase of height. The maximum displacement of the top of the structure without TMD and with TMD is 0.118 m and 0.075 m, respectively. When the optimal TMD parameters are adopted, the maximum displacement at the top of the high-rise structure decreases by 36.44 %. As can be seen from Fig. 4(b), the maximum acceleration is 0.20 m/s², and the maximum acceleration of non-TMD structure is 0.36 m/s², which decreases by 44.4 %. Fig. 4(c) shows that the damping effect of the top layer after TMD installation is 0.64 when TMD is not installed.

Fig. 4TMD parameter distribution diagram under wind load

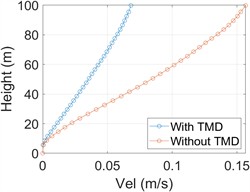
a) The maximum displacement along the height of the structure

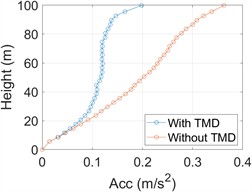
b) Maximum acceleration along the height of the structure

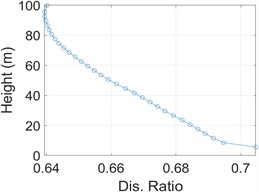
c) Column displacement ratio before and after TMD installation