Damage imaging in composite curved panels based on 2D wavelet analysis of guided wavefields

2.1. 2D CWT

If $f\left(\mathbf{x}\right)\in L^2\left(R^2\right)$is square-integrable, the 2D CWT can be defined as [15]:

where ‘*’ represents the complex conjugate; ${\psi }_{\mathbf{u},s,\theta }\left(\mathbf{x}\right)$ denotes the shifted, scaled, and rotated version of 2D mother wavelet and is expressed as:

where $\mathbf{u}=(u_x,u_y)$ is the translation vector; $s$ is the scale factor; $r_{-\theta }$ is a 2D rotation matrix as:

The expression of Eq. (1) in the Fourier domain is:

where ‘^’ denotes the Fourier transform operator and $\mathbf{\omega }$ is the spatial frequency vector.

The mother wavelet used in this research is a 2D Morlet wavelet, which is defined in the frequency domain as:

2.2. 2D CWT wavefields

The structure studied in this research is a cylindrical curved panel, as shown in Fig. 1: $\gamma$ is the inner radius, $d$ is the thickness, $\alpha$ is the angle crossed by the curved edge of the panel, $W$ is the arc length, and $L$ is the length of the straight edge. The wavefield signal is the radial displacement field on the panel surface and is denoted as $v\left(\mathbf{x},t\right)$, where $t\in \left[0,T\right]$ is the time of wave propagation.

Fig. 1Schematic diagram of the curved panel

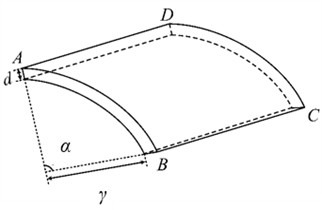
a) Stereoscopic view

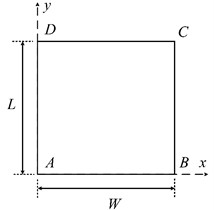
b) Plane view

In accordance to Eq. (1), the 2D CWT wavefield is obtained as:

To consider signal features in different propagating directions, the 2D CWT-wavefield is fused in the rotation angle domain as:

where $W_{\theta }(\mathbf{u},s,t)$ is called overall 2D CWT wavefield. In this study, rotation angles are taken from 0 to 15$\pi$/8 in an increment $\pi$/8.

2.3. Damage imaging based on 2D CWT wavefields

A wavefield energy time distribution function is defined as:

As the wave is excited and propagates in the panel, $E_t$ increases from zero to its maximum value (denoted as $t_0$ at this time), and then maintains a stable state if there is no energy dissipation. At the stage where $E_t$ increases from zero to its maximum value, the wavefield signal is mainly concentrated around the excitation point and is not suitable for damage imaging. Therefore, in this research, the overall 2D CWT wavefields within the time window after $E_t$ reaches its maximum value are fused by calculating the energy map as:

Damage can be visualized in the overall 2D CWT wavefield energy map.

3.1. Sample description

Fig. 2 shows the schematic diagram of the simulated curved panel with single delamination. The parameters used in the simulation are as follows: $L$ is 400 mm, $d$ is 2 mm, $\alpha$ is 57.3°, $\gamma$ is 400 mm. The specimen is composed of eight layers, with a thickness of 0.25 mm for each layer. The stacking sequence of these layers is [0°/90°/90°/0°]_s. The delamination is located between the second and third layers from the top to the bottom surface, and its in-plane position is shown in Fig. 2, with a size of 30×30 mm². The finite element model is shown in Fig. 3 with a total of 204800 elements and an element type of SC8R. The boundary condition of the curved panel is set as a free boundary constraint. Material properties of the composite curved panel are shown in Table 1. A 5-cycle sine pulse excitation signal with a central frequency of 50 kHz modulated by a Hann window is applied to the central node of the bottom panel surface. Upon the application of the excitation, 100 frames of radial displacement of each node on the top panel surface are collected, forming a continuous 1.5 ms radial displacement wavefield.

Fig. 2Schematic diagram of a CFRP curved panel with single delamination

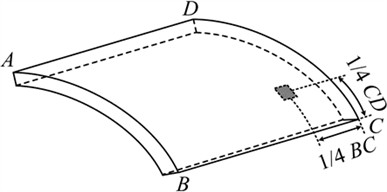
Fig. 3Finite element model of the composite curved panel

3.2. Results

Fig. 4 shows a comparison between the original wavefield images and the overall 2D CWT wavefield images at some time, with the original wavefield on the left and the overall 2D CWT wavefield on the right. When $t=$ 0.12 ms, the collision between waves and delamination generates small singular components. It is difficult to directly identify delamination from the original wavefield. However, the overall 2D CWT wavefield effectively amplifies the small singular components of the wavefield at the location of delamination. When $t=$ 1.02 ms, the singular components of the wavefield caused by delamination are submerged in the principal wavefield components, but they are clearly presented in the overall 2D CWT wavefield.

Fig. 4Wavefield images and overall 2D CWT wavefield images

a)$t=$ 0.12 ms

b)$t=$ 1.02 ms

A 2D CWT wavefield image at a specific moment can achieve damage localization, but it is difficult to accurately determine the size and shape of the damage. Fig. 5(a) and (b) show the overall 2D CWT wavefield energy maps respectively formed by non-windowed and windowed fusion of the overall 2D CWT wavefields. From Fig. 5, it can be seen that accurate imaging of delamination has been achieved through image fusion. In Fig. 5(a), there is an energy concentration phenomenon at the excitation location, while in Fig. 5(b), it can be seen that energy concentration at the excitation location is eliminated through windowed fusion.

Fig. 5Overall 2D CWT wavefield energy maps

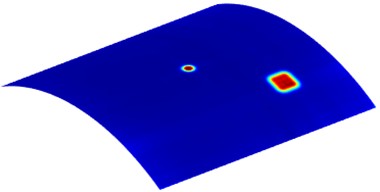
a) Non-windowed fusion

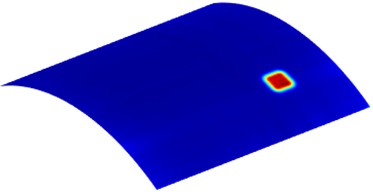
b) Windowed fusion