Interaction of pipelines with landslides: analysis of mechanical properties at different strengths

1. Introduction

As one of the most destructive natural disasters, landslides seriously affect the safety of human life and property, and cause serious damage to the social environment and infrastructure [1]. With the development of China's socio-economic landscape and the increasing demand for infrastructure construction, the construction of long-distance pipelines inevitably traverses regions prone to landslides. As one of the countries most severely affected by landslide disasters, China frequently experiences pipeline deformation or damage due to landslides, significantly impacting their normal operation. For example, in December 2015, the catastrophic landslide resulting from a dam collapse in Shenzhen, Guangdong, caused pipeline ruptures due to the immense impact force of the landslide mass. This led to massive natural gas leaks, significant casualties, and a disruption in gas supply to Hong Kong. Similarly, in July 2016, continuous heavy rain in Enshi, Hubei Province, triggered a landslide that ruptured the “West-East Gas Pipeline”, causing gas leaks and subsequent explosions. Furthermore, the China-Myanmar natural gas pipeline in Qinglong, Guizhou Province, experienced two pipeline rupture incidents due to landslides in 2017 and 2018, resulting in substantial economic losses.

Currently, research on landslide geological hazards in loess regions within China is quite extensive [2]. However, the study of the interaction between landslides and pipelines remains insufficient. Although some scholars have started to focus on and investigate the interaction between pipelines and landslides, most research is still based on theoretical experience and analytical derivations. In numerical simulation analysis, the primary method used is the Finite Element Method (FEM). Huang et al. [3] used FEM to simulate the seismic response of slopes under different groundwater levels, accounting for the unsaturated state of the soil and the earthquake-induced excess pore water pressure. Additionally, in 2023, they proposed a new theory for the seismic stability analysis of unsaturated slopes and simulated the failure process of slopes under seismic action [4]. Zhang et al. [5] proposed simulating soil-pipeline interaction using equivalent boundary springs and predicted pipeline displacement and strain under horizontal landslide action through FEM. International scholars have also conducted extensive research in geotechnical engineering using FEM. For instance, Das [6] and Biniyaz [7] conducted coupled analyses of multi-hazard slope stability using finite element analysis platforms. However, when dealing with complex terrains and large-scale problems, the FEM may encounter issues such as mesh distortion, reduced accuracy, difficulty in handling boundary conditions, and high computational costs due to the need for mesh division. These issues can limit its application in landslide analysis to some extent [8].

In contrast, the Smoothed Particle Hydrodynamics (SPH) method employs a Lagrangian coordinate system and, as a mesh-free method, effectively avoids computational errors caused by mesh distortion when handling complex interface problems. Due to its suitability for large deformation and free surface flow problems, the SPH method has increasingly been applied to various fluid-structure interaction numerical simulations, becoming a hotspot in geotechnical and hydraulic engineering research and achieving significant results. Hu et al. [9] in 2021 used the DEM-SPH method to simulate and predict the entire process of disaster chains such as landslides, providing important insights for the prevention of reservoir bank slope disasters. Huang et al. [10] in 2023 proposed a new DEM-SPH computational framework, simulating the liquefaction process of seabed soil under the combined action of tsunamis and earthquakes. However, literature on the use of SPH methods to study the interaction between landslides and pipelines remains scarce. Internationally, Baek [11] proposed L-RK and SL-RK approximate deformation-related coupling content, emphasizing the performance of mesh-free methods in landslide modeling.

In this context, this study utilizes the open-source DualSPHysics code library to conduct simulation research. DualSPHysics is not only capable of simulating a wide range of complex fluid dynamics problems, such as free surface flows, waves, collisions, and liquid-solid-gas interactions, but it can also couple with other physical models, such as the Discrete Element Method (DEM) and the Finite Element Method (FEM), to address multiphysics coupling problems [12]. Additionally, it supports parallel processing on CPUs or GPUs, significantly enhancing its capability to solve real-world engineering problems, and has been widely applied in engineering and scientific research fields [13], although relatively few researchers use this software. In 2019, Jiang et al. [14] utilized the multiphase flow model of DualSPHysics to analyze the maximum surge wave height generated by landslides. Ma et al. [15] in 2024 proposed a new bidirectional coupling method to study the entire disaster chain of mountain reservoirs, simulating the movement of landslides and fluids. However, simulation and analysis of the interaction between landslides and pipelines remain insufficient. Therefore, the primary objective of this study is to implement numerical simulations of landslide hazards and pipelines based on the DualSPHysics open-source code library. This research aims to investigate the mechanical response of pipelines to mountain landslide hazards under various conditions and to further analyze the interaction mechanisms between landslides and pipelines. The findings of this study will provide valuable references for the preliminary site selection, construction, maintenance, and hazard inspection of pipeline projects.

2. Method

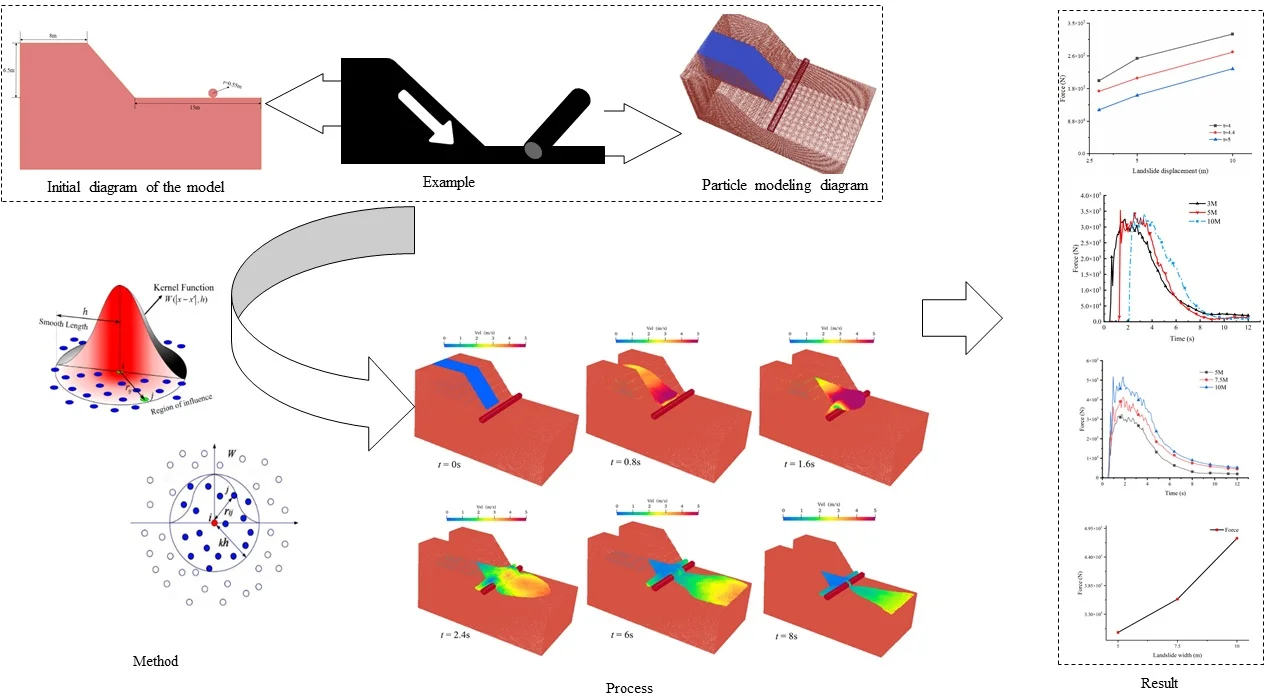
The Smoothed Particle Hydrodynamics (SPH) method was proposed to address problems in fluid dynamics. Essentially, it approximates the problem domain using a series of particles with physical properties. These particles can reconstruct equations through kernel approximation. The initial expression of the kernel approximation in the SPH method is defined as shown in Eq. (1) [16]:

where $f\left(r\right)$ represents the physical quantity of the particle at position $r$, $W(\left|r-r\text{'}\right|,h)$ is referred to as the interpolation kernel function or simply the kernel function, $r-r\text{'}$ is the distance between particles, and $h$ is the smoothing length that defines the influence radius of 𝑊.

The smoothing kernel function must also be an even function, with its integral over the entire region equal to 1, satisfying the normalization condition. Additionally, as the smoothing length approaches zero, the kernel function should exhibit the properties of the Dirac delta function. The mathematical form is shown in Eq. (2):

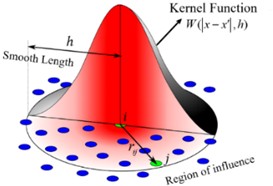
The particle approximation provides a numerical method for solving equations, allowing continuous integral problems to be transformed into a discrete summation over all particles. The particle approximation equation is shown in Eq. (3). Fig. 1 illustrates the kernel approximation and the particle approximation process of the SPH method:

where $m_j$ is the mass of particle $j$, ${\rho }_j$ denotes the density of particle $j$$(j=\mathrm{1,2},3,\cdots ,N)$, and $N$ indicates the number of particles within the domain.

Fig. 1Schematic diagram of the SPH algorithm

a) SPH smooth kernel function approximation

b) SPH particle approximation

The smoothing kernel function plays a crucial role in the computation process of the SPH method and is a key factor affecting the accuracy of the results. And the Wendland kernel function is employed:

where $q=\left|r_i-r_j\right|/h$ is the particle spacing, ${\alpha }_D$ equals $21/\left(16\pi h^3\right)$ in 3D and $7/\left(4\pi h^2\right)$ in 2D. Subsequently, the classical Navier-Stokes equations in fluid dynamics are used for calculations [15]:

where $\mathbf{v}$ is the velocity vector, $\sigma$ is the pressure tensor, $\alpha$ and $\beta$ represent the coordinate directions, $g$ is the gravitational acceleration. The relationship between pressure and fluid particle density is approximated using the equation of state given by Eq. (7), where $\gamma =7$, ${\rho }_0$ is the reference density of the fluid particles and $c_0$ is the speed of sound:

3. Models

3.1. Initial step

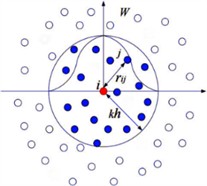
This study simulates a landslide under three-dimensional conditions, then adjusts the scale of the landslide and some parameters for comparative analysis. The initial landslide-pipeline model has a slope length of 15 meters, a slope angle of approximately 45°, a landslide height of 6.5 meters, a width of 5 meters, a particle spacing of 0.2 meters, and an approximate landslide volume of 350 cubic meters. The pipeline has a radius of about 0.55 meters and a length of 15 meters. In the numerical simulation, the gravitational acceleration is 9.81 m/s², and the model’s runtime is 12 s. The simplified landslide-pipeline model and the pipeline material parameters used in this study are as follows.

Fig. 2Initial diagram of the model

Table 1Steep pipe materials parameters

Name	Young modulus	Poisson ratio	Restitution coefficient	Kfric
X70	210Gpa	0.35	0.8	0.35

3.2. Algorithm simulation

In the SPH numerical simulation analysis, several models with different particle influence radius were constructed to select the appropriate particle density and artificial viscosity, and to determine their impact on the analysis results. Considering suitable computation time and practical effects, a particle spacing $d_p$ of 0.15 meters and an artificial viscosity value of 0.3 were ultimately chosen. The generated particle model is shown in Fig. 3. Next in the landslide-pipeline simulation, the process of visualizing the landslide on the pipeline can be clearly seen as shown in Fig. 4.

Fig. 3SPH particle modeling diagram

Fig. 4Schematic of simulation process

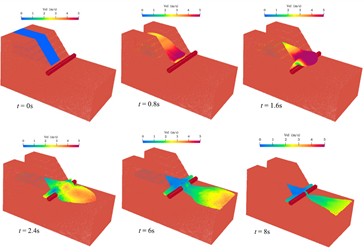
4. Analysis of results

To investigate the effects of different landslide conditions on pipelines, we modified the landslide displacement distance and the landslide body width based on the initial model while keeping other parameters constant. The landslide displacement distances were set at 3 meters, 5 meters, and 10 meters; the widths of the landslide body were set at 5 meters, 7.5 meters, and 10 meters. To better analyze the impact of these two factors on pipelines, we plotted curves depicting the relationship between pipeline stress and landslide displacement distance, and pipeline stress and landslide body width. The relationship between pipeline stress and landslide displacement is shown in Fig. 5, and the relationship with landslide body width is shown in Fig. 6.

Fig. 5Relationship between pipe forces and landslide displacements

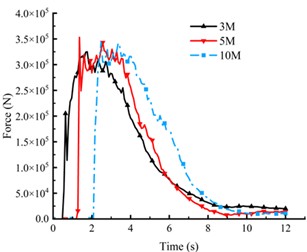
a) Total process of pipe force and landslide displacement

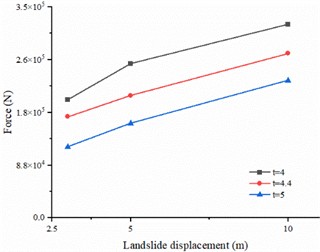
b) Pipe forces for different landslide displacement

From Fig. 5(a), it can be observed that as the landslide displacement increases, the onset time of the landslide’s impact on the pipeline is delayed. Additionally, the rate of increase in pipeline stress slightly accelerates, and after reaching a certain point, the rate of decrease also accelerates. This phenomenon may be attributed to the energy dissipation and structural changes in the landslide mass during its movement, resulting in a gradual reduction of the compressive and impact forces on the pipeline. In Fig. 5(b), it is observed that once the landslide starts to contact the pipeline, the stress on the pipeline continuously increases with the increase in landslide displacement. This is because the compressive and impact forces from the landslide on the pipeline intensify with increasing displacement, leading to greater stress on the pipeline. From the overall results of Fig. 6, it can be seen that as the width of the landslide mass increases, its volume also becomes larger, thereby generating greater compressive and impact forces.

Fig. 6Relationship between pipe forces and landslide width

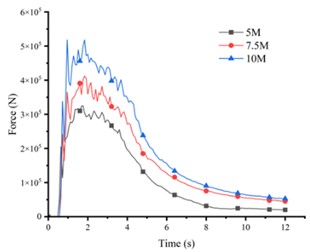
a) Pipeline force for three landslide widths

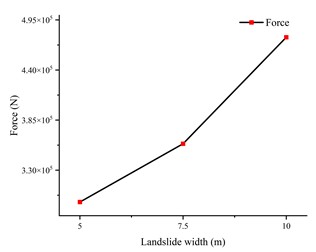
b) Pipe forces for different landslide widths

5. Conclusions

In this study, the SPH method was successfully utilized to simulate the entire process of soil particle erosion and encirclement around a pipeline. The dynamic process of landslide soil action on pipelines was visualized using GPU parallel accelerated computations via the Dualsphysics. Through in-depth analysis, the following main conclusions were drawn:

1) In the SPH method, the influence radius of different particles significantly affects the simulation results. Specifically, a smaller $d_p$ setting yields more accurate results but increases the complexity and computational load, thereby affecting simulation time and computational efficiency. Therefore, in practical applications, the influence radius size should be chosen reasonably based on specific research needs and available computational resources.

2) Landslide displacement has a significant impact on pipeline stress. Experimental results indicate that as landslide displacement increases, the force exerted on the pipeline also increases, and the rate of change in pipeline stress accelerates. This finding is crucial for assessing the impact of landslides on pipeline safety. Particularly in landslide-prone areas, pipeline design and maintenance must fully consider the influence of landslide displacement on pipeline stress.

3) The width of the landslide body has a more pronounced effect on pipeline stress. In the three different landslide body width models established in this study, it was found that pipeline stress is positively correlated with landslide body width. That is, the wider the landslide body, the greater the force exerted on the pipeline. This phenomenon is very close to the measured results of the pipeline-soil model established using the FEM in the published paper [17]. By comparing with the results of existing literature, the rationality and accuracy of the simulation results in this paper can be verified, which provides a scientific basis for landslide disaster prevention and pipeline safety protection.