Dynamic characteristic analysis and strength optimization of vibrating screen based on computer simulation technology

2.1. Model establishment

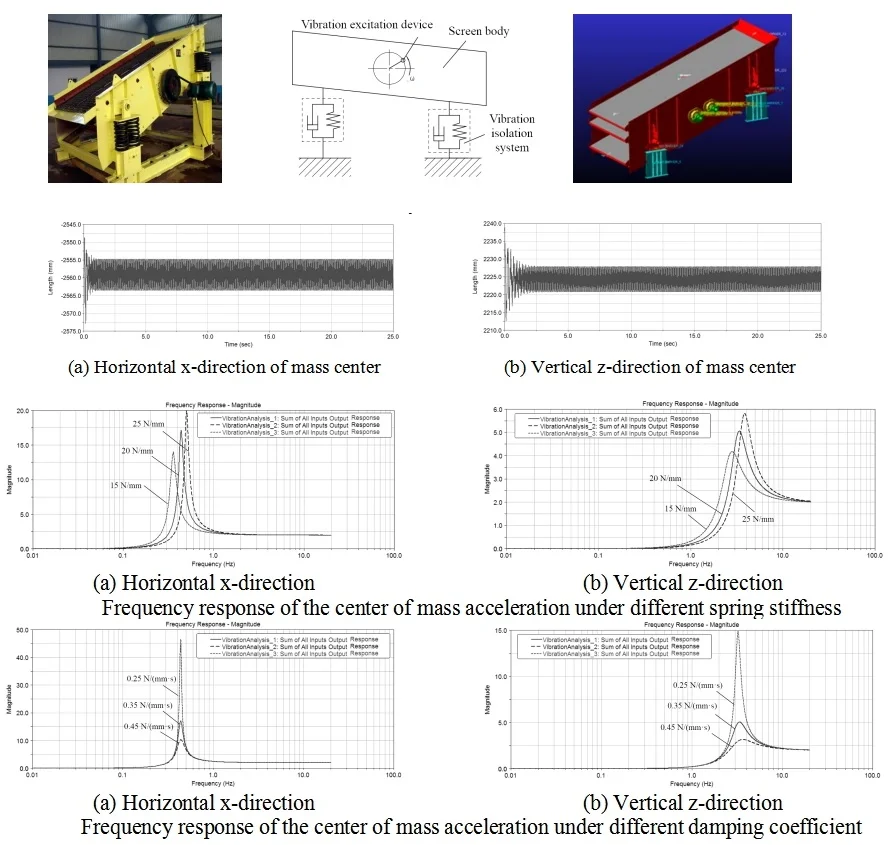
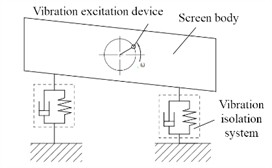
Vibration screening equipment, as shown in Fig. 1(a), mainly consists of three parts: excitation vibration device, screen body, and isolation system, as shown in Fig. 1(b). The excitation device generates periodic inertia excitation force, which enables the screen to continuously undergo periodic vibration. The screen body undergoes periodic motion due to the inertial excitation force generated by the vibration device, carrying the flow of animal material and passing through the screen to complete the screening process. The main function of the isolation system is to support the vibrating screen body and screen material, so that the screen body can vibrate at a specific amplitude and reduce the dynamic load transmitted to the foundation or structural support. Dynamics analysis is mainly used to study the motion of vibration systems under external loads. By establishing a dynamic model of the vibrating screen, the motion law of the vibrating screen in a stable motion state can be obtained. Export the 3D model created and assembled in SolidWorks to the parasolid file format. Import the exported file into ADAMS, set the gravity in the working environment in ADAMS/view, connect the components using Boolean operations, and set the density of each component based on its material properties. According to the actual operation of the vibrating screen, set constraint pairs on the simulation model in the constraint interface, as shown in Fig. 1(c). A fixed pair is set between each support seat of the vibrating screen and the ground, and a rotating pair is set between the excitation shaft and the bearing seat. A single row cylindrical roller bearing is installed at the corresponding position between the excitation shaft and the bearing seat, connected by a bearing between the excitation shaft and the bearing seat. A synchronous device is installed on one side of the excitation shaft for forced synchronization. Therefore, a synchronous belt and a synchronous wheel are set up, and the synchronous wheel is connected to one side of the excitation shaft.

Fig. 1Model and setting of hydraulic support

a) Assembly structure

b) Degree of freedom setting

c) Model

2.2. Dynamic characteristics analysis of mass center

Set the simulation time to 25 seconds and iterate the calculation steps to 10000. After the simulation calculation is completed, the dynamic data of the vibrating screen can be exported and processed accordingly through the ADAMS post-processing module. Fig. 2 shows the variation law of displacement over time in the vertical y-direction and horizontal $x$-direction at the center of mass of the vibrating screen body.

Fig. 2The motion law of the center of mass

a) Horizontal $x$-direction of mass center

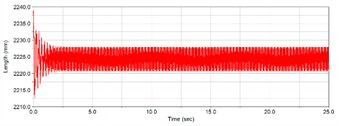
b) Vertical $z$-direction of mass center

According to the simulation results, it can be seen that the displacement change of the vibrating screen is relatively large during the start-up stage. This is because the vibrating screen is subjected to the combined action of free vibration and forced vibration during this stage, and the amplitude changes dramatically. After running for a period of time, the motion of the vibrating screen gradually stabilizes, and the $x$-direction and $z$-direction displacements show obvious periodic changes. Due to the gradual attenuation of free vibration with the operation of the vibrating screen until it reaches zero, the vibrating screen is only subjected to forced vibration during stable operation. During the start-up phase of the vibrating screen, the amplitude in the $z$-direction is greater than that in the $x$ direction. This is due to the fact that the vertical stiffness and damping coefficients of the vibrating screen rubber spring are greater than those in the horizontal direction.

2.3. Vibration response analysis of isolation system

The isolation system of the vibrating screen includes an upper support seat, a lower support seat, and a rubber spring. By simplifying the rubber spring into a spring and damping unit, the spectral response results of the center of mass acceleration under different spring stiffness and damping coefficient conditions can be obtained, as shown in Fig. 3 and Fig. 4.

Fig. 3Frequency response of the center of mass acceleration under different spring stiffness

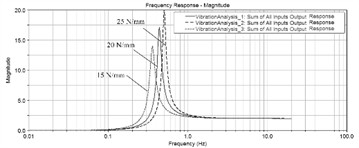
a) Horizontal $x$-direction

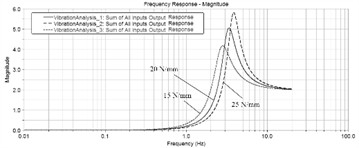
b) Vertical $z$-direction

Fig. 4Frequency response of the center of mass acceleration under different damping coefficient

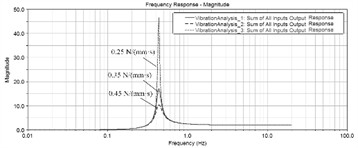
a) Horizontal $x$-direction

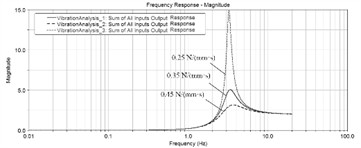
b) Vertical $z$-direction

It can be seen that the spring stiffness can significantly affect the natural frequency and vibration amplitude of the entire vibrating screen. Within a certain range, the higher the spring stiffness, the higher the natural frequency, and the corresponding amplitude. The damping coefficient does not affect the natural frequency of the system, but it greatly reduces the amplitude under resonance conditions. Rubber spring is an elastic component of damping support device, which achieves spring, vibration reduction and isolation effects through the elastic deformation of rubber. Rubber springs have good damping, sound insulation, and wear resistance, with a small elastic modulus and excellent nonlinear characteristics. They can withstand strong impact loads, absorb high-frequency vibrations and noise well, are easy to install and disassemble, and can withstand compression and shear deformation. Although the stiffness of rubber springs can meet the normal operation requirements of vibration screening equipment, their high damping characteristics can significantly attenuate the dynamic amplification factor of the system, and once produced and formed, it is difficult to fine tune the stiffness and damping. Under long-term exposure to high dynamic loads, aging, relaxation, and bulging phenomena are prone to occur, affecting work efficiency and screening effectiveness. When there is a significant height or stiffness difference between rubber springs, the vibrating screen may even exhibit lateral motion, affecting the normal operation of the equipment and the stability of the vibration system. When the vibrating screen undergoes periodic vertical downward vibration, the excitation force will be greater than the weight of the vibrating screen, and the upper support seat and rubber spring will periodically detach and collide, resulting in noise.

2.4. Modal analysis of screen body

In order to obtain the dynamic characteristics of the screen body, modal analysis is required. The finite element analysis model of the vibrating screen body is established, and the required modal vibration mode solving parameters are set. The Subspace method is used for modal solving operations. Under actual constraints, extract the first 6 modes of the vibrating screen after the calculation is completed as shown in Fig. 5 and Table 1. It can be seen that under the first order fixed frequency condition, the screen body begins to undergo bending deformation, and the maximum vibration displacement is located at the center of the two side clamping plates, which is related to the structural stiffness. At the second and third natural frequencies, the maximum amplitude is distributed on the supporting rod at the edge. The most significant deformation structure in the remaining modal shapes of the vibrating screen is the reverse twisting of the discharge end along the $z$-axis, followed by the serpentine twisting around the exciter along the $x$-axis. The main reason for this vibration pattern is that the stiffness of the discharge port is too small and the structure is not reasonable enough. In addition, the distribution of reinforced angle steel on the side plate is uneven.

Fig. 5The first six modal shapes

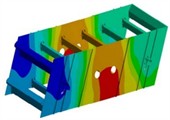
a) The first order

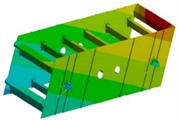
b) The second order

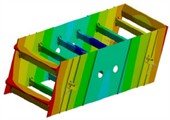
c) The third order

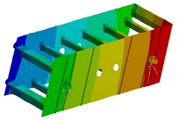
d) The fourth order

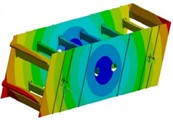
e) The fifth order

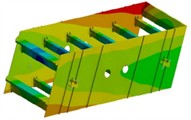
f) The sixth order

3.1. Strength analysis under ultimate load

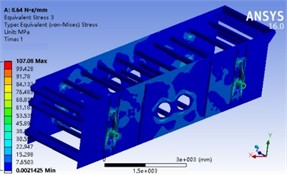
The quality of the grid directly affects the speed and accuracy of simulation solutions. Due to the large size and numerous components of the vibrating screen, automatic mesh division was first used to partition the entire machine. Structures that are prone to damage are subjected to mesh refinement, while other parts maintain the size of the automatically partitioned mesh, as shown in Fig. 6. The method of local refinement can ensure the accuracy of simulation results, reduce simulation computational complexity, and improve computational efficiency. The distribution of stress is shown in Fig. 7. It can be seen that the stress on the screen body is mainly concentrated on the supporting beams and the side plates near the excitation device. The stress at the connection between the supporting tube and the reinforcing rib of the supporting beam is the highest, with a maximum value of 107.08 MPa. As the supporting beam is a supporting structure connecting the screen box and the damping support device, it not only bears the mass of the screen body and the material during operation, but also the dynamic load composed of the excitation force generated by the excitation device and the inertia force of the screen body, which is transmitted to the damping support device, resulting in a high stress on the supporting beam.

Fig. 6Finite element mesh division results

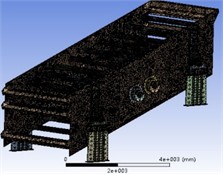
Fig. 7Overall stress field cloud map

3.2. Discussion on optimization schemes

According to the simulation analysis of the stress and modal vibration mode of the vibrating screen, it is known that the stress of the vibrating screen body is relatively high at the position of the support beam and the side plate near the excitation device, and the maximum stress of the support beam is close to the allowable stress. After long-term use, structural damage may occur, and the deformation of the two crossbeams near the lower excitation device and the side plate near the excitation device is relatively large. There is a certain problem of uneven structural distribution in the side plate of the vibrating screen. Therefore, on the basis of improving stress, a certain degree of lightweight improvement is proposed for the vibrating screen. In order to improve the stiffness and strength of the vibrating screen mechanical structure without increasing the manufacturing cost, the maximum value of the first-order natural frequency is set as the optimization target, and the minimum value of the mass and the minimum value of the stress peak are defined as the boundary conditions.

Fig. 8Structural parameters of design variables

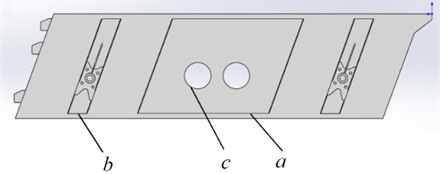
Fig. 9Optimized stress cloud map

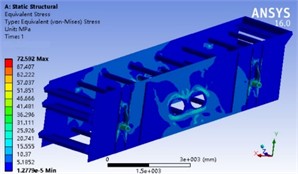
To enhance the structural strength of the side plate exciter position, improve stress distribution, and reduce deformation, the strengthening plate length $a$, rib spacing $b$, and pulley aperture $c$ are used as design variables, as shown in Fig. 8. For optimization algorithms, the response surface function method is chosen. Based on the characteristics of the design variables, the Latin hypercube DOE method was used to generate sample points, with a total of 15 points sampled to achieve approximate model fitting. Optimization is based on a model constructed with limited sample points, so the characteristic of this method is that the optimization time is fast, but it sacrifices some accuracy, which can be compensated for through secondary validation. According to engineering practice, the response function of stress has significant complex nonlinear characteristics. By fitting the regression function in the text and combining it with advanced optimization algorithms, the maximum target variable within the design variable range can be efficiently searched. Essentially, the optimization of separation performance is achieved through mathematical calculations to optimize parameter allocation and obtain the minimum stress peak and mass. The search for target extremum belongs to a typical iterative algorithm. To improve the stability of the calculation process and achieve global convergence, the total sample size can be defined first, and then the linear search factor can be combined with the Lagrangian value function to obtain a reasonable iteration step size. In the self adjustment of convergence speed, it is necessary to change the iteration step size according to the accuracy judgment criteria. Through continuous iterative calculations, the results of the design variables and optimization objectives can be obtained as shown in Table 2, and the optimized stress cloud map is shown in Fig. 9. It can be seen that on the premise that the mass remains basically unchanged, the maximum stress value can be decreased from 107.08 MPa to 72.59 MPa, with a reduction rate of 32.2 %. The first natural frequency has slightly increased. Compared with the stress distribution of the sieve body before improvement, the stress distribution is roughly the same, but the maximum stress value of the vibrating sieve body has been effectively reduced, indicating that the stress concentration of the structure can be effectively reduced, the stiffness can be improved, and there is sufficient redundancy with the allowable stress, which can be used for long-term operation. This indicates that the structural improvement scheme is very effective.