Abstract
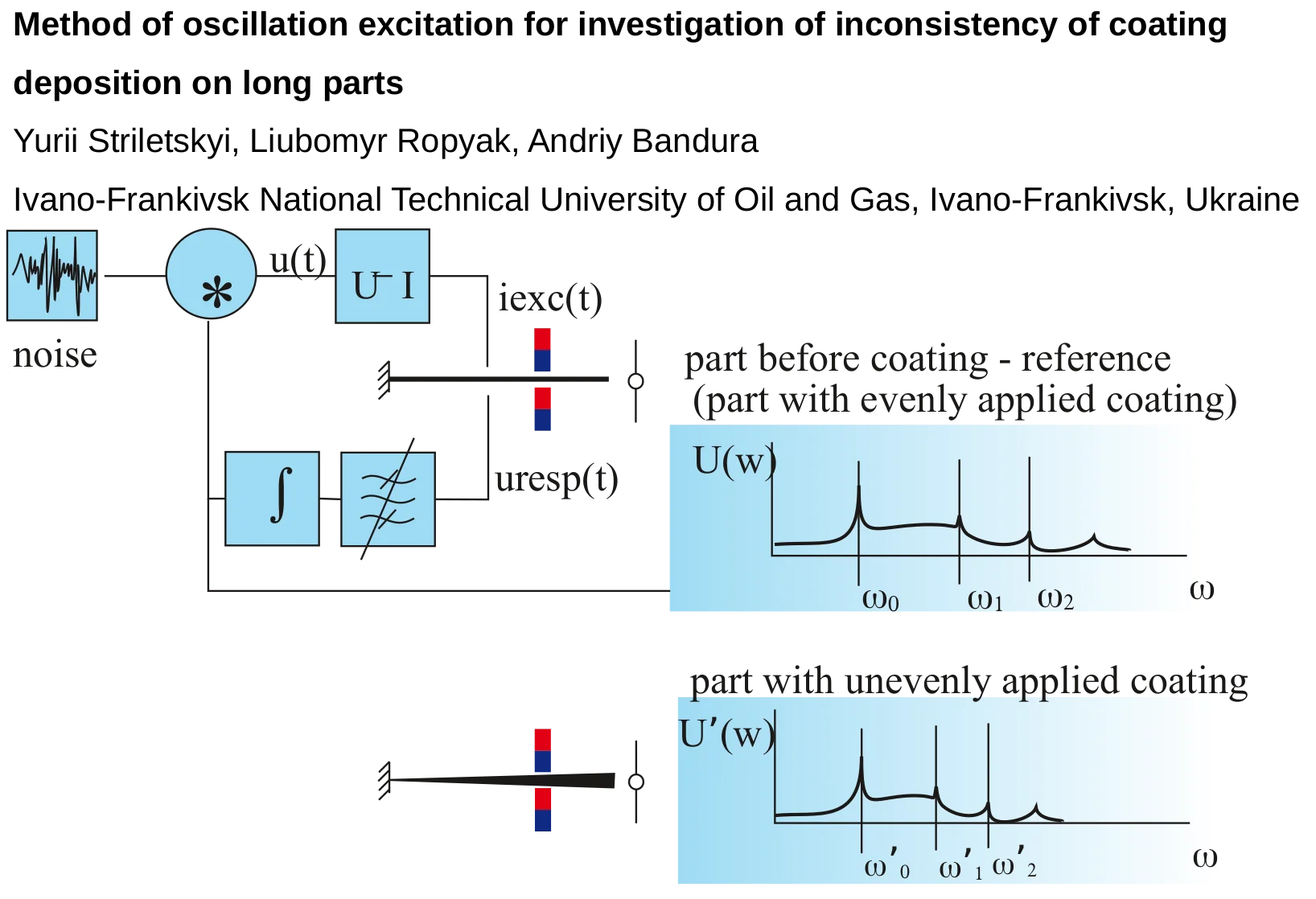
A method is proposed for studying the uniformity of electrochemical coating on the outer wall of a thin metal rod by determining the parameters of natural oscillations of this rod, which is clamped on one side. The parameters are studied by analyzing the natural frequencies of the rod. The uneven coating of the rod wall causes a change in the frequency of transverse modes and the shape of the bending line of the rod axis. The mechanical vibrations of the rod are excited by the interaction of an external magnetic field with the Ampere force arising from the current flowing through the rod. A method of adaptive tuning of the spectral components of the excitation current is developed by modifying the coefficients of a digital filter through which a noise-like signal pass. The coefficients of the digital filter are changed adaptively, based on the analysis of the signal spectrum obtained in response to the excitation in the first step. The oscillation is excited by mixing the noise-like signal and the signal received in response to the excitation in the previous step after averaging with a sliding window, the coefficients of which are obtained from the resonance characteristics of the mechanical oscillatory system. A gradual change in the ratio of the amplitude of the noise-like and stationary components of the excitation signal causes a smooth increase in the amplitude of oscillation at a frequency approaching the frequency of the rod's natural oscillations. A numerical and full-scale experiment is carried out to excite mechanical vibrations of a thin metal rod, the end of which is clamped on one side.
Highlights
- Studying the uniformity of electrochemical coating on the outer wall of a thin metal rod by determining the parameters of natural oscillations of this rod.
- The oscillation is excited by mixing the noise-like signal and the signal received in response to the excitation in the previous step after averaging with a sliding window, the coefficients of which are obtained from the resonance characteristics of the mechanical oscillatory system.
- A gradual change in the ratio of the amplitude of the noise-like and stationary components of the excitation signal causes a smooth increase in the amplitude of oscillation at a frequency approaching the frequency of the rod's natural oscillations.
1. Introduction
Coatings applied to the surfaces of components enhance their heat resistance, wear resistance, and corrosion resistance. To apply metallic coatings, methods such as surfacing [1] and electrochemical chroming [2, 3] are commonly used, while for forming oxide coatings, plasma electrolytic oxidation [4, 5] and ion-plasma (magnetron) sputtering of dielectric materials [6] are employed.
The quality of the coating is assessed using various methods, which are chosen based on the purpose and the feasibility of application or accessibility to the surface. Image processing methods are used to assess the condition of coatings [7]. The authors of [8] developed a method for determining the homogeneity coefficient of cast aluminum blanks, which allows predicting the development of damage in surface layers after mechanical processing.
The results of an analytical study on the behavior of coated components with cracks are described in [9]. The paper [10] provides an overview of methods for studying thin coatings on a surface made of ferromagnetic material and classifies methods for studying chromium coatings. The eddy-current method is more accessible and efficient for the study of metal coatings [11].
We consider a mechanical system which is formed by a rod with the metal coating under study. The analytical solution to this problem is quite complex and can be found only with certain simplifications and generalizations [12]. The authors [13] developed a method for determining the first natural frequency of an elastic rod for a three-mass and multi-mass discrete-continuous vibrational system, analytically derived the frequency equation, and compared the results of theoretical studies with those obtained using the finite element method. The influence of the mechanical properties of a metal part on the natural frequencies of the oscillatory system of which this part is a part is considered in [14].
Coatings applied to a surface can change the physical and technical properties of that surface. Ensuring the desired properties depends on the quality of the coating, its thickness and uniformity. These parameters are controlled when accessing the surface. However, the study of the coating in the core of a thin metal rod causes certain difficulties. Therefore, the development of a method for detecting coating inhomogeneity on the outer surface of a thin metal rod is an urgent task.
The aim of the study is to develop a method for excitation and maintenance of mechanical vibrations at the frequencies of natural transverse vibrations of a metal rod to assess the change in the frequency of these modes when the uniformity of the electrochemical coating on the outer wall of this rod changes. The natural vibrations of a mechanical system depend on many parameters related to the geometric position and interconnections of the set of points that make up this system. One of the most informative methods for studying and identifying mechanical objects is to find the parameters of the object's natural oscillations.
The parameters of natural oscillations depend on the way the rod is mounted. When the rod is rigidly mounted at the ends of the rod, the frequencies of the modes with higher amplitudes depend more on the length of the rod and less on the unevenness of the coating. The frequency of the transverse wobble modes is more sensitive to the method of fixing one end of the rod.
The studies have shown that in the presence of a continuous coating and without coating, the frequencies of transverse vibration modes of a rod fixed at one end are practically the same. The presence of an uneven internal coating causes a deviation in the vibration frequencies of transverse modes by fractions of a Hz, specifically in the range of tenths or hundredths of a Hz. The accuracy of the mode frequency determination depends on the time of signal observation. Therefore, it is necessary to excite an oscillation at the frequency of the mode under study and hold this oscillation for a sufficiently long time to determine the oscillation frequency with sufficient accuracy.
2. The model of the system
The oscillations are excited by generating a mechanical force when an alternating current flows in a magnetic field. The system with a rod clamped on one side can be considered an oscillating system with many modes. The force applied to excite the rod is distributed across all modes. To study the oscillating system's behavior, a set of harmonic forces interacting with the rod to produce its velocity must be formed. The force applied causes a velocity increase proportional to the impedance at that frequency.
A proposed approach finds the rod impedance by generating an excitation signal where the total velocity of all modes has a predetermined value. The Ampere force is used to displace the rod. When current flows through part of the rod in a magnetic field, a mechanical force acts on it, causing displacement perpendicular to the magnetic field lines. This rod movement in the magnetic field causes the Lorentz force, inducing an electromotive force. So, the mechanical force is generated by the current, and the rod's speed is determined by the voltage, which relates to the current and speed, setting parameters like maximum current energy used for excitation. The excitation process uses digital processing of sampled data.
The excitation of transverse vibrations of a coated rod is carried out using a broadband signal. At frequencies close to natural frequencies, the energy of the broadband signal remains in the form of vibrations. After obtaining the signal of the rod's vibration amplitude, frequency bands with residual vibrations are identified. Using this result, the spectral density of the broadband signal is adjusted for re-excitation in the next iteration. All components of the spectrum contribute to the oscillations depending on the distance to the frequency under study. The response is associated with an increase in the velocity of the rod at different frequencies. Due to the random appearance of the spectrum under the influence of a noise-like excitation signal, the response spectrum is averaged by the resonance characteristic for further processing.
The differential equation of forced transverse vibrations of an elastic beam with consideration of external viscous friction and longitudinal force is:
where is the deflection function, is the external distributed transverse load, is the longitudinal force, is axial moment of inertia of the beam section, is Young’s modulus, is the density, is the cross-sectional area, external viscous friction force. We put above and obtain Suppose that and the rod is homogeneous. Then the equation has such a form: Its solution can be found by the Fourier method.
Let us formulate the boundary conditions for this equation. In a rigid fixation for 0, the deflection and angle of rotation of the end are zeros:
and at the free end for , the bending moment and transverse force are zero:
However, by using linear combinations of trigonometric and hyperbolic functions, the general solution to the equation of the corresponding Sturm-Liouville problem can be written in terms of such functions: that is
Given the boundary conditions, a nontrivial solution exists if the determinant of the corresponding system of linear homogeneous equations with respect to , , , is zero. In this case, we obtain the following nonlinear equations for finding the frequencies of natural vibrations of the rod and the frequency is determined by the formula oscillations/min, where is the length of rod. The equation’s roots are searched by Shakhno’s method [15]. Here is a brief description of the method. Consider the equation It is known that Newton’s method has a quadratic order of convergence of iterations. Its disadvantage is the need to analytically find the values of derivatives. Therefore, various modifications of Newton’s method are known. In particular, the derivative is often replaced by a difference relation. Shakhno S.M. [15] proposed two-stage modification:
In the case of equation with accuracy we obtain that 1.875104, 4.694091, 10.995540.
Now suppose that, in addition to the reference sample, there are two samples with unevenly applied coatings. The first is rigidly connected to the free end of the reference rod, and the second to the free end of the first. We are interested in answering the following question: is it possible to determine the uniformity of the coating based on the natural vibration frequencies? It can be substantiated that in such a system, the natural vibration frequency of the first and second samples will be determined by the following formulas .
Putting , , ( is the reference mass), we will establish the following asymptotic of the ratio of the frequencies of natural oscillations of the two samples:
The obtained expressions show that it will not be possible to establish the homogeneity of the applied coatings analytically through the ratio of the natural oscillation frequencies.
The principle of operation of the developed device is to pick up the excitation signal, which passes through a metal rod in the form of a current. The selection begins with a random signal. The current at random frequencies interacts with the magnetic field acting on the rod element and moves it. Due to resonance, the energy of the random frequency components remains in the oscillating system. The displacement velocity in the form of voltage is sampled and then each of the spectral components is averaged. To enhance the excitation at frequencies, close to the resonance, another random signal is generated and convolved with the averaged response signal characteristic. The discrete signal for excitation of oscillations is formed by the formula where is the coefficient that depends on the difference between the set and excited energies, is random values with a normal distribution law, is the coefficient of correspondence between the current and the oscillation amplitude, is the result of processing the oscillation rate from the previous step, and . The current is passed through the rod for several periods. After that, the voltage is recorded and discretized into a discrete set of values . Using these discrete values, the spectrum of the response signal is searched .
The response is associated with an increase in the speed of the string at different frequencies. Given the random nature of the spectrum due to the random nature of the excitation signal, the response spectrum is averaged by the resonance response for further processing. All components of the spectrum, depending on their distance from the frequency under study, contribute to the oscillations. The averaged values of the discrete spectral components are sought by the following Eq. (6):
where is the averaging quality factor. By selecting this coefficient, you can optimize the excitation process by changing it from a low value to a high value as the amplitude of oscillations increases. For each of the spectral components, the dispersion in time is searched:
where is the average value of the spectral component for successive excitation cycles, and is the amplitude of the spectral component during the excitation cycles. Based on the found spectrum, the average amplitude value is searched for each of the spectral components. After averaging, the time form is searched for . The process is repeated until one of the following conditions is met: the dispersion of a spectral component has reached a minimum; the maximum number of cycles has passed; the energy of the residual vibration in the rod has reached a specified value.
3. Results
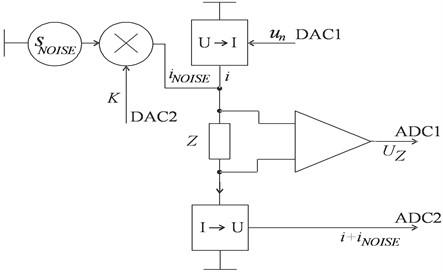
The developed method was used to excite the vibrations of the rod in a magnetic field. The natural frequencies of the rod were investigated in the range up to 1 kHz. The block diagram of the device for selecting the excitation waveform of the rod is shown in Fig. 1. The voltage proportional to the rod movement speed and the excitation current were measured by analogue-to-digital converters ADC1 and ADC2. The excitation signal was supplied to the voltage-current converter from the output of the digital-to-analog converter DAC1. The noise-like signal was generated by a physical noise source, the amplitude of which was controlled by the voltage from the output of DAC2.
Fig. 1Block diagram of the device for excitation of rod vibrations (sNOISE is the source of a noise-like signal, i is the excitation current, iNOISE is the excitation noise current, K is the coefficient of influence, Z the electrical impedance, UZ is the voltage, un is the voltage at the output of the converter, ADC1 is the voltage drop signal, ADC2 is the excitation signal, DAC1 is the signal from a digital-to-analog converter, DAC2 is the signal of the digital-to-analog converter, U→I is the voltage to current converter, I→U is the current to voltage converter)
To investigate the operation of the described method of selecting the excitation signal, a numerical experiment was carried out during which the corresponding parameters were selected.
Fig. 2Results of rod oscillation excitation
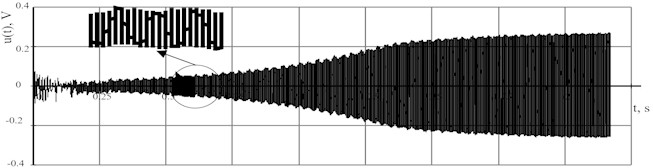
The maximum voltage value was taken: ; the impedance at the selected frequency is accepted: ; force to speed ratio: 0.7; averaging factor 0.993. The results of the increase in the rod oscillation velocity due to the selection of the excitation signal parameters are shown in Fig. 2. The developed method was used to excite the vibrations of the rod in a magnetic field. The natural frequencies of the rod were investigated in the range up to 10 kHz. Therefore, the sampling frequency was chosen to be 22 kHz. The processing was carried out in frames of 2000.
The graph above shows that at the beginning of the excitation, the random signal generated a random rod velocity waveform until modes appeared. After that, the excitation signal was held until the velocity increased to a steady-state value.
4. Conclusions
A method of excitation of natural vibrations of a metal rod by gradual tuning of the filter coefficients, which, using a noise-like signal, forms the spectrum of the excitation signal, has been developed, which made it possible to maintain the rod modes for a long time and increase the accuracy of measuring the frequencies of transverse vibration modes. A sequence of calculations for tuning the excitation signal is proposed and the criteria for the end of the tuning process are introduced. The developed research method is verified by means of numerical experiment and using laboratory tests when a metal rod is excited by a pinch on one side.
References
-
J. Pawlik, J. Cieślik, M. Bembenek, T. Góral, S. Kapayeva, and M. Kapkenova, “On the influence of linear energy/heat input coefficient on hardness and weld bead geometry in chromium-rich stringer GMAW coatings,” Materials, Vol. 15, No. 17, p. 6019, Aug. 2022, https://doi.org/10.3390/ma15176019
-
O. Y. Dubei, T. F. Tutko, L. Y. Ropyak, and M. V. Shovkoplias, “Development of analytical model of threaded connection of tubular parts of chrome-plated metal structures,” Metallofizika i Noveishie Tekhnologii, Vol. 44, No. 2, pp. 251–272, May 2022, https://doi.org/10.15407/mfint.44.02.0251
-
V. S. Protsenko, “Corrosion resistance and protective properties of chromium coatings electrodeposited from an electrolyte based on deep eutectic solvent,” Functional materials, Vol. 25, No. 3, pp. 539–545, Sep. 2018, https://doi.org/10.15407/fm25.03.539
-
M. M. Student et al., “Influence of the composition of electrolyte for hard anodizing of aluminum on the characteristics of oxide layer,” Materials Science, Vol. 57, No. 2, pp. 240–247, Jan. 2022, https://doi.org/10.1007/s11003-021-00538-x
-
L. Ropyak, T. Shihab, A. Velychkovych, O. Dubei, T. Tutko, and V. Bilinskyi, “Design of a two-layer Al-Al2O3 coating with an oxide layer formed by the plasma electrolytic oxidation of al for the corrosion and wear protections of steel,” Progress in Physics of Metals, Vol. 24, No. 2, pp. 319–365, Jun. 2023, https://doi.org/10.15407/ufm.24.02.319
-
Z. A. Duriagina, T. M. Kovbasyuk, and S. A. Bespalov, “The analysis of competitive methods of improvement of operational properties of functional layers of flat heating elements,” Uspehi Fiziki Metallov, Vol. 17, No. 1, pp. 29–51, Mar. 2016, https://doi.org/10.15407/ufm.17.01.029
-
T. Mandziy, I. Ivasenko, O. Berehulyak, and R. Vorobel, “Influence of colour restoration on rust image segmentation,” in IEEE 3rd Ukraine Conference on Electrical and Computer Engineering (UKRCON), pp. 68–73, Aug. 2021, https://doi.org/10.1109/ukrcon53503.2021.9575407
-
Y. Kusyi, O. Kuzin, and N. Kuzin, “The dependence of intergrain damageability of casting on the technological treatment route,” Eastern-European Journal of Enterprise Technologies, Vol. 1, No. 5(79), p. 39, Feb. 2016, https://doi.org/10.15587/1729-4061.2016.59845
-
P. Shats’Kyi, V. Makoviichuk, and B. Shcherbii, “Influence of a flexible coating on the strength of a shallow cylindrical shell with longitudinal crack,” Journal of Mathematical Sciences, Vol. 238, No. 2, pp. 165–173, Mar. 2019, https://doi.org/10.1007/s10958-019-04226-9
-
A. Jones et al., “Continuous in-line chromium coating thickness measurement methodologies: an investigation of current and potential technology,” Sensors, Vol. 21, No. 10, p. 3340, May 2021, https://doi.org/10.3390/s21103340
-
X. Meng, M. Lu, W. Yin, A. Bennecer, and K. J. Kirk, “Evaluation of coating thickness using lift-off insensitivity of eddy current sensor,” Sensors, Vol. 21, No. 2, p. 419, Jan. 2021, https://doi.org/10.3390/s21020419
-
J. Wang, W. T. van Horssen, and J.-M. Wang, “On resonances in transversally vibrating strings induced by an external force and a time-dependent coefficient in a Robin boundary condition,” Journal of Sound and Vibration, Vol. 512, No. 10, p. 116356, Nov. 2021, https://doi.org/10.1016/j.jsv.2021.116356
-
V. Korendiy, V. Gursky, O. Kachur, P. Dmyterko, O. Kotsiumbas, and O. Havrylchenko, “Mathematical model and motion analysis of a wheeled vibro-impact locomotion system,” Vibroengineering Procedia, Vol. 41, pp. 77–83, Apr. 2022, https://doi.org/10.21595/vp.2022.22422
-
Y. Y. Striletskyy and V. A. Rovinskyy, “Method of determination of changes of plastic properties of a metal plate by means of frequencies of modes of the string stretched above it,” Metallofizika i Noveishie Tekhnologii, Vol. 39, No. 10, pp. 1377–1393, Dec. 2017, https://doi.org/10.15407/mfint.39.10.1377
-
I. K. Argyros, S. Shakhno, and H. Yarmola, “On the convergence of Kurchatov-type methods using recurrent functions for solving equations,” Matematychni Studii, Vol. 58, No. 1, pp. 103–112, Oct. 2022, https://doi.org/10.30970/ms.58.1.103-112
About this article
Financial support for research leading to this publication was provided by the NRFU (Project 2023.04/0160). The authors are deeply indebted to Prof. Ivan Shatskyi (Pidstryhach Institute for Applied Problems in Mechanics and Mathematics, NASU) for the justified consultation.
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
The authors declare that they have no conflict of interest.
