Vibrational trimming of book-edge with an eccentrically installed disk knife

1. Introduction

Trimming book edges is a crucial process in the printing industry, significantly affecting the productivity of book production. Various book-trimming machines exist, employing either flat or disk knives to process book edges. However, researchers continue to investigate the cutting process to design more efficient machines that decrease energy consumption and increase productivity. One promising solution is the use of vibrational cutting [6]. By adding vibration to a knife blade, the cutting force can be reduced under certain conditions. Through mathematical modeling of the eccentric blade trajectory during cutting, we discovered that the cutting process could be realized in two different modes: continuous cutting and interrupted cutting [4], [5].

Another experimental research allowed us to establish formulas to approximate the value of a cutting force depending on geometry and kinematic parameters of a disk knife installed without eccentricity [1].

The primary goal of this research is to develop an innovative book block cutting technology that utilizes vibrations in the disk cutting tool using its eccentricity and to determine the optimal parameters for this vibration. This article focuses on the mathematical modeling of the forces generated during cutting with a vibrating disc tool and compares these analytical results with experimental data obtained from a specially designed laboratory setup, replicating conditions close to real-world book production. To achieve this, a new refined mathematical model of the vibrational cutting kinematics was introduced, descripting the cyclic variations in the cutting angle and corresponding forces. The model's predictions regarding the nature and magnitude of force fluctuations during cutting in both vibrational and non-vibrational modes have been validated through experimentally obtained oscillograms.

2. Kinematics of vibrational cutting with an eccentrically installed disk knife

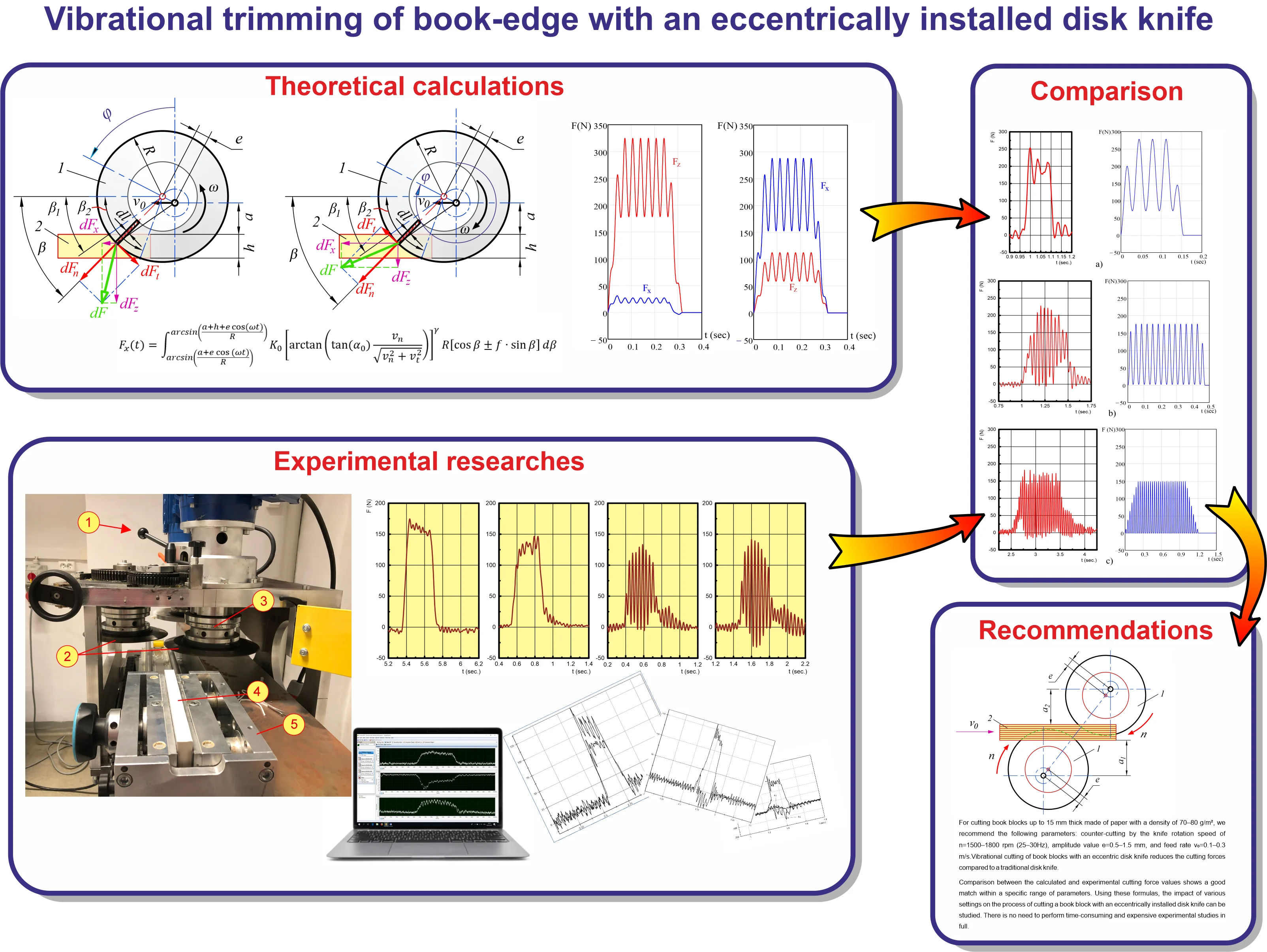
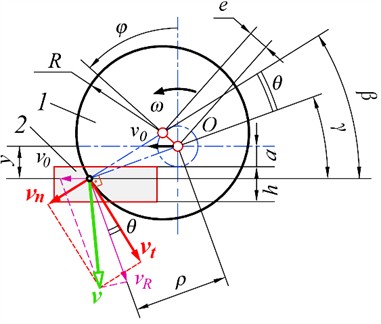
To explore the distribution of velocities of points on the eccentric knife blade during cutting, let’s consider the velocities of points at an arbitrary position, at a distance $y$ from the knife’s axis of rotation. The total velocity at the cutting point consists of two components: the linear velocity $v_R$, and the feed rate $v_0$, (see Fig. 1). The speed rate $v_0$ is known, the linear velocity of a disk blade equals:

For the calculations, we assume that the geometric center of the circular knife is vertically displaced above the center of rotation by the eccentricity value $e$ at the beginning of the knife rotation (when $t=$0). The upper signs in Eq. (1) apply to direct cutting, while the lower signs apply to counter-cutting.

The tangential $v_t$ and normal $v_n$ components equal (see Fig. 1):

where:

A normal component $v_n$, directed along the radius of the knife, represents the plunging velocity of the blade into the book block. A tangential component $v_t$, directed tangentially to the blade and perpendicular to the radius at the blade point, represents the sliding speed of the blade over the book.

Fig. 1Determination of the total speed of an arbitrary cutting point on the knife blade into the block: 1 – disk knife, 2 – book block

a) Direct cutting

b) Counter-cutting

3. The cutting force and its components

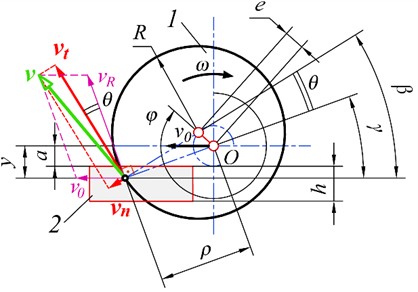
The total cutting force exerted by the blade on the block in the plane of cutting consists of two components:a normal component, directed along the radius, which arises due to the destruction of the sheets of paper as the blade plunges in, and occurs at a speed of $v_n$, and a tangential component, directed tangentially to the blade in the direction perpendicular to the radius of the disk at the blade point. It is the sum of the force of sawing through the layers of paper and the friction force. The sawing occurs at a speed of $v_t$. To visualize this, imagine a disc-shaped knife blade composed of countless infinitesimal straight prismatic blades, each with an infinitely small length $dl$ and a corresponding elemental force, $dF$ (Fig. 2).

Therefore, the elementary cutting force, $dF$, can be treated as the vector sum of its components, $d{F}_n$ and $d{F}_t$. In our experimental research [2], we measured the components of the total cutting force in three directions: the feed direction ($F_x$), the transverse direction ($F_z$), and along the knife’s axis of rotation ($F_y$). The value of the latter component, $F_y$, was found to be negligible compared to the other two, so it was not considered in further analysis.

Fig. 2Determination of components of the elementary cutting force in an arbitrary point on the blade: 1 – disk knife, 2 – book block

a) Direct cutting

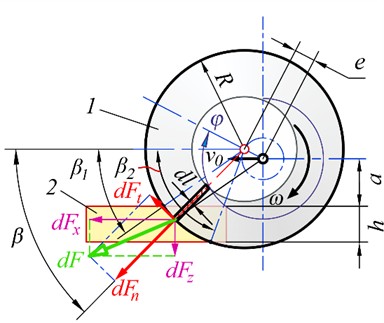
b) Counter-cutting

Due to variations in speed value, direction and position for each elementary knife, the magnitude of the elementary cutting force also varies and depends on the transformed sharpening angle of the blade. The transformed angle for the prismatic knife is given by [7]:

where ${\alpha }_0$– the actual sharpening angle of the blade.

As we consider each individual elementary blade to be a prismatic one, we can use the Eq. (4) for each of them, calculating the speed components with Eqs. (1)-(3). According to the research by various authors the normal cutting force with a flat knife can be accurately approximated by a power dependence [6], [8]. According to our experiments, the ratio between the tangential unit force and the normal unit force remains close to constant [2]. We introduced the sliding cutting coefficient $f$ and expressed the elementary tangential force through it:

where ${\alpha }_T$ – transformed sharpening angle, $K_0$ and $\gamma$ – empiric coefficients. The empiric coefficients depend primarily on the type of paper being cut. We proposed using the same power dependence, as for a flat knife. In our estimation, the coefficients for the offset paper 70,…, 80 g/m² can take the following values: $K_0=$19.3,…, 22.6, $\gamma =$1.6,…, 2.2. The sliding coefficient for the offset paper 70,…, 80 g/m², block thickness of $h=$10,…, 15 mm and the knife’s rotational speed of 1000,…, 2000 rpm can take the value $f=$0.5,…, 0.62.

4. Theoretical calculation of cutting force

In the experimental studies, we measured the magnitudes of longitudinal component of the total cutting force, $F_x$ and its transverse component $F_z$ [2], [3]. To calculate them theoretically, it is necessary to project the vector of the normal force $dN$ onto the $x$ and $z$ directions and integrate the resulting expressions along the cutting arc over the angle $\beta$ within the range from ${\beta }_1$ to ${\beta }_2$ (see Figs. 1 and 2). The magnitude of the cutting force components is determined by Eqs. (6)-(7) considering Eqs. (1)-(5):

The upper signs in Eqs. (6)-(7) apply to counter-cutting, while the lower signs - to direct cutting. Let’s compare these calculations with some experimental data, obtained earlier [2]. The next figure shows some results of the calculations for different cutting parameters according to the Eqs. (6), (7).

Fig. 3Typical theoretical oscillograms of the cutting force components. Disk radius R= 100 mm, disk rotational speed n= 1800 rpm (30 Hz), feed rate v0= 0.5 m/sec, block thickness h= 20 mm, distance of the block from the knife rotation center a= 70 mm, block length L= 130 mm, eccentricity e= 0.5 mm

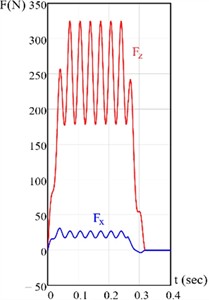
a) Direct cutting

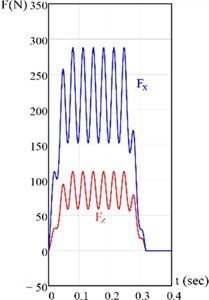
b) Counter-cutting

5. Experimental researches

To validate the theoretical model, a special test stand was designed and built [2], allowing for the study of the vibrational cutting process of book blocks (Fig. 4).

Fig. 4Special stand for investigating book trimming with disc knives. 1 – electrical drive; 2 – disk knives; 3 – eccentricity adjustment mechanism; 4 – book block; 5 – movable carriage with sensors for measuring cutting forces in three directions

The sensors installed on the carriage made it possible to record the three components of the cutting force (longitudinal $F_x$, transverse $F_z$ and vertical $F_y$). The registration system consists of three components: the measuring block, the signal processing block, and the analyzing block. Signal registration and analysis are performed on a PC using specialized software programs LabVIEW SignalExpress and DIAdem from National Instruments. The variable parameters included feed rate (0.25 to 1.5 m/s), knife rotation speed (750 to 2000 rpm, 12.5 to 33.3 Hz), rotation direction (direct cutting or counter-cutting), distance from the book block to the knife’s axis of rotation (0 to 80 mm), eccentricity size (0 to 3 mm), book block thickness (5 to 15 mm), and book block length (100 to 240 mm). The constant parameters were the disk knife diameter (200 mm) and its sharpening angle (26°). Although some tests were performed using different paper types, the majority of experiments utilized 70 g/m² offset paper.

The results of the experimental studies showed that with a rational selection of vibration parameters, it is possible to reduce the cutting force by 1.2 to 1.5 times compared to cutting with a non-vibrating disc knife. Fig. 5 shows typical oscillograms of the longitudinal cutting force $F_x$ when trimming a book block with a disc knife without eccentricity (no vibrations) and with different levels of eccentricity (i.e., blade vibration amplitude).

Fig. 5Recorded oscillograms of the cutting force component Fx by couner-cutting. Disk radius R= 100 mm, its rotational speed n= 1800 rpm (30 Hz), block thickness h= 10 mm, distance of the block from the rotation center a= 82 mm, block length L= 100 mm, feed rate v0= 0.3 m/sec. Vibration amplitude (left to right): e= 0; e= 1 mm; e= 2 mm; e= 3 mm

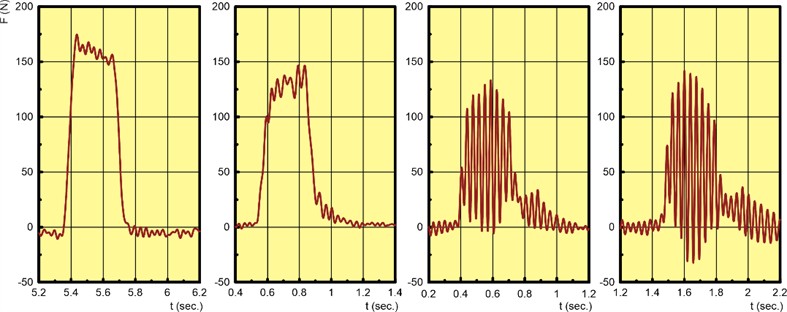
The results of calculations and experiments lead to two main conclusions: cutting forces during counter-cutting will be lower than during direct cutting; the cutting force decreases with an increase in vibration frequency (i.e., with an increase in the knife’s rotation speed). The more detailed analysis of experimental data led to the conclusion that when the eccentricity exceeds 1.5 mm and the knife’s rotation speed is above 1800 rpm (30 Hz), there is a significant increase in noise and vibration throughout the whole equipment, while the reduction in cutting force becomes negligible or disappears altogether due to the emergence of inertial forces.

For cutting book blocks up to 15 mm thick made of paper with a density of 70-80 g/m², we recommend the following parameters: counter-cutting by the knife rotation speed of $n=$1500-1800 rpm (25-30 Hz), amplitude value $e=$0.5-1.5 mm, and feed rate $v_0=$0.1-0.3 m/s.

6. Comparison of the results

Fig. 5 presents a comparison of some experimental (left column) and theoretical (right column) oscillograms of the longitudinal force variation during counter-cutting with a vibrating disc knife. The appropriate theoretical oscillograms (blue ones) was calculated and plotted with PTC MathCAD according to the Eqs. (1)-(7). The recorded oscillograms (red ones) are obtained using the mentioned software LabVIEW SignalExpress, filtered and composed with National Instruments DIAdem.

Fig. 6Recorded (red) and theoretical (blue) oscillograms of the cutting force component Fx by couner-cutting. Disk radius R= 100 mm, its rotational speed n= 1800 rpm (30 Hz), block thickness h= 10 mm, distance of the block from the rotation center a= 70 mm, block length L= 100 mm, eccentricity e= 1 mm

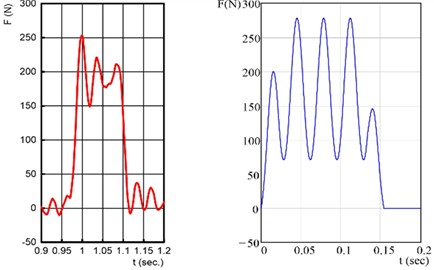
a)$v_0=$0.75 m/sec, continuous cutting

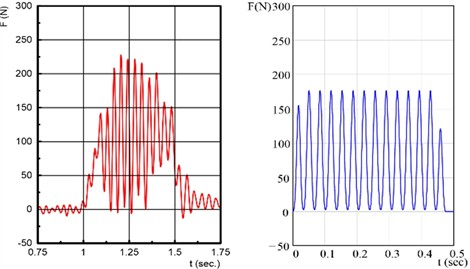
b)$v_0=$0.25 m/sec, continuous

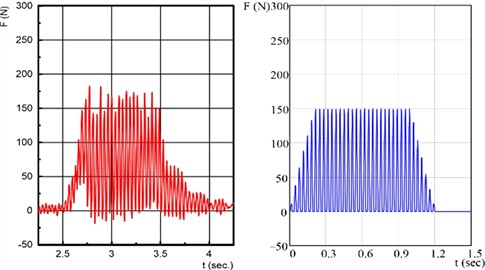
c)$v_0=$0.1 m/sec, interrupted

7. Recommendations

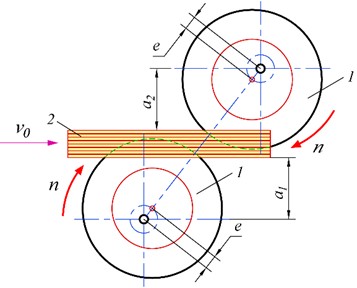
Vibrational cutting using an eccentrically mounted disk can reduce the magnitude of the cutting force, making it reasonable to design such a machine. However, eccentricity introduces vibrations in both the knife and the cutting machine as a whole, it generates noise, and disk knife cannot trim blocks with a thickness over 15 mm due to blade overheating. We propose using two disk knives with identical eccentricity, rotating synchronously in the same direction. This setup could compensate for unbalanced inertial forces and reduce vibrations. In this configuration, one knife performs direct cutting, while the other carries out counter-cutting. Since the cutting force during counter-cutting is lower than during direct cutting, it is more effective to position the block being trimmed asymmetrically so that the cutting depth on the counter-cutter side is greater (Fig. 7). But this prediction needs an experimental verification.

Fig. 7The basic diagram of the design of a proposed cutting machine: 1 – disk knife, 2 – book block, a1<a2

8. Conclusions

Vibrational cutting of book blocks with an eccentric disk knife reduces the cutting forces compared to a traditional disk knife. The presented formulas allow theoretical prediction of cutting force and its components. The experimental results made it possible to develop recommendations for selecting the optimal parameters for vibrational cutting (see section 5).

Comparison between the calculated and experimental cutting force values shows a good match within a specific range of parameters. Using these formulas, the impact of various settings on the process of cutting a book block with an eccentrically installed disk knife can be studied. There is no need to perform time-consuming and expensive experimental studies in full.

But the presented method for calculating cutting forces does not take into account the elasticity and deformation of the book block and uses simplified empirical formula. As a result, its applicability is limited to a narrow range of parameters. Cutting with only one eccentric knife was studied experimentally, whereas cutting with two knives is expected to yield better results. Therefore, further experimental and theoretical research in this area is essential.