Application of complex function solution methods to determine the exciting load required for vibratory compaction of metal powder

1. Introduction

The vibratory compaction of metal powder is a key process in producing metal powder products, relying on the interaction between a vibrating body and a powder mixture, often with an anisotropic structure. Compaction efficiency is influenced by parameters like the amplitude and frequency of oscillations and the duration of vibration. In industry, oscillation amplitudes reach up to 0.4 mm, with frequencies ranging from 10,000 to 20,000 cycles per minute. These parameters must be adjusted based on the metal powders’ physical and mechanical properties to maximize product benefits. Different powder structures mean that standard vibration modes, without material-specific considerations, can limit effectiveness, highlighting the need for theoretical analysis.

The interaction between a vibrating body and the media has been modeled using rheological frameworks, integrating elastic, plastic, and frictional components: Hooke’s elastic model [1], Newton’s viscous model [2], the Kelvin-Voigt viscoelastic model [3], the Bingham model [4], and the Zener model [5], which accounts for reversible and irreversible deformations. Kuhn [5] further described stress relaxation using the Maxwell model [6], which combines elastic and viscous elements, as well as more complex multi-element models.

The method of complex functions, first applied in [7] to determine the amplitude of excitation for asphalt concrete compaction, was later extended to calculate the load for polymer concrete [5]. These models used specific rheological frameworks, and the method provided practical solutions aligned with experiments.

The generalized Kelvin medium rheological model accurately represents the vibratory compaction of metal powders, particularly in analyzing the damping of excitation amplitude due to internal friction. However, existing studies have not used this model for powder behavior or applied the wave equation to characterize vibrations during compaction. Therefore, it is essential to conduct theoretical studies using complex functions to determine the required excitation load for effective metal powder compaction. This research aims to apply the generalized Kelvin medium model combined with complex function methods, offering a novel approach to metal powder compaction.

2. Research methodology

2.1. Theoretical model

In this study, we employ the solution method in complex functions to theoretically determine the amplitude of oscillations and the corresponding vibration load required for the compaction of metal powder [8]. The elastic-viscous properties of the powder medium are represented using a rheological model (Fig. 1) where the equation is inside the table with no borders.

Fig. 1Rheological model of the compacted powder medium under load

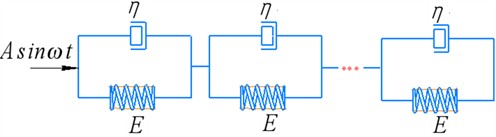
The following equation describes the relationship between stress and strain for this rheological model:

1

$\sigma \left(x,t\right)=E\bullet \frac{\partial u\left(x,t\right)}{\partial x}+\eta \bullet \frac{\partial u(x,t)}{\partial t},$

where $u$ and $x$ – Eulerian and Lagrangian coordinates, respectively; $\sigma$ – stress that develops in the compacted volume of metal powder; $E$ – dynamic modulus of elastic deformation of the metal powder; $\eta$ – dynamic viscosity coefficient, accounting for internal friction within the metal powder.

Consider the deformation process of a metal powder layer (Fig. 1). Assuming that the density $\rho$ within each elementary volume of the metal powder remains constant, with abrupt changes occurring only at the transitions between adjacent volumes, we focus on the movement of the compacted medium in the direction of the elementary volume and over time. Consequently, in this one-dimensional case, the differential equation of motion for the powder medium can be expressed as follows:

2

$\frac{\partial \sigma }{\partial x}=\rho \bullet \frac{{\partial }^{2}u}{\partial t^2},$

or, considering Eq. (1):

3

$E\bullet \frac{{\partial }^{2}u\left(x,t\right)}{\partial x^2}+\eta \bullet \frac{{\partial }^{2}u\left(x,t\right)}{\partial x\partial t}=\rho \bullet \frac{{\partial }^{2}u}{\partial t^2}.$

The wave Eq. (3) was solved using the following established boundary conditions [7]:

4

$u\left(0,t\right)=A\bullet \sin \left(\omega \bullet t\right),\mathrm{}\mathrm{}\mathrm{}\mathrm{}u\left(H,t\right)=0,$

where $H$ – the height of the compacted metal powder layer.

The solution of Eq. (3) is presented as the imaginary part of a complex number [7]:

5

$u\left(x,t\right)=Im\bullet \left[u\left(x\right)\bullet e^{i\omega \bullet t}\right].$

For convenience, the sign of the coefficient will be omitted in subsequent steps. Substituting Eq. (5) into Eq. (3) yields the equation for determining the complex amplitude of oscillations:

6

$\frac{{\partial }^{2}u\left(x,t\right)}{\partial x^2}+\frac{i\eta \omega }{E}\bullet \frac{\partial u\left(x\right)}{\partial x}+\frac{\rho \bullet {\omega }^2}{E}\bullet u\left(x\right)=0.$

The solution of Eq. (6) will have the form:

7

$u\left(x\right)=e^{-\frac{i\eta \omega }{2E}x}\bullet \left(D_1\bullet \cos \left(k\bullet x\right)+D_2\bullet \mathrm{s}\mathrm{i}\mathrm{n}(k\bullet x\right)),$

where $D_1$ and $D_2$ – integration constants (complex amplitudes) are determined by the boundary conditions Eq. (4); and $k$ – wave number:

8

$k=\frac{\omega }{2E}\bullet \sqrt{4\bullet E\bullet \rho +{\eta }^2}.$

The wavenumber can be expressed as:

9

$k=\frac{\omega }{c},$

where $c$ – phase speed of excitation propagation.

The following relationships were derived after a series of transformations:

10

$u\left(x,t\right)={A\bullet e}^{-\frac{i\eta \omega }{2E}x}\bullet \left[\frac{\sin \left(k\bullet \left(H-x\right)\right)}{\sin \left(k\bullet H\right)}\right]\bullet e^{i\omega t}.$

Define $e^{-\frac{i\eta \omega }{2E}x}$ in Eq. (10) as follows:

11

$e^{-\frac{i\eta \omega }{2E}x}=\mathrm{c}\mathrm{o}\mathrm{s}\left(\frac{\eta \omega x}{2E}\right)-i\bullet \mathrm{s}\mathrm{i}\mathrm{n}\left(\frac{\eta \omega x}{2E}\right).$

Using Eq. (11) as a basis, solution Eq. (10) can be transformed into the following form:

12

$u\left(x,t\right)=A\bullet \left[\frac{\mathrm{c}\mathrm{o}\mathrm{s}\left(\frac{\eta \omega x}{2E}\right)\bullet \sin \left(k\left(H-x\right)\right)-i\bullet \mathrm{s}\mathrm{i}\mathrm{n}\left(\frac{\eta \omega x}{2E}\right)\bullet \mathrm{s}\mathrm{i}\mathrm{n}\left(k\left(h-x\right)\right)}{\mathrm{s}\mathrm{i}\mathrm{n}(k\bullet H)}\right]\bullet e^{i\omega t},$

where $u$ and $x$ – Eulerian and Lagrangian coordinates, respectively; $\sigma$ – stress that develops in the compacted volume of metal powder; $E$ – dynamic modulus of elastic deformation of the metal powder; $\eta$ – dynamic viscosity coefficient, accounting for internal friction within the metal powder.

Similarly to Eq. (11), and considering that $e^{i\omega t}=\mathrm{c}\mathrm{o}\mathrm{s}\left(\omega t\right)+i\bullet \mathrm{s}\mathrm{i}\mathrm{n}\left(\omega t\right)$, the solution to Eq. (3) that satisfies boundary conditions Eq. (4) is found in the following form:

13

$u\left(x,t\right)=\frac{A}{\mathrm{s}\mathrm{i}\mathrm{n}(k\bullet H)}\bullet \left(\mathrm{c}\mathrm{o}\mathrm{s}\left(\frac{\eta \omega x}{2E}\right)\bullet \sin \left(k\left(H-x\right)\right)\bullet \sin \left(\omega t\right)-\mathrm{s}\mathrm{i}\mathrm{n}\left(\frac{\eta \omega x}{2E}\right)\right.$
$\bullet \mathrm{s}\mathrm{i}\mathrm{n}\left(k\left(H-x\right)\bullet \cos \left(\omega t\right)\right).$

Thus, Eq. (13) is the final solution of the wave Eq. (3), satisfying the boundary conditions Eq. (4). This solution describes the propagation of waves in the compacted layer of metal powder and serves as the basis for further analysis of the vibration compaction process.

3. Results and discuss

The application of the complex functions method to solve the wave equation for the vibratory compaction of metal powder yielded significant insights into the process dynamics. The key theoretical finding is expressed in Eq. (14), which describes the stress developed in the compacted layer as a function of various parameters:

This equation demonstrates that the stresses generated during compaction are influenced by several factors: dynamic modulus of elastic deformation ($E$), coefficient of dynamic viscosity ($\eta$), powder density ($\rho$), layer thickness ($h$), wave number ($k$), amplitude ($A$) and angular frequency ($\omega$) of excitation.

The stress amplitude is directly proportional to the excitation amplitude, highlighting the importance of selecting appropriate vibration parameters to achieve the desired powder density throughout the entire thickness of the compacted layer.

By substituting specific values for the x and h coordinates into Eq. (14), we can determine how stresses change at different points in the metal powder layer:

Surface stress ($x=$ 0):

Base stress ($x=h$):

These equations provide valuable insights into the stress distribution within the compacted layer, which is crucial for optimizing the compaction process.

To achieve effective compaction, the stress generated must exceed a critical value ${\sigma }_{0i}$, which represents the minimum stress required to break down the structure of the powder mixture. This condition is expressed as:

Based on this condition, we can derive an expression for the required excitation amplitude:

This formula allows for the calculation of the necessary surface excitation amplitude to achieve complete compaction of the metal powder, taking into account its specific properties and the desired compaction parameters.

The theoretical analysis presented here builds upon the analytical method proposed by Prof. A. Maslov, extending it to the specific case of metal powder compaction using the Kelvin rheological model. This approach provides a robust framework for optimizing vibratory compaction processes in industrial applications.

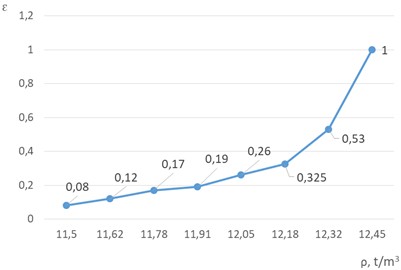
Experiments conducted using the laboratory vibration table provided valuable data on the kinetics of the compaction process. Based on the experimental and calculated data of the amplitude of oscillations A, a change in the density of the powder mixture was found depending on the dynamic pressing pressure. Based on the obtained results, a graph was constructed that reflects the kinetics of the compaction process of the powder mixture depending on the relative deformation $\epsilon$ (Fig. 2). The graph visually represents how the density of the tungsten powder mixture changes with increasing relative deformation. The curve shows a non-linear relationship, with density increasing more rapidly at lower deformation values and then gradually leveling off at higher deformations.

By analyzing the graph, we can identify different stages of the compaction process:

Initial stage (0 $<\epsilon <$ 0.1): Rapid increase in density, likely due to particle rearrangement and filling of large voids.

Intermediate stage (0.1 $<\epsilon <$ 0.3): Continued increase in density but at a decreasing rate, possibly due to plastic deformation of particles.

The final stage ($\epsilon >$ 0.3): The curve begins to plateau, indicating that further deformation results in diminishing returns in terms of density increase.

The graph suggests that the most efficient compaction occurs in the relative deformation range of 0.1 to 0.3, where the slope of the curve is steepest. The shape of the curve provides information about the material’s response to dynamic pressure. The tungsten powder mixture shows good compressibility initially but becomes increasingly resistant to further densification at higher deformation levels.

This information allows for better control of the compaction process by providing a clear relationship between applied pressure (which relates to deformation) and resulting density.

Fig. 2The kinetics of the tungsten powder mixture compaction process as a function of relative deformation

4. Conclusions

The theoretical studies conducted have yielded several key parameters, including the phase speed of excitation propagation and the absorption coefficient, which characterizes the decrease in excitation as it moves away from the source. Additionally, analytical expressions have been derived to calculate the amplitude of stress occurring on the surface and at the base of the compacted metal powder layer, depending on the coordinate. An analytical expression has also been developed to determine the excitation amplitude necessary for complete compaction of the metal powder surface based on specific compaction conditions. The findings significantly advance the understanding of metal powder compaction and provide valuable tools for improving the efficiency and quality of powder metallurgy processes. Future research could focus on extending this model to a wider range of powder materials and exploring the effects of particle size distribution on compaction behavior.