Processing piano audio: research on an automatic transcription model for sound signals

1. Introduction

The inheritance and development of music are very important [1]. With the application of digitalization, informatization, and other methods in the field of music, there has been increasing research on the recording and preservation of music. Automatic transcription of sound signals involves converting raw audio into music notation or musical instrument digital interface (MIDI) data, which plays an important role in various applications [2]. It supports music information retrieval (MIR) [3], enables error checking of audio via scores, and improves the efficiency of score annotation, reducing human resources and the cost of implementation. In music composition, real-time recording of music scores can be achieved through automatic transcription models, facilitating composers' modifications. Automatic sound signal transcription is based on the perspective of signal processing, and many relevant methods have been applied [4]. Simonetta et al. [5] proposed a hidden Markov model-based method for note-level pairing and verified its reliability through experiments on multiple datasets. Meng and Chen [6] employed the Mel-frequency cepstral coefficient (MFCC) for timbre judgment and constant Q transform (CQT) for pitch judgment. They utilized a convolutional neural network (CNN) to achieve automatic transcription and obtained a recognition success rate of 95 %. Alfaro-Contreras et al. [7] studied the effect of combining different modalities (e.g., image, audio) in automatic transcription and found that two modalities could effectively improve the single-mode recognition framework. Lee [8] designed a method using Stein’s unbiased risk estimator and eigenvalue decomposition for automatic transcription and found a 2 %-3 % improvement in F1 value compared to traditional approaches. Marolt [9] proposed an automatic transcription method for polyphonic piano music based on an auditory model and adaptive oscillator network. They discovered that the oscillator network can improve the accuracy of neural network transcription. Ryynanen and Klapuri [10] extracted three acoustic features through a multi-fundamental frequency estimator, implemented music transcription by searching multiple paths in the note model, and achieved 41 % precision and 39 % recall rate. Benetos and Dixon [11] simulated the temporal evolution of music tones and proposed a polyphonic music transcription method based on a hidden Markov model. The method achieved better results than the non-temporal-constrained model in multi-instrument recordings. Ju et al. [12] proposed a method for recognizing the duration of musical notes considering time-varying tempo. They conducted experiments on transcribing 16 monophonic children’s songs and achieved matching rates of 89.4 % and 84.8 % for note duration and pitch recognition, respectively. O'Hanlon et al. [13] presented a greedy sparse pursuit approach based on nearest subspace classification, applied it in automatic music transcription, and verified its effectiveness. Cazau et al. [14] developed a Markov model-based general transcription system that can host various prior knowledge parameters. They also created a sound corpus for experiments and performed comparative evaluations on the transcription results. Wang et al. [15] calculated the timbre vector based on the short-time Fourier transform and peak detection algorithm and classified timbres using a support vector machine to achieve automatic transcription. The method achieved a hit rate of 73 % on a small database containing two timbres. The piano is a keyboard instrument [16]. Given the wide range of registers and common usage in solo and accompaniment, the study of automatic transcription modeling for piano audio holds paramount importance. However, the performance of many transcription systems is still significantly lower than that of human experts [17], and some automatic transcription models for piano audio have poor transcription effects, which cannot yet meet the needs of practical applications. In order to obtain a more efficient automatic transcription mode, this paper processed piano audio using the CQT and extracted features. Subsequently, an automatic transcription model based on CNN and Transformer was designed. The effectiveness of the proposed approach was verified through experiments on a dataset. The approach offers a novel and reliable technique for practical piano audio processing and provides theoretical support for the further study of CNN and Transformer architectures in automatic sound signal transcription, which is beneficial to the further development of automatic transcription models. Moreover, this article also provides a theoretical reference for the transcription of other music, which is advantageous to the more profound development of the field of music information retrieval.

2. Piano audio and constant-Q transform

The piano produces sound by striking the keys and driving the strings to vibrate. Its sound signal is a superposition of a series of sinusoidal signals. The core sounding part can be called the fundamental, which determines the pitch. The corresponding frequency is the fundamental frequency. By identifying the fundamental frequency of piano audio, it is possible to identify the pitch. Scientific pitch notation is generally used in music based on the letters C, D, E, F, G, A, and B. In the digital domain, MIDI [18] is used to indicate. The relationship between the MIDI and fundamental frequency $f$ is written as Eq. (1):

In 88-key pianos, the pitch range is A0-C8, and the MIDI numbering range is 21-108, corresponding to a fundamental frequency range of 27.5-4186 Hz.

Before transcription, extracting features from the original piano audio data is necessary to achieve the signal transformation from the time domain to the frequency domain and provide reliable feature input for the automatic transcription model. The short-time Fourier transform (STFT) has an extensive range of applications in sound signal processing [19] and has good performance in various speech recognition tasks [20]. The computational formula can be written as Eq. (2):

where $w\left[n\right]$ is the window function, $x\left[n\right]$ is the original sound signal, and $N$ is the window length, which directly affects the time and frequency resolution of the spectrogram. The main drawback of STFT is that it obtains the same frequency resolution at high and low frequencies, which is not conducive to recognizing piano tones. Therefore, this paper chooses another frequency domain feature, CQT [21], as the piano audio feature.

CQT is characterized by its window length changing with frequency, thus ensuring high resolution at low frequencies. In CQT, there exists a quality factor $Q$, as shown in Eq. (3):

where ${\delta }_{f_k}$ is the bandwidth of the $k$-th filter. Combined with $Q$, the window length is written as $N=N\left[k\right]=Q\bullet \left(f_s/f_k\right)$, where $f_s$ is the sampling frequency. The final CQT formula can be written as Eq. (4):

In automatic transcription, mono sampling data are mainly used for analysis. To obtain comprehensive characteristics, this paper uses a dual-channel approach to read the data and obtains a dual-channel CQT spectrogram as input to the transcription model.

3. Automatic transcription model for sound signals

3.2. CNN-Transformer transcription model

One of the main advantages of a CNN is its ability to capture local features in a sequence. However, it has limitations when it comes to processing long sequences. To address this issue, CNN is often integrated with a recurrent neural network (RNN) to handle time series features. However, this combined architecture tends to have low training speeds. The Transformer model, which utilizes an encoder-decoder structure, offers high training speeds and has shown excellent performance in various tasks such as machine translation and speech recognition [23]. The present study proposes combining the Transformer model with a CNN to construct an automatic transcription model.

The Transformer model relies on a multi-head self-attention mechanism [24] to effectively capture sequence information. Firstly, a linear transformation is performed on input sequence $x$ to get three sequences, $Q$ (Query), $K$ (Key), and $V$ (Value), and then the attention is obtained, as shown in Eq. (7):

7

$Attention\left(Q,K,V\right)=softmax\left(\frac{{QK}^T}{\sqrt{d_k}}\right)V,$

where $Q$, $K$, and $V$ are the Query, key, and Value indicators, $d_k$ refers to the dimension of Key. The multi-head attention splices the output of each attention and passes it into the linear layer for linear transformation. The formula of the multi-head attention is shown in Eq. (8):

8

$MultiHeadAttention=concat\left({head}_1,{head}_2,\cdots ,{head}_h\right)W^O,$

9

${head}_i=Attention\left(Q{W}_i^Q,K{W}_i^K,V{W}_i^V\right),$

where $W$ is the weight matrix and $h$ is the number of heads in the attention.

A residual and normalization layer follows the multi-head self-attention layer to avoid network degradation. Then, a two-layer FC layer is employed to obtain the new representation vector, as shown in Eq. (10):

10

$FCN\left(x\right)=max\left(0,x{W}_1+b_1\right)W_2+b_2,$

where $x$ is the input vector, $W$ and $b$ are the weight and bias of every layer.

In the Transformer model, residual connections are used between the input and output of each layer to alleviate the problem of gradient vanishing. Layer normalization is then applied after the residual connection to accelerate training and improve robustness, making the model more stable.

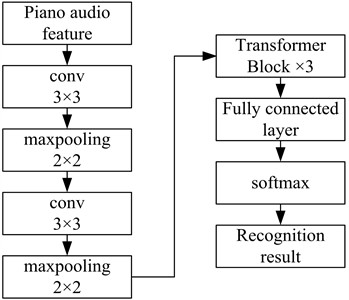
The CNN can effectively capture local features in a sequence, and the Transformer model can effectively treat the logical dependency relationship. Therefore, combining a CNN with a Transformer can better capture both local and global information in sound signals, thereby improving the effectiveness of automatic transcription for piano audio. The structure of the designed CNN-Transformer transcription model is illustrated in Fig. 1.

The transcription model comprises two CNN layers and three Transformer layers. The dual-channel CQT spectrogram extracted in the last section is used as the model input. There are two CNN layers on the left. Each CNN layer has a 3×3 convolutional layer followed by a 2×2 maximum pooling layer. The input size of the first CNN is 128×2, the size of the convolution kernel is 3×3, and the size of the output channel is 32. The input size of the pooling layer is 128×2, the size of the pooling kernel is 2×2, the step size is 2, and the output size is 64×1. The input size of the second CNN is 64×32, the size of the convolution kernel is 3×3, and the number of output channels is 64. The input size of the second pooling layer is 64×32, the size of the pooling size is 2×2, the step size is 2, and the output size is 32×1. After the processing by the two CNN layers, the feature vector obtained is 32×64. The resulting feature vectors are fed into the Transformer layer on the right for further processing. Each Transformer layer comprises four multi-head attention layers and two FC layers. After feature extraction by three layers of Transformer, the outputs are concatenated in the FC layers. Finally, the features are input into the softmax layer to recognize the piano audio.

Fig. 1The CNN-Transformer transcription model

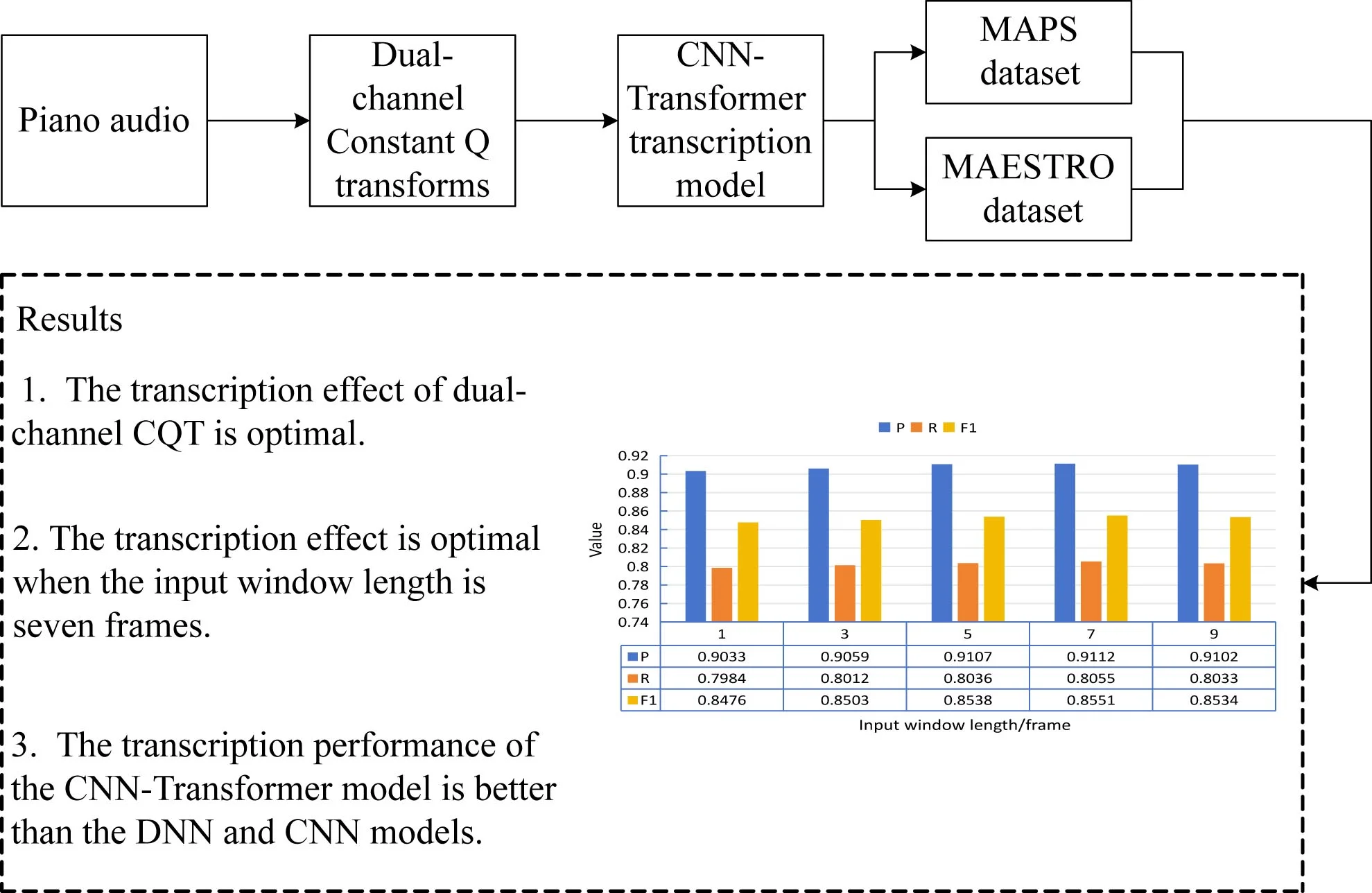
4. Results and analysis

5. Analysis of results

Using the MAPS dataset, the transcription effects of STFT, mono CQT, and dual-channel CQT were compared, and the outcomes are presented in Table 1.

It was seen that the transcription result using STFT was poor, with an F1 value of 0.7894 at the frame level, an F1 value of 0.7780 at the note level (no cutoff), and an F1 value of 0.5396 at the complete note level. These results indicated that STFT failed to effectively differentiate piano notes when used as an input to the transcription model. In contrast, the comparison between mono CQT and dual-channel CQT revealed that the dual-channel CQT achieved better results. At the frame level, the dual-channel CQT achieved an F1 value of 0.8551, showing a 0.02 improvement compared to mono. At the note level (no cutoff), the F1 value was 0.8521, showing a 0.0323 improvement compared to mono. Additionally, the F1 value was 0.6191 at the complete note level, demonstrating a 0.0308 improvement compared to mono. These findings concluded that employing the dual-channel CQT technique led to better outcomes in the automatic transcription of piano audio. In comparing frame level, note (no cutoff), and complete note transcription, it can be seen that the difficulty of transcribing complete notes was the highest, resulting in the worst transcription results. However, the dual-channel CQT used in this article still demonstrated the best performance, with an F1 value of 0.6191, further proving the advantage of using dual-channel CQT as a feature.

Considering the sensitivity of the model to the input window length, various input window lengths were chosen to analyze the impact of the sliding window on transcription results. The frame-level recognition results are presented in Fig. 2.

Fig. 2The sensitivity analysis results of the input window length

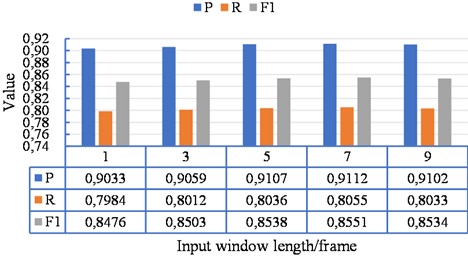
It was found that the optimal transcription results (a P value of 0.9112, a R value of 0.8055, an F1 value of 0.8551) were achieved with an input window length of seven frames. When the number of frames was small, the spectrum contained less information, resulting in poor recognition of piano notes. As the number of frames increased, the amount of information provided in the spectrum gradually increased, leading to a gradual improvement in the model’s P value, R value, and F1 value. However, when the growth reached nine frames, the results were inferior to those obtained with seven frames. For example, the F1 value decreased to 0.8524, which was 0.0017 smaller than that when it was seven frames. It is because the large sliding window caused the merging of similar notes, which negatively impacted the recognition results. Therefore, when this model is used for transcription, better results can be obtained when the input window length is 7.

A sensitivity analysis was performed on the CNN layer number in the model. The transcription results of the frame level under different convolutional layers are presented in Table 2.

It can be seen that when only one CNN layer was used, the CNN-Transformer model obtained a P value of 0.8554, a R value of 0.7492, and an F1 value of 0.7988 for the MAPS dataset. When two CNN layers were used, this model exhibited the best transcription performance, with an F1 value of 0.8551. When the number of layers continued to increase, the transcription effect declined. These results demonstrated the correctness of using two CNN layers.

Next, the CNN-Transformer model was compared to the deep neural network (DNN) [29] and CNN models, and the frame-level results for MAPS and MAESTRO datasets are presented in Table 3.

It was found that the DNN model yielded inferior transcription results for both the MAPS and MAESTRO datasets, with an F1 value of only 0.6970 for MAPS and 0.6991 for MAESTRO. The CNN model showed relatively better results. It obtained an F1 value of 0.8152 for the MAPS dataset and an F1 value of 0.8670 for the MAESTRO dataset, which was increased by 0.1182 and 0.1679 respectively compared to the DNN model. These results demonstrated its more robust feature extraction capability for piano audio processing. Furthermore, the CNN-Transformer model achieved an F1 value of 0.8551 for MAPS, showing a significant improvement of 0.0399 compared to the CNN model. Similarly, for the MAESTRO dataset, the CNN-Transformer model achieved an F1 value of 0.9042, demonstrating an improvement of 0.0372 compared to the CNN model. These results validated the advantage of combining the Transformer with the CNN architecture for piano audio transcription.

6. Conclusions

This paper designed a CNN-Transformer automatic transcription model for recognizing piano notes by processing piano audio and extracting the dual-channel CQT spectrum. Experiments conducted on the MAPS and MAESTRO datasets obtained the following results.

1) The STFT and mono-channel CQT performed poorly; the dual-channel CQT obtained the optimal results in the transcription of frame levels, notes (no cutoff), and complete notes, with F1 values of 0.8551, 0.8521, and 0.6191, respectively.

2) The input window length could affect transcription results. When the input window length was 7, the transcription result was the best: the P, R, and F1 values for the frame-level transcription were 0.9112, 0.8055, and 0.8551, respectively.

3) The CNN layer number in the CNN-Transformer model could affect transcription results. When there were two CNN layers, the transcription performance was the best.

4) The CNN-Transformer model performed superior results in frame-level transcription compared to the CNN and CNN models.

The results demonstrated the advantages of the CNN-Transformer model, which was designed using the dual-channel CQT, in transcribing piano audio and its application usability in practical transcription. However, this study also has some limitations. For example, there is a lack of a more comprehensive piano audio database, and only one type of feature with superior performance was selected for feature selection without considering the comparison of more features. In future work, further exploration will be conducted on feature selection in piano audio transcription, collecting actual piano audio data will be considered to establish a database, and the CNN-Transformer model will be further optimized to achieve better transcription performance.