Abstract
The gymnasium is mainly composed of truss structure, with a large span, and requires high seismic performance. To ensure greater stability of the truss structure, modal analysis was conducted on the mechanical model, yielding the natural frequencies and modal shapes. In order to improve the seismic performance, BRB rods were added to the support points, and the frame structure was reinforced with diagonal braces. Through modal verification, it can be seen that the stiffness of the truss structure was significantly improved. The internal forces of the truss were simulated under the El Centro and Taft seismic wave conditions. The results show that the optimized structure can significantly reduce the internal forces and improve the overall seismic performance. The fundamental natural period of the reinforced structure is less than that of the unreinforced structure, and the stiffness of the reinforced steel structure increases, making it more sensitive to vertical seismic motion.
Highlights
- To ensure greater stability of the truss structure, modal analysis was conducted on the mechanical model, yielding the natural frequencies and modal shapes.
- In order to improve the seismic performance, BRB rods were added to the support points, and the frame structure was reinforced with diagonal braces.
- Through modal verification, it can be seen that the stiffness of the truss structure was significantly improved.
1. Introduction
With the continual refinement of theoretical models and the progressive advancement of construction technology, large-span truss structures are increasingly prevalent in architectural projects such as gymnasium. In designing the structure of gymnasium, apart from satisfying the load-bearing requirements stipulated by regulations, it is also essential to fulfill specific performance criteria under exceptional circumstances, such as seismic resistance [1-2]. The gymnasium contains numerous truss structural members with varying dimensions and shapes, resulting in different forces and corresponding actions. Furthermore, the dynamic response of the entire structure varies significantly under different excitation vibrations [3]. Therefore, it is imperative to analyze the modal characteristics to effectively predict the specific damage state and potential collapse behavior of the structure [4-5]. A truss structure with a large span exhibits superior overall integrity compared to other structures. By analyzing the modal characteristics of the truss structure, it is possible to assess the overall damage state and select an appropriate reinforcement method to enhance its resistance against collapse under various excitation vibrations.
The stiffness of the structure is very critical to its seismic performance, and it can provide some basis for seismic performance research and corresponding reinforcement research [6]. Modal analysis is a crucial method for assessing the seismic resistance capacity of truss structures. Through modal analysis, dynamic characteristic parameters such as frequency, mode shape, and damping ratio can be obtained, which are directly linked to the seismic performance of the structure. Modal analysis enables the acquisition of acceleration response data from environmental excitation sources through simulation or measurement means, and these dynamic characteristic parameters serve as the foundation for evaluating the seismic performance of structures. The large-span tube truss structure needs to consider the effects of both horizontal and vertical earthquakes and should not be controlled in a single direction only. Therefore, in the field of structural control, by utilizing the development of computer technology and simulation software, finite element simulation of steel structures can be carried out, and the corresponding data can be analyzed, which can provide effective protection measures, which are of great significance for protecting lives and property safety.
2. Modal characteristics analysis
2.1. Finite element modeling
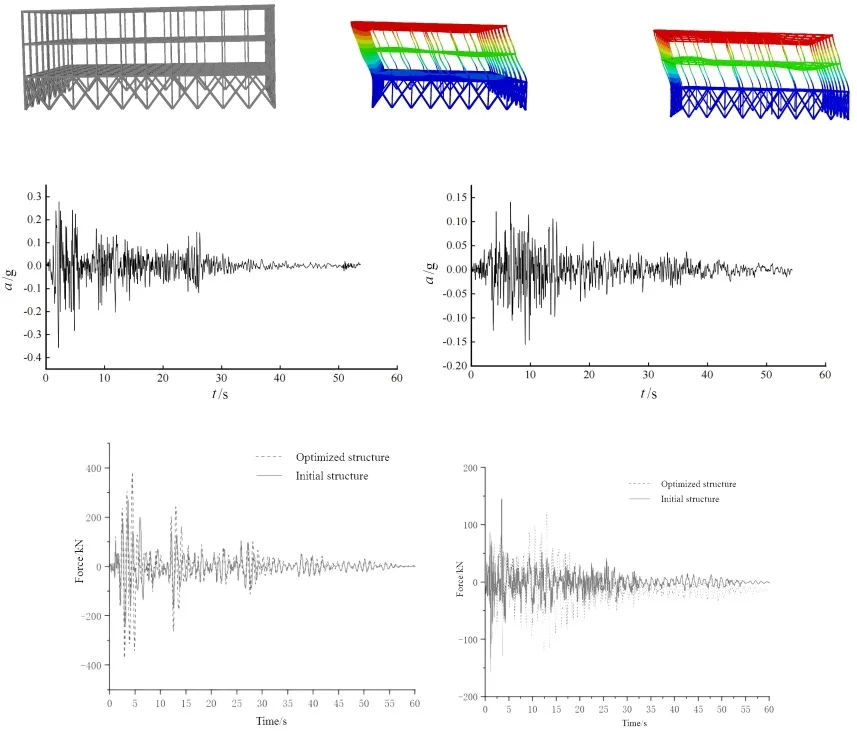
Based on Abaqus, a finite element model was established for the steel structure indoor gymnasium with a span of 60 m, width of 40 m, and a height of 18 m, as shown in Fig. 1. The model consists mainly of steel columns and beams. The roof is designed as a steel frame structure. The building has a total of 3 floors, with a floor height of 6 m. The steel columns are selected as box sections, and the same section size is used for all columns. The beams on each floor are selected as H-shaped sections, and the section size is the same for all beams. To prevent the steel floor from excessive deflection, two steel columns were added in the center of each floor as support points to reinforce the floor and ensure that the steel structure deflection meets the code requirements. Since the first floor is most affected by earthquakes, a diagonal brace was added to the steel structure model of the first floor to increase its stiffness.
Fig. 1The main structural of gymnasium truss
a) The structure of trusses
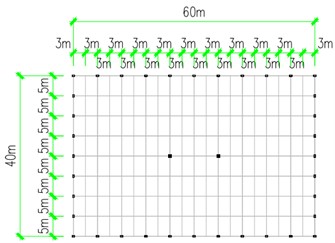
b) The ground floor plan
2.2. Computation of modal properties
The modal characteristics of structures are a self-related dynamic characteristic. By analyzing them, the structure itself can be avoided from resonance under seismic excitation conditions, thus avoiding serious damage. Among the many methods for studying the seismic performance of structures, modal analysis can greatly reduce the calculation time, making it the most used and effective method in linear analysis. Modal analysis is the most effective approach for determining the vibration characteristics of structures. By integrating modal shape analysis into the model, the structural load performance and identify potential weaknesses can be enhanced. The Lanczos algorithm was used to perform modal analysis of the steel structure. The calculated results of the first 20 modal frequencies are shown in Table 1. It can be seen that the first eigenmode period of the structure is short, at 1.2242 s, with a frequency of 0.8168 Hz. As the modal order increases, there is no obvious jump in the period and frequency, and the frequency change is dense, reflecting the high degree of freedom of the large-span indoor sports hall structure.
The results of the first six modal analyses are shown in Fig. 2. It can be seen that the structure experiences horizontal lateral displacement in the first and second modes of vibration, while vertical torsion occurs in the third mode of vibration, indicating that the structural layout is reasonable. The structure is symmetrically distributed, and the horizontal stiffness of the roof structure is evenly distributed throughout. The H-shaped steel columns at the bottom are mainly located at the left and right ends of the main station building area. The number of medium-sized steel columns at the top of the structure is small, so the stiffness is weak, and the displacement may be excessive in the earthquake action. Vertical displacement is an important control parameter for large-span structures.
Table 1The first twenty nature frequency
Order | Nature frequency / Hz | Order | Nature frequency / Hz |
1 | 0.8168 | 11 | 2.4355 |
2 | 0.9612 | 12 | 2.5483 |
3 | 1.1756 | 13 | 2.6152 |
4 | 1.3260 | 14 | 2.6549 |
5 | 1.5620 | 15 | 2.6859 |
6 | 1.6930 | 16 | 2.7114 |
7 | 1.8654 | 17 | 2.7290 |
8 | 2.0965 | 10 | 2.7591 |
9 | 2.1654 | 19 | 2.7826 |
10 | 2.3663 | 20 | 2.8012 |
Fig. 2The first six modal shapes
a) The first order
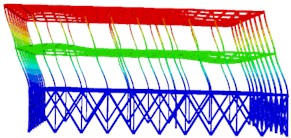
b) The second order
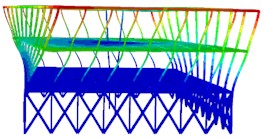
c) The third order
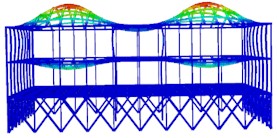
d) The fourth order
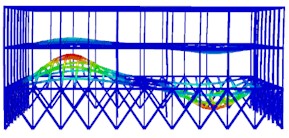
e) The fifth order
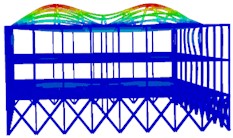
f) The sixth order
2.3. Optimization of rigid connection
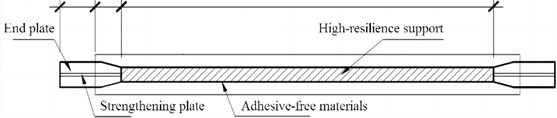
To enhance the seismic resistance of the gymnasium truss structure, additional damping components were added. During isolation, the supports are usually arranged at the top of the support columns, where the support columns are connected to the upper roof structure, to achieve effective amplitude control. By replacing the BRB rod with a large-span truss rod, as shown in Fig. 3, the structure's forces and deformations under seismic action can be effectively controlled. BRB is a displacement-type damping device that utilizes steel deformation to absorb energy, providing both lateral stiffness and additional damping, and without the requirement for long-slender ratio of conventional supports, making the design more flexible and convenient. When subjected to axial compression, the sandwich steel plate will limit the horizontal displacement of the sandwich rubber, and the bearing’s compressive stiffness is extremely high, with almost no axial strain. The steel plate constraint causes the lead core and rubber layer within the bearing to deform in unison. When subjected to horizontal forces, the sandwich steel plate will not limit the shear displacement of the sandwich rubber, and the bearing can still produce shear strain. When a load is applied structurally, the axial load carried by the BRB is determined according to the respective stiffness ratios of the BRB and the conventional load-bearing components, and the yield stiffness of the BRB is determined based on the numerical value of the load. Then, the size of the core material cross-section is determined.
Fig. 3The structure of BRB rod
2.4. Optimization of articulated structure
In order to ensure that the structure is not completely destroyed by a rare earthquake, steel bracings were added to the second and third floors of the steel structure to increase its overall stiffness, with the diagonal brace section selected as an H-shape, as shown in Fig. 4. Before strengthening, the first location where plastic hinges appeared in the steel structure was at the end of the beam connected to the column at the center of the ground floor. The first location where plastic hinges appeared was at the end of the beam in the center of the first-floor span, followed by the appearance of plastic hinges at the end of the beam at the center of the second-floor floor slab. The plastic hinge at the end of the beam at the center of the ground floor appeared earlier than the plastic hinge at the center of the first-floor span, and the plastic hinge at the end of the beam at the center of the ground floor was the first to fail.
Fig. 4The reinforced overall structure
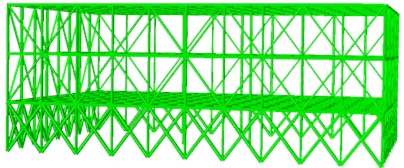
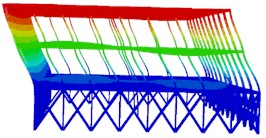
Fig. 5The first six modal shapes of optimized structure
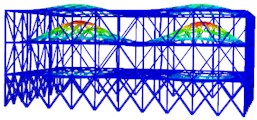
a) The first order
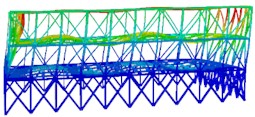
b) The second order
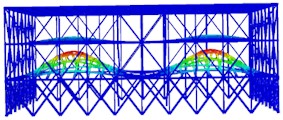
c) The third order
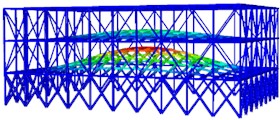
d) The fourth order
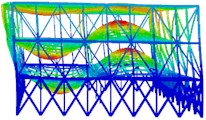
e) The fifth order
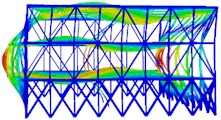
f) The sixth order
2.5. Verification of stiffness characteristics
The modal shapes of the truss after reinforcement are shown in Fig. 5. It can be seen that the vibration displacement of the top layer is significantly reduced at different natural frequencies. Furthermore, from the calculation results of the natural frequencies, it can be known that the fundamental period of the optimized structure is 1.0388 s, which is smaller than the fundamental period of the original structure before reinforcement. The first-order modal frequency is 0.9626 Hz, and the twentieth-order modal frequency is 3.3284 Hz. The self-vibration frequency of the steel structure after reinforcement is greater than that of the steel structure before reinforcement.
3. Simulation and analysis of seismic response
3.1. Selection of seismic waves
The selection of seismic waves is a key factor in determining the accuracy of the time history analysis. According to the seismic code requirements, the Elcentro and Taft natural waves are selected as the seismic sources for analyzing the seismic resistance capacity of the truss, as shown in Fig. 6. Based on the established truss structure finite element model, nonlinear dynamic time history analysis was conducted to statistically analyze the seismic response results. Since the dynamic response patterns of the same structure under different intensity earthquakes are similar, only the seismic response diagrams of the structure under strong earthquakes are listed.
Fig. 6Different seismic waveforms
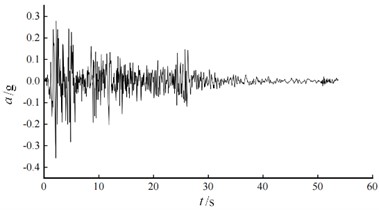
a) El Centro wave
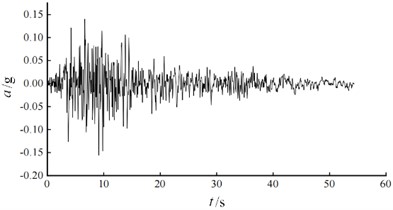
b) Taft wave
Fig. 7Internal forces of the central element under different seismic waves
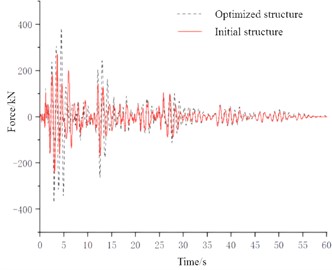
a) Condition of El Centro wave
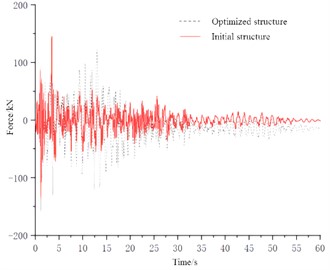
b) Condition of Taft wave
3.2. Comparison of truss internal force responses
Due to the large number of truss structure members, the central element with the largest internal force response and one representative element were selected by comparing the finite element analysis results. The variation pattern of truss internal forces under different seismic wave conditions can be obtained as shown in Fig. 7. The results show that the axial force of the truss unit can be reduced by 25 % to 31 % under the Elcentro wave action, and the truss unit's load is more evenly distributed after the isolation design, with a significant reduction in the peak axial force of the truss unit. Under the Taft wave action, the axial force damping rate is 33 % to 43 %. Compared with the El Centro earthquake wave, the reduction ratio of the peak axial force after structural optimization is greater.
4. Conclusions
1) The basic period of the gymnasium truss structure after increasing stiffness is 1.0388 s, while the natural period of the structure before increasing stiffness is 1.2242 s. The natural period of the structure after increasing stiffness is lower, indicating that the reinforced structure has greater overall stiffness than the structure before reinforcement. From the results of the time history analysis, it can be seen that the steel structure after increasing stiffness has better seismic performance.
2) By using isolation design, the load of the upper roof structure can be more evenly transferred to the lower steel columns, reducing the moment peak value of the lower columns. In different seismic wave conditions, the optimized structure has shown a significant reduction in internal forces. Under the support of optimized structure, the peak axial force of the truss is significantly reduced, and the internal forces can be effectively controlled. Similarly, under the action of earthquakes, the hysteretic curve of the isolation bearing is full and the number of hysteretic cycles is large, which can effectively consume the energy input from earthquakes.
References
-
J. Bergenudd, J.-M. Battini, and R. Crocetti, “Dynamic analysis of a pedestrian timber truss bridge at three construction stages,” Structures, Vol. 59, No. 1, p. 105763, Jan. 2024, https://doi.org/10.1016/j.istruc.2023.105763
-
A. Mena and Z. Volkmar, “Modal identification of structures with a dynamic behaviour characterised by global and local modes at close frequencies,” Acta Mechanica, Vol. 235, No. 3, pp. 1471–1491, May 2023, https://doi.org/0.1007/s00707-023-03598-z
-
J. Guo, G. Wei, X. Li, D. Jin, and F. Liu, “Modal identification of structures with closely spaced modes based on improved empirical wavelet transform,” Journal of Vibration Engineering and Technologies, Vol. 10, No. 7, pp. 2625–2640, Apr. 2022, https://doi.org/10.1007/s42417-022-00508-w
-
J. Freundlich and D. Sado, “Dynamics of a mechanical system with a spherical pendulum subjected to fractional damping: analytical analysis,” Nonlinear Dynamics, Vol. 111, No. 9, pp. 7961–7973, Feb. 2023, https://doi.org/10.1007/s11071-023-08269-1
-
M. S. Miah, “Vibration mitigation of high-rise buildings via tuned mass damper subjected to dynamic loads,” in IOP Conference Series: Materials Science and Engineering, Vol. 1070, No. 1, p. 012031, Feb. 2021, https://doi.org/10.1088/1757-899x/1070/1/012031
-
M. El Hoseny, J. Ma, and M. Josephine, “Effect of embedded basement stories on seismic response of low-rise building frames considering SSI via small shaking table tests,” Sustainability, Vol. 14, No. 3, p. 1275, Jan. 2022, https://doi.org/10.3390/su14031275
About this article
The authors have not disclosed any funding.
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
The authors declare that they have no conflict of interest.
