Structural design and dynamic characteristic analysis of adjustable badminton serving machine

2.1. The overall design of structure and function

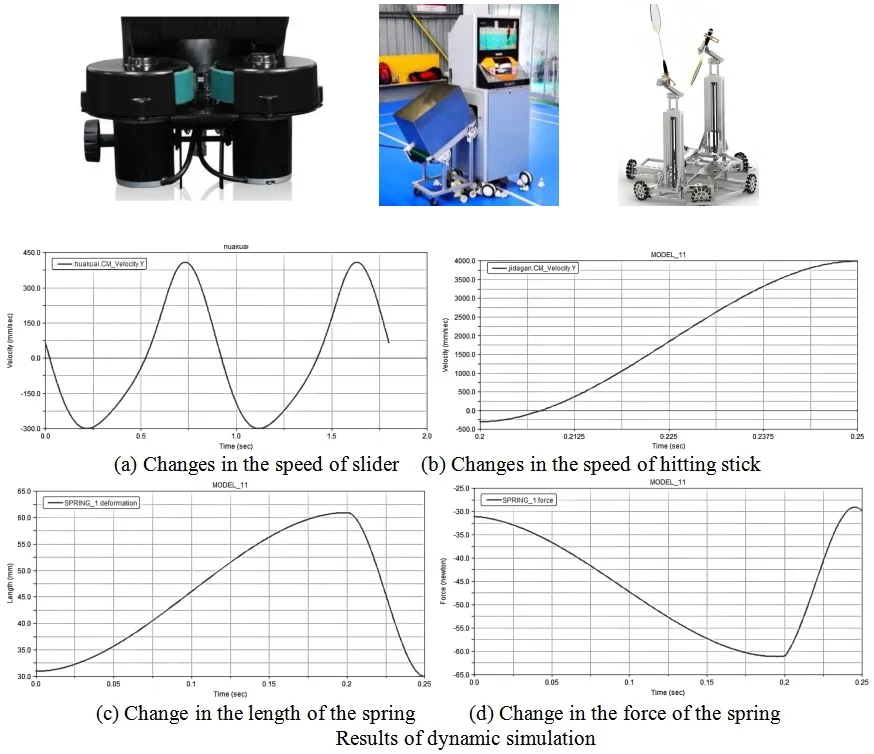
There are primarily three categories of badminton serving machines available in the current market. As shown in Fig. 1(a), the first type of badminton serving machine is using high-pressure gas. This structure requires a larger size and an air compressor to compress air and shoot the badminton out. However, this method is less commonly used due to its high cost, complex operation, high power consumption, high noise levels, and other factors. As shown in Fig. 1(b), the second type of badminton serving machine discards the traditional ball clamping mechanism and instead uses a conveyor belt to sort and transport the balls to the serving area. The entire ball machine functions as a complete automated device. However, this equipment is not suitable for individual purchase, as it is quite large in size and weighs nearly 160 pounds. As shown in Fig. 1(c), the third type of badminton serving machine is capable of simulating human hitting actions, featuring high automation and excellent controllability. However, the overall manufacturing cost is relatively high, and it demands a higher level of court flatness, making it unsuitable for courts with limited resources.

Fig. 1Common badminton serving machine

a) Pneumatic transmission structure

b) Large storage structure

c) Hitting structure

Fig. 2The main structural composition: 1 – storage location; 2 – ball platform; 3 – vertical guide rail; 4 – slider; 5 – crank; 6 – guide bar; 7 – hinge seat; 8 – disc CAM; 9 – roller follower; 10 – connecting rod; 11 – horizontal guide rail

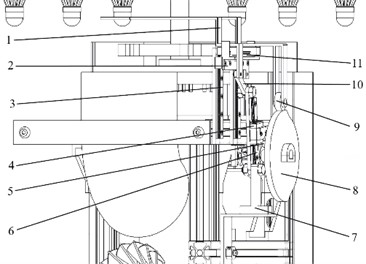
In order to design a cost-effective, compact, and less site-dependent badminton serve machine that is suitable for individual purchase and use, the striking ball launching mechanism designed in this paper adopts a biased crank-slider mechanism, a stretched spring, and an electromagnet in combination. As shown in Fig. 2, the ball launching mechanism is based on the principle of firearms. The designed structure adopts a combination of swing guide rod mechanism, cam mechanism, and ball retrieval device. The motor can drive the disc-shaped cam to rotate, and the roller follower moves up and down along the outer contour of the disc-shaped cam, thereby driving the ball retrieval hand platform to perform vertical reciprocating motion along the vertical guide rail, thus achieving the action of pulling down the badminton ball. The horizontal guide rail is installed on the ball retrieval hand platform, and the vertical guide rail is fixedly connected to the frame. The swing guide rod mechanism consists of a crank, guide rod, linkage, hinge seat, and slider, where the crank is installed at one end on the slider and at the other end on the cam, the slider is installed on the guide rod, one end of the guide rod is fixedly connected to the hinge seat, and the other end is connected to the linkage, the other end of the linkage is fixedly connected to the ball retrieval hand, and the ball retrieval hand moves along the horizontal guide rail under the action of the swing guide rod mechanism, thereby achieving the action of clamping and releasing the badminton ball.

2.2. Design of key actuating mechanisms

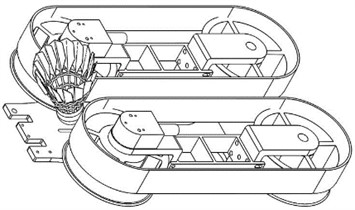
The electromagnet ball fetcher needs to install the electromagnet on the outside of the ball storage barrel, which will cause the volume of the ball storage barrel to be too large and affect the number of the ball storage barrel of the ball storage mechanism. Therefore, it has certain limitations, so the pinch-type ball fetching mechanism is adopted, as shown in Fig. 3. The launch mechanism, as shown in Fig. 4, uses a friction double-wheel launching mechanism. The principle is to accelerate the badminton ball by applying pressure to its badminton and feather parts through two friction wheels rotating around the motor axis, which are driven by two motors. The launching speed is achieved by adjusting the speed of the friction wheels.

The pneumatic serving mechanism primarily utilizes an air compressor to compress air, and a positioning pre-tension device to secure the badminton. Badminton is struck by ejecting high-pressure gas through the ejection nozzle, thereby launching the badminton by striking the interior of the badminton head. The serving speed can be adjusted by regulating the gas pressure in the ejection nozzle. The composition of the actuating mechanism is shown in Fig. 5. When the electromagnet is energized, the slider attracts the striking rod, and the slider, driven by the motor, moves to the right with the striking rod. At the same time, the stretched spring stretches and accumulates energy, moving to the designated position when the electromagnet loses power, the slider separates from the striking rod. The striking rod, driven by the stretched spring, accelerates and strikes the head of the badminton ball, completing the ball launching action. The striking force can be controlled by controlling the stretching amount of the stretched spring, thereby controlling the ball launching speed. Because the contact time between the racket and the badminton is very short, the average force between them is larger, and the external force applied is approximately zero, therefore, the process of hitting the badminton can be considered as a collision problem of momentum conservation.

Fig. 3Ball fetching mechanism

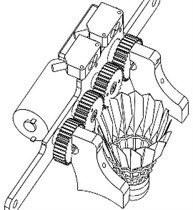
Fig. 4Ball launching mechanism

2.3. Dynamic simulation of serve mechanism

According to the designed mechanical structure, dynamic model simulation was carried out. Interactive simulation was chosen, with a step size set to 1000 steps and a simulation time set to 1.8 seconds. The parameters of stretch spring damper are set according to the actual selection of parts. The stiffness coefficient is set to 3.0 and the damping coefficient is set to 0.03. Since the batting rod needs to collide with the badminton ball to complete the serving action, the contact force is set between the batting rod and the badminton ball.

Fig. 5The composition of the actuating mechanism: 1 – badminton; 2 – stretch spring; 3 – bat; 4 –electromagnet; 5 – slide block; 6 – crankshaft; 7 – coupling; 8 – motor; 9 – rail; 10 – linkage; 11 – serving tube

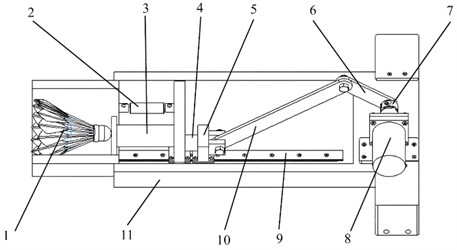
Fig. 6Results of dynamic simulation

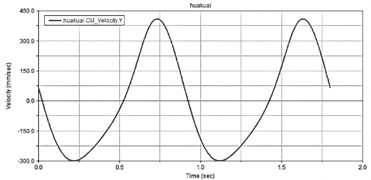
a) Changes in the speed of slider

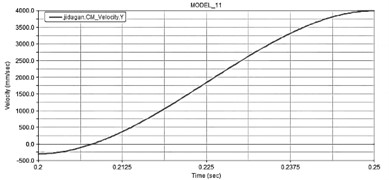
b) Changes in the speed of hitting stick

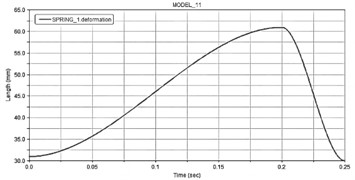
c) Change in the length of the spring

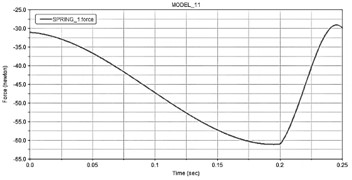
d) Change in the force of the spring

After completing the dynamic simulation, the time-domain variation curves of the slider, hitting stick, and spring were obtained through the ADAMS/Processor post-processing module, as shown in Fig. 6. According to the analysis results, the slider moves in a linear back-and-forth motion, with a period of about 0.9 seconds and a slider travel of about 90 mm. The peak and trough points of the displacement curve are the left and right extreme positions of the eccentric crank slider mechanism. When the slider velocity curve is zero, it corresponds to the left and right two extreme positions of the slider, at which the slider acceleration reaches the maximum reverse value, which changes within the range of –3000 to 2500. The maximum velocity of the slider’s working stroke is smaller than the maximum velocity of the return stroke, proving that the eccentric crank slider mechanism has a rapid return characteristic. The mechanism runs smoothly without impact, and the values of slider travel, velocity, and acceleration meet the design requirements. The striking rod first moves to the right extreme position under the action of the eccentric crank slider mechanism and the solenoid, stretching the spring. When the striking rod moves to the maximum stretching length of the spring, 30 mm, at this time the solenoid loses power, and the striking rod separates from the slider. Under the action of the two stretched springs with a total force of 124 N, the striking rod moves to the left direction and collides with the badminton, completing the serving action, which verifies the correctness of the serving mechanism design.

3.1. Aerodynamic motion equation

Badminton is mainly influenced by gravity, air resistance, and buoyancy during the stable flight stage. Air resistance is mainly composed of three parts: frontal resistance, frictional resistance, and vortex resistance. The frontal resistance is the force that the badminton receives when it flies forward, and its direction is opposite to the direction of the badminton’s forward flight. The size of the resistance is related to the flight speed and air density. Due to the viscosity of air, a layer of air will adhere to the surface of the badminton, and the speed of the air layer is the same as the flight speed of the badminton, thus slowing down the flight speed of the badminton. According to the Yi-Hsiang theory, the aerodynamic motion equation of a badminton can be derived as follows:

where $v_t$ is instantaneous velocity, $g$ is gravitational acceleration, $t$ represents time, $x$ and $y$ represent the horizontal and vertical directions.

The flight trajectory of a badminton is determined by the initial conditions and the forces acting on the badminton in the air. There are many factors that affect the initial conditions of a badminton. Under the assumption that the badminton does not rotate or deviate sideways, the aerodynamic motion equation established can be used to simulate the flight trajectory and investigate the impact of three initial conditions, namely, the initial velocity, the initial pitch angle, and the initial height, on the flight trajectory. This provides a theoretical basis for setting the launch parameters of a badminton launcher.

3.2. The influence of working parameters on the motion trajectory

Under different working parameters, the flight trajectory of a badminton can be obtained as shown in Fig. 7. When a badminton is launched at a certain speed, in the vertical direction, in the upward stage, the badminton first flies at its terminal velocity for a certain period of time, then its speed gradually decreases to zero under the influence of gravity and air resistance. In the downward stage, the badminton is curved downwards rapidly under the action of gravity, almost reaching the tangent line at a vertical angle.

As the flight speed increases, the air resistance on the badminton also gradually increases. When the gravity equals the air resistance, the badminton will fall at a constant speed. Therefore, the time it takes for the badminton to fall is much shorter than the time it takes to rise, and the slope of the falling stage is greater than that of the rising stage. In the horizontal direction, the badminton is only affected by air resistance, and it performs an accelerating motion with a gradually decreasing speed. When the launch angle increases, the vertical component of the air resistance will decrease, making the badminton fly higher and fall more quickly. However, changing the launch height has no effect on the badminton's landing point, but it will shift the entire flight trajectory upwards. The flight trajectory of the badminton is determined by the launch angle and initial speed, and is independent of the height.

Fig. 7Trajectories at different working parameters

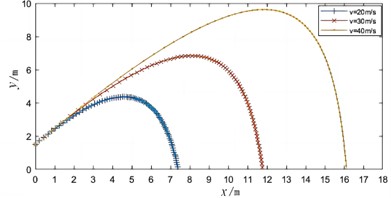
a) Trajectories at different initial velocity

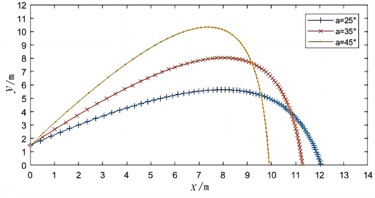
b) Trajectories at different pitch angle

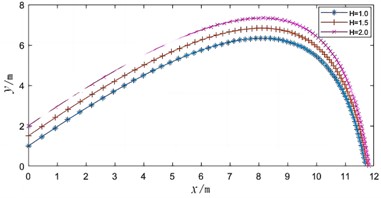
c) Trajectories at different initial height