Abstract
The article experimentally investigated unsteady-state creep of a hot fine-grained dense asphalt concrete under uniaxial tension at temperatures of 22-24 °C. 61 samples of the asphalt concrete in the form of a rectangular beam with dimensions of 50×50×150 mm were tested to complete failure at seven different stresses (from 0.084 MPa to 0.3053 MPa) in a special installation with a heat chamber. Based on the test results, unsteady-state creep curves were constructed, which were normalized and approximated with high accuracy by a power function. Reliable dependences of the limiting time of hardening, the limiting strain of hardening, and the hardening rate on stress have been established.
Highlights
- The unsteady-creep of an asphalt concrete measured and approximated.
- New parameters of the unsteady creep are introduced: the limiting time of hardening, the limiting strain of hardening and the hardening rate.
- Dependences of the limiting time of hardening, the limiting strain of hardening and the hardening rate on stress have been established.
1. Introduction
The deformability and strength of many materials, including road asphalt concretes, depend on temperature, magnitude and duration of load. A well-known and effective way to assess the influence of these factors on materials is to test them for creep [1, 2].
Systematic studies of creep of asphalt concretes began in the 70s of the last century [3]. In works [4-7] it was shown that asphalt concretes have three stages of creep (unsteady-state, steady-state and accelerated) and it was proposed to describe these stages separately mathematically. In articles [8, 9], the steady-state creep of an asphalt concrete was studied in detail. The works of A. Iskakbayev, B. Teltayev et all. [4, 6, 10] are devoted to the experimental study and mathematical description of unsteady creep of the asphalt concrete. Moreover, in article [4], unsteady-state creep of the asphalt concrete is mathematically described by the Rabotnov’s fractional exponential function [11], and in articles [6,10] - by the Abel kernel. More detailed and extended studies of unsteady-state creep of the asphalt concrete were carried out in [12].
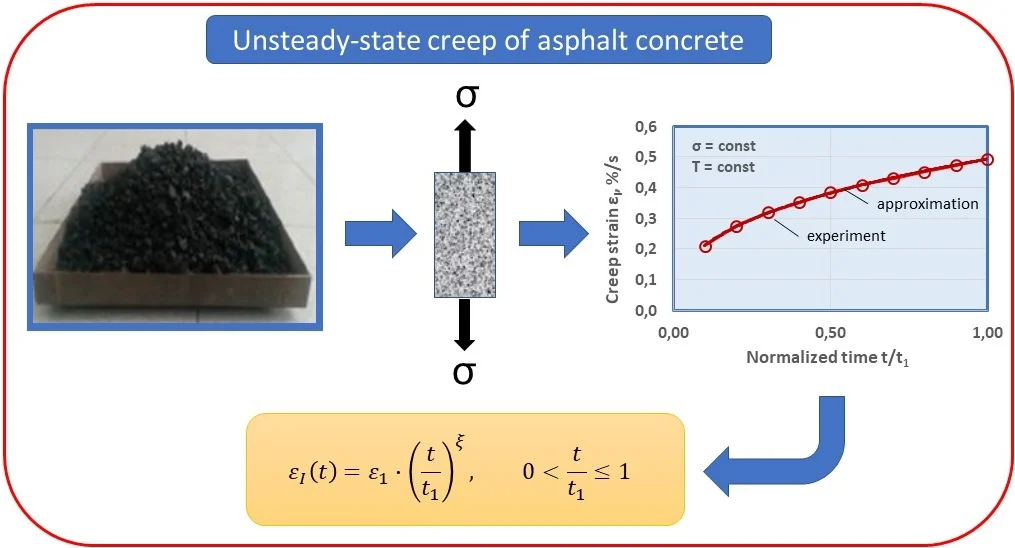
In this article, the unsteady-state creep of the asphalt concrete under uniaxial tension at temperatures of 22-24°C is studied in more depth: a normalized time is introduced; the strain is described by a simple power function; the terms of “limiting time of hardening”, “limiting strain of hardening” and “hardening rate” were introduced, and their dependences on stress were established.
2. Materials and methods
2.1. Materials
A hot fine-grained dense asphalt concrete of type B, meeting the requirements of the standard ST RK 1225-2013 [13], was prepared using a bitumen of grade BND 100-130, obtained at the Pavlodar petrochemical plant and meeting the requirements of the standard ST RK 1373-2013 [14]. Composition of the asphalt concrete: crushed stone – 43 % (5-10 mm – 20 %, 10-15 mm – 13 %, 15-20 mm – 10 %), sand – 50 %, mineral powder – 7 %; bitumen - 4.8 % [3, 6].
2.2. Sample preparation
The asphalt concrete samples in the shape of a rectangular beam with dimensions of 50×50×150 mm were made as follows. First, the asphalt concrete samples were prepared in the form of a slab with dimensions of 350×350×50 mm according to the standard EN 12697-33-2003 [15], which were then cut into the above beams.
2.3. Testing
The asphalt concrete samples (beams) were tested for creep under uniaxial tension at temperatures of 22-24 °C until complete failure at different stresses (from 0.084 to 0.3053 MPa). In individual tests, temperature and stress were kept constant throughout the experiment. The tests were carried out in a special installation with a heat chamber [3, 6]. 61 asphalt concrete samples were tested at seven different stresses. The elongation of the samples over time was measured by two indicators of a clock type and recorded with a video camera, which were then processed and analyzed.
3. Results and discussions
3.1. Unsteady-state creep curves
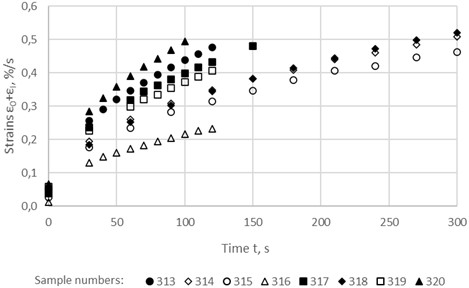
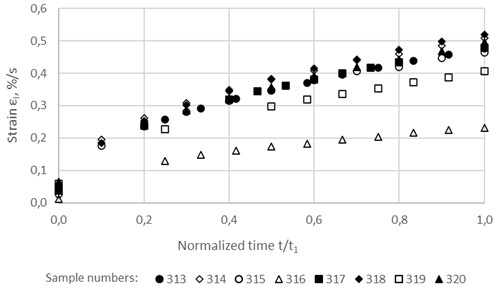
The unsteady-state creep curves of the asphalt concrete samples at two stresses (0.084 MPa and 0.1852 MPa), constructed from the test results, are shown in Fig. 1 and 2. It can be seen that the curves of parallel samples are characterized by significant heterogeneity; All characteristics are very different: conditionally instantaneous strain εо, unsteady-state creep strains εI(t), limiting strain of hardening ε1 and limiting time of hardening t1.
Fig. 1Unsteady-state creep curves of the asphalt concrete samples at a stress of 0.084 MPa
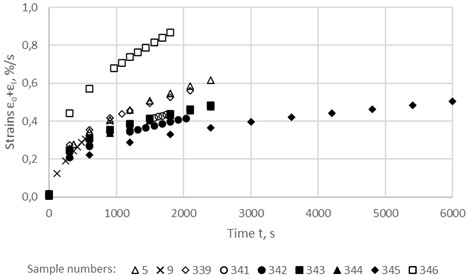
Fig. 2Unsteady-state creep curves of the asphalt concrete samples at a stress of 0.1852 MPa
Normalized versions of these curves are presented in Fig. 3 and 4, in which time is normalized in relation to the limiting time of hardening, i.e. time t is replaced by the ratio t/t1. The conditionally instantaneous strain εо is excluded from all curves, i.e. all creep curves represent only unsteady-state creep strains and have a zero value at t=0.
Fig. 3Normalized unsteady-state creep curves of the asphalt concrete samples at a stress of 0.084 MPa
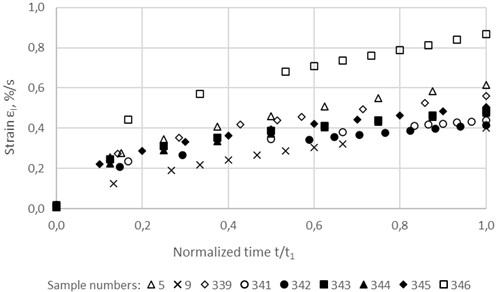
Fig. 4Normalized unsteady-state creep curves of the asphalt concrete samples at a stress of 0.1852 MPa
3.2. Approximation of unsteady-state creep curves
As noted in the introductory part of the article, the creep curve of an asphalt concrete is divided into three characteristic sections. Then the entire creep curve can be represented by the following expression:
where εо – conditionally instantaneous strain; εI(t), εII(t), εIII(t) – unsteady-state, steady-state and accelerated creep strains, respectively.
In this article, the unsteady-state creep of the asphalt concrete is approximated by a power function of the following form:
where ε1 – limiting strain of hardening, ε1=εI(t1), %; t1 – limiting time of hardening, i.e. duration of unsteady-state creep, s; ξ – hardening rate.
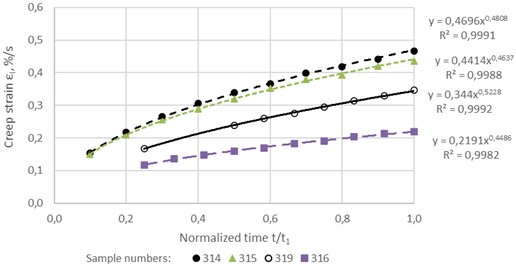
As illustrative examples, Figs. 5-6 show the experimental values of strain of the asphalt concrete samples and the corresponding approximating curves. As you can see, the degree of approximation accuracy is very high: the values of the reliability indicators (R2) range from 0.9988 to 0.9999. And for all the remaining 53 samples, an approximation of the same high degree was obtained: R2min=0,9347; R2max= 1.
Fig. 5Approximation of unsteady-state creep curves of two samples (No. 5, 9, 343 and 346) of the asphalt concrete at a stress of 0.084 MPa
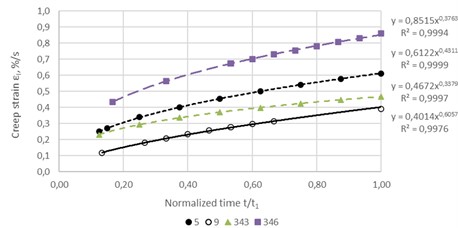
Fig. 6Approximation of unsteady-state creep curves of two samples (No. 314, 315, 316 and 319) of the asphalt concrete at a stress of 0.1852 MPa
3.3. Characteristics of unsteady-state creep
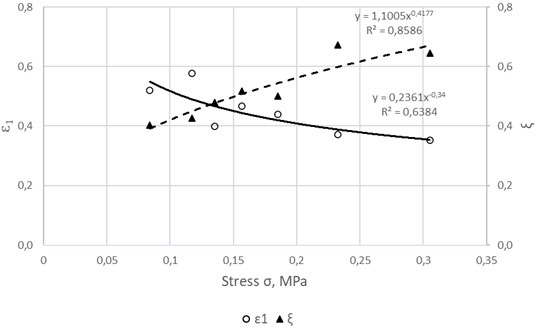
Important characteristics of unsteady-state creep of materials are the limiting time of hardening, limiting strain of hardening, and hardening rate. For the studied asphalt concrete, the dependences of these characteristics on stress are shown in Figs. 7-8.
Fig. 7Dependence of limiting time of hardening on stress
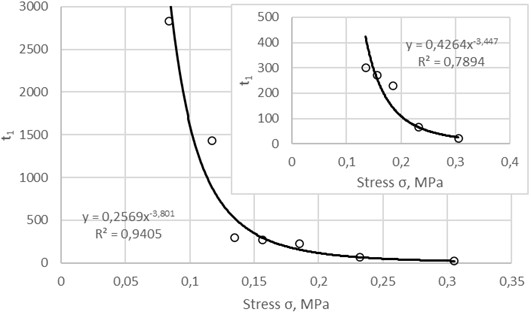
It can be seen that all of these dependencies are described with high accuracy by a power function. The most sensitive characteristic to changes in stress turned out to be the limiting time of hardening t1. At a stress of 0.084 MPa, the value of t1 is equal to 2826 s, and at stresses of 0.135 MPa and 0.3053 MPa it is equal to 300 s and 20.62 s, respectively, i.e. with an increase in stress by 1.6 and 3.6 times, t1 decreases by almost 10 and 140 times, respectively.
The limiting strain of hardening ε1 and the hardening rate ξ turned out to be relatively weakly dependent on stress. Thus, with an increase in stress by 3.63 times in the range from 0.084 MPa to 0.3053 MPa, ε1 decreases by 1.5 times, and ξ increases by 1.6 times.
Fig. 8Dependence of limiting strain of hardening on stress
4. Conclusions
Unsteady-state creep curves are approximated with high accuracy by a power function.
The most sensitive characteristic to changes in stress is the limiting time of hardening t1; with an increase in stress by 1.6 times (from 0.084 MPa to 0.135 MPa) and 3.6 times (from 0.084 MPa to 0.3053 MPa), t1 decreases by 10 times and 140 times, respectively.
The limiting strain of hardening ε1 and the hardening rate ξ weakly depend on stress: with an increase in stress by 3.6 times (from 0.084 MPa to 0.3053 MPa), ε1 decreases by 1.5 times, and ξ increases by 1.6 times.
References
-
Y. N. Rabotnov, “Calculation of machine parts for creep,” (in Russian), News of the USSR Academy of Sciences. Department of Technical Sciences, 1948.
-
Y. N. Rabotnov, Mechanics of Deformed Solid. (in Russian), Moscow: Nauka, 1988.
-
A. I. Iskakbayev, B. B. Teltayev, K. Z. Yestayev, and B. D. Abu, “Long-term strength of asphalt concrete and its applications,” Construction and Building Materials, Vol. 244, p. 118325, May 2020, https://doi.org/10.1016/j.conbuildmat.2020.118325
-
A. Iskakbayev, B. Teltayev, and S. Alexandrov, “Determination of the creep parameters of linear viscoelastic materials,” Journal of Applied Mathematics, Vol. 2016, pp. 1–6, Jan. 2016, https://doi.org/10.1155/2016/6568347
-
A. Iskakbayev, B. Teltayev, F. Andriadi, K. Yestayev, E. Suppes, and A. Iskakbayeva, “Experimental research of creep, recovery and fracture processes of asphalt concrete under tension,” in Proceedings of the 24th International Congress on Theoretical and Applied Mechanics, Aug. 2016.
-
B. B. Teltayev, A. Iskakbayev, and C. Oliviero Rossi, “Regularities of creep and long-term strength of hot asphalt concrete under tensile,” in 4th Chinese-European Worshop “Functional Pavement Design”, Oct. 2016, https://doi.org/10.1201/9781315643274-19
-
A. I. Iskakbayev, B. B. Teltayev, and C. O. Rossi, “Deformation and strength of asphalt concrete under static and step loadings,” in Transport Infrastructure and Systems, Mar. 2017, https://doi.org/10.1201/9781315281896-1
-
A. Iskakbayev, B. Teltayev, and C. Oliviero Rossi, “Steady-state creep of asphalt concrete,” Applied Sciences, Vol. 7, No. 2, p. 142, Feb. 2017, https://doi.org/10.3390/app7020142
-
B. B. Teltayev, A. I. Iskakbayev, and B. D. Abu, “Steady-state deformation of asphalt concrete,” Construction and Building Materials, Vol. 349, p. 128754, Sep. 2022, https://doi.org/10.1016/j.conbuildmat.2022.128754
-
Iskakbayev A. I., Teltayev Bagdat Burkhanbaiuly, Yensebayeva G. M., and Kutimov K. S., “Computer modeling of creep for hereditary materials by Abel’s kernel,” News of National Academy of Sciences of the Republic of Kazakhstan, Vol. 6, No. 432, pp. 66–76, Dec. 2018, https://doi.org/10.32014/2018.2518-170x.36
-
Y. N. Rabotnov, Elements of Hereditary Mechanics of Solids. (in Russian), Moscow: Nauka, 1977.
-
B. Teltayev, A. Iskakbayev, C. Oliviero Rossi, and B. Abu, “Unsteady-state creep of an asphalt concrete,” Applied Sciences, Vol. 12, No. 3, p. 1615, Feb. 2022, https://doi.org/10.3390/app12031615
-
“Hot mix asphalt for roads and airfields. Technical specifications,” (in Russian), Astana, Technical specifications, ST RK 1225-2013, 2013.
-
“Bitumen and bitumen binders. Oil road viscous bitumens. Technical specifications,” (in Russian), Astana, Technical specifications, ST RK 1373-2013, 2013.
-
“Bituminous mixtures. Test methods for hot mix asphalt. Part 33. Specimen prepared by roller compactor,” European committee for standardization, Brussels, EN 12697-33-2003, 2003.
About this article
The authors would like to express their sincere gratitude for the financial support provided by the Fundamental Research Grant from the Ministry of Science and Higher Education of the Republic of Kazakhstan (Grant Number: BR20280990) to U. Joldasbekov IME.
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
The authors declare that they have no conflict of interest.

