Influence of asphalt mixture nonlinearity on pavement mechanical response

1. Introduction

Asphalt mixture is a composite material consisting of asphalt, coarse aggregates, and fine aggregates. It is a typical viscoelastic material, and its performance is closely related to load, temperature, and the duration of load application. Traditional studies have treated asphalt mixtures as linear viscoelastic materials, using linear viscoelastic constitutive equations to study their performance, such as the Huet model [1], 2S2P1D model [2], generalized Kelvin model [3], and others. Similarly, in the study of the mechanical response of asphalt pavement structures, the properties of linear viscoelastic materials are often incorporated into layered viscoelastic systems or finite element viscoelastic analyses [4-6]. However, numerous studies have shown that asphalt mixtures are nonlinear viscoelastic materials [7-9], with material properties exhibiting stress dependency.

Therefore, this paper first conducts research on the creep properties of asphalt mixtures under different loading conditions in the laboratory. Then, by establishing the conversion relationship between viscoelastic creep compliance and relaxation modulus, the conversion of relaxation modulus is accomplished. Finally, the relaxation modulus is applied to the mechanics of layered viscoelastic systems to analyze the influence of asphalt mixture nonlinearity on the mechanical response of asphalt pavement structures, aiming to clarify the significance of asphalt mixture nonlinearity in pavement structure design.

2. Uniaxial creep test

3. Study of viscoelastic parameters of asphalt mixtures

3.1. Asphalt mixture creep compliance under different loading conditions

Axial displacements of asphalt mixtures under various loads were measured using a UTM (Universal Testing Machine). Subsequently, axial strain values at different time intervals under different loading conditions were obtained using Eq. (1):

1

$\epsilon \left(t\right)=\frac{\mathrm{\Delta }l}{l},$

2

$J\left(t\right)=\frac{\epsilon \left(t\right)}{{\sigma }_0}.$

Based on the calculation method for creep compliance, the creep compliance values of asphalt mixtures under different loading conditions were determined, as shown in Fig. 1.

Fig. 1Asphalt mixture creep compliance under different loads

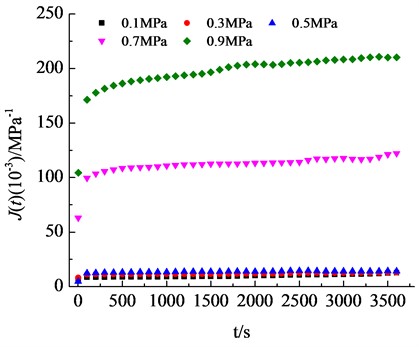
As shown in the figure, the creep compliance of the asphalt mixture gradually increases with an increase in time. However, the creep compliance tends to stabilize at a constant value after a certain time period. When the load is in the range of 0.1 to 0.5 MPa, the creep compliance of the asphalt mixture is approximately consistent, which indicates that the asphalt mixture behaves as a linear viscoelastic material within the load range of 0.1 to 0.5 MPa. However, at load levels of 0.7 MPa and 0.9 MPa, the creep compliance of the asphalt mixture increases significantly, being 5 times and 10 times greater than that at lower loads. This suggests that the asphalt mixture is in a nonlinear phase at these load levels. The Curve Fitting Toolbox in MATLAB was utilized to perform Prony series fitting for creep compliance under different loads. The Prony series is expressed as Eq. (3), and the parameters ${\tau }_i$ of the Prony series are provided in Table 4, the parameters $J_i$ values of the Prony series are provided in Table 4:

3

$J\left(t\right)=J_0+\sum _{i=1}^7{J}_i\left(1-e^{-\frac{t}{{\tau }_i}}\right).$

Table 4Parameter τivalues

	1	2	3	4	5	6	7
${\mathrm{\tau }}_{\mathrm{i}}$	0.001	0.01	0.1	1	10	100	1000

Table 5Parameter values of creep compliance Prony series of asphalt mixtures under different loads

$J_i$	Loads (MPa)
	0.1	0.3	0.5	0.7	0.9
$J_0$	0.925	1.123	1.252	1.532	1.645
$J_1$	0.3273	1.877	2.433	13.46	23.02
$J_2$	1.393	1.939	2.407	13.32	23.38
$J_3$	1.278	1.564	1.92	13.2	23.37
$J_4$	1.568	1.305	0.5098	17,27	22.2
$J_5$	1.727	2.873	3.736	35.15	74.92
$J_6$	0	0	0.0001916	7.075	0
$J_7$	3.788	1.781	2.037	16.26	40.6
*Considering the form of (3), values of $J_i$ less than 10-5 are treated as zero

3.2. Conversion of creep compliance to relaxation modulus

In the calculations of mechanical responses for asphalt pavement structures, modulus is used as an input parameter. Therefore, it is necessary to convert creep compliance into relaxation modulus. Research on the conversion of viscoelastic parameters for asphalt and asphalt mixtures primarily focuses on the conversion between creep compliance and relaxation modulus. Xue et al. [10] used BBR tests to measure the creep compliance of asphalt, and then discretized the creep compliance in the time domain, and calculated the relaxation modulus using the convolution relationship in the time domain between creep compliance and relaxation modulus, as shown in Eq. (4):

4

${\int }_0^{t}E(t-\tau )J\left(\tau \right)d\tau =t,$

5

$E\left(\frac{t_n+t_{n-1}}{2}\right)=\frac{2t_n-\sum _{i=1}^{n-1}E\left(\frac{t_i+t_{i-1}}{2}\right)\left(J\left(t-t_i\right)+J\left(t-t_{i-1}\right)\right)\left(t-t_{i-1}\right)}{\left(J\left(0\right)+J\left(t_n-t_{n-1}\right)\right)\left(t_n-t_{n-1}\right)},$

where, $E\left(\frac{t_0+t_1}{2}\right)=\frac{2}{J\left(0\right)+J\left(t_1\right)}.$

Similarly, Yan and Wang [11] also used this method to calculate the relaxation modulus of asphalt mixtures using creep compliance. Andmany countries also used this method for parameter conversion of viscoelastic materials in the early stages [12-13]. However, this method requires the discretization of creep compliance in the time domain, which resulted into some errors in the backcalculation of relaxation modulus. Lvet al. [14] employed the calculation relationship in Eq. (4) to determine the parameter values in the expression for relaxation modulus, and established an expression for the relaxation modulus of asphalt mixtures based on the viscoelastic constitutive equation for asphalt mixtures.

This paper employs the method proposed by Tschoegl [15] to perform the conversion between creep compliance and relaxation modulus. The specific conversion formula is as follows. And the calculating result is shown in Fig. 2.

Fig. 2The relaxation modulus of asphalt mixture under different loads

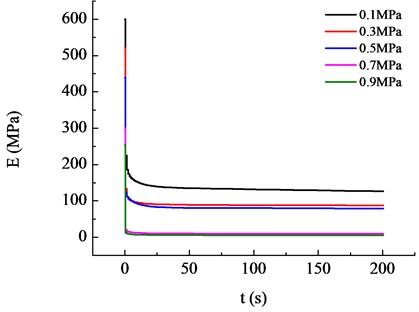
From Fig. 2, it can be observed that the relaxation modulus decreases continuously with an increase in loading time. Additionally, it is evident that the relaxation modulus values tend to become two-digit numbers under the influence of high temperatures (40 °C) and high loads (0.7 MPa, 0.9 MPa). This phenomenon is also consistent with the findings in the studies of Huang et al. [16] and Lvet al. [14]. Furthermore, it can be noted that the magnitude of the load significantly affects the relaxation modulus of the asphalt mixture.

4. Study of asphalt pavement mechanical response

From the findings in the previous section, it is evident that the magnitude of the load has a significant impact on the relaxation modulus of the asphalt mixture. In the 2017 edition of China’s Asphalt Pavement Structural Design Code, the dynamic modulus of the asphalt mixture is used as a material parameter for analysis in the context of layered elastic systems to study asphalt pavement structural behavior. On one hand, this design approach does not consider the viscoelastic properties of the asphalt mixture, especially during high-temperature seasons. On the other hand, the vertical load decreases gradually in the depth direction of the asphalt pavement under vehicle loads. This implies that the modulus at different positions within the asphalt pavement structure are not equal.

The American Empirical Mechanics Method [17] points out that different driving speeds result in different load frequencies within the pavement structure. Referring to the research findings of Zhao et al. [18-19], a driving frequency of 10 Hz is adopted, which is corresponding to a vehicle time of 0.1 seconds. Thus, the vehicle load is represented as a semi-sinusoidal load, with the load function defined as shown in Eq. (6) and Fig. 3:

The load function is incorporated to multilayered viscoelastic mechanics after undergoing Laplace transformation.

Fig. 3Half sine wave load diagram

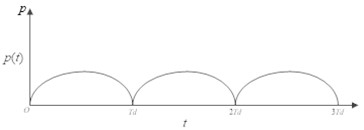
To analyze the impact of nonlinear load variations on the mechanical response of asphalt pavement under different conditions, the pavement structure combinations and parameters used are outlined in Table 6. The asphalt layer is divided into three layers, with the modulus values for each layer as specified in Table 7.

The analysis focuses on the permanent deformation of the asphalt surface layer at the end of loading and the tensile stresses at the bottom of the semi-rigid base layer during the loading process. The calculation results are presented in Table 8.

From Table 8, it can be observed that the nonlinearity of the asphalt mixture has a relatively minor impact on the tensile stress at the bottom of the semi-rigid base layer, indicating minimal influence on the base layer's fatigue performance. However, it significantly affects the permanent deformation of the asphalt layer [20]. In case one, the permanent deformation of the asphalt layer is five times that of case three, and the permanent deformation of the asphalt layer of case two is twice that of case three.

5. Conclusions

The specific conclusions are as follows:

1) The magnitude of the load significantly affects the creep compliance of asphalt mixtures. For AC-16 mixtures, the creep compliance of asphalt mixtures remains roughly the same under loads ranging from 0.1 to 0.5 MPa, which indicates that the material behaves within the linear viscoelastic region. However, when the load exceeds 0.5 MPa, the creep compliance increases significantly, which indicates the material's entry into the nonlinear viscoelastic region.

2) Through the convolution formula between relaxation modulus and creep compliance, relaxation modulus conversion was accomplished. The relaxation modulus of asphalt mixtures decreased rapidly initially and eventually stabilized under high-temperature and high-load conditions. The calculation results also demonstrated that the magnitude of the load significantly influences the relaxation modulus of asphalt mixtures.

3) The nonlinearity of asphalt mixtures has a minor impact on base layer fatigue cracking but significantly affects the permanent deformation of the asphalt layer. In asphalt pavement structural design, attention should be given to the influence of material nonlinearity caused by vehicle axle loads on pavement permanent deformation.