Enhanced diagnostic method for rolling bearings using time-reassigned multi-synchro squeezing transform

2.1. Time-reassigned synchro squeezing transform

In this section, we first briefly introduce the theoretical basis of the TSST [24]. A single-component signal with varying frequency can be described in Eq. (1):

where, $A\left(\omega \right)$ and $\phi \left(\omega \right)$ represent the amplitude and phase of the signal in the frequency domain, while $-{\phi }^{\text{'}}\left(\omega \right)$ denotes the group delay (GD). When a signal is represented in the time-frequency domain, the Ideal Time-frequency Representation (ITFR) can be expressed as Eq. (2):

where, $\delta \left(\right)$ represents the Dirac delta function. According to Eq. (2), ideally, the time-frequency characteristics of a signal should only appear on the GD trajectory. The STFT can be used to extend the signal given by Eq. (1) into the time-frequency domain. In the frequency domain, the STFT of signal $\widehat{g}\left(\xi \right)$ using a moving window function can be expressed as Eq. (3):

Assuming that the analyzed signal exhibits slow frequency variations, which implies that the magnitude of $\exists \mathit{\epsilon }$ is sufficiently small, and given that $\forall \omega$ satisfies conditions $\left|A\text{'}\left(\omega \right)\right|\le \epsilon$ and $\left|\phi \text{'}\text{'}\left(\omega \right)\right|\le \epsilon$, it is possible to derive a first-order expansion of the signal. This expansion provides a simplified representation of the signal’s behavior, capturing its essential characteristics in the time-frequency domain. The first-order approximation allows for a more tractable analysis while preserving key information about the signal's dynamics, as show in Eq. (4):

Substituting Eq. (4) into Eq. (3), we can obtain:

where, $g\left(t\right)$ represents the window function in the time domain. According to Eq. (5), the time-frequency energy propagates along the GD trajectory. To enhance the energy concentration of Eq. (5), the 2D GD estimation is as follows:

Substituting Eq. (5) into Eq. (6), we can obtain:

Next, we perform a 1D integration of A along the time direction to compress the ambiguous time-frequency energy into the GD trajectory. This process can be expressed as Eq. (8):

Combining Eq. (7) and Eq. (8), we can obtain:

Eq. (9) illustrates that for weakly frequency-varying signals as described by Eq. (4), the TSST is capable of producing an optimal time-frequency representation. This is achieved by compressing the ambiguous time-frequency energy onto the group delay (GD) trajectory. Nonetheless, in practical scenarios, mechanical failure-induced vibration signals are frequently tainted with noise and exhibit a high degree of complexity. To augment the energy concentration within the time-frequency representation (TFR) for signals that are both strongly frequency-varying and strongly time-varying, the subsequent section will introduce the technique of time-reassigned multi-synchro squeezing transform. This method is designed to enhance the clarity and precision of the TFR, thereby facilitating more accurate analysis and diagnosis of mechanical faults.

2.2. Time-reassigned multi-synchro squeezing transform

For a strongly frequency-varying signal, where $\exists \epsilon$ is small enough and $\forall \omega$ satisfies conditions $\left|A\text{'}\left(\omega \right)\right|\le \epsilon$ and $\left|\phi \text{'}\text{'}\left(\omega \right)\right|\le \epsilon$, the signal given by Eq. (1) can be extended as Eq. (10):

The Fourier transform of the Gaussian window function used in STFT can be expressed as Eq. (11):

Substituting Eq. (10) into Eq. (3), we obtain Eq. (12):

According to Eq. (6), we can obtain the 2D GD estimation as Eq. (13):

According to Eq. (13), for signals with strong frequency variations, the expression given by Eq. (6) cannot provide an accurate estimation of the true GD of the signal. Now, substituting A into Eq. (13), we obtain Eq. (14):

Eq. (14) indicates that the group delay $-\phi \text{'}\left(\omega \right)$ is a fixed point of $\widehat{t}(t,\omega )$, implying that a fixed-point iteration algorithm can be employed to reduce the error between C and D. The first iteration can be expressed as Eq. (15):

As can be seen from Eq. (15), the fixed-point iteration algorithm effectively constructs a new 2D GD estimation $\widehat{t}\left(\widehat{t}\right(t,\omega ),\omega )$. Then, we can derive (16):

Eq. (16) implies that after one iteration, the new 2D GD estimation $\widehat{t}\left(\widehat{t}\right(t,\omega ),\omega )$ is already closer to $-\phi \text{'}\left(\omega \right)$ than $\widehat{t}(t,\omega )$. By performing a second iteration, we can further obtain Eq. (17):

From Eq. (17), we can obtain Eq. (18):

Comparing Eq. (18) with Eq. (16), the results indicate that with each iteration, the newly constructed 2D GD estimation becomes closer to the true $-\phi \text{'}\left(\omega \right)$. Denoting ${\widehat{t}}^{\left[N\right]}\left(t,\omega \right)$ as the newly constructed 2D GD estimation after the $N$th iteration, we obtain Eq. (19):

Eq. (19) indicates that when the number of iterations is sufficiently large, ${\widehat{t}}^{\left[N\right]}\left(t,\omega \right)$ will approach $-\phi \text{'}\left(\omega \right)$ indefinitely, i.e., as show in Eq. (20):

Replacing ${\widehat{t}}^{\left[N\right]}\left(t,\omega \right)$ with $\widehat{t}(t,\omega )$ in Eq. (8), we obtain:

After sufficient iterations, we can obtain Eq. (22):

Eq. (22) demonstrates that after sufficient iterations, the time-frequency energy of Eq. (21) can be effectively compressed onto the GD trajectory, even for signals with strong frequency variations.

3.1. Convolutional Layer

The CL executes a sliding convolution operation on the input data using its set of kernels, adhering to a predefined stride. This process effectively captures features from localized regions of the input. The output of the convolution is subsequently subjected to an activation function, yielding the resultant feature maps. In contemporary practice, the ReLU has emerged as the activation function of choice, favored for its merits such as minimal computational overhead and accelerated training kinetics. To encapsulate the essence of the convolutional layer's mathematical framework, its model is articulated in Eq. (23):

where, * denotes the convolution operation; $M_j$ represents the selected input mapping; $l$ is the $l$th layer in the network; $k$ is the kernel matrix with a size of $S$×$S$; and $f$ is the nonlinear activation function.

3.2. Subsampling layer

After each convolutional layer, a single subsampling layer is applied. The purpose of this layer is to reduce the size of the input features and the number of network parameters. The mathematical model can be described as Eq. (24):

where, down(·) represents the subsampling function. Typically, this function sums up each distinct $n$×$n$ block in the input image, resulting in an output image that is smaller by a factor of $n$ in both spatial dimensions. Each output mapping has its own multiplicative bias $\beta$ and additive bias $b$. The subsampling function chosen in this paper is max pooling. Its main principle is to divide the input image into a set of non-overlapping rectangles, and for each such subregion, the maximum value is output.

3.3. Subsampling layer

The fully connected layer is a traditional feedforward neural network where all neurons are connected to all activations of the previous layer. Its purpose is to collect and classify all features. The output layer uses the Softmax function as the activation function. The Softmax function takes an arbitrary real-valued vector and compresses it to values between 0 and 1. The Softmax function is defined as follows Eq. (25):

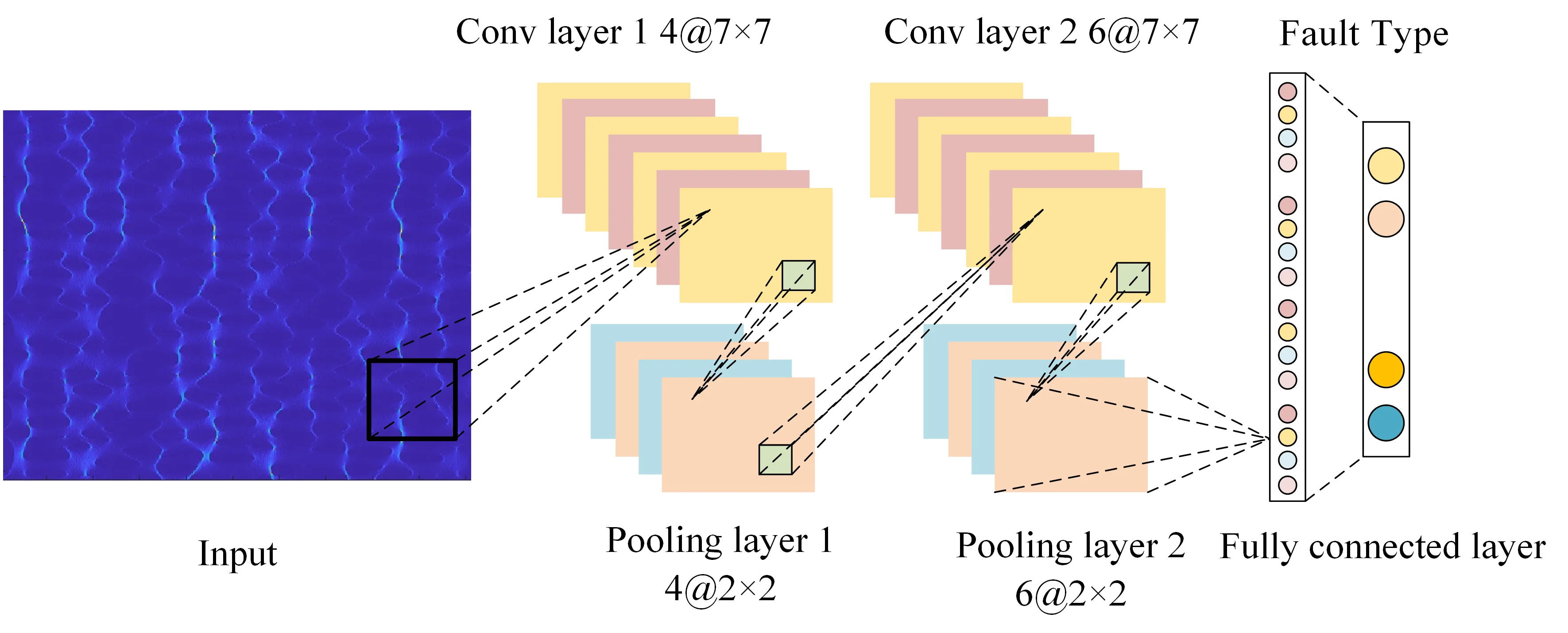
The ADAM optimization algorithm is employed to train the CNN, thereby optimizing the network parameters, specifically the weights and biases. ADAM's prowess lies in its ability to dynamically adjust the learning rate for each parameter by leveraging the first-order moment estimate (mean) and the second-order moment estimate (variance) of the gradient. This adaptive approach has been instrumental in enhancing the optimization process of CNN. Within the scope of this study, ADAM is utilized as both the feature extractor and classifier for the diagnosis of rolling bearing faults. To mitigate the risk of model overfitting, dropout operations are strategically incorporated into the FCL. The detailed architecture of the network is delineated in Table 1 and illustrated in Fig. 1.

Fig. 1The Structure of CNN

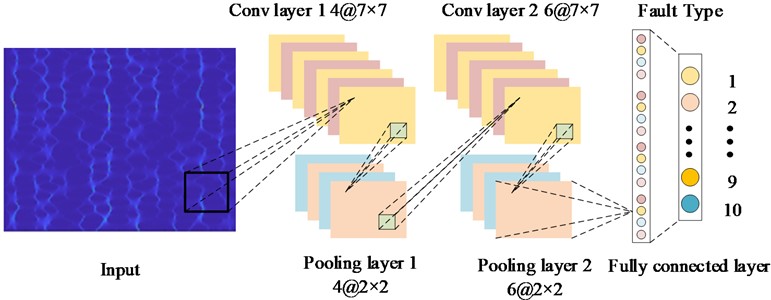
In Fig. 1, the input is a two-dimensional image. Firstly, four layers of convolution operations are performed to extract the features of the frequency domain image of the fault vibration signal. Then, the dimension is reduced through the pooling layer. After undergoing the above-mentioned convolution and pooling processes, all features are combined through the fully connected layer, and softmax is used to classify different features, thereby obtaining different bearing fault categories.

3.4. Reverse parameter update

For a specific classification task, the training objective of a CNN is to minimize the loss function of the network, thus it is crucial to select an appropriate loss function. Common loss functions include mean squared error, cross-entropy, and negative log-likelihood. In this paper, we choose the cross-entropy loss function, which has proven to be effective, and its expression is as follows Eq. (26):

where, $n$ represents the number of samples for a specific fault category; $t$ is the predicted value; and $y$ is the true value. During the training process, the method used to minimize the loss function is gradient descent. By taking the first-order partial derivative of Eq. (26), the learnable parameters ($w$ and $b$) of the CNN can be updated layer by layer, as show in Eq. (27) and Eq. (28):

where, $w\mathrm{\text{'}}$ and $b\mathrm{\text{'}}$ represent the updated weights and biases, respectively; $w$ and $b$ are the current weights and biases; $\eta$ is the learning rate parameter, which controls the step size of weight updates. If $\eta$ is too large, it can cause the network to converge to a local optimum; if $\eta$ is too small, it will increase the training time of the network.

3.5. Reverse parameter update

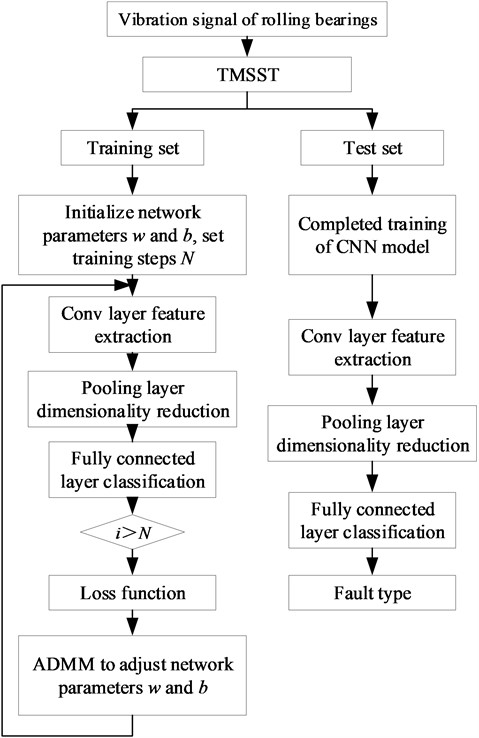
The fault diagnosis method based on CNN can integrate signal preprocessing, fault feature extraction, and fault pattern classification to achieve the specific process of adaptive extraction of fault features and intelligent diagnosis, as shown in Fig. 2. The collected vibration signals are divided into training and testing sets after TMSST. Firstly, the training set is input into the CNN for parameter learning, and the weights ($w$) and biases ($b$) are continuously updated using the gradient descent method. Then, the trained parameters are applied to the testing set to obtain the fault diagnosis results.

4.1. Dataset description

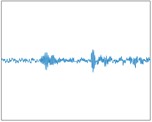
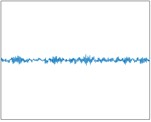
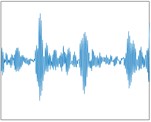
Fig. 3 shows the experimental platform, The testbed comprises a motor, torque sensor, power meter, and electronic controller. The bearing vibration signals are measured by sensors, and the amplitudes of these signals are represented by acceleration (https://engineering.case.edu/bearingdatacenter/apparatus-and-procedures).

To evaluate the performance of the proposed method, real bearing data were employed, which originated from the Bearing Fault Database of Case Western Reserve University [25]. This bearing fault database is a widely used resource that contains bearing vibration data under different operating conditions and fault modes, and is extensively employed in research on fault diagnosis and prediction. The testbed comprises a motor, torque sensor, power meter, and electronic controller. The bearing vibration signals are measured by sensors, and the amplitudes of these signals are represented by acceleration. The database includes both normal data and data from various fault modes, such as inner race faults, outer race faults, and rolling element faults. Each fault mode has multiple samples under different operating conditions, including varying parameters like rotational speed, load, and operating time. SKF's 6205-2RS deep groove ball bearing was taken as an example, and the drive-end bearing data were selected for verification. Single-point faults were arranged on the inner ring, outer ring, and rolling elements of the rolling bearing using electrical discharge machining techniques. Three fault diameters of 0.18, 0.36, and 0.54 mm were considered, with all faults having a depth of 0.28 mm. In total, nine fault types were examined. In this experiment, the length of each segment was determined to be 300 samples. 400 samples were constructed for each type of signal feature, and One-hot encoding was adopted to label ten different bearing operating conditions. The dataset was then divided into a training set and a test set in a 7:3 ratio. The construction of rolling bearing samples is summarized in Table 2. It includes ten different operating conditions, including normal state and nine different fault states, and the same proportion of data sets is taken.

Fig. 3Fault bearing vibration signal acquisition platform

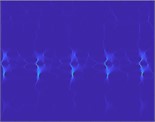
Fig. 4TMSST time-frequency diagrams for different types of faults: a) Normal; b) 0.17 mm rolling fault; c) 0.17 mm inner fault; d) 0.17 mm outer fault; e) 0.36 mm rolling fault; f) 0.36 mm inner fault; g) 0.36 mm outer fault; h) 0.54 mm rolling fault; i) 0.54 mm inner fault; j) 0.54 mm outer fault

a) Normal

b) Fault 1

c) Fault 2

d) Fault 3

e) Fault 4

f) Fault 5

g) Fault 6

h) Fault 7

i) Fault 8

j) Fault 9

Traditional time-domain analysis has difficulties in accurately representing the damage severity and fault type characteristics of rolling bearings. Therefore, by leveraging the uniqueness of TMSST encoding in mapping time series, the original vibration signals are encoded to generate distinct fault patterns, as shown in Fig. 4. Subsequently, these patterns are classified using CNN for the identification of 10 types of rolling bearing features.

Fig. 4 presents the TMMST diagrams for ten distinct fault types. It is evident that traditional time-domain analysis of fault signals struggles to precisely articulate the extent of deterioration and the distinctive characteristics of various fault types in rolling bearings. Consequently, employing the time reassignment multi-synchronous compression transformation to convert the time-domain signals of rolling bearings into 2D time-frequency images can significantly amplify the discernible features of different fault types. As depicted in Fig. 4, signals characterized by dissimilar damage features and fault types are challenging to discern in the time domain, whereas 2D images are adept at effectively extracting their fault characteristics. Furthermore, this study conducts a comparative analysis of TMMST with several other signal processing techniques, including the STFT, HHT, WVD, Synchronous Compression Transform (SCT), Multiscale Synchronous Compression Transform (MS-SCT), Time-Reassigned Multisynchronous Compression Transform (TR-MS-SCT), and Time-Reassigned Synchronous Compression Transform (TR-SCT). For instance, in fault type 2, the corresponding 2D image is displayed in Fig. 5. Post these transformations, the CNN is integrated to classify the feature maps corresponding to the 10 types of faults.

Fig. 5Result chart of frequency domain variation methods for 0.17 mm inner fault at different times

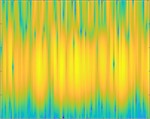
a) STFT

b) HHT

c) WVD

d) SST

e) MSST

4.2. Experimental result

To further verify the reliability of the proposed method, TMSST-CNN was used to identify ten types of faults in rolling bearings. There are a total of 4000 samples in the training and testing sets, divided into ten types of faults. In this section, the dataset was shuffled and the fault diagnosis model of TMMST-CNN was used to verify the model with different proportions of training and testing sets. The verification results are shown in Fig. 6.

From the confusion matrices presented in Figs. 5-6, it is evident that when the proportion of the training set is set to 70 %, a higher accuracy is achieved compared to when it is set to 60 %. Additionally, it can be effectively observed that the majority of misclassifications occur primarily in the categorization of Fault 6 and Fault 9. Examination of Fig. 4 reveals that the faults prone to misclassification exhibit insufficiently distinct characteristics in terms of energy distribution and varying fluctuation durations. However, upon undergoing the TMSST transformation, these differences become more prominent, resulting in a richer set of characteristics. To further validate the superiority of the method proposed in this study, a comparison was conducted between TMMST and other methods.

4.3. Experimental comparison

To verify the superiority of the proposed method, in this section, TMMST was compared with Short Time Fourier Transform, Hilbert Huang Transform, Wigner Ville Distribution, Synchronous Compression Transform, and Multiscale Synchronous Compression Transform. To highlight the superiority of TMSST-CNN, the accuracy, precision, and recall in the confusion matrix were used as evaluation indicators. Accuracy is the overall evaluation of the identification effect of all types of load appliances in the test set. The values of these evaluative metrics are bounded within the interval [0,1], where a higher value indicates superior identification capabilities of the algorithmic model [21]. These metrics are computed using the formulas presented in Eq. (29-32):

Fig. 6Performance of the method proposed in this article on different training sets: a) the accuracy of each type of fault when the training set is 60 %, b) the accuracy of each type of fault when the training set is 70 %

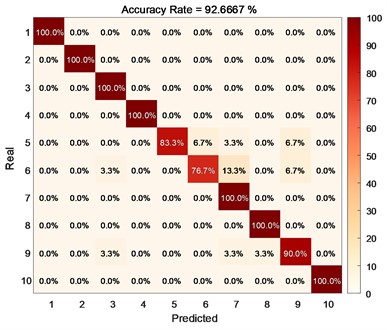
a)

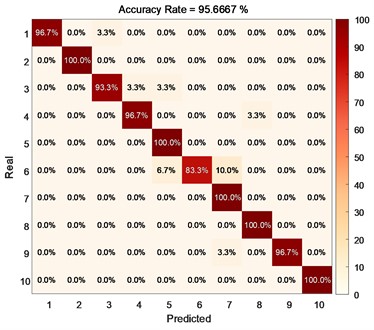
b)

In Table 3, $R_{Acc}$ represents the proportion of correctly predicted samples out of the total number of samples. In fault diagnosis, a high relative accuracy indicates that the model is able to reliably identify faulty and non-faulty states. $R_{Pre}$ is the proportion of actual positive samples (faulty state) among the predicted positive samples, reflecting the model’s ability to avoid misdiagnosing non-faulty states as faulty. $R_{Rec}$, also known as recall, signifies the model's capability to capture the majority of faulty states, thereby reducing the risk of missed detections. The $F_{1-score}$, on the other hand, provides a balanced consideration of both precision and recall, making it highly useful for evaluating the overall performance of the model in specific applications.

In the formula, $G$ represents the number of correctly classified fault types in the test set; $N$ represents the total number of fault types in the test set; $T_P$ is a true positive, representing the number of faults in this article where the predicted label of the fault type in the test set matches the true label; $F_N$ is a false negative, which represents the number of faults in the test set that were mistakenly identified as other types of faults for a certain type of fault; $F_P$ is false positive. In this article, it represents the number of faults in the test set that were incorrectly identified as a certain type of fault, while other types of faults were identified as such.

Through the analysis of Table 3, it can be seen that compared to directly using time-domain signals for evaluation in CNN models, time-frequency transformation can effectively improve the diagnostic rate of fault types. Meanwhile, compared to traditional time-frequency transformation methods, the method proposed in this paper has better performance. $R_{Acc}$, $R_{Pre}$, $R_{Rec}$, and $F$ all have the best performance, with a global accuracy of 95.67 %. They have very high accuracy for 10 types of faults in rolling bearings and have a certain degree of robustness. Therefore, TMSST's processing of time-domain signals can effectively enhance data features, and TMSST-CNN is a method with a good diagnostic success rate for bearings.