A convolutional neural network method based on Adam optimizer with power-exponential learning rate for bearing fault diagnosis

Wang, Youming; Xiao, Zhao; Cao, Gongqing

doi:10.21595/jve.2022.22271

Journal of Vibroengineering

Browse Journal

Submit article

Published: 30 June 2022

Check for updates

A convolutional neural network method based on Adam optimizer with power-exponential learning rate for bearing fault diagnosis

Youming Wang¹

Zhao Xiao²

Gongqing Cao³

¹Xi’an Key Laboratory of Advanced Control and Intelligent Process (ACIP), Xi’an, 710121, China

^{1, 2, 3}School of Automation, Xi’an University of Posts and Telecommunications, Xi’an, 710121, China

Corresponding Author:

Youming Wang

Cite the article Download PDF

Downloads 1190

WoS Core Citations 26

CrossRef Citations 31

Abstract

The extraction of early fault features from time-series data is very crucial for convolutional neural networks (CNNs) in bearing fault diagnosis. To address this problem, a CNN framework based on identity mapping and Adam optimizer is presented for learning temporal dependencies and extracting fault features. The introduction of four identity mappings allows the deep layers to directly learn the data from the shallow layers, which alleviates the gradient disappearance problem caused by the increase of network depth. A new Adam optimizer with power-exponential learning rate is proposed to control the iteration direction and step size of CNN method, which solves the problems of local minima, overshoot or oscillation caused by the fixed values of the learning rates during the updating of network parameters. Compared to existed methods, the identification accuracy of the proposed method outperformed that of other methods for bearing fault diagnosis.

A convolutional neural network method based on Adam optimizer with power-exponential learning rate for bearing fault diagnosis

Highlights

Proposed a new CNN model to solve the problem of rolling bearing fault diagnosis.
By embedding identity mapping, the problem of degradation and gradient disappearance caused by increasing depth of neural network model is solved.
The proposed Adam optimizer implements adaptive changes to the learning rate of the optimizer by adding a power-exponential correction factor.
Experimental results show that the proposed method can diagnose the fault type of bearing fault data more accurately.

1. Introduction

Rotating machinery has become one of the key components of the overall system of mechanical equipment. Rolling bearing is the basic component in rotating machinery. Early fault diagnosis, fault prediction and timely maintenance become an effective means to ensure the safety and reliability of rotating machinery. Since the rich fault information in vibration signal can reflect the real state of the fault, the vibration-based fault detection method has been applied to early fault diagnosis of bearing. Previously, machine learning and statistical inference technology has been applied to fault signal analysis, such as artificial neural network (ANN) [1], random forest (RF) [2], support vector machine (SVM) [3], fuzzy inference [4, 5], Fuzzy-Neuro network [6] and Gaussian process regression (GPR) [7]. Pankaj et al. [8] used a neuro-fuzzy hybrid approach to identify transverse cracks in fiber-reinforced composite beams. Koteleva et al. [9] used a classifier based on artificial neural network and Park vector method to predict motor bearing wear. Harutyunyan et al. [10] developed a fault detection method based on multi-level model by using the hierarchical structure of detection and diagnosis methods. Li et al. [11] proposed a new fault diagnosis model which combined binarized deep neural network with improved random forests for real-time fault diagnosis. Lu et al. [12] presented an innovative diagnosis model using the complementary ensemble empirical mode decomposition with kernel support vector machines to evaluate the health condition of bearings in terms of defect severity. Nikitin et al. [13] developed a model of a fault diagnosis system for electromechanical objects in a robotic workplace by combining an electromechanical module based on a fuzzy inference system and a CNC (Computer Numerical Control) based machine diagnosis example. Kumar et al. [14] used a Gaussian Process Regression (GPR) approach to model prediction of rolling bearing failure and degradation trends. Neural network is an effective data-driven feature extraction method for fault identification and feature extraction. The steps of fault diagnosis method based on neural network is as follows: firstly, the sample signal is preprocessed. Secondly, the appropriate network is selected and the network training is performed on the sample signal. Finally, a suitable network model which can automatically complete feature extraction is obtained by updating and iterating of network parameters. In recent years, deep learning has many advantages and potential for processing non-linear and non-stationary time series data for feature extraction and pattern classification [15-17]. Some typical deep learning methods have been reported, such as the deep belief network (DBN) [18], the recurrent neural network (RNN) [19] and the convolutional neural network (CNN) [20]. DBN is a probability generation model, which uses layer by layer greedy learning algorithm to optimize the connection weight of deep neural network. The parameter sharing mechanism of RNN has the ability of translation invariant generalization and pattern memory of patterns in sequence data. Mandal et al. [21] proposed an online fault detection and classification method based on DBN. Veerasamy et al. [22] presented the detection of high impedance fault in photovoltaic integrated power system using recurrent neural network-based LSTM approach.

CNN has the ability of adaptive feature extraction [23], which eliminates the influence of expert experience on the feature extraction process. CNN is a feedforward neural network. The input signal data can be input into the network without vectorization. The local weight sharing of CNN reduces the complexity of the network and avoids the complexity of data reconstruction in the process of feature extraction and classification. CNN has great potential in mechanical health recognition. Grezmak et al. [24] took the vibration signal as the time series data, which converted it into a spectrum image through wavelet transform, classified it with CNN finally. Mukherjee et al. [25] proposed a light-weight CNN which utilizes vibration sensor measurements for fault event estimation of machines. Kumar et al. [26] adopted a CNN model which combined adaptive gradient optimizer and BN to optimize the performance of fault diagnosis. Lomov et al. [27] proposed a novel temporal CNN1D2D architecture for various recurrent and convolutional structures for process fault detection. Zhu et al. [28] proposed an intelligent fault diagnosis algorithm based on CNN, which converts the original signal into two-dimensional image and extracts fault features through CNN. Liu et al. [29] proposed a fault diagnosis method based on LeNet-5, which realized accurate and stable fault diagnosis of rotating machinery under noise environment and variable load conditions. Although CNN has achieved success in fault diagnosis in the past few years, the fault classification problem of highly complex nonlinear signals with deep network structures is still difficult to solve [30]. Since the parameter update of traditional CNN relies on the back-propagation of multi-layer gradients, the increase of CNN depth causes the problem of degradation and gradient disappearance, which leads to overfitting of training data and degradation of recognition accuracy. To solve the problem, the identity mapping is proposed between the layers [31], where the deep layers are copied from the learned shallow layers without adding additional parameters and increasing the computational complexity [31, 32]. When identity mapping is embedded between layers, the training accuracy and speed can be improved.

When the CNN is used to train and classify the fault bearing data, it is crucial to obtain an optimized deep learning model by adjusting weight parameters of each layer. CNN uses the optimizer to calculate and update various network parameters to gradually approach and reach the optimal value, so as to minimize or maximize the loss function and improve the iterative efficiency.

Common optimizers include stochastic gradient descent (SGD) algorithms, adaptive gradient (AdaGrad) algorithms, root mean square prop (RMSProp) algorithms and adaptive moment estimation (Adam) algorithms, etc. The optimizer defines the magnitude and speed of each parameter update by setting the learning rate [33]. The learning rate guides how the weights of the network are adjusted by the gradient of the loss function. If the learning rate is set too large initially, although the learning speed is fast, the training value swings back and forth around the optimal value, which is prone to oscillation. Each iteration may have overshoot, which will continue to diverge on both sides of the extreme point. If the learning rate is setting too small, the convergence speed is slow and over fitting may occur. Although practical optimization methods for deep neural networks are based on SGD, some unexpected problems may occur in hyperparameter adjustment such as local optimal solution and slow convergence [34]. Adagrad [35] can adaptively adjust the learning rate. However, the continuous accumulation of gradient square will reduce the learning rate to too small to update effectively. RMSProp [36] algorithm combined with the exponential moving average of the square of the gradient to adjust the change of the learning rate. Adam optimizer [37-39] combines the advantages of AdaGrad and RMSProp optimization algorithms, which dynamically adjusts the exponential decay rate for the 1st moment estimates and the 2nd moment estimates to update parameters. Adam algorithm is suited for a mass of data and non-stationary objective optimization with noisy and sparse gradients. Deep neural networks often contain a large number of parameters. Most of the loss functions in deep learning are convex functions [40], which makes it easy to obtain the global optimal solution. However, multiple local minima in the model training resulting in weak convergence when the loss function is non-convex for Adam optimization of deep learning model.

In this paper, a novel CNN model with 8 convolution layers based on identity mapping and Adam optimizer is proposed for rolling bearing fault diagnosis. By embedding identity mapping, the problem of degradation and gradient disappearance caused by the increase of the depth of neural network model is solved. According to the characteristics of exponential function, the increase of iterative step size will reduce the learning rate, so as to ensure the stability of the model in the later stage of training. It is found that the convergence trend of the model is close to the change of power-exponential function. In the proposed method, the iteration direction and step size of traditional Adam is evaluated by the power-exponential learning rate, where the learning rate of deep learning model can be adjusted adaptively by that of the previous stage, so as to improve the convergence performance of the network model.

The rest of this paper is organized as follows. Section 2 introduces some theoretical background, including the Adam optimizer and identity mapping. The overall implementation of proposed CNN is illustrated in detail. Adam optimizer with power-exponential learning rate is further proposed. In Section 3, the MaFaulDa bearing dataset and the Case Western Reserve University (CWRU) bearing dataset are used to compare and verify the performance of the proposed network, traditional general network and traditional method. The main conclusions of this paper are summarized in Section 4.

2. Convolutional neural network model based fault diagnosis

2.1. Adam optimizer with power-exponential learning rate

To accelerate the optimization process of traditional Adam optimizer in CNN model, an Adam optimizer with power-exponential learning rate is used to train CNN model, where the iteration direction and step size are controlled by the power-exponential learning rate to reach the optima. The power-exponential learning rate can be adjusted adaptively according to the learning rate of the previous stage and the gradient relationship between the previous stage and the current stage. The previous gradient value is used to adjust the correction factor to meet the requirements of adaptive adjustment. This helps to adjust the learning rate in a small range, the parameters of each iteration are relatively stable, the learning step is selected according to the appropriate gradient value to change the convergence performance of the network model and ensure the stability and effectiveness of the network model.

Adam optimizer is an algorithm that performs a stepwise optimization on a random objective function [41]. The gradient update rules for the parameters are:

1

θ_{t + 1} = θ_{t} - \frac{η}{\sqrt{{\hat{v}}_{t} + ε}} {\hat{m}}_{t},

2

m_{t} = β_{1} m_{t - 1} + (1 - β_{1}) g_{t},

3

v_{t =} β_{2} v_{t - 1} + (1 - β_{2}) g_{t}^{2},

where $θ_{t}$ , $θ_{t + 1}$ is objective function, $t$ is time parameter, $β_{1}$ , $β_{2} \in [0,1)$ represents the decay rate of the moving mean index, $η$ is learning rate, $ε$ is a constant parameter, $ε =$ 0.9999, ${\hat{m}}_{t}$ and ${\hat{v}}_{t}$ is the first-order and second-order moment estimation after the gradient modification respectively. If $m_{t}$ and $v_{t}$ are initialized to zero vector, they will be offset to zero. It is necessary to correct the deviation [42], ${\hat{m}}_{t}$ and ${\hat{v}}_{t}$ will be corrected as:

4

{\hat{m}}_{t} = \frac{m_{t}}{1 - β_{1}^{t}}, {\hat{v}}_{t} = \frac{v_{t}}{1 - β_{2}^{t}} .

In the original Adam optimizer algorithm, the first-order moment to non central second-order moment estimation is modified, and the offset is reduced. However, in the process of rolling bearing fault diagnosis and classification, the algorithm has poor effect in fitting the convergence state of the model. A correction factor was added to the learning rate to address the shortcomings of the original Adam optimizer algorithm. The power-exponential learning rate of the downward trend is used as the basis, and the gradient value of the previous stage is used to adjust it to meet the requirements of adaptive adjustment, so as to change the convergence performance of the network model. The model for power-exponential learning rate is:

5

η = η_{0} m^{- k},

where $η_{0}$ is initial learning rate, $η_{0} = 0.1$ , $k$ is a hyperparameter, $k = 0.8$ , $m$ is the iterative intermediate, $m$ is determined by the number of iterations and the maximum number of iterations is defined as follows:

6

m = 1 + \frac{t}{R},

where $t$ is iteration number, $R$ is the maximum number of iterations. When Eq. (6) is combined with Eq. (5), the form of learning rate update is:

7

η (t) = η_{0} {[1 + \frac{t}{R}]}^{- k} .

The pseudo code of the improved Adam optimization algorithm is shown in Table 1.

Table 1Improved Adam optimization algorithm

Algorithm: Adam with power-exponential learning rate

Require:

η_{0} = 0.1

,

β_{1} = 0.9

,

β_{2} = 0.999

,

ε = 0.9999

,

q = 0.8

Require: Initialize time step

t

, parameter

θ_{t}

, first/second moment estimation

{\hat{m}}_{t}

,

{\hat{v}}_{t}

while stopping criterion is not met do

Update first/second moment

m_{t} \leftarrow β_{1} m_{t - 1} + (1 - β_{1}) g_{t}

,

v_{t} \leftarrow β_{2} v_{t - 1} + (1 - β_{2}) g_{t}^{2}

Moment correction:

{\hat{m}}_{t} \leftarrow m_{t} / 1 - β_{1}^{t}

,

{\hat{v}}_{t} \leftarrow v_{t} / 1 - β_{2}^{t}

Power-exponential learning rate

η \leftarrow η_{0} m^{- k}

,

m \leftarrow 1 + \frac{t}{R}

η (t) \leftarrow η_{0} {[1 + \frac{t}{R}]}^{- k}

Update parameters:

θ_{t} \leftarrow θ_{t - 1} - η_{0} {[1 + \frac{t}{R}]}^{- k} \frac{{\hat{m}}_{t}}{\sqrt{{\hat{v}}_{t}} + ε}

end while

Return optimized parameters

θ_{t}

2.2. Convolutional neural network with improved Adam algorithm and identity mapping

To solve the problems of degradation and gradient disappearance of traditional CNN, the identity mapping is embedded between the layers [31]. As shown in Fig. 1, the module is composed of several convolution layers and a shortcut connection channel. Identity mapping $x$ is added through shortcut connection channel. ReLU is used as the activation function to alleviate the problem of gradient disappearance caused by network deepening. Shortcut connection channel is the difference between identity mapping and ordinary CNN, which enables the data calculated from the shallow convolution layer to reach the deep convolution layer directly. This module alleviates the vanishing gradient problem caused by increasing the number of convolutional layers and improves the training accuracy of multi-convolutional layer CNNs.

Fig. 1Identity mapping module

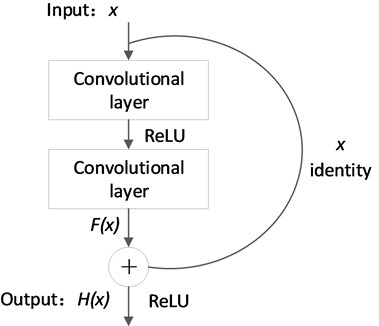
The output of $H (x)$ is converted to $F (x) + x$ , that is:

8

H (x) = F (x) + x,

where $x$ is the input, $H (x)$ is the desired output of the underlying mapping, $F (x)$ is the residual mapping. The optimal learning of the network aims to make $F (x)$ tend to 0. Arbitrary L-layer features of deep neural network can be obtained by recursion:

9

H (x_{L}) = \sum_{i = 1}^{L - 1} F (x_{i}) + x_{L},

where $H (x_{L})$ is the output of the $l$ th layer. Eq. (9) is substituted in back propagation:

10

\frac{\partial L o s s}{\partial x_{L}} = \frac{\partial L o s s}{\partial x_{L}} (1 + \frac{\partial}{\partial x_{L}} \sum_{i = 1}^{L - 1} F (x_{i})) .

It should be noted from Eq. (10) that the problem of gradient vanishing will not occur even if the weight of the intermediate layer matrix is small.

The CNN model based on identity mapping built in this paper is shown in Fig. 2. The model consists of 10 convolution layers, 1 maximum pooling layer and 1 full connection layer. After the full connection layer, the improved Adam optimizer is used to update and calculate the network parameters which affect the model training and output to make them approximate or reach the optimal value. Finally, the data is passed through the softmax classifier and the corresponding classification results are output.

Fig. 2Structure of CNN model based on identity mapping

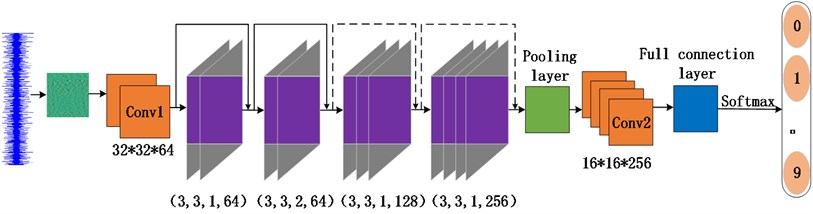
Eight convolution layers with identity mapping are embedded in the network. In the involved convolution layer, different step lengths and output channels are used. The size of the convolution kernel is all 3×3. In the fourth convolution layer, the step length is 2, the size of the convolution kernel remains unchanged, which can reduce the translation times of the convolution kernel and the amount of calculation in the network model. The structural parameter of convolution layers with identity mapping is shown in Table 2. In addition, BN layer can not only reduce the number of training steps and accelerate the convergence on the premise of reaching the same accuracy, but also reduce the disappearance of gradient and improve the generalization ability. When the input and output of the shortcut connection have different numbers of channels, zero filling is used to match the number of channels. In order to extract significant bearing fault features and improve the network training efficiency, the maximum pool is selected. The pooled window size is 2×2.

Table 2Structural parameters of eight convolution layers with identity mapping

Identity mapping convolution layer	Convolution layer parameters
Conv1_1	Conv(3,3,1,64)
Conv1_2	Conv(3,3,1,64)
Conv2_1	Conv(3,3,1,64)
Conv2_2	Conv(3,3,2,64)
Conv3_1	Conv(3,3,1,128)
Conv3_2	Conv(3,3,1,128)
Conv4_1	Conv(3,3,1,256)
Conv4_2	Conv(3,3,1,256)

3. Experimental results

3.1. Data acquisition

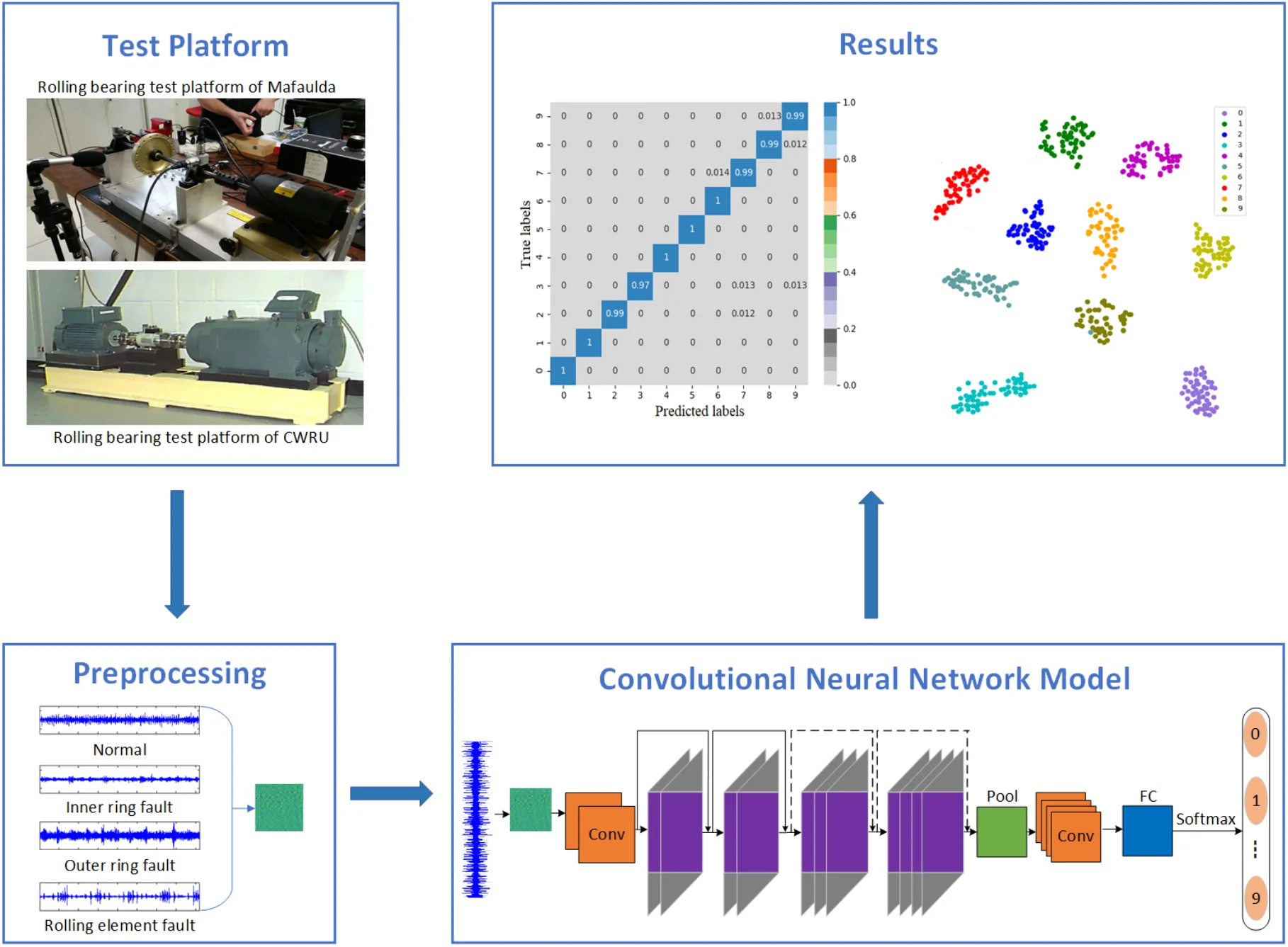
The datasets of the experiments conducted in MaFaulDa [43] and Case Western Reserve University (CWRU) [44] are used to verify the effectiveness of the proposed method. MaFaulDa bearing test bench is monitored by two different sets of equipment, including three industrial sensors, 601A01 accelerometer, a tachometer and a microphone. Three defective bearings, including outer ring failure, inner ring failure, and rolling element failure were used in the experiments. The experiment parameters of MaFaulDa bearing monitoring are shown in Table 3. The rolling bearing test platform of CWRU is shown in Fig. 3. An acceleration sensor with a frequency of 12 khz is used to collect CWRU bearing fault data at the driving end. The experimental platform includes three fault types of inner ring, outer ring and rolling element faults.

3.2. Data preprocessing

For MaFaulDa bearing dataset, 10 types of fault diagnosis signals are selected including no fault, the outer ring fault, inner ring fault, and rolling element fault under loads of 6 g, 20 g and 35 g. The fault categories are labeled 0-9. For the collected sample vibration signals, of which 80 % are used as the training set and 20 % as the test set. Each sample contains 1024 data points, which are transformed into 32×32 two-dimensional signals by time-frequency conversion of the original vibration signals.

Table 3MaFaulDa bearing fault diagnosis experiment parameters

Experimental specifications	parameter
Motor	1/4 CV DC
Frequency Range	700-3600 rpm
System weight	22 kg
Shaft diameter	16 mm
Shaft length	520 mm
Rotor	15.24 cm
Bearing span Number of balls Ball diameter	390 mm 8 0.7145 cm
Basic standard frequency	1.8710 CPM/rpm
Outer loop fault frequency	2.9980 CPM/rpm
Inner loop failure frequency	5.0020 CPM/rpm

Fig. 3Rolling bearing test platform of CWRU

For CWRU bearing dataset, the experimental platform contains three types of faults: inner ring, outer ring and rolling element faults. Each fault type includes three damage diameters of 0.18 mm, 0.36 mm and 0.53 mm. There are 10 fault types in total by adding normal state. There are 2000 samples for 10 fault types, the length of each data sample is 4096. The category is labeled 0-9. 1×4096 one-dimensional data is transformed into 64×64 two-dimensional characteristic matrix for processing, which is used as the input of CNN.

3.3. MaFaulDa bearing dataset fault diagnosis result analysis

In order to evaluate the performance of the CNN optimized by the improved Adam and identity mapping in MaFaulDa bearing dataset, the classification accuracies of different models are compared by 5-fold cross-validation. 5-fold cross-validation [45] is used to prevent over-fitting caused by complex models, which divides the original data into five groups, each subset data is used as a verification set, the other four groups of subset data are used as a training set, five models will be obtained. The five models are evaluated in the validation set respectively, and the average value of error is obtained as the final evaluation. 3 times of 5-fold cross-validation are carried out to calculate the mean value as the estimate of the accuracy of the algorithm. The compared models include the CNN with identity mapping, original network LeNet-5 and LSTM.

Table 4 shows the diagnosis results of the 5-fold cross-validation of the rolling bearing fault monitoring for different models. The LeNet-5 model contains 2 convolution layers and 2 pooling layers, 2 full connection layers and 1 output layer. On the MaFaulDa bearing fault dataset, the average classification accuracy of the LeNet-5 is 86.73 %, while the average classification accuracy of the traditional LSTM model is 77.52 %. Compared with the model LeNet-5, the CNN model as a deep network after embedding identity mapping has stronger recognition and diagnosis ability for MaFaulDa bearing dataset. The classification accuracy of the CNN method optimized by the improved Adam and identity mapping is improved by 3.05 % on the basis of the CNN method with identity mapping.

Table 45-fold cross-validation diagnosis results of rolling bearing fault monitoring with different models (%)

	Experiments times
Fault diagnosis model	1	2	3	4	5
Proposed method CNN with identity mapping One LeNet-5 LSTM	99.71	98.69	99.37	99.14	98.25
	96.44	95.31	96.25	95.94	96.07
	86.92	89.44	86.83	86.11	84.27
	76.92	79.65	82.63	80.81	74.36
Proposed method CNN with identity mapping Two LeNet-5 LSTM	97.68	99.87	98.34	98.36	98.70
	94.17	94.62	96.92	95.09	96.11
	86.92	89.44	86.83	86.11	84.27
	77.42	76.35	81.03	77.68	74.09
Proposed method CNN with identity mapping Three LeNet-5 LSTM	98.25	99.43	99.62	99.46	98.02
	96.39	95.28	96.37	95.90	96.15
	87.97	86.54	88.21	86.91	84.25
	79.85	80.31	76.55	73.19	72.06

The error matrix is an index to evaluate the classification accuracy of the algorithm. Each column of the error matrix represents the prediction category, the value of each column represents the accuracy of the data predicted for that category. Each row represents the real belonging category of the data, and the value of each row represents the accuracy of the data classification diagnosis of the category. In order to study the performance of the CNN optimized by the improved Adam, the TensorFlow framework is used to import the sklearn and seaborn function libraries under the combination of test targets and actual bearing combination fault classification, the error matrix is drawn by the heatmap. Set the heatmap visualization through the Cmap parameter to the greater the probability value, the darker the color. Fig. 4 shows the classification error matrix of 10 selected bearing fault diagnosis signals, including outer ring fault, inner ring fault and rolling element fault under normal operation state and 6 g, 20 g and 35 g load.

From Fig. 4(a) and (b), the average fault diagnosis recognition rate can reach 99.3 % and 94.5 % respectively by embedding the identity mapping. The method which using improved Adam optimizer has better diagnostic effect. From Fig. 4(c), LeNet-5 with two groups of convolution layers has poor diagnosis effect for outer ring fault under 6 g and 35 g loads and rolling element fault under 20 g load. The average diagnosis accuracy is 86.4 %, which is higher than 74 % of LSTM network. Compared with other models, on the one hand, the proposed model reduces the number of model parameters while extracting high-dimensional features after embedding identity mapping. On the other hand, Adam optimizer with power-exponential learning rate changes the convergence performance of the network, so that the model has stronger recognition and diagnosis ability for MaFaulDa bearing dataset.

3.4. CWRU bearing dataset fault diagnosis result analysis

To more intuitively illustrate the adaptive feature learning capability of the CNN optimized by the improved Adam and identity mapping, t-SNE algorithm [46] is used to visualize the effect characteristics of fault classification. t-SNE is a nonlinear dimensionality reduction algorithm for studying high-dimensional data, which maps high-dimensional data to two-dimensional or multi-dimensional suitable for observation. It constructs a probability distribution among high-dimensional objects, so that similar objects have a higher probability of being selected, and different objects have a lower probability of being selected. The test samples are input into the CNN trained by the improved Adam and identity mapping, the distribution of fault classification features is shown in Fig. 5.

Fig. 4Error matrix of fault diagnosis results

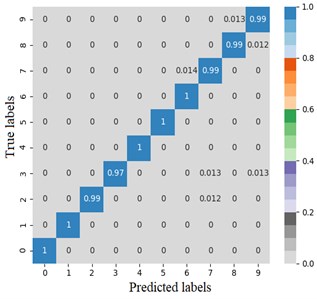
a) Proposed method

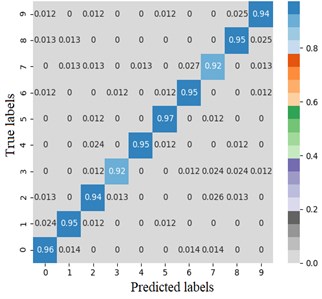
b) CNN with identity mapping

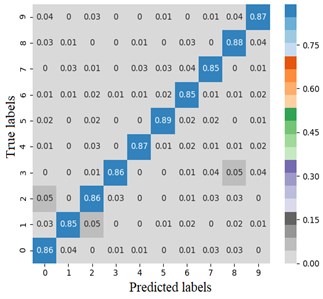
c) LeNet-5

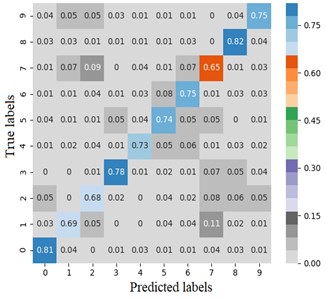
d) LSTM

Each color in Fig. 5 represents a fault type, including three different specifications of inner ring, outer ring, rolling element fault and normal state. The features learned by the model for each fault are highly separated. Deep learning is characterized by learning features through multiple layers of convolution, which can lead to a loss of detail. Therefore, classification accuracy can be improved by adding shortcut connection that combine local information from the first convolutional layer with global information from the final convolutional layer. The visualization result shows that the CNN optimized by the improved Adam and identity mapping can learn different fault features from bearing vibration data with good fault classification ability.

The common evaluation indexes of bearing fault diagnosis include F1 score, accuracy rate, precision rate and recall rate. The level of evaluation index directly affects the diagnostic ability and comprehensive performance of the model. In the case study of rolling bearing fault diagnosis, the same dataset is selected. The traditional SVM and BPNN methods [47], lenet-5 and LSTM methods use the same experimental environment as the proposed method, the experimental results are obtained by constructing the corresponding network structure. The experimental results of bearing fault monitoring and diagnosis are shown in Table 5. The diagnosis accuracy of CNN method optimized by the improved Adam and identity mapping is 98.53 %, which has higher diagnostic recognition rate. The average accuracy of SVM and BPNN are 83.77 % and 77.46 % respectively, both of which limit the data processing ability of the network and have poor fault diagnosis results. Traditional deep learning methods such as LeNet-5 suffer from the gradient vanishing problem. The identity mapping in our proposed method allows the deep layer to learn data directly from the shallow layer, which alleviates the gradient disappearance and overfitting problems associated with increasing network depth, extracts high-level abstract features and significantly improves the accuracy of bearing faults.

Fig. 5Distribution of fault classification features

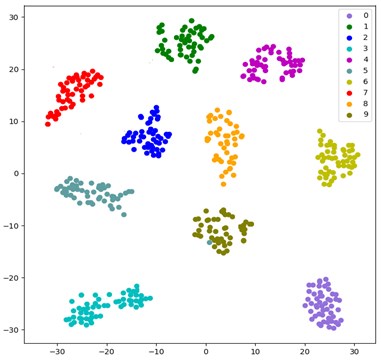
Table 5Fault monitoring and diagnosis results of rolling bearing with different models (%)

	Fault diagnosis model	Accuracy rate	Precision rate	Recall rate	F1 score
Deep learning method	Proposed method	98.53	98.38	98.02	98.19
	LeNet-5	94.41	93.26	93.14	93.19
	LSTM	95.55	94.61	94.95	94.77
Traditional method	SVM + EMD + Hilbert	83.77	–	–	–
Traditional method	BPNN + EMD + Hilbert	77.46	–	–	–

4. Conclusions

In this paper, a new CNN model with 8 convolution layers based on identity mapping and Adam optimizer is proposed to solve the problems of rolling bearing fault diagnosis. By embedding identity mapping, the data calculated from the shallow convolution layer can directly reach the deep convolution layer without adding additional parameters and increasing the computational complexity. The problem of degradation and gradient disappearance caused by increasing depth of neural network model is solved, and the training accuracy and speed of the CNN is improved. The proposed Adam optimizer implements adaptive changes to the learning rate of the optimizer by adding a power-exponential correction factor. The decay mechanism of the adaptive power-exponential learning rate guides the parameters to converge towards the global minima, which improves the convergence performance of the CNN network model. The performance of the proposed network, general network and traditional method are compared and verified by using MaFaulDa and CWRU bearing datasets. Compared with LeNet-5, LSTM and traditional SVM and BPNN fault diagnosis methods, the proposed method can diagnose the fault type of bearing fault data more accurately.

References

T. Tran, B.-S. Yang, F. Gu, and A. Ball, “Thermal image enhancement using bi-dimensional empirical mode decomposition in combination with relevance vector machine for rotating machinery fault diagnosis,” Mechanical Systems and Signal Processing, Vol. 38, No. 2, pp. 601–614, Jul. 2013, https://doi.org/10.1016/j.ymssp.2013.02.001

Publisher
B.-S. Yang, X. Di, and T. Han, “Random forests classifier for machine fault diagnosis,” Journal of Mechanical Science and Technology, Vol. 22, No. 9, pp. 1716–1725, Sep. 2008, https://doi.org/10.1007/s12206-008-0603-6

Publisher
R. Jegadeeshwaran and V. Sugumaran, “Fault diagnosis of automobile hydraulic brake system using statistical features and support vector machines,” Mechanical Systems and Signal Processing, Vol. 52-53, pp. 436–446, Feb. 2015, https://doi.org/10.1016/j.ymssp.2014.08.007

Publisher
Z. Li, H. Fang, and M. Huang, “Diversified learning for continuous hidden Markov models with application to fault diagnosis,” Expert Systems with Applications, Vol. 42, No. 23, pp. 9165–9173, Dec. 2015, https://doi.org/10.1016/j.eswa.2015.08.027

Publisher
A. Youssef, C. Delpha, and D. Diallo, “An optimal fault detection threshold for early detection using Kullback-Leibler Divergence for unknown distribution data,” Signal Processing, Vol. 120, pp. 266–279, Mar. 2016, https://doi.org/10.1016/j.sigpro.2015.09.008

Publisher
M. M. Gupta and D. H. Rao, “On the principles of fuzzy neural networks,” Fuzzy Sets and Systems, Vol. 61, No. 1, pp. 1–18, Jan. 1994, https://doi.org/10.1016/0165-0114(94)90279-8

Publisher
Y. Zhu, X. Cheng, and L. Wang, “A novel fault detection method for an integrated navigation system using Gaussian process regression,” Journal of Navigation, Vol. 69, No. 4, pp. 905–919, Jul. 2016, https://doi.org/10.1017/s0373463315001034

Publisher
P. C. Jena, “Fault assessment of FRC cracked beam by using neuro-fuzzy hybrid technique,” Materials Today: Proceedings, Vol. 5, No. 9, pp. 19216–19223, 2018, https://doi.org/10.1016/j.matpr.2018.06.277

Publisher
N. Koteleva, N. Korolev, Y. Zhukovskiy, and G. Baranov, “A soft sensor for measuring the wear of an induction motor bearing by the park’s vector components of current and voltage,” Sensors, Vol. 21, No. 23, p. 7900, Nov. 2021, https://doi.org/10.3390/s21237900

Publisher
G. Harutyunyan, S. Martirosyan, S. Shoukourian, and Y. Zorian, “Memory physical aware multi-level fault diagnosis flow,” IEEE Transactions on Emerging Topics in Computing, Vol. 8, No. 3, pp. 700–711, Jul. 2020, https://doi.org/10.1109/tetc.2018.2789818

Publisher
H. Li, G. Hu, J. Li, and M. Zhou, “Intelligent fault diagnosis for large-scale rotating machines using binarized deep neural networks and random forests,” IEEE Transactions on Automation Science and Engineering, Vol. 99, pp. 1–11, 2021, https://doi.org/10.1109/tase.2020.3048056

Publisher
Y. Lu, R. Xie, and S. Y. Liang, “CEEMD-assisted kernel support vector machines for bearing diagnosis,” The International Journal of Advanced Manufacturing Technology, Vol. 106, No. 7-8, pp. 3063–3070, Feb. 2020, https://doi.org/10.1007/s00170-019-04858-w

Publisher
Y. Nikitin, P. Božek, and J. Peterka, “Logical-linguistic model of diagnostics of electric drives with sensors support,” Sensors, Vol. 20, No. 16, p. 4429, Aug. 2020, https://doi.org/10.3390/s20164429

Publisher
P. S. Kumar, L. A. Kumaraswamidhas, and S. K. Laha, “Selection of efficient degradation features for rolling element bearing prognosis using Gaussian process regression method,” ISA Transactions, Vol. 112, pp. 386–401, Jun. 2021, https://doi.org/10.1016/j.isatra.2020.12.020

Publisher
B. Zhao, X. Zhang, Z. Zhan, and S. Pang, “Deep multi-scale convolutional transfer learning network: A novel method for intelligent fault diagnosis of rolling bearings under variable working conditions and domains,” Neurocomputing, Vol. 407, No. 24, pp. 24–38, Sep. 2020, https://doi.org/10.1016/j.neucom.2020.04.073

Publisher
Wei et al., “Rolling bearing fault diagnosis based on the deep neural networks,” (in Chinese), Modular Machine Tool and Automatic Manufacturing Technique, Vol. 11, pp. 88–91, 2017, https://doi.org/10.13462/j.cnki.mmtamt.2017.11.023

Publisher
F. Lv, C. Wen, M. Liu, and Z. Bao, “Weighted time series fault diagnosis based on a stacked sparse autoencoder,” Journal of Chemometrics, Vol. 31, No. 9, p. e2912, Sep. 2017, https://doi.org/10.1002/cem.2912

Publisher
H. Shao, H. Jiang, X. Zhang, and M. Niu, “Rolling bearing fault diagnosis using an optimization deep belief network,” Measurement Science and Technology, Vol. 26, No. 11, p. 115002, Nov. 2015, https://doi.org/10.1088/0957-0233/26/11/115002

Publisher
H. Liu, J. Zhou, Y. Zheng, W. Jiang, and Y. Zhang, “Fault diagnosis of rolling bearings with recurrent neural network-based autoencoders,” ISA Transactions, Vol. 77, pp. 167–178, Jun. 2018, https://doi.org/10.1016/j.isatra.2018.04.005

Publisher
W. Fuan, J. Hongkai, S. Haidong, D. Wenjing, and W. Shuaipeng, “An adaptive deep convolutional neural network for rolling bearing fault diagnosis,” Measurement Science and Technology, Vol. 28, No. 9, p. 095005, Sep. 2017, https://doi.org/10.1088/1361-6501/aa6e22

Publisher
S. Mandal, B. Santhi, S. Sridhar, K. Vinolia, and P. Swaminathan, “Nuclear power plant thermocouple sensor fault detection and classification using deep learning and generalized likelihood ratio test,” IEEE Transactions on Nuclear Science, Vol. 64, No. 6, pp. 1–1, 2017, https://doi.org/10.1109/tns.2017.2697919

Publisher
V. Veerasamy et al., “LSTM recurrent neural network classifier for high impedance fault detection in solar PV integrated power system,” IEEE Access, Vol. 9, pp. 32672–32687, 2021, https://doi.org/10.1109/access.2021.3060800

Publisher
M. Liang, Y. Wang, X. Wu, L. Qian, and L. Chen, “Fault recognition of rolling bearing with small-scale dataset based on transfer learning,” Journal of Vibroengineering, Vol. 23, No. 5, pp. 1160–1170, Aug. 2021, https://doi.org/10.21595/jve.2021.21784

Publisher
J. Grezmak, J. Zhang, P. Wang, and R. X. Gao, “Multi-stream convolutional neural network-based fault diagnosis for variable frequency drives in sustainable manufacturing systems,” Procedia Manufacturing, Vol. 43, pp. 511–518, 2020, https://doi.org/10.1016/j.promfg.2020.02.181

Publisher
I. Mukherjee and S. Tallur, “Light-weight CNN enabled edge-based framework for machine health diagnosis,” IEEE Access, Vol. 9, pp. 84375–84386, 2021, https://doi.org/10.1109/access.2021.3088237

Publisher
P. Kumar and A. Shankar Hati, “Convolutional neural network with batch normalisation for fault detection in squirrel cage induction motor,” IET Electric Power Applications, Vol. 15, No. 1, pp. 39–50, Jan. 2021, https://doi.org/10.1049/elp2.12005

Publisher
I. Lomov, M. Lyubimov, I. Makarov, and L. E. Zhukov, “Fault detection in Tennessee Eastman process with temporal deep learning models,” Journal of Industrial Information Integration, Vol. 23, p. 100216, Sep. 2021, https://doi.org/10.1016/j.jii.2021.100216

Publisher
Zhu et al., “Fault diagnosis for rolling element bearings based on multi-sensor signals and CNN,” (in Chinese), Vibration and Shock, Vol. 39, pp. 172–178, 2020, https://doi.org/10.13465/j.cnki.jvs.2020.04.022

Publisher
Liu et al., “Real-time anti-noise fault diagnosis algorithm of one-dimensional convolutional neural network,” (in Chinese), Journal of Harbin Institute of Technology, Vol. 51, No. 7, pp. 89–95, 2019, https://doi.org/10.11918/j.issn.0367-6234.201809020

Publisher
Q. Niu, “Discussion on fault diagnosis of and solution seeking for rolling bearing based on deep learning,” Academic Journal of Manufacturing Engineering, Vol. 16, No. 1, pp. 58–64, 2018.

Search CrossRef
K. He, X. Zhang, S. Ren, and J. Sun, “Deep residual learning for image recognition,” in 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pp. 770–778, Jun. 2016, https://doi.org/10.1109/cvpr.2016.90

Publisher
K. He, X. Zhang, S. Ren, and J. Sun, “Identity mappings in deep residual networks,” in Computer Vision – ECCV 2016, pp. 630–645, 2016, https://doi.org/10.1007/978-3-319-46493-0_38

Publisher
H. Zhao, F. Liu, H. Zhang, and Z. Liang, “Research on a learning rate with energy index in deep learning,” Neural Networks, Vol. 110, pp. 225–231, Feb. 2019, https://doi.org/10.1016/j.neunet.2018.12.009

Publisher
Yang et al., “Improved CNN algorithm based on Dropout and ADAM optimizer,” (in Chinese), Journal of Huazhong University of Science and Technology, Vol. 46, No. 7, pp. 122–127, 2018, https://doi.org/10.13245/j.hust.180723

Publisher
P. Christoffersen and K. Jacobs, “The importance of the loss function in option valuation,” Journal of Financial Economics, Vol. 72, No. 2, pp. 291–318, May 2004, https://doi.org/10.1016/j.jfineco.2003.02.001

Publisher
H. Shao, D. Xu, and G. Zheng, “Convergence of a batch gradient algorithm with adaptive momentum for neural networks,” Neural Processing Letters, Vol. 34, No. 3, pp. 221–228, Dec. 2011, https://doi.org/10.1007/s11063-011-9193-x

Publisher
Duchi John C., E. Hazan, and Y. Singer, “Adaptive subgradient methods for online learning and stochastic optimization,” Journal of Machine Learning Research, Vol. 12, pp. 2121–2159, 2011.

Search CrossRef
S. Postalcıoğlu, “Performance analysis of different optimizers for deep learning-based image recognition,” International Journal of Pattern Recognition and Artificial Intelligence, Vol. 34, No. 2, p. 2051003, Feb. 2020, https://doi.org/10.1142/s0218001420510039

Publisher
Z. Chang, Y. Zhang, and W. Chen, “Electricity price prediction based on hybrid model of Adam optimized LSTM neural network and wavelet transform,” Energy, Vol. 187, p. 115804, Nov. 2019, https://doi.org/10.1016/j.energy.2019.07.134

Publisher
R. K. Yadav and Anubhav, “PSO-GA based hybrid with Adam optimization for ANN training with application in Medical Diagnosis,” Cognitive Systems Research, Vol. 64, pp. 191–199, Dec. 2020, https://doi.org/10.1016/j.cogsys.2020.08.011

Publisher
A. Rehman and T. Saba, “Neural networks for document image preprocessing: state of the art,” Artificial Intelligence Review, Vol. 42, No. 2, pp. 253–273, Aug. 2014, https://doi.org/10.1007/s10462-012-9337-z

Publisher
D. Zachariah and P. Stoica, “Online hyperparameter-free sparse estimation method,” IEEE Transactions on Signal Processing, Vol. 63, No. 13, pp. 3348–3359, Jul. 2015, https://doi.org/10.1109/tsp.2015.2421472

Publisher
M. A. Marins, F. M. L. Ribeiro, S. L. Netto, and E. A. B. Da Silva, “Improved similarity-based modeling for the classification of rotating-machine failures,” Journal of the Franklin Institute, Vol. 355, No. 4, pp. 1913–1930, Mar. 2018, https://doi.org/10.1016/j.jfranklin.2017.07.038

Publisher
W. A. Smith and R. B. Randall, “Rolling element bearing diagnostics using the Case Western Reserve University data: A benchmark study,” Mechanical Systems and Signal Processing, Vol. 64-65, pp. 100–131, Dec. 2015, https://doi.org/10.1016/j.ymssp.2015.04.021

Publisher
Ron Kohavi, “A study of cross-validation and bootstrap for accuracy estimation and model selection,” in IJCAI’95: Proceedings of the 14th international joint conference on Artificial intelligence, pp. 1137–1145, Jan. 1995.

Search CrossRef
Laurens van der Maaten and Geoffrey Hinton, “Visualizing data using t-SNE,” Journal of Machine Learning Research, Vol. 9, No. 86, pp. 2579–2605, 2008.

Search CrossRef
D. Li, F. Yang, and X. Wang, “Study on ensemble crop information extraction of remote sensing images based on SVM and BPNN,” Journal of the Indian Society of Remote Sensing, Vol. 45, No. 2, pp. 229–237, Apr. 2017, https://doi.org/10.1007/s12524-016-0597-y

Publisher

Cited by

A web-based intelligent calculator for predicting viscosity of ethylene–glycol–based nanofluids using an artificial neural network model

Walaeddine Maaoui | Zouhaier Mehrez | Mustapha Najjari

(2024)

Downscaling Daily Reference Evapotranspiration Using a Super-Resolution Convolutional Transposed Network

(2024)

Detection of car parking space by using Hybrid Deep DenseNet Optimization algorithm

Vankadhara Rajyalakshmi | Kuruva Lakshmanna

(2024)

Deep Learning for Sensing Matrix Prediction in Computational Microwave Imaging With Coded-Apertures

(2024)

Spatiotemporal prediction of particulate matter concentration based on traffic and meteorological data

Jiayu Yang | Linchang Shi | Jaeyoung Lee | Ingon Ryu

(2024)

Rapid prediction of particle-scale state-of-lithiation in Li-ion battery microstructures using convolutional neural networks

Sam Ly | Mohammad Amin Sadeghi | Niloofar Misaghian | Hamed Fathiannasab | Jeff Gostick

(2024)

A review on convolutional neural network in rolling bearing fault diagnosis

(2024)

2024 IEEE International Conference on Artificial Intelligence and Mechatronics Systems (AIMS)

Haniah Mahmudah | Syamsul Arifin | Aulia Siti Aisjah | Catur Arif Prastyanto

(2024)

Classification of Distributed Bearing Faults Using a Novel Sensory Board and Deep Learning Networks With Hybrid Inputs

Ramin Rajabioun | Mojtaba Afshar | Özkan Atan | Mutlu Mete | Bilal Akin

(2024)

Attempted movement classification of spinal cord injured patients using hybrid CNN‐LSTM networks

Kumar Shrestha | Md. Asadur Rahman | Pritom Kumar Saha | Mohd Abdur Rashid | Hiroki Higa

(2024)

Most influential feature form for supervised learning in voltage sag source localization

Younes Mohammadi | Boštjan Polajžer | Roberto Chouhy Leborgne | Davood Khodadad

(2024)

A comparative study on ensemble soft-computing methods for geothermal power production potential forecasting

Raif Kenanoğlu | İlker Mert | Ceyhun Baydar | Özkan Köse | Hüseyin Yağlı

(2024)

Interpretable SHAP Model Combining Meta-learning and Vision Transformer for Lithology Classification Using Limited and Unbalanced Drilling Data in Well Logging

Youzhuang Sun | Shanchen Pang | Zhiyuan Zhao | Yongan Zhang

(2024)

Drive-by scour damage detection in railway bridges using deep autoencoder and different sensor placement strategies

Thiago Fernandes | Rafael Lopez | Diogo Ribeiro

(2024)

ECOC-based integrated learning method for fault diagnosis in nuclear power plants

Guimin Sheng | Yu Mu | Boyang Zhang

(2024)

Integrating deep learning for phenomic and genomic predictive modeling of Eucalyptus trees

Freddy Mora-Poblete | Daniel Mieres-Castro | Antônio Teixeira do Amaral Júnior | Matías Balach | Carlos Maldonado

(2024)

An incipient fault diagnosis method based on Att-GCN for analogue circuits

Jingli Yang | Ye Li | Tianyu Gao

(2023)

Induction Motor Bearing Fault Diagnosis Based on Singular Value Decomposition of the Stator Current

Yuriy Zhukovskiy | Aleksandra Buldysko | Ilia Revin

(2023)

2023 2nd International Conference on Applied Artificial Intelligence and Computing (ICAAIC)

Vanita G. Tonge | Asha Ambhaikar

(2023)

Deep learning-driven end-to-end segmentation of Martian river valleys

Jian Ding | Jin Liu | Xiaolin Ning | Mingzhen Gui | Zhiwei Kang

(2023)

Heart rate estimation from ballistocardiogram signals processing via low-cost telemedicine architectures: a comparative performance evaluation

Adriano Tramontano | Oscar Tamburis | Salvatore Cioce | Salvatore Venticinque | Mario Magliulo

(2023)

Threat Detection Model for WLAN of Simulated Data Using Deep Convolutional Neural Network

Omar I. Dallal Bashi | Shymaa Mohammed Jameel | Yasir Mahmood Al Kubaisi | Husamuldeen K. Hameed | Ahmad H. Sabry

(2023)

Segmentation and classification of skin lesions using hybrid deep learning method in the Internet of Medical Things

Arslan Akram | Javed Rashid | Muhammad Arfan Jaffar | Muhammad Faheem | Riaz ul Amin

(2023)

2023 Eighth International Conference on Informatics and Computing (ICIC)

Syahida Usama Firdaus | Silvy Zafira Putri | Lailil Muflikhah | Pradiptya Kahvi Sugiharto

(2023)

Detection of the rotator cuff tears using a novel convolutional neural network from magnetic resonance image (MRI)

Mohammad Amin Esfandiari | Mohammad Fallah Tafti | Nader Jafarnia Dabanloo | Fereshteh Yousefirizi

(2023)

2023 Second International Conference on Electronics and Renewable Systems (ICEARS)

Venkata Sai Vutukuri | Swapna Regulagadda | Lokesh Chowdary Jasti | Abhinav Cheekurthi

(2023)

SensorSCAN: Self-supervised learning and deep clustering for fault diagnosis in chemical processes

Maksim Golyadkin | Vitaliy Pozdnyakov | Leonid Zhukov | Ilya Makarov

(2023)

A Deep Learning LSTM Approach to Predict COVD-19 Deaths in North Africa

Sami Khedhiri

(2023)

Multilingual Machine Translation System Based on Decoder Recurrent Neural Network

Fei Deng | Balakrishnan Nagaraj

(2022)

A new lightweight deep neural network for surface scratch detection

Wei Li | Liangchi Zhang | Chuhan Wu | Zhenxiang Cui | Chao Niu

(2022)

Research on an intelligent diagnosis method of mechanical faults for small sample data sets

(2022)

About this article

Received

26 October 2021

Accepted

11 February 2022

Published

30 June 2022

SUBJECTS

Fault diagnosis based on vibration signal analysis

DOI

https://doi.org/10.21595/jve.2022.22271

Keywords

Adam optimizer

bearing fault diagnosis

convolutional neural network

identity mapping

Acknowledgements

This work was supported by the Key Research and Development Program of Shaanxi Province of China (2022SF-259). It was also supported by the graduate student innovation fund of Xi’an University of Post and Telecommunications (CXJJLZ202016).

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2023 08 01

A fault diagnosis method based on dilated convolution and attention for rolling bearing under multiple working conditions and noisy environments

Hui Zhang, Shengdong Liu, Ziwei Lv, Zhenlong Sang, Fangning Li

Research article

2022 10 21

Bearing fault diagnosis method based on Gramian angular field and ensemble deep learning

Yanfang Han, Baozhu Li, Yingkun Huang, Liang Li

Research article

2021 05 11

Fault recognition of rolling bearing with small-scale dataset based on transfer learning

Ying Wang, Mingxuan Liang, Xiangwei Wu, Lijuan Qian, Li Chen

Research article

2020 08 15

Bearing fault diagnosis based on improved VMD and DCNN

Ran Wang, Lei Xu, Fengkai Liu

Y. Wang, Z. Xiao, and G. Cao, “A convolutional neural network method based on Adam optimizer with power-exponential learning rate for bearing fault diagnosis,” Journal of Vibroengineering, Vol. 24, No. 4, pp. 666–678, Jun. 2022, https://doi.org/10.21595/jve.2022.22271

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jve.2022.22271
UR  - https://doi.org/10.21595/jve.2022.22271
TI  - A convolutional neural network method based on Adam optimizer with power-exponential learning rate for bearing fault diagnosis
T2  - Journal of Vibroengineering
AU  - Wang, Youming
AU  - Xiao, Zhao
AU  - Cao, Gongqing
PY  - 2022
DA  - 2022/06/30
PB  - JVE International Ltd.
SP  - 666-678
VL  - 24
IS  - 4
SN  - 1392-8716
SN  - 2538-8460
ER  - 

Copy Ris

Copied to clipboard!

@article{Wang_2022,
	doi = {10.21595/jve.2022.22271},
	url = {https://doi.org/10.21595/jve.2022.22271},
	year = 2022,
	month = {mar},
	publisher = {{JVE} International Ltd.},
	volume = {24},
	number = {4},
	pages = {666--678},
	author = {Youming Wang and Zhao Xiao and Gongqing Cao},
	title = {A convolutional neural network method based on Adam optimizer with power-exponential learning rate for bearing fault diagnosis},
	journal = {Journal of Vibroengineering}
}

Copy Bibtex

Copied to clipboard!

[1]Y. Wang, Z. Xiao, and G. Cao, “A convolutional neural network method based on Adam optimizer with power-exponential learning rate for bearing fault diagnosis,” Journal of Vibroengineering, vol. 24, no. 4, pp. 666–678, Mar. 2022, doi: 10.21595/jve.2022.22271.

Copy IEEE

Copied to clipboard!

Wang, Youming, Zhao Xiao, and Gongqing Cao. “A Convolutional Neural Network Method Based on Adam Optimizer with Power-Exponential Learning Rate for Bearing Fault Diagnosis.” Journal of Vibroengineering 24, no. 4 (March 16, 2022): 666–78. https://doi.org/10.21595/jve.2022.22271.

Copy Chicago

Copied to clipboard!

A convolutional neural network method based on Adam optimizer with power-exponential learning rate for bearing fault diagnosis

Abstract

Highlights

1. Introduction

2. Convolutional neural network model based fault diagnosis

2.1. Adam optimizer with power-exponential learning rate

2.2. Convolutional neural network with improved Adam algorithm and identity mapping

3. Experimental results

3.1. Data acquisition

3.2. Data preprocessing

3.3. MaFaulDa bearing dataset fault diagnosis result analysis

3.4. CWRU bearing dataset fault diagnosis result analysis

4. Conclusions

References

Cited by

About this article

Related Articles