Numerical study on sloshing in coaxial shells

1. Introduction

The term “sloshing in tanks” describes a phenomenon in which the movement of the liquid inside a tank causes oscillations because of outside forces operating on the tank. This can happen in a variety of tanks, such as water or fuel tanks, or even cargo tanks inside space vessels or ships. Shells and structures resembling shells are prevalent components in contemporary mechanical engineering. These structures are frequently employed as fuel tanks for launch vehicles, reservoirs for storing fresh water, and other substances, including potentially hazardous explosives. When these tanks are subjected to substantial loads, there is a risk of intensive liquid sloshing, resulting in highly perilous consequences. It's important to highlight that the development of each new launch vehicle necessitates the design of novel fuel tanks.

A variety of tank designs are considered to discuss sloshing [1], [2]. Most common methods to discuss sloshing are BEM [3], FEM [4], FVM [5], and series expansions [6]. Many studies on modal analysis and frequencies have been reported in previous studies such as [2], [7], and [8]. Studies [9], [10] and [11] are devoted to developing analytical methods to analyze sloshing. Studies involving the theoretical and experimental aspects of the stability of tanks are reported in [12], [13] and [19].

The design and manufacture of new powerful launch vehicles necessitate the development of new fuel tanks. Currently, such tanks increasingly take the form of compound shells. To mitigate undesirable resonant frequencies, it is necessary to study the entire frequency spectrum of the tank's inherent vibrations, specifically under various fuel fill levels and different levels of loading. It is necessary to estimate the natural frequencies of empty tanks, the frequencies of elastic wall oscillations in the presence of liquid, as well as the sloshing frequencies. However, the investigation of vibrations of compound shells with compartments partially filled with liquid has not received sufficient attention in the literature [14]. Therefore, the study of vibrations of compound coaxial cylindrical and cylindrical-conical shells with liquid is a relevant scientific task.

2. Methodology

BEM is computationally efficient compared to other methods like the finite element method (FEM) or finite difference method (FDM), it can still be resource-intensive for large-scale engineering problems. To further reduce the computational cost of the boundary element method, several techniques and variations have been developed. One such technique is the “reduced” boundary element method, which aims to reduce the dimensionality of the problem or to simplify the computation further.

The main objective of this research lies in developing an efficient numerical method based on reduced boundary element (BEM) method to assess the sloshing frequencies of vibrations in compound liquid-filled reservoirs.

3. Problem statement

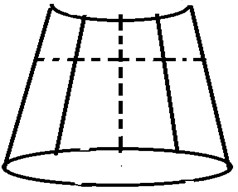
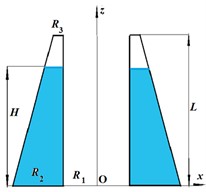
The geometry of the problem is shown in Fig. 1. $S_0$ and $S_1$ denote the free surface of the liquid and wetted surface of the shell respectively. An ideal and incompressible fluid is assumed to perform the motion inside the shells.

Fig. 1Сylindrical – conical compound shells

The following boundary value problem is formulated as follows:

Here the unknown function $\zeta =\zeta \left(t,x,y\right)$ characterizes the variations in position and shape of the free surface over time. So, it is necessary to determine the unknown functions $\mathrm{\Phi }$ and $\zeta$.

The unknown functions $\zeta$ and $\mathrm{\Phi }$ in cylindrical coordinates $\left(r,\theta ,z\right)$are expressed as:

Here time-dependent coefficients $d_k\left(t\right)$ are unknown. From Eq. (1), the basic functions ${\zeta }_k\left(r,\theta \right)$ and ${\phi }_k\left(r,\theta ,z\right)$are solutions to such a linear spectral boundary value problem:

where ${\chi }_k$ are fundamental frequencies. As it has been shown in [3], for shells of revolution, all unknown functions for each wave number $l$ can be expressed in the following form:

Such presentation simplifies the analysis by reducing the problem to a series of uncoupled single-degree-of-freedom systems, depending on $l$, making the numerical estimations computationally more efficient. Moreover, for the shells of revolution, reduced finite and boundary element methods can be applied.

4. Results and discussion

5. Conclusions

The reduced boundary element method for sloshing analysis in coaxial shells shell structures partially filled with liquid is used to calculate frequencies. The spectral boundary problem for the liquid vibrations in rigid shells is solved. The mode shapes are reported for the considered problem. The further intention is to consider forced vibrations at different levels of gravity [6].

Fig. 2Sloshing modes φkr,θ, H

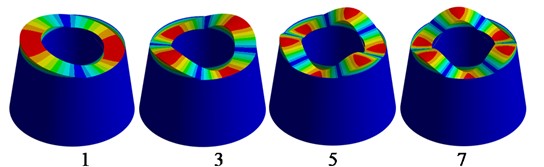
a) Sloshing modes of shell structure Fig. 1(a)

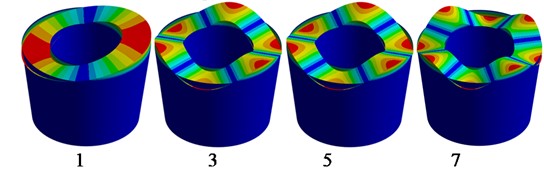
b) Sloshing modes of shell structure Fig. 1(b)