Vibrational frequency of triangular plate having circular thickness

Lather, Neeraj; Kumar, Ankit; Yadav, Parvesh; Bhardwaj, Reeta; Sharma, Amit

doi:10.21595/vp.2023.23370

Vibroengineering Procedia

Browse Procedia

Published: 25 November 2023

Check for updates

Vibrational frequency of triangular plate having circular thickness

Neeraj Lather¹

Ankit Kumar²

Parvesh Yadav³

Reeta Bhardwaj⁴

Amit Sharma⁵

^{1, 3, 4, 5}Department of Mathematics, Amity University Haryana, Gurugram, India

²Chitkara University School of Engineering and Technology, Chitkara University, Himachal Pardesh, India

Corresponding Author:

Amit Sharma

Cite the article Download PDF

Abstract

In the current research, modes of frequency of isotropic tapered triangular plate having 1-D (one dimensional) circular thickness and 1-D (one dimensional) linear temperature profile for clamped boundary conditions are discussed. Authors implemented Rayleigh Ritz technique to solve the frequency equation of isotropic triangular plate and computed the first four modes with a distinct combination of plate parameters. Authors have performed the convergence study of modes of frequency of the isotropic triangular plate. Also, conducted comparative analysis of modes of frequency of the current study with available published papers and the results presented in tabular form. The aim of the present study is to show the impact of a one dimensional circular thickness and one dimensional linear temperature on modes of frequency of vibration of an isotropic tapered triangular plate.

1. Introduction

Now a days, study of vibration of nonuniform plates is very essential because vibration plays significantly role in many engineering applications i.e., nuclear reactor, aeronautical field, submarine etc. Study of vibration of triangular plates with variable thickness and temperature has been carried out by many researchers/scientists and has been reported in literature. but till date to the best of the knowledge of the authors, vibration of triangular plate with one dimensional circular thickness has not been considered yet.

Free vibration of cantilevered and completely free isosceles triangular plates based on exact three-dimensional elasticity theory has been investigated in [1] and derived the eigen frequency equation by using Rayleigh Ritz method. Chebyshevs Ritz method is applied in [2] to the free in plane vibration of arbitrary shaped laminated triangular plates with elastic boundary conditions. Time period analysis of isotropic and orthotropic visco skew plate having circular variation in thickness and density at different edge conditions is discussed in [3] and [4]. Two dimensional temperature effect on the vibration is computed in [5] for the first time for a clamped triangular plate with two dimensional thickness by using the Rayleigh Ritz method. A unified formulation was proposed in [6] for the free in-plane vibration of arbitrarily shaped straight-sided quadrilateral and triangular plates with arbitrary boundary conditions by improved Fourier series method (IFSM). Fourier series method is used in [7] for free vibration of arbitrary shaped laminated triangular thin plates. A computationally efficient and accurate numerical model is presented in [8] for the study of free vibration behavior of anisotropic triangular plates with edges elastically restrained against rotation and translation. Free vibration of thick equilateral triangular plates with classical boundary conditions has been investigated in [9] based on a new shear deformation theory. Free vibration of circular and annular three-dimensional graphene foam (3D-GrF) plates under various boundary conditions is discussed in [10].

From the above literature, it is evident that till date to the best of the knowledge of the authors, none of the researchers have worked on triangular plate with one dimensional circular thickness and one dimensional linear temperature environment for clamped boundary conditions. Therefore, in this present study we aim to study the above mentioned problem and investigate the impact on frequency modes of the plate The main purpose of the present study to provide a mathematical model for analyzing the effect of 1-D circular variation in thickness on frequency modes of triangular plate under 1-D linear temperature variation, which had not been investigated earlier. All the numerical results in the form of modes of frequency are presented in tabular form.

2. Problem geometry and analysis

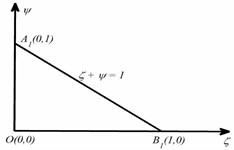
Consider a viscoelastic triangle plate having aspect ratio $θ = b / c$ and $μ = c / a$ and one dimensional thickness $l$ as shown in Fig. 1. Now transform the given triangle into right-angled triangle using the transformation $x = a ζ + b ψ$ and $y = c ψ$ as shown in Fig. 2.

Fig. 1Triangle plate

Fig. 2Transformed triangle plate

The kinetic energy and strain energy for vibration of a triangle plate are taken as in [11]:

1

T_{s} = \frac{1}{2} ρ ω^{2} \int_{0}^{1} \int_{0}^{1 - ζ} Φ^{2} a c d ψ d ζ,

2

V_{s} = \frac{1}{2} \int_{0}^{1} \int_{0}^{1 - ζ} D_{1} [\frac{1}{a^{4}} {(\frac{\partial^{2} Φ}{\partial ζ^{2}})}^{2} + {(\frac{b^{2}}{a^{2} c^{2}} \frac{\partial^{2} Φ}{\partial ζ^{2}} + \frac{1}{c^{2}} \frac{\partial^{2} Φ}{\partial ψ^{2}} - \frac{2 b}{a c^{2}} \frac{\partial^{2} Φ}{\partial ζ \partial ψ})}^{2} + 2 v (\frac{1}{a^{2}} \frac{\partial^{2} Φ}{\partial ζ^{2}})

+ (\frac{b^{2}}{a^{2} c^{2}} \frac{\partial^{2} Φ}{\partial ζ^{2}} + \frac{1}{c^{2}} \frac{\partial^{2} Φ}{\partial ψ^{2}} - \frac{2 b}{a c^{2}} \frac{\partial^{2} Φ}{\partial ζ \partial ψ}) + 2 (1 - ν) {(- \frac{b}{a^{2} c} \frac{\partial^{2} Φ}{\partial ζ^{2}} + \frac{1}{a c^{2}} \frac{\partial^{2} Φ}{\partial ζ \partial ψ})}^{2}] a c d ψ d ζ,

where $Φ$ is the deflection function and $D_{1} = E^{3} / 12 (1 - ν^{2})$ is flexural rigidity.

The Rayleigh Ritz method requires:

3

L = δ (V_{s} - T_{s}) = 0 .

Using Eqs. (1) and (2), we have:

4

L = \frac{1}{2} \int_{0}^{1} \int_{0}^{1 - ζ} D_{1} [\frac{1}{a^{4}} {(\frac{\partial^{2} Φ}{\partial ζ^{2}})}^{2} + {(\frac{b^{2}}{a^{2} c^{2}} \frac{\partial^{2} Φ}{\partial ζ^{2}} + \frac{1}{c^{2}} \frac{\partial^{2} Φ}{\partial ψ^{2}} - \frac{2 b}{a c^{2}} \frac{\partial^{2} Φ}{\partial ζ \partial ψ})}^{2} + 2 v (\frac{1}{a^{2}} \frac{\partial^{2} Φ}{\partial ζ^{2}})

+ (\frac{b^{2}}{a^{2} c^{2}} \frac{\partial^{2} Φ}{\partial ζ^{2}} + \frac{1}{c^{2}} \frac{\partial^{2} Φ}{\partial ψ^{2}} - \frac{2 b}{a c^{2}} \frac{\partial^{2} Φ}{\partial ζ \partial ψ}) + 2 (1 - ν) {(- \frac{b}{a^{2} c} \frac{\partial^{2} Φ}{\partial ζ^{2}} + \frac{1}{a c} \frac{\partial^{2} Φ}{\partial ζ \partial ψ})}^{2}] a c d ψ d ζ

- \frac{1}{2} ρ ω^{2} \int_{0}^{1} \int_{0}^{1 - ζ} l Φ^{2} a c d ψ d ζ .

Introducing one dimensional circular thickness as:

5

l = l_{0} (1 + β \{1 - \sqrt{1 - ζ^{2}}\}),

where $l_{0}$ are the thickness at origin. Also $β$ is tapering parameter.

One dimensional temperature on the plate is assumed to be linear as:

6

τ = τ_{0} (1 - ζ),

where $τ$ and $τ_{0}$ denote the temperature on and at the origin respectively.

The modulus of elasticity is given by:

7

E = E_{0} (1 - γ τ),

where $E_{0}$ is the Young’s modulus at $τ = 0$ , and $γ$ is called the slope of variation. Using Eq. (6) and Eq. (7) becomes:

8

E = E_{0} (1 - α (1 - ζ)),

where $α = γ τ_{0}$ , $(0 \leq α < 1)$ is called thermal gradient. Using Eqs. (5) and (8), the functional in Eq. (4) becomes:

9

L = \int_{0}^{1} \int_{0}^{1 - ζ} [(1 - α (1 - ζ)) {(1 + β \{1 - \sqrt{1 - ζ^{2}}\})}^{3} {(1 + θ^{2})}^{2} {(\frac{\partial^{2} Φ}{\partial ζ^{2}})}^{2}

+ {(\frac{\partial^{2} Φ}{\partial ψ^{2}})}^{2} \frac{2 (2 θ^{2} + 1 - ν)}{μ^{2}} {(\frac{\partial^{2} Φ}{\partial ζ \partial ψ})}^{2} + \frac{2 (ν + θ^{2})}{μ^{2}} (\frac{\partial^{2} Φ}{\partial ζ^{2}}) (\frac{\partial^{2} Φ}{\partial ψ^{2}})

- \frac{4 θ (1 + θ^{2})}{μ} (\frac{\partial^{2} Φ}{\partial ζ^{2}}) (\frac{\partial^{2} Φ}{\partial ζ \partial ψ}) - \frac{4 θ}{μ^{3}} (\frac{\partial^{2} Φ}{\partial ψ^{2}}) (\frac{\partial^{2} Φ}{\partial ζ \partial ψ})] a c d ψ d ζ

- \frac{1}{2} ρ ω^{2} \int_{0}^{1} \int_{0}^{1 - ζ} (1 + β \{1 - \sqrt{1 - ζ^{2}}\}) Φ^{2} a c d ψ d ζ .

where $D_{0} = E_{0} l_{0}^{3} / 12 (1 - v^{2})$ and $λ^{2} = ρ ω^{2} l_{0} a^{2} / D_{0}$ .

The deflection function is taken as:

10

Φ (ζ, ψ) = [(ζ)^{e} (ψ)^{f} (1 - ζ - ψ)^{g}] [\sum_{i = 1}^{n} Ψ_{i} {(ζ) (ψ) (1 - ζ - ψ)}^{i}],

where $Ψ_{i}$ , $i = 0,1, 2 \dots n$ are unknowns and the value of $e$ , $f$ , $g$ can be 0, 1 and 2 corresponding to a given edge condition.

To minimize Eq. (9), we have:

11

\frac{\partial L}{\partial Ψ_{i}} = 0, i = 0,1, \dots n .

Solving Eq. (11), we have frequency equation:

12

|P - λ^{2} Q| = 0,

where $P = {[p_{i j}]}_{i, j = 0,1, \dots n}$ and $Q = {[q_{i j}]}_{i, j = 0,1, \dots n}$ are the square matrix of order $(n + 1)$ .

3. Numerical results and discussion

In the current study, authors evaluated numerical data in the form of modes of frequency (first four modes) for right angled isosceles scalene triangular plate, right angled scalene triangular plate and scalene triangular plate on clamped edge condition for the different value of plate parameters. Throughout the calculation the value of aspect ratio $a / b =$ 1.5, Poisson’s ratio $ν =$ 0.345, $E_{0} =$ 2.80·10³N/M² and $ρ =$ 2.80·10³kg/M³ is taken into consideration. All the results are presented in tabular form (refer Tables 1-3). Table 1 presents the modes of frequency $λ$ for right angled isosceles triangular plate corresponding to tapering parameter $β$ for fixed value of $θ =$ 0, $μ =$ 1.0 and the variable value of thermal gradient $α$ i.e., $α =$ 0.2, 0.6. From the Table 1, it can be seen that the modes of frequency $λ$ decreases with the increasing value of tapering parameter $β$ for all the above mentioned value of thermal gradient $α$ . It is also observed that the value modes of frequency $λ$ decreases with the increasing value of thermal gradient $α$ , while the rate of decrement in modes of frequency $λ$ increases with the increasing value of thermal gradient $α$ .

Table 2 incorporates the modes of frequency $λ$ for right angled scalene triangular plate corresponding to tapering parameter $β$ for fixed value of $θ =$ 0, $μ =$ 1.5 and the variable value of thermal gradient $α$ i.e., $α =$ 0.2, 0.6. In table 2 also, modes of frequency $λ$ decreases with the increasing value of tapering parameter $β$ for all the above mentioned value of thermal gradient $α$ as shown in Table 1. Like in Table 1, it is also observed in Table 2 that the value modes of frequency $λ$ decreases with the increasing value of thermal gradient $α$ , while the rate of decrement in modes of frequency $λ$ increases with the increasing value of thermal gradient $α$ .

Table 1Modes of frequency of right angle isosceles triangle plate corresponding to tapering parameter

$θ = 0$ , $μ = 1.0$
$α = 0.2$					$α = 0.6$
$β$	$λ_{1}$	$λ_{2}$	$λ_{3}$	$λ_{4}$	$λ_{1}$	$λ_{2}$	$λ_{3}$	$λ_{4}$
0.0	100.130	366.937	831.845	2127.902	84.6067	309.174	702.733	1815.61
0.2	97.9199	360.068	816.224	2063.28	82.5137	302.794	687.724	1753.50
0.4	95.7800	353.380	799.694	2024.049	80.4804	296.555	672.161	1712.71
0.6	93.7147	346.888	785.481	1958.46	78.5112	290.473	658.629	1649.75
0.8	91.7283	340.614	770.259	1916.75	76.6108	284.567	644.601	1606.46
1.0	89.8245	334.544	755.453	1883.44	74.7835	278.878	630.245	1571.98

Table 2Modes of frequency of right angle scalene triangle plate corresponding to tapering parameter

$θ =$ 0, $μ = 1.5$
$α = 0.2$					$α = 0.6$
$β$	$λ_{1}$	$λ_{2}$	$λ_{3}$	$λ_{4}$	$λ_{1}$	$λ_{2}$	$λ_{3}$	$λ_{4}$
0.0	90.3135	330.939	750.081	1917.22	76.1245	278.106	631.328	1626.59
0.2	88.3716	324.966	736.576	1861.97	74.2734	272.520	618.272	1573.02
0.4	86.4950	319.165	722.302	1829.51	72.4780	267.054	604.933	1538.14
0.6	84.6875	313.532	710.242	1773.00	70.7424	261.745	593.284	1483.65
0.8	82.9526	308.0911	697.482	1737.62	69.0705	256.601	581.116	1447.01
1.0	81.2937	302.856	684.760	1710.59	67.4662	251.626	569.113	1417.35

Table 3Modes of frequency of scalene triangle plate corresponding to tapering parameter

$θ = 1 / \sqrt{3}$ , $μ = \sqrt{3} / 2$
$α = 0.2$					$α = 0.6$
$β$	$λ_{1}$	$λ_{2}$	$λ_{3}$	$λ_{4}$	$λ_{1}$	$λ_{2}$	$λ_{3}$	$λ_{4}$
0.0	78.6772	289.064	654.766	1661.231	64.3411	237.763	538.269	1352.55
0.2	77.5677	285.1960	645.948	1632.17	63.2087	233.907	529.352	1321.08
0.4	76.5167	281.485	636.874	1618.99	62.1304	230.217	519.905	1303.43
0.6	75.5254	277.949	629.700	1584.65	61.1079	226.664	512.370	1268.33
0.8	74.5946	274.599	621.852	1569.17	60.1430	223.287	504.310	1248.69
1.0	73.7247	271.443	614.434	1554.99	59.2370	220.074	496.777	1230.15

Table 3 provides the modes of frequency $λ$ for scalene triangular plate corresponding to tapering parameter $β$ for fixed value of $θ = 1 / \sqrt{3}$ , $μ = \sqrt{3} / 2$ and the variable value of thermal gradient $α$ i.e., $α =$ 0.2, 0.6. In table 3 also, modes of frequency $λ$ decreases with the increasing value of tapering parameter $β$ for all the above mentioned value of thermal gradient $α$ as shown in Tables 1, 2. Like in Tables 1, 2, it is also reported in Table 3 that the value modes of frequency $λ$ decreases with the increasing value of thermal gradient $α$ , while the rate of decrement in modes of frequency $λ$ increases with the increasing value of thermal gradient $α$ .

4. Convergence study

In this section, authors shows the convergence study done on modes of frequency $λ$ (first two modes) of right angled isosceles scalene triangular plate, right angled scalene triangular plate and scalene triangular plate at clamped edge condition for the plate parameters specified as $α = β = 0.0$ , $ν =$ 0.345 and $a / b =$ 1.5. The results are displayed in tabular form (refer Table 4). From the Table 4, one can concluded that modes of frequency for the above mentioned triangular plates converges up to three decimal place in fifth approximation.

Table 4Modes of frequency of scalene triangle plate corresponding to tapering parameter

$N$	$θ = 0.0$ , $μ = 1.0$		$θ = 0.0$ , $μ = 1.5$		$θ = 1 / \sqrt{3}$ , $μ = \sqrt{3} / 2$
$N$	$λ_{1}$	$λ_{2}$	$λ_{1}$	$λ_{2}$	$λ_{1}$	$λ_{2}$
2	107.077	436.191	107.077	436.191	92.7314	377.753
3	107.046	394.917	96.6275	356.480	92.7048	342.008
4	107.045	392.630	96.6272	354.406	92.7045	340.018
5	107.045	392.630	96.6272	354.406	92.7045	340.018

Table 5Comparison of modes of frequency with [12] for right angled isosceles, right angled scalene and scalene triangular plate corresponding to tapering parameter

$α = 0.0$
$β$	$θ = 0.0$ , $μ = 1.0$		$θ = 0.0$ , $μ = 1.5$		$θ = 1 / \sqrt{3}$ , $μ = \sqrt{3} / 2$
$β$	$λ_{1}$	$λ_{2}$	$λ_{1}$	$λ_{2}$	$λ_{1}$	$λ_{2}$
0.0	107.077	436.192	96.665	393.737	84.965	346.119
	107.077	436.192	79.2171	322.7010	70.8248	288.5140
0.2	104.798	426.334	94.658	385.287	83.849	341.319
	98.813	401.130	74.1212	301.2510	66.7330	271.5330
0.4	102.595	416.894	92.731	377.213	82.792	336.839
	91.069	368.577	69.4564	281.9920	63.0304	256.6090
0.6	100.472	407.884	90.877	369.526	81.798	332.682
	83.983	339.162	65.3054	265.3940	59.7782	244.1390
0.8	98.432	284.632	89.099	362.233	80.865	328.853
	77.713	313.628	61.7481	251.9720	57.0324	234.5460
Bold values are obtained from [12]

5. Results comparison

In this section, authors performed a comparative analysis of modes of frequency $λ$ (first two modes) obtained in present study (right angled isosceles scalene triangular plate, right angled scalene triangular plate and scalene triangular plate) and modes of frequency $λ$ obtained in [12] at clamped edge condition and presented in tabular form (refer Table 5). In [12], authors assumed the thickness variations in both the direction but in the present study authors taken the thickness in one direction so authors compared the modes of frequency $λ$ of present study with modes of frequency $λ$ obtained in [12] when the value of second tapering parameter $β_{2}$ is 0.0 in [12]. Table 5 shows the comparison of modes of frequency $λ$ obtained in present study (right angled isosceles scalene triangular plate, right angled scalene triangular plate and scalene triangular plate) and modes of frequency $λ$ obtained in [12] at clamped edge condition corresponding to tapering parameter $β$ for fixed value of thermal gradient $α$ i.e., $α = 0.0$ . From the Table 5, authors conclude that:

1) Modes of frequency $λ$ obtained in present study (right angled isosceles scalene triangular plate, right angled scalene triangular plate and scalene triangular plate) are higher in comparison to modes of frequency $λ$ obtained in [12].

2) The rate of change in (decrement) in modes of frequency $λ$ obtained in present study (right angled isosceles scalene triangular plate, right angled scalene triangular plate and scalene triangular plate) are smaller in comparison to modes of frequency $λ$ obtained in [12], at clamped edge condition for all the three above mentioned values of thermal gradient $α$ .

6. Conclusions

The effect of circular thickness on modes of frequency $λ$ of right angled isosceles scalene triangular plate, right angled scalene triangular plate and scalene triangular plate under temperature environment at clamped edge condition is computed. Based on numerical discussions and results comparisons, authors would like to records the following facts:

1) The modes of frequency obtained in present study in case of circular thickness is higher than the modes of frequency obtained in [12] in case of linear thickness. The modes of frequency obtained in present study and modes of frequency obtained in [12] exactly match at $β = 0.0$ (refer Table 5).

2) The variation in modes of frequency obtained in present study in case of circular thickness is less in comparison to modes of frequency obtained in [12] in case of linear variation in thickness (refer Table 5).

3) The modes of frequency obtained for the present study decreases (less rate of decrements) with the increasing value of tapering parameter and thermal gradient. (refer Tables 1-3).

4) As temperature increases on the plate, the modes of frequency decreases but the rate of change (decrement) in modes of frequency increases (refer Tables 1-3).

References

Y. K. Cheung and D. Zhou, “Three-dimensional vibration analysis of cantilevered and completely free isosceles triangular plates,” International Journal of Solids and Structures, Vol. 39, No. 3, pp. 673–687, Feb. 2002, https://doi.org/10.1016/s0020-7683(01)00196-2

Publisher
D. He, T. Liu, B. Qin, Q. Wang, Z. Zhai, and D. Shi, “In-plane modal studies of arbitrary laminated triangular plates with elastic boundary constraints by the chebyshev-ritz approach,” Composite Structures, Vol. 271, p. 114138, Sep. 2021, https://doi.org/10.1016/j.compstruct.2021.114138

Publisher
A. Sharma, R. Bhardwaj, N. Lather, S. Ghosh, N. Mani, and K. Kumar, “Time period of thermal-induced vibration of skew plate with two-dimensional circular thickness,” Mathematical Problems in Engineering, Vol. 2022, pp. 1–12, Mar. 2022, https://doi.org/10.1155/2022/8368194

Publisher
N. Lather, R. Bhardwaj, A. Sharma, and K. Kumar, “Time period analysis of orthotropic skew plate with 2-d circular thickness and 1-d circular density,” Mathematical Problems in Engineering, Vol. 2022, pp. 1–15, Oct. 2022, https://doi.org/10.1155/2022/7880806

Publisher
A. Khodiya and A. Sharma, “Temperature effect on frequencies of a tapered triangular plate,” Journal of Applied Mathematics and Computational Mechanics, Vol. 20, No. 1, pp. 37–48, 2021.

Publisher
T. Liu, G. Hu, A. Wang, and Q. Wang, “A unified formulation for free in-plane vibrations of arbitrarily-shaped straight-sided quadrilateral and triangular thin plates,” Applied Acoustics, Vol. 155, pp. 407–422, Dec. 2019, https://doi.org/10.1016/j.apacoust.2019.06.014

Publisher
X. Lv and D. Shi, “Free vibration of arbitrary-shaped laminated triangular thin plates with elastic boundary conditions,” Results in Physics, Vol. 11, pp. 523–533, Dec. 2018, https://doi.org/10.1016/j.rinp.2018.09.003

Publisher
L. G. Nallim, B. M. Luccioni, and R. O. Grossi, “Vibration of general triangular composite plates with elastically restrained edges,” Thin-Walled Structures, Vol. 43, No. 11, pp. 1711–1745, Nov. 2005, https://doi.org/10.1016/j.tws.2005.07.002

Publisher
K. Pradhan and S. Chakraverty, “Natural frequencies of equilateral triangular plates under classical edge supports,” in Symposium on Statistical and Computational Modelling with Applications, 2016.

Search CrossRef
Y. Q. Wang and M. W. Teng, “Vibration analysis of circular and annular plates made of 3d graphene foams via Chebyshev-Ritz method,” Aerospace Science and Technology, Vol. 95, p. 105440, Dec. 2019, https://doi.org/10.1016/j.ast.2019.105440

Publisher
S. Chakraverty, Vibration of plates. CRC Press, 2008, https://doi.org/10.1201/9781420053968

Publisher
N. Kaur, “Vibrational behavior of tapered triangular plate with clamped ends under thermal condition,” Journal of The Institution of Engineers (India): Series C, Vol. 101, No. 2, pp. 391–399, Apr. 2020, https://doi.org/10.1007/s40032-019-00551-9

Publisher

About this article

Received

28 April 2023

Accepted

25 May 2023

Published

25 November 2023

SUBJECTS

Modal analysis and applications

DOI

https://doi.org/10.21595/vp.2023.23370

Keywords

Isotropic triangular plate

temperature

circular thickness

frequency

vibration

Acknowledgements

The authors have not disclosed any funding.

Data Availability

The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

Conflict of interest

The authors declare that they have no conflict of interest.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2019 11 28

Free vibration of circular annular plate with different boundary conditions

Yash Jaiman, Baij Singh

Research article

2019 03 15

Modelling on vibration of skew plate with thickness and temperature variation

Reeta Bhardwaj, Naveen Mani

Research article

2019 03 15

Vibration of rectangle plate with variable density and Poisson’s ratio

Amit Sharma, Vijay Kumar, Reeta Bhardwaj

Research article

2018 12 31

Vibration characteristic analysis of a circular thin plate with complex pre-stress distribution

Leixin Li, Luyun Chen, Hong Yi

N. Lather, A. Kumar, P. Yadav, R. Bhardwaj, and A. Sharma, “Vibrational frequency of triangular plate having circular thickness,” Vibroengineering Procedia, Vol. 52, pp. 67–73, Nov. 2023, https://doi.org/10.21595/vp.2023.23370

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/vp.2023.23370
UR  - https://doi.org/10.21595/vp.2023.23370
TI  - Vibrational frequency of triangular plate having circular thickness
T2  - Vibroengineering Procedia
AU  - Lather, Neeraj
AU  - Kumar, Ankit
AU  - Yadav, Parvesh
AU  - Bhardwaj, Reeta
AU  - Sharma, Amit
PY  - 2023
DA  - 2023/11/25
PB  - JVE International Ltd.
SP  - 67-73
VL  - 52
SN  - 2345-0533
SN  - 2538-8479
ER  - 

Copy Ris

Copied to clipboard!

 @article{Lather_2023, title={Vibrational frequency of triangular plate having circular thickness}, volume={52}, ISSN={2538-8479}, url={https://doi.org/10.21595/vp.2023.23370}, DOI={10.21595/vp.2023.23370}, journal={Vibroengineering Procedia}, publisher={JVE International Ltd.}, author={Lather, Neeraj and Kumar, Ankit and Yadav, Parvesh and Bhardwaj, Reeta and Sharma, Amit}, year={2023}, month=nov, pages={67–73} }

Copy Bibtex

Copied to clipboard!

[1]N. Lather, A. Kumar, P. Yadav, R. Bhardwaj, and A. Sharma, “Vibrational frequency of triangular plate having circular thickness,” Vibroengineering Procedia, vol. 52, pp. 67–73, Nov. 2023, doi: 10.21595/vp.2023.23370.

Copy IEEE

Copied to clipboard!

Lather, Neeraj, Ankit Kumar, Parvesh Yadav, Reeta Bhardwaj, and Amit Sharma. “Vibrational Frequency of Triangular Plate Having Circular Thickness.” Vibroengineering Procedia 52 (November 25, 2023): 67–73. https://doi.org/10.21595/vp.2023.23370.

Copy Chicago

Copied to clipboard!

Vibrational frequency of triangular plate having circular thickness

Abstract

1. Introduction

2. Problem geometry and analysis

3. Numerical results and discussion

4. Convergence study

5. Results comparison

6. Conclusions

References

About this article

Related Articles