Free vibration of circular annular plate with different boundary conditions

1. Introduction

Plates are widely used as a structural element and have vast practical applications in many engineering fields such as aerospace, mechanical, civil, nuclear, electronic, automotive, marine and heavy machinery, etc. Various researchers have analyzed the free vibration behavior of circular annular plates of different shapes, sizes, thickness for different boundary conditions. Leissa [1] used the Ritz method to estimate the natural frequencies of the isotropic plate for different boundary conditions. Kim and Dickinson [2] used the Rayleigh-Ritz approximation method for free vibration of a thin plate to extract natural frequencies. Rajalingham et al. [3] used a Rayleigh-Ritz method to analyze the plate characteristics parameter as shape functions and continued his work to formulate a variational reduction expression to analyze frequencies and mode shapes. Liew et al. [4] used the polynomials-Ritz method for the vibration of circular plates by using three-dimensional elasticity solutions. Zhou et al. [5] used the Chebyshev-Ritz method for three-dimensional vibration and mode shapes of the circular plate. Lim et al. [6] used the state-space method to analyze transverse vibration and mode of a thick circular plate. Zhou et al. [7] used the Hamiltonian principle to solve governing equations for free vibration analysis by using the variational principle of mixed energy method. Kumar et al. [8] use a dynamic stiffness method to extract the natural frequency and mode shapes of a thin plate. Piyush et al. [9] used the Rayleigh-Ritz method to compute the natural frequencies of the thin plate.

2. Basic formulation

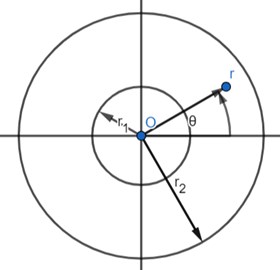
Consider a homogeneous, isotropic circular annular plate in cylindrical coordinates $\left(r,\theta ,z\right)$ with uniform thickness $h$ as shown in Fig. 1.

Classical plate theory is used to derive the governing differential equation for transverse vibration in the polar coordinate system is defined as:

where Laplacian operator: ${\nabla }^2=\frac{{\partial }^2}{{\partial r}^2}+\frac{1}{r}\frac{\partial }{\partial r}+\frac{1}{r^2}\frac{{\partial }^2}{{\partial \theta }^2}$, $\rho$ is the mass density, $D=E{h}^3/\left[12\left(1-{\nu }^2\right)\right]$ is the flexural rigidity and $\nu$ is Poisson’s ratio.

Transverse deflection of natural vibrations for thin circular plate is assumed to be:

where $\omega$ is the natural frequency and $w\left(r,\theta \right)$ is natural mode.

Substituting Eqs. (2) in (1), we get:

where:

The general finite element equation for the transverse deflection of thin plate is given by:

where $\left[M\right]$ is the mass matrix, $\left[K\right]$ is stiffness matrix, $\left\{\ddot{q}\right\}$ is the nodal acceleration vector, and $\left\{q\right\}$ is nodal displacement vector.

The non-dimension natural frequency parameter $\varpi$ are calculated as:

where $\omega$ is the natural frequency in Hz.

Fig. 1Schematic diagram and coordinate system of annular circular plate

3. Results and discussions

In this section, the first six non-dimensional natural frequencies and mode shapes of the circular annular plate are estimated by using the finite element method. Here, we calculated different eigenvalues for different boundary conditions with different radii ratio $(r_1/r_2)$. Different combinations of boundary conditions are applied to compute the natural frequencies and mode shapes of the circular annular plate. 2820 elements and 5922 nodes are used to estimate the natural frequencies and mode shape function of thin circular annular plates after convergence study. The present natural frequencies results are compared with those available in the literature.

Tables 1-4 shows that the first six non-dimensional natural frequencies values for the circular annular plate. These present results are nearly the same as Leissa [1] and Zhou [8] under different boundary conditions.

Fig. 2Natural modes of a clamped annular plate with a free inner boundary, r1/r2 = 0.4

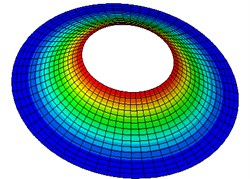
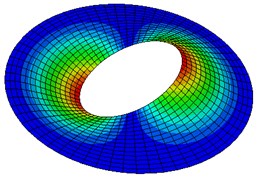
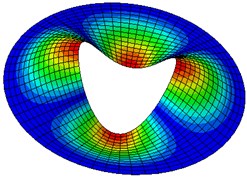
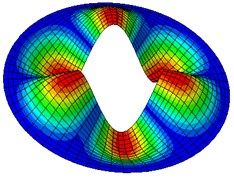
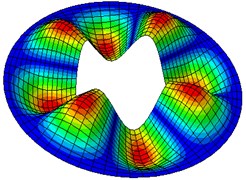
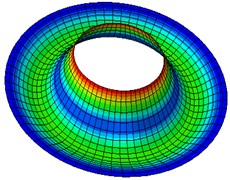
Table 5-7 presents the effect of the radii ratio on the non-dimensional frequency parameter of thin plates. It is observed from these tables that as the radii ratio increases non-dimensional frequency parameter increases.

4. Conclusions

In this paper, numerical analysis for free vibration analysis of a thin annular solid plate is carried out using the finite element method for different boundary conditions at the inner and outer radius. It is found that those natural frequency results are quite close to those reported in previous works of literature. The novelty of this paper is the effect of the radii ratio on natural frequency is discussed and found that with increasing radii ratio, natural frequency increases and another novelty is by using shell element modeling as per Abaqus convention the dimensionless frequency parameter as found in the literature are completely validated.