Nonlinear dynamic behavior analysis of bridge pier impacted by a moving barge

2.1. Barge and whole bridge model

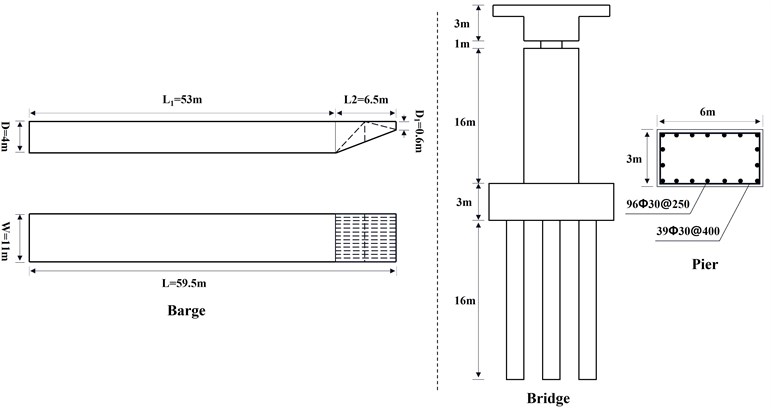
The total span of the whole bridge model used in this paper is 120 m. The bridge model consists of bridge deck, laminated rubber bearing (2 m×1 m×1 m), reinforced concrete pier (6 m×3 m×16 m), pile cap (13 m×10 m×3 m) and pile foundation (2 m in diameter and 16 m in length), as shown in Figs. 1-2. The pier contains steel reinforcement, and the steel reinforcement is modeled by separate method [8], without considering the bond and slip between steel reinforcement and concrete.

The ship type is flat bow barge. The barge model is established according to the size and structure of JH type barge in AASHTO specification [9]-[10]. For the convenience of calculation, the complex internal structure of the bow is simplified to multi-layer trusses. The specific dimensions are shown in Fig. 1.

Fig. 1Dimension diagram of barge and whole bridge

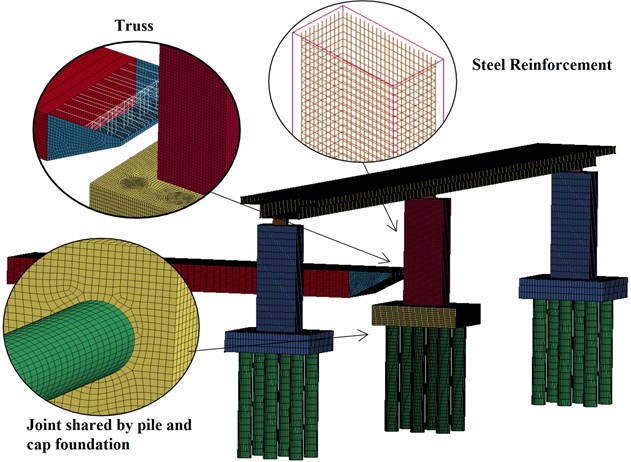
For the barge structure, SHELL163 and BEAM161 elements are adopted respectively to simulate the outer plate of the bow and the bow internal trusses, and the barge body adopts SOLID164 element. The bridge deck adopts SHELL163 element, and the steel reinforcement adopts BEAM161 element, while the rest of the bridge adopts SOLID164 element. In order to improve the calculation accuracy, the mesh of the bow structure and the pier involved in the collision is refined; the size is set to 200 mm. Therefore, the barge-whole bridge finite element model is divided into 247419 elements, including 42107 elements for the barge and 205312 elements for the whole bridge. The finite element model of barge impacting the whole bridge is shown in Fig. 2.

Fig. 2The barge-whole bridge finite element model

2.2. Material model and contact

The barge body hardly gets involved in collision. So, it is set as a rigid body and the material model is *MAT_RAGID. The material of barge bow and steel reinforcement adopt the Plastic Kinematic Model. Its parameters are density $\rho =$7.89×10^-6 kg/(mm)³, elastic modulus $E=$207 GPa, Poisson’s ratio $\nu =$0.28, yield strength ${\sigma }_Y$ = 235 MPa, failure strain ${\epsilon }_f$ = 0.35, $C=$20 and $P=$5, respectively. Linear elastic material *MAT_ELASTIC is selected for structures which are not directly involved in collision, such as bridge deck, side pier, laminated rubber bearing, pile foundation. The pier material model involved in ship-bridge collision adopts the HJC concrete constitutive model. The relevant material parameters of the model are shown in Table 1.

To simulate concrete damage in actual collision, this paper adds concrete failure criterion based on the HJC concrete constitutive model [11]-[12]. The maximum pressure of 35 MPa as well as the maximum principal strain of 0.02 is set as the failure criterion of concrete for joint judgment to obtain better damage effects. There is no solid physical foundation for the setting of failure criteria, but better impact dynamic response results can be obtained.

It is very important to define the ship-pier contact correctly for collision numerical simulation [13]. In the meshing phase of the bridge, the common nodes are used to connect the pile foundation with the pile cap, pile cap with the pier column, and pier column with the laminated rubber bearing. This method reduces the contact setting. Consequently, two contact types are set up in this paper. The keyword of the contact type between bow and pier in LSDYNA is *CONTACT_AUTOMATIC_SURFACE_TO_SURFACE. And the bow is defined as Contact Surface, while the pier is defined as Target Surface. The contact type between the bow internal trusses and outer plate in LSDYNA is *CONTACT_AUTOMATIC_SINGLE_SURFACE. The coefficients of kinetic and static friction for both contact types are set to 0.3.

3.1. Analysis of system energy and impact force

As shown in Fig. 3 and Fig. 4, the barge-bridge collision process is energy conservation. The collision between the barge and the whole bridge occurred in 0.25s. At this moment, the kinetic energy of the barge quickly began to be converted into the internal energy of the system until the barge and the bridge were separated. In the process of numerical simulation of collision, the hourglass energy should be less than 5 % of the total energy, otherwise the numerical results are invalid [14]. In this paper, the maximum hourglass energy is 3.549×10⁵ J, accounting for only 2.8 % of the initial kinetic energy, and the maximum sliding energy and damping energy are 1.618×10⁵ J and 3.190×10⁵ J respectively, accounting for 1.3 % and 2.5 % of the initial kinetic energy, which proves the effectiveness of the numerical simulation results.

Fig. 3Time-history curve of system energy

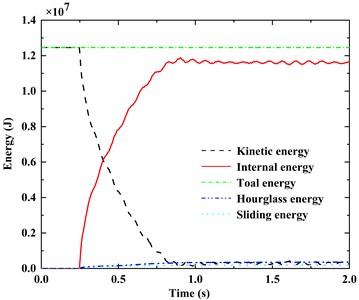
Fig. 4Percentage of kinetic energy

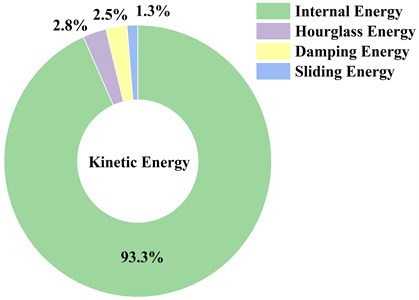
Fig. 5Time-history curve of impact force

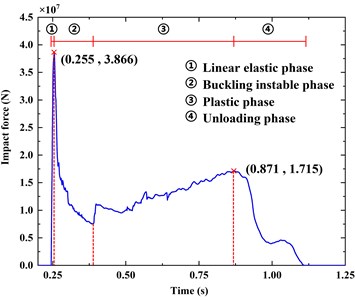
As shown in Fig. 5, the trend of impact force curve corresponds to the four phases of barge bow in the collision process, which are: (1) Linear elastic phase, where impact force reaches the maximum value of 38.659 MN; (2) Buckling unstable phase, where impact force drops rapidly; (3) Plastic deformation phase, where impact force increases non-linearly; (4) Unloading phase, where impact force drops to 0 at 1.105 s.

It is worth noting that during the plastic phase, the impact force is not a simple monotonic increase and decrease process, but shows the characteristics of alternation and fluctuation. This is because the shell elements of the barge bow involved in the collision yield during the collision, resulting in the temporary separation of the bow and the pier. Then, as the barge continues to move forward, the shell elements contact the pier again, and this process reciprocates alternately.

3.2. Dynamic behavior analysis of Bridges

The stress nephogram of the bridge is shown in Fig. 6. Stress concentration occurred in the area where the pier was impacted (region 1), the connection between the pile foundation and the pile cap (region 2), the restraint of the pile foundation (region 3) and the contact between the pier and the bridge deck (region 4). The region 4 and the impacted side of region 3 and region 2 are the principal tensile stress, which is easy to produce concrete cracking. Moreover, the region 2 and the opposite side of area 1 are the principal compressive stress, which is easy to produce large plastic deformation. In the process of barge-bridge collision, the damage of pier is mainly concentrated in these four regions, and the protection of these four regions should be emphatically considered in the design of anti-collision facilities.

Fig. 6Nephogram of bridge concrete stress

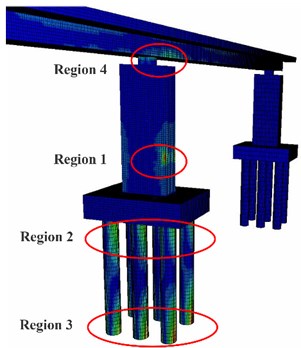
a) Bridge

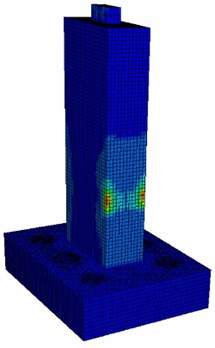
b) Pier

c) Pile foundation

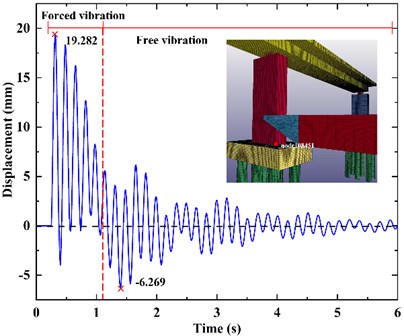
Select the node 108514 at the top of the bridge pier and extract its transverse displacement, as shown in the Fig. 7. The maximum top displacement of the impacted pier is 17.739 mm, but its peak time lags behind the time when the impact force reaches the maximum value. Fig. 7 shows that the displacement of bridge is divided into two phases. The first phase is the forced vibration phase. The barge impacts the bridge at 0.25 s and forces the bridge to move along the forward direction of the barge until the impact force is 0 at 1.105 s, then the collision ends. The second phase is the free vibration phase. Due to inertia, the pier moves towards the forward direction of the barge for a period of time, and then starts to vibrate freely, and the displacement decays with time.

Fig. 8 shows the transverse displacement of the node 108451 at bottom of the bridge pier, with the maximum displacement of 19.282 mm. It can be seen from Fig. 8 and Fig. 8 that the displacement at the top of the pier is rougher than that at the bottom of the pier. This is because the pier is damaged by barge impact, and the pier element becomes a dead element, which affects the displacement of the bridge. The roughness of the displacement curve represents the damage of the pier structure.

Fig. 7The displacement at the top of pier

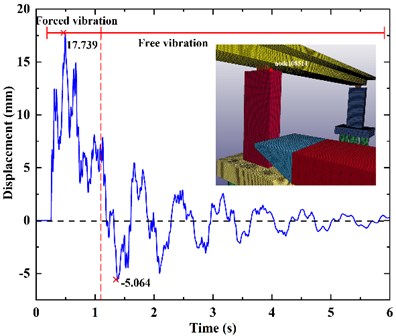
Fig. 8The displacement at the bottom of pier

3.3. Analysis of structural damage

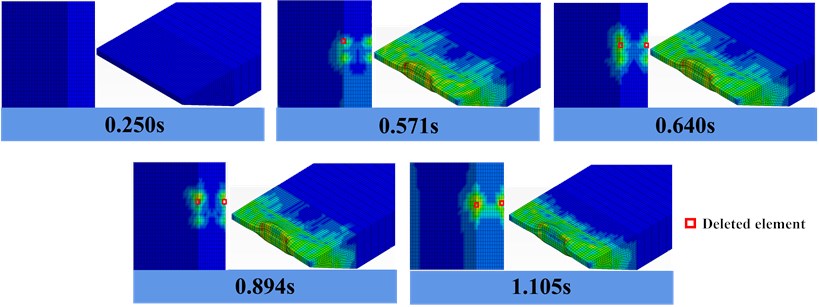
According to the von Mises stress nephogram in Fig. 9, the ship and bridge began to contact in 0.25 s, and a high stress concentration appeared at the edge of the square pier. When the collision time reached 0.571 s, the pier concrete reached the prescribed failure values, and the concrete elements were deleted. As the collision continued, the concrete damage became more and more serious until the end of the collision at 1.105 s. Meanwhile, the barge bow is constantly loaded and unloaded during the collision, resulting in serious plastic deformation. The deformation is mainly concentrated in the contact area between the barge bow and the pier. There is no shell element deletion.

Fig. 9Barge-whole bridge stress nephogram, Left concrete bridge, right barge

4.1. Influence of barge impact velocity

To change the barge impact velocity, we set three working conditions as follows: 2 m/s, 3 m/s and 4 m/s. The time history curve of impact force under different barge impact velocities is obtained.

As shown in Fig. 10, with the increase of impact velocity, the peak impact force increases, the duration of the ship-bridge collision also increases and the curve presents more significant non-linear characteristics. The non-linearity of the curve indicates the damage and failure of the structure.

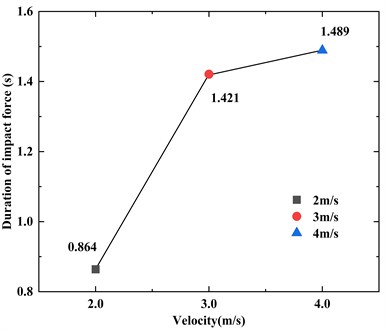
In Fig. 11 and Fig. 12, There is a clear linear relationship between the peak impact force and the impact velocity and the duration of impact force is irregular with the increase of the velocity.

Fig. 10Time-history curves of impact force under different impact velocities

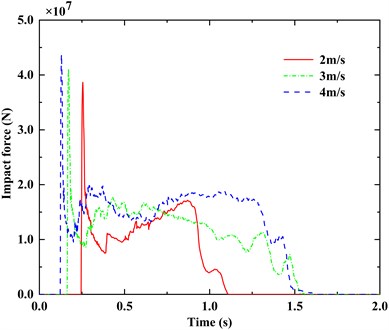
Fig. 11Peak impact force at different impact velocities

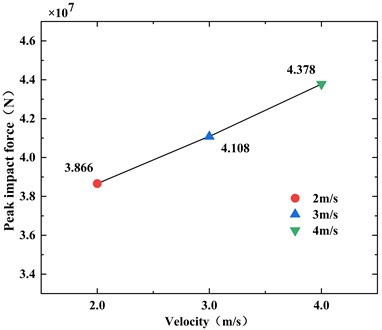
Fig. 12Duration of impact force at different impact velocities

4.2. Influence of barge mass

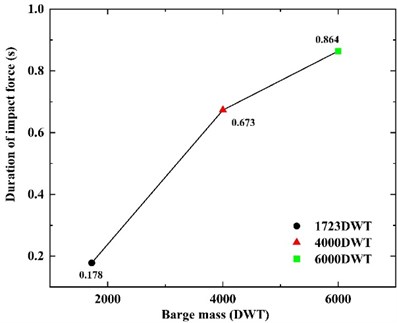
To change the barge mass, we set three working conditions, namely 1723DWT, 4000DWT and 6000DWT. 1723DWT means the barge is empty and 6000DWT is full.

As shown in Fig. 13 and Fig. 14, The increase of barge mass changes the initial kinetic energy of the barge. The increase of kinetic energy leads to the increase of internal energy converted by collision, which in turn affects the response characteristics such as impact force. With the increase of barge mass, the fluctuation of the time history curve of impact force increases obviously. This indicates that the buckling damage of barge bow is becoming serious.

According to Fig. 15 and Fig. 16, there is a linear relationship between the barge mass and the peak impact force, but the values between the peak impact force exist barely variation. The value of 1723DWT is merely 0.524 MN smaller than 6000DWT. However, the duration of impact force changes obviously. The impact duration of 6000DWT barge is about 4.85 times that of 1723DWT. Longer contact time leads to more complex nonlinear response.

Fig. 13Conversion of kinetic energy and internal energy

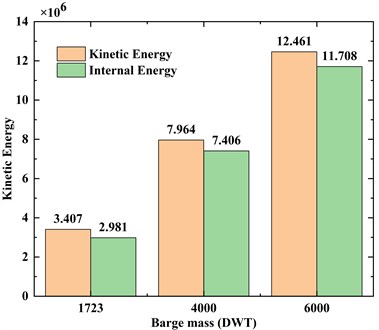
Fig. 14Time-history curve of impact force under different barge mass

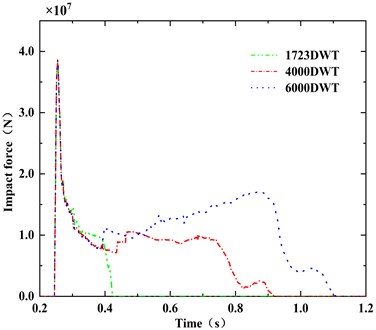
Fig. 15Peak impact force at different barge mass

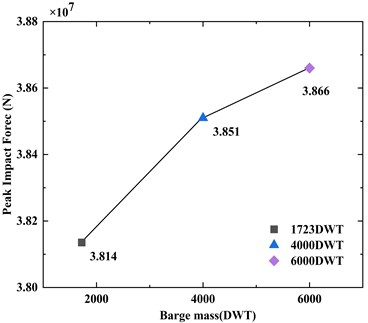
Fig. 16Duration of impact force at different barge mass