Experimental investigation of kinematic characteristics of a wheeled vibration-driven robot

2.1. General design of the wheeled vibro-impact robot developed in SolidWorks software

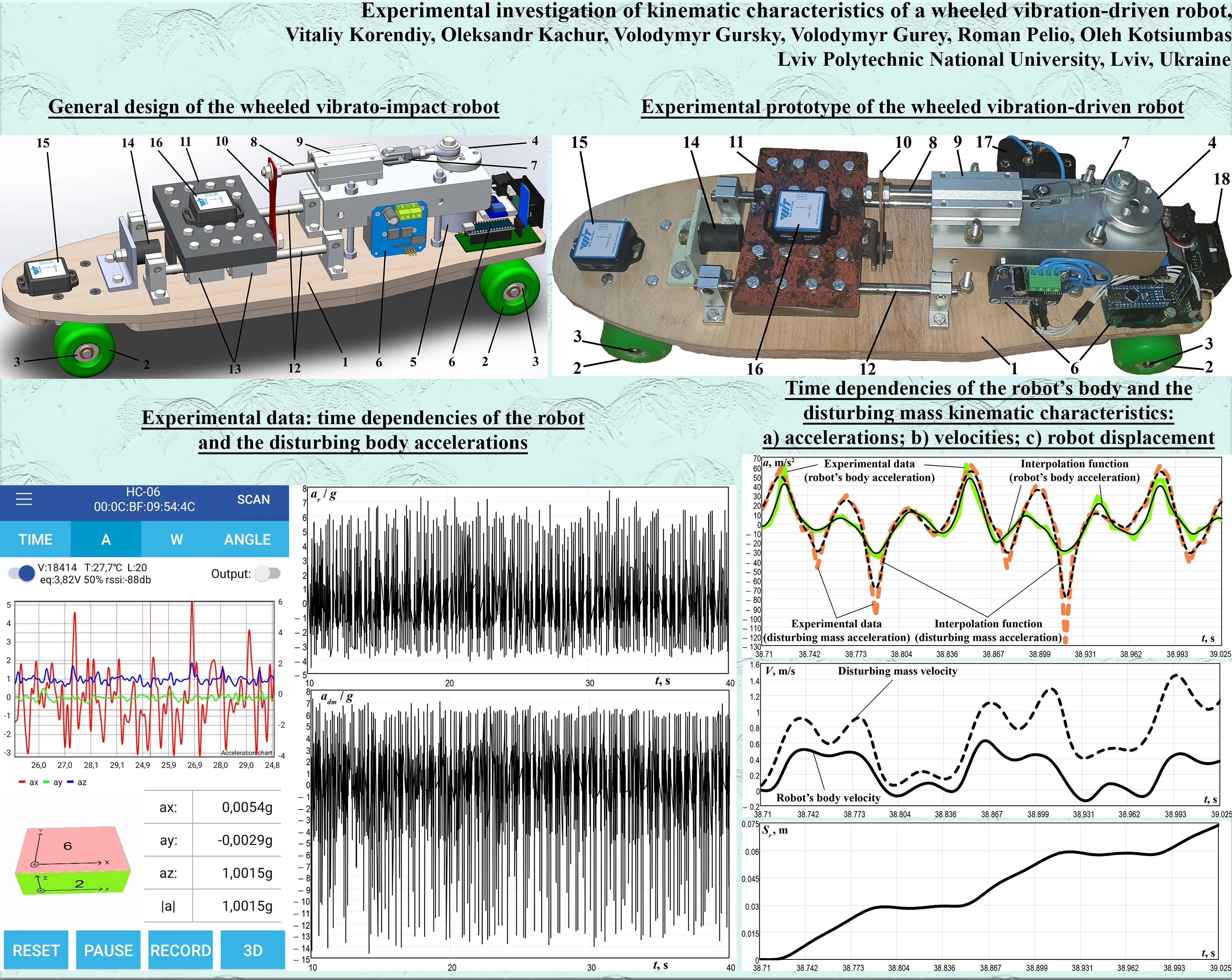
The 3D-model of the wheeled vibration-driven robot was designed in the SolidWorks software (see Fig. 1). The robot’s body 1 is based on the wheeled supports 2. The wheels are allowed to rotate counterclockwise due to applying the roller-type overrunning (free-wheel) clutches 3 that engage in one direction and free-wheel in the other one. The eccentric (crank) 4 is driven by the DC motor 5 controlled by the electronic system 6. With the help of the connecting rod 7, the rotation of the eccentric 4 is transformed to the translational motion of the slider (sliding rod) 8 supported by the linear (guide, pilot) bearing 9. The latter is fixed on the robot’s body 1. The slider 8 is connected to the flat spring 10 actuating the impact (disturbing) body 11. The latter can slide along the guides (guide rods) 12 due to the application of the linear bearings 13. The translational oscillations of the impact body 11 cause the displacements of the robot’s body mass center, and generate the forward step-wise motion of the wheeled platform 1 restricted from the backward motion by the overrunning (free-wheel) clutches 3. In order to increase the robot locomotion speed and improve its operational efficiency, it is proposed to use the vibro-impact working regimes. The latter take place when the disturbing body 11 periodically impacts the rubber damper 14 connected to the wheeled platform 1. In order to carry out experimental investigations on the robot dynamic behavior, the accelerometers 15 and 16 are fixed to the robot’s body and to the disturbing body, respectively.

Fig. 1General design of the wheeled vibrato-impact robot

2.2. Engineering prototype of the robot and experimental technique

The experimental prototype of the wheeled vibro-impact robot (Fig. 2) has been developed at the Vibroengineering laboratory of Lviv Polytechnic National University. All the position numbers referenced in Fig. 2 correspond to the ones used in the 3D-model (Fig. 1). The experimental prototype is additionally equipped with the constant-voltage source 17 (of the nominal value equal to 15 V), and the voltmeter 18. All the control functions are performed remotely from the mobile phone using the Bluetooth technology. The control system 6 is based on the Arduino hardware and software. The Bluetooth sensors WT901BLECL manufactured by the WitMotion company (see positions 15 and 16 in Fig. 2) allow for simultaneous measuring of the robot and the impact body accelerations at the retrieval rate of 200 Hz and the bandwidth up to 256 Hz. The driving DC motor equipped with the planetary-type gearbox provides the controllable rotation frequency of the eccentric 4 in the range of 0,…, 1000 rpm (0,…, 16.7 Hz). The mass of the whole robot is equal to 3.8 kg, and of the impact body – 1.6 kg.

Fig. 2Experimental prototype of the wheeled vibration-driven robot

The experimental technique consists of two basic stages: studying the motion conditions and making the corresponding measurements; analyzing the obtained results and forming the conclusions. In the first stage, the robot is set into motion at a certain forced frequency controlled by the voltage value applied to the DC motor. The accelerometers’ data is written by the WitMotion application and stored in the memory of the mobile phone. The obtained results are presented in the form of time dependencies of the corresponding accelerations relative to the free-fall (gravity) acceleration $g$. Therefore, the absolute values of these accelerations can be easily calculated. Then, using the MathCad software, the numerical integration of the obtained results is to be performed in order to obtain the time response curves of the robot and the disturbing mass velocities and displacements. The mentioned experimental investigations can be carried out several times for different values of the forced frequency, disturbing mass, spring stiffness, impact gap, and eccentricity of the crank-type vibration exciter.

3.1. Experimental results

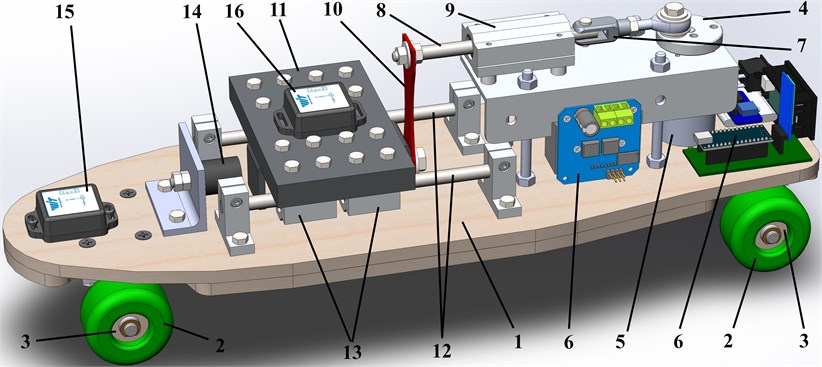
The experimental data has been recorded by the WitMotion application (see Fig. 3) and transformed into the numerical format in the form of the Excel table. The sensor retrieval rate is about 200 Hz; therefore, the time interval of the measured data is approximately 0.005 s. The experimentally obtained time dependencies of the robot’s body $a_r$ and the disturbing mass $a_{db}$ accelerations are presented in Fig. 3. The maximal values of the wheeled platform acceleration reach 7$g$ (68.7 m/s²), while its deceleration doesn’t exceed 4$g$ (39.2 m/s²). The mentioned parameters of the disturbing mass are equal to 7$g$ (68.7 m/s²) and 14$g$ (137.3 m/s²), respectively. The periodical peaks of the robot’s body and the impact mass accelerations are observed at the same time moments and correspond to the forced frequency of about 8 Hz. This allows for drawing a preliminary conclusion about the vibro-impact motion conditions.

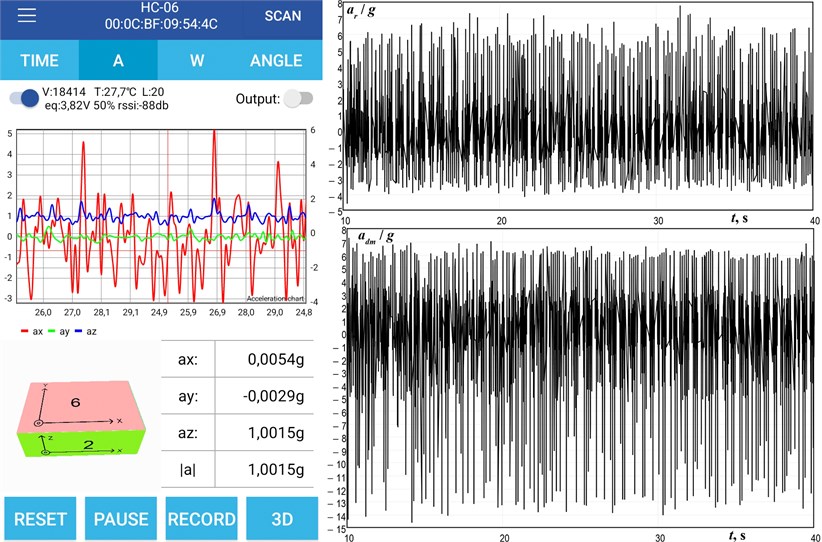
The obtained experimental results have been thoroughly analyzed, and the entire time interval of the carried-out measurements has been divided into several subintervals. The latter take into account the stable indications of the measuring equipment characterized by the constant time steps of 0.005 s. One of such intervals takes place within 38.710,…, 39.025 s (Fig. 4). The numerical interpolation algorithms integrated in the MathCad software allow for quick processing of the discrete experimental data, and generating the continuous (polynomial) acceleration functions with the prescribed accuracy. The examples of such functions are plotted in Fig. 4(a), where the green and orange curves present the experimental data obtained from the robot’s body and the disturbing mass accelerometers (positions 15 and 16 in Fig. 1), and the corresponding black curves interpolate this data in the form of the polynomial function.

Fig. 3Experimental data: time dependencies of the robot and the disturbing body accelerations

3.2. Analyzing the robot kinematic characteristics

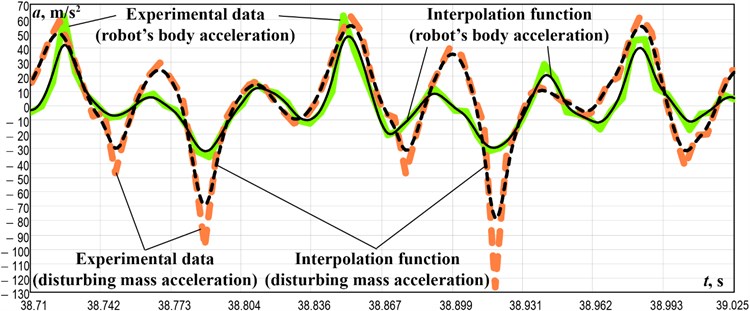
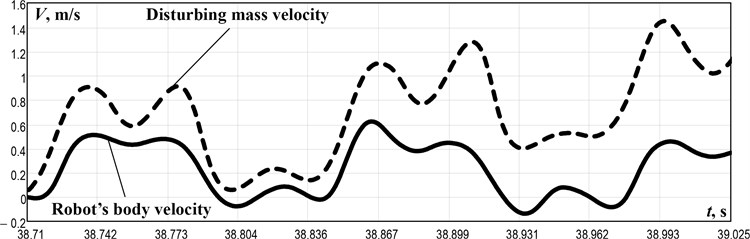
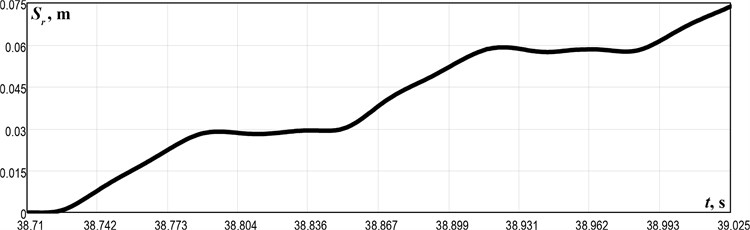
In order to analyze the other kinematic characteristics of the robot’s body motion, it is necessary to perform the numerical integration of the obtained experimental data of the wheeled platform acceleration using the applied software, particularly PTC MathCad. The corresponding results presenting the time dependencies of the robot velocities and displacements are shown in Fig. 4. The robot’s body velocity periodically reaches its maximal values of about 0.6 m/s, while its minimal values fall to –0.1 m/s (Fig. 4 (b)). The disturbing mass velocity periodically changes in the range of 0,…, 1.4 m/s. The general character of the robot motion corresponds to the one previously modeled and simulated in the papers [14] and [15]. The wheeled platform performs the step-wise motion and travels a distance of about 74 mm during the time interval of 0.315 s (within 38.710,…, 39.025 s). Single-step duration is about 0.12,…, 0.13 s, and the distance traveled by the robot during one step is almost 0.03 m (Fig. 4(c)). Therefore, it can be concluded that the robot average speed is approximately 0.23 m/s. The same results can be obtained when analyzing the interpolated time dependencies of the robot velocity in the MathCad software using the following “averaging” formula:

where $V_{r\_aver}$ is the average value of the robot’s wheeled platform velocity; $f_{for}$ is the forced frequency provided by the controllable driving motor shaft rotation ($f_{for}$ ≈ 8 Hz); $t_0$ denotes the starting moment of time for carrying out the numerical calculations; $V_{r.}\left(t\right)$ is the continuous function of the robot’s body velocity numerically integrated in the MathCad software using the interpolated polynomial function of the robot acceleration (see Fig. 4(a) and (b)).

Fig. 4Time dependencies of the robot’s body and the disturbing mass kinematic characteristics: a) accelerations; b) velocities; c) wheeled platform displacement

a)

b)

c)