Abstract
Appropriate vibration parameters can improve the efficiency of vibration harvesting, so the selection of vibration harvesting parameters is very important. In this paper, the stress of olive fruit is analyzed, and the vibration of olive tree is tested and simulated. Design-Expert 12.0 is used for experimental design, The diameter, height and angle of main branches were selected as the test factors, and the optimal vibration frequency and force were selected as the evaluation indexes. determines the optimal vibration frequency through modal analysis; the optimum vibration force is determined by harmonic response analysis and test. The quadratic polynomial response regression model of optimal vibration frequency and optimal vibration force is obtained. The research results can provide reference for the design of Vibrating harvester.
Highlights
- Through the stress analysis and experiment of fruit, the average abscission acceleration of fruit was obtained.
- The relationship between simulation and experiment is obtained.
- A method of obtaining vibration harvesting parameters through simulation is introduced.
- The relationship between the morphological parameters of olive and vibration harvest parameters was obtained through the simulation test.
1. Introduction
Olive oil is an oil crop of Oleaceae oleander. Harvesting accounts for a large proportion in the production cycle of olive. According to statistics, in the traditional manual harvesting, the labor cost of harvesting accounts for up to 35 %-45 % of all labor costs [1], while mechanized harvesting can improve the efficiency of harvesting and promote the development of olive industry. In mechanized recovery, reasonable parameters can greatly improve recovery efficiency [2]. Therefore, it is necessary to study the parameters of vibration recovery.
Mechanized harvesting of fruits by vibration is one of the effective means to improve the productivity of the whole fruit trees. Therefore, many scholars have studied the vibration parameters and harvest effect of fruit harvest. In 2015, Leone et al. Conducted vibration experiments on different varieties of olive trees with the same tree age, and obtained the best vibration harvesting frequency and time of different varieties of olive trees [3]. Moreover, San et al. analyzed the response state of apricot trees under different vibration excitation, and obtained the optimal vibration harvesting frequency of apricot trees [4]. Hu et al. Simulated and tested the apple harvesting process of comb brush harvester, and explored the effects of seven different factors on apple stress in the harvesting process, the results showed that three parameters were directly related to apple stress in 2020 [5]. In 2021, Zhao et al. Studied the effects of speed, material and amplitude on the recovery of Lycium barbarum through simulation and experiment [6].
In the above studies, most researchers focused on the differences of vibration parameters between different varieties of fruit trees, at present, there is no researchers have paid attention to the differences of vibration parameters between fruit trees of the same variety. Therefore, this paper will study the vibration harvesting parameters of three open-center shape olive trees with different parameters through finite element simulation and experiment.
2. Materials and methods
2.1. Force analysis and Fruit-stalk separation conditions
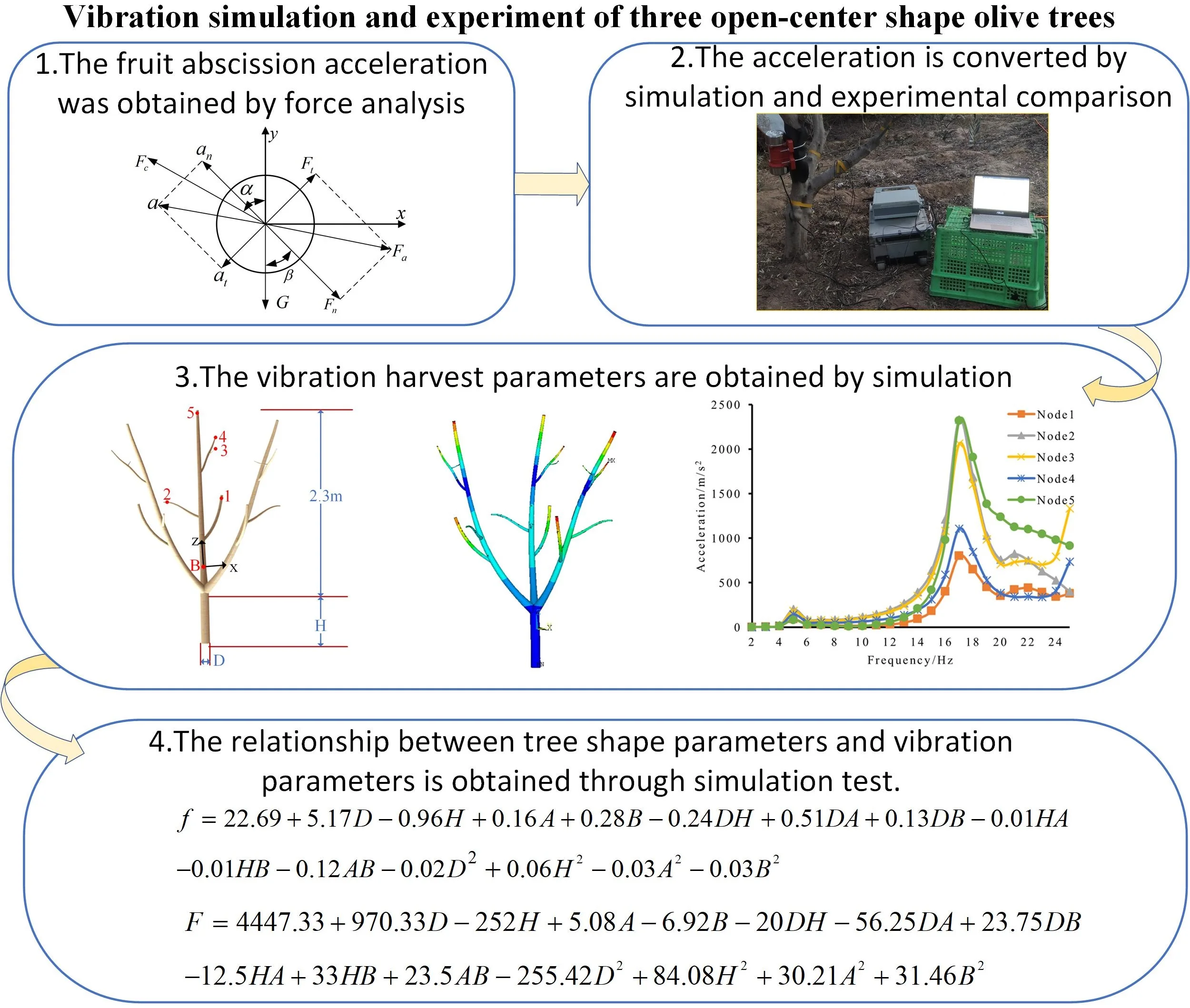
The general eccentric block harvester is of single eccentric block type. The single eccentric block generates a constant centrifugal force under rotation to form circumferential excitation, It can be decomposed into component forces with equal size, phase difference of 90 degrees and located in X and Y directions respectively, as shown in Fig. 1, and the mechanical model is shown in Eq. (1):
where m is the mass of eccentric block, e is the eccentricity, ω is the rotational angular velocity, t is the time, Fx is the component force in the x-axis direction, and Fy is the component force in the y-axis direction.
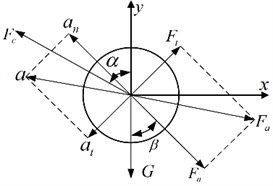
The plane stress diagram of olive fruit is shown in Fig. 2, and the fruit abscission condition is shown in Eq. (2). Ignoring the difference between α and β and the influence of gravity [7], it can be reduced to Eq. (3):
where Fc is the binding force between the fruit and the fruit stalk, a is the fruit acceleration, an and at are components of acceleration, Fa is the inertial force generated by the vibration of the fruit, Fn and Ft are components of inertial force.
Through experimental measurement, the average weight of olive fruit at maturity was 4.1 g, and the average binding force between fruit and fruit stalk was 3.73 N. Therefore, the average abscission acceleration of olive fruit is 909.76 m/s2.
Fig. 1Schematic diagram of single eccentric block excitation:
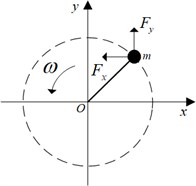
Fig. 2Stress analysis diagram of olive fruit
2.2. Simulation experiment design
The pruned olive tree is a three open-center shape tree. Assuming that the main branches of olive tree are located in the plane perpendicular to the ground, the three main branches are the same, and the branch section is circular, the three-dimensional model of olive tree is established through the lofting function in SolidWorks, as shown in Fig. 3. According to the actual measurement and observation, there are differences in trunk thickness, height and included angle between main branches of different olive trees. Therefore, the trunk diameter D, trunk height H and main branch angle A and B are selected as the test factors, in which the ratio between the cross sections of each branch of olive tree and the trunk diameter is constant, the optimal vibration frequency and exciting force are selected as the evaluation indexes, and the four factor three-level experiment is designed by using Design-Expert 12.0.3 software, and a total of 27 groups of experiments were carried out. The horizontal code table is shown in Table 1.
Fig. 3Three dimensional model of olive tree
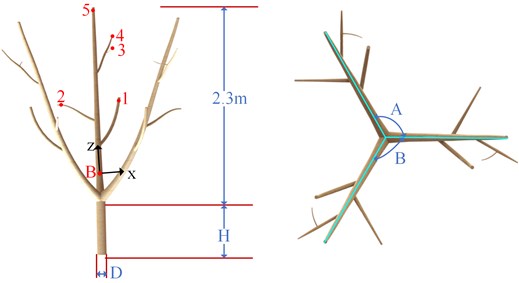
Table 1Coding table of test factors
Code | Factor | |||
D / mm | H / mm | A / ° | B / ° | |
–1 | 100 | 500 | 100 | 100 |
0 | 130 | 600 | 125 | 125 |
1 | 160 | 700 | 150 | 150 |
2.3. Vibration test and simulation
In order to verify the correlation between the simulation and the actual process, a olive tree in an olive garden was randomly selected for vibration test, The trunk diameter D is 153 mm; The height h of the trunk is 510 mm; The included angles of main branches a and B are 125° and 130° respectively. The vibration motor with adjustable speed is used to provide vibration force, and the vibration motor is fixed with U-bolts, the selected frequency and corresponding excitation force are shown in Table 2. The selected excitation point is point B in Fig. 4(b), and the position of acceleration measurement point is shown in Fig. 4(b). At the same time, the harmonic response analysis consistent with the test conditions is carried out. The established 3D model is imported into ANSYS 19.0 for simulation analysis. The density of olive tree is1024 kg/m3, and the stiffness matrix is shown in Eq. (4):
The damping ratio is 0.04. Apply fixed constraints to the bottom of the tree.
Table 2Force magnitude and frequency during simulation and test
Frequency / Hz | 10 | 15 | 20 | 25 | 30 |
Force / N | 30 | 70 | 120 | 190 | 270 |
2.4. Simulation
Modal analysis can be used to determine the inherent properties of olive trees, so modal analysis is used to determine the optimal vibration frequency. The first 20 modes of olive tree are selected for natural frequency analysis.
The steps to determine the optimal vibration force are as follows: firstly, apply the excitation force with the size of 1000 N and the phase difference of 90 ° to the X and Y directions of point B in Fig. 3 respectively, and the acceleration of the endpoint (Fig. 3) of the branch is obtained by simulation. According to the linear nature of harmonic response analysis [8], amplify the acceleration to the acceleration required for fruit abscission, obtain the corresponding vibration force, set it as the simulated vibration force, and the simulated vibration force is applied to point B for verification.
Fig. 4The test of measuring acceleration

a) Testal setup
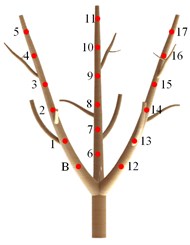
b) Distribution of measuring points
3. Results and analysis
3.1. Analysis of vibration test and simulation results
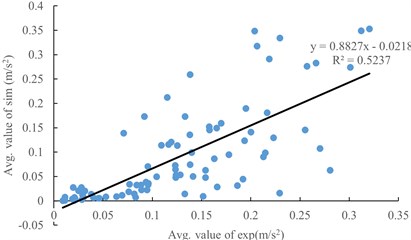
The synthetic accelerations of different points on the branch are obtained through simulation and test. The correlation coefficient between simulated acceleration and simulated acceleration is calculated by SPSS v26.0, which is 0.724, which proves that there is a great correlation between test and simulation. The simulated acceleration is linearly fitted with the simulated acceleration, and the results are shown in Fig. 5. The average abscission acceleration (909.76 m/s2) of olive fruit was substituted into the fitting curve, and the abscission acceleration in the simulation was 803.02 m/s2.
Fig. 5Comparison between test and simulation
3.2. Modal analysis
According to the results of modal analysis, the modes of olive are divided into three categories, as shown in Fig. 6. At the intermediate frequency, the vibration displacement is the largest and the whole olive tree is vibrating, which is conducive to vibration harvesting [9]. Therefore, this frequency is taken as the optimal vibration frequency.
Fig. 6Modal analysis results
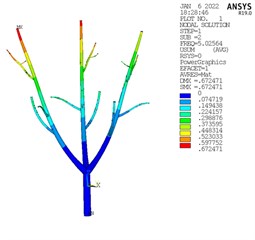
a) Lower frequency
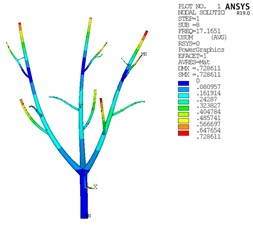
b) Intermediate frequency
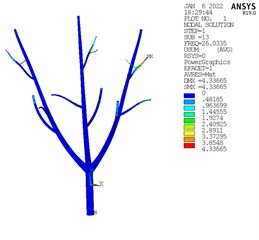
c) Higher frequency
3.3. Harmonic response analysis
According to the steps of determining the optimal vibration force in Section 2.4, the excitation force with the size of 1000 N and the phase difference of 90° is applied to the X and Y directions at point B respectively. The acceleration frequency curve of the olive branch endpoint in Fig. 3 can be obtained, as shown in Fig. 7(a), the peak value corresponding to 17 Hz is the largest, and the acceleration of point 1 at 17 Hz is the smallest, which is 246.8 m/s2. According to the linear nature of harmonic response analysis, the acceleration is proportionally amplified to 803.02 m/s2. At this time, the applied simulated excitation force should be 3255 N. When a circumferential excitation force of 3255 N is applied at point B, the acceleration frequency curve of the corresponding point is shown in Fig. 7(b). Compared with Fig. 7(a), the linear nature of harmonic response analysis is verified.
Fig. 7Harmonic response analysis results
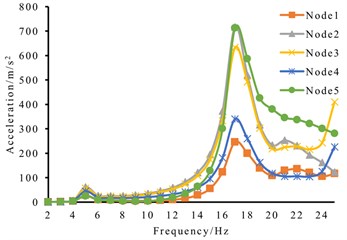
a)
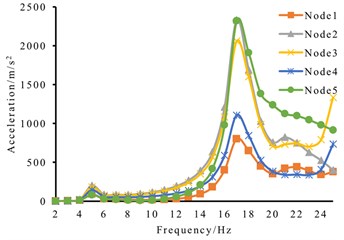
b)
3.4. Analysis of simulation experiment results
27 groups of simulation experiments were carried out, and the analysis of variance was carried out. The results show that the p value of the two models is less than 0.05 and the values of lack of fit were more than 0.1, so the regression model is significant. The quadratic polynomial response regression models of the optimal vibration frequency (f) and the optimal vibration force(F) are established respectively, the coding equation is shown in Eqs. (5-6):
4. Conclusions
In order to study the difference of vibration harvesting parameters of olive trees with the same tree shape, this paper uses the method of finite element simulation and tests. The main conclusions of this study are as follows:
The stress analysis and experiment of olive fruit showed that the average abscission acceleration of fruit was 909.76 m/s2. The vibration of olive tree is tested by vibration motor, and the comprehensive acceleration of test and simulation is analyzed. The results show that there is a good correlation between the test and simulation results, and the simulation and experimental acceleration are fitted. Through the fitting results, the fruit abscission acceleration is converted to the simulation acceleration, which is 803.02 m/s2.
The modal analysis of olive tree shows that the medium frequency is the best vibration frequency. The harmonic response of the acceleration at the end of the olive branch is analyzed, and the simulated vibration force is obtained according to its linear characteristics.
Through the four factor and three-level experiment designed by Design-Experts, the experimental data are analyzed. The results show that the model has good significance, and a quadratic polynomial response regression model with vibration frequency and vibration force as evaluation indexes is established.
References
-
K. F. Sanders, “Orange harvesting systems review,” Biosystems Engineering, Vol. 90, No. 2, pp. 115–125, Feb. 2005, https://doi.org/10.1016/j.biosystemseng.2004.10.006
-
Y. Qian et al., “Dynamic simulation analysis and modal experiment of Camellia oleifera tree,” in 2020 ASABE Annual International Virtual Meeting, July 13-15, 2020, pp. 1–8, 2020, https://doi.org/10.13031/aim.202000076
-
Leone A., Romaniello R., Tamborrino A., Catalano P., and Peri G., “Identification of vibration frequency, acceleration, and duration for efficient olive harvesting using a trunk shaker,” Transactions of the ASABE, Vol. 58, No. 1, pp. 19–26, Feb. 2015, https://doi.org/10.13031/trans.58.10608
-
San Y., Yang H., Wang X., Niu C., Guo W., and Hou S., “Effects of vibration mode and frequency on vibration harvesting of apricot trees,” (in Chinese), Transactions of the Chinese Society of Agricultural Engineering, Vol. 34, No. 8, pp. 10–17, 2018.
-
G. Hu, L. Bu, and J. Chen, “Simulation to determination of significant parameters on apple stress for combing harvesting in trellis trained trees,” Scientia Horticulturae, Vol. 274, p. 109654, Dec. 2020, https://doi.org/10.1016/j.scienta.2020.109654
-
J. Zhao et al., “Parameter optimization of vibrating and comb-brushing harvesting of Lycium Barbarum L. Based on FEM and RSM,” Horticulturae, Vol. 7, No. 9, p. 286, Sep. 2021, https://doi.org/10.3390/horticulturae7090286
-
Wu D., Zhao E., Jiang S., Ding D., Liu Y., and Liu L., “Optimization analysis and test of canopy vibration parameters of camellia fruit based on double pendulum model,” (in Chinese), Transactions of the Chinese Society for Agricultural Machinery, Vol. 52, No. 12, pp. 96–104, 2021.
-
L. Fu, J. Peng, Q. Nan, D. He, Y. Yang, and Y. Cui, “Simulation of vibration harvesting mechanism for sea buckthorn,” Engineering in Agriculture, Environment and Food, Vol. 9, No. 1, pp. 101–108, Jan. 2016, https://doi.org/10.1016/j.eaef.2015.08.003
-
H. Bentaher, M. Haddar, T. Fakhfakh, and A. Mâalej, “Finite elements modeling of olive tree mechanical harvesting using different shakers,” Trees, Vol. 27, No. 6, pp. 1537–1545, Dec. 2013, https://doi.org/10.1007/s00468-013-0902-0
About this article
This research was supported by the National Key research and development Plan of China (Grant No. 2019YFD1002401).
