Seismic researches on a new assembled monolithic RC structure based on IDA

1. Introduction

Advantages of assembled monolithic concrete structure include fewer energy consume, controllable quality, quicker construction speed, better constructional spot environment and fewer shrinkage cracks. Wide attention was paid to this kind of structure in recent years worldwide. However, compared with traditional cast-in-place concrete structure, there exist some disadvantages of assembled monolithic concrete structure, such as poorer integrity and seismic behaviors [1-3]. Therefore, experts worldwide have done lots of researches to improve seismic behaviors of assembled monolithic concrete structure.

For example, Jianqiang [4] Han studied seismic behaviors of unbonded prestressed assembled frame structure; Wan G. [5] studied seismic behaviors of precast concrete partition wall by method of Pushover analysis based on displacement, and Biswal A. [6] studied influences on shear behaviors of precast concrete board wall with different vertical joints.

This article is based on former studies [7-9], and a new assembled monolithic concrete structure is therefore established. According to seismic design theory in the current Chinese seismic design code [10], seismic behaviors of the assembled monolithic concrete structure are studied by method of incremental dynamic analysis (IDA), which are expected to obtain relevant conclusions so that decision-makers and designers of engineering construction can have more choices.

2. Calculation model

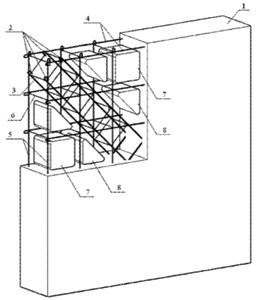
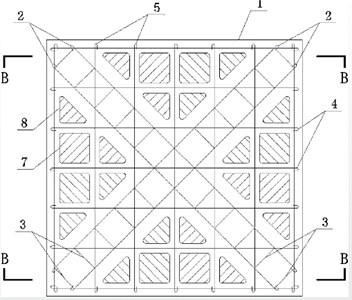
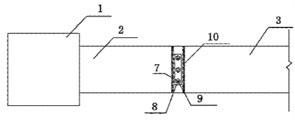
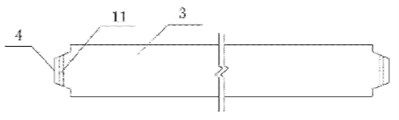
New components of a new light assembled monolithic structure are developed as shown in Fig. 1 and Fig. 2.

The calculation model is based on a real engineering in Henan. The basic information of the engineering are as follows. Design working life is 50 years, and earthquake fortification intensity is VI. Basic seismic acceleration is 0.05 g, and classification of design earthquake is the first group. Site classification is class II, and aseismic grade is the third one. Basic wind pressure is 0.35 k N/m², and terrain roughness is B class. The above introduced assembled components are adopted at walls and some beam-column joints.

Fig. 1Diagram of an assembled hollow shear wall component with slant-cross reinforcement: 1 – concrete wall; 2 – slant-cross longitudinal reinforcement; 3 – stirrups of slant-cross longitudinal reinforcement; 4 –reinforcements of the wall in horizontal direction; 5 – reinforcements of the wall in vertical direction; 6 – normal reinforcements; 7 – internal blocky foamed plastic model; 8-expanded polystyrene foamed plastic

a)

b)

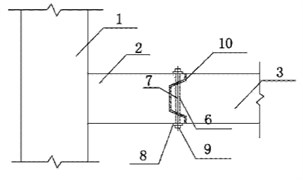
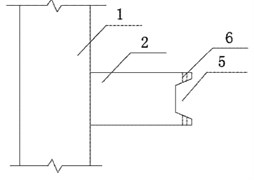
Fig. 2Diagram of assembled frame beam column with vertical joints: 1 – precast column; 2 – bracket; 3 – precast beam; 4 – Protrusion; 5 – groove; 6 – bracket bolt hole; 7 – bolt; 8 – bolt backing plate; 9 – nut; 10 – bonding layer; 11 – bolt hold of precast beam)

a)

b)

c)

d)

Fig. 3Stress-strain curve of concrete

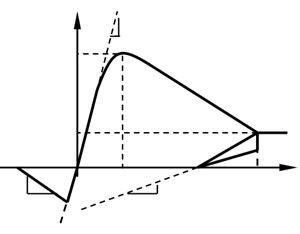
Fig. 4Stress-strain curve of steel

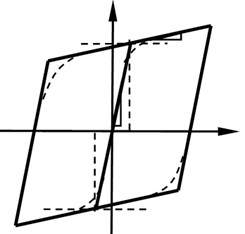
Wall components, beams, columns and bracings of the new assembled monolithic structure are simulated by using fiber elements of nonlinear BeamColumn in OpenSees software. Uniaxial Material Concrete02 in OpenSees software is used as concrete constitutive relation, and the constitutive relation model is shown in Fig. 3. Uniaxial Material Steel02, a bilinear kinematic hardening model, in OpenSees software is used as constitutive relation of both steel bar and steel pipe adopted by steel pipe concrete, and the constitutive relation model is shown in Fig. 4.

The finite element calculation model of assembled monolithic structure system is constructed by using Opensees finite element software.

3. IDA method

Incremental dynamic analysis is based on nonlinear time-history analysis. By calculating massive earthquake responses, it can analyze seismic behaviors of a building structure. This method takes many factors into consideration, such as different seismic requests of building structure and parameter uncertainty. It is an extension of traditional nonlinear time-history analysis, and this kind of method is wildly used for seismic performance evaluation. According to IDA, for single seismic ground motion, different amplitudes are chosen, denoted as IM (Intensity Measure). During calculation process, corresponding nonlinear time-history analysis is conducted when amplitude of seismic ground motion is changed. And the damage measure (DM) of the building structure is therefore marked. In a two-dimensional coordinate system, the IDA curves can be obtained by measures of IM and DM.

By using this method, when building structure is suffered different intensities of earthquake, their responses to the whole earthquake process can be obtained by analyzing a few earthquake waves. Thus, complete seismic behavior evaluation of building structure can be realized. Meanwhile, collapse resistant capacity f building structure can also be studied, which can reflect real resistance level of building structure.

At present, during the process of seismic behavior analysis, the positions of each behavior of the engineering structure should be pointed out in the IDA curve when adopting IDA method. As a result, there is an obvious elastic stage of IDA curve from origin to the point where ${\theta }_{max}$ is about 1 %. Then there follows a yielding stage of IDA curve, and the tangent slope of the curve is elastic stiffness, $Ke$.

According to request of FEMA351, the point where slope of IDA curve begins to change means that the structure can continue to work. When slope of IDA curve is less than 0.2$Ke$, it is the point (Collapse Prevention, CP) that means the structure is in a limit state of no collapse. If the extreme value, ${\theta }_{max}$, of the story drift angle is more than 10 %, then ${\theta }_{max}$ is 10 %. After this point (Global Dynamic Instability), the IDA curve begins to become a, which means that the whole structure is in a state of dynamic instability.

During calculation process, acceleration spectra, $Sa$, is used as intensity measure of seismic ground motionfor IDA method, and the acceleration spectra correspond to structural period with damping ratio of 5 %, which is denoted as (T1, 5 %). Moreover, the maximum story drift angle is used as a damage measure (DM). Combined with the selected IM and DM, seismic behavior of the new assembled monolithic concrete structure is further studied.

4. Seismic wave selection

The key to incremental dynamic analysis lies in how to select reasonable seismic inputs. The calculation model in this article is established according to real engineering structure. Therefore, when using IDA method, strong motion recordings should be selected according to site classification of the real engineering.

For research object, its design bases should be taken into consideration, so 20 strong motion recordings are used as seismic input for IDA, as shown in table 1. These recordings are among 6 and 8 earthquake magnitudes, and they bare selected from seismic recordings database in Pacific Earthquake Engineering Research Center, which is helpful for seismic behavior evaluation of the model with the influence of object earthquake.

5. Result analysis

By using the method of hunt&fill, amplitude modulations of the above mentioned 20 earthquake waves can be realized. Thus, the IDA curve can be plotted, as shown in Fig. 6.

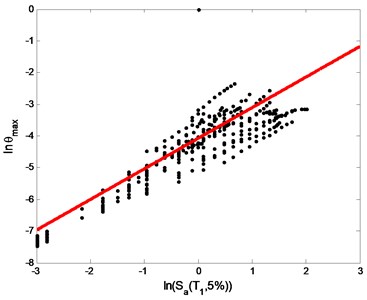
Fig. 5 shows the IDA curves of the new assembled monolithic concrete structure. Fig. 6 shows linear regression analysis of IDA curves. Further analysis shows that with the influence of same earthquake magnitude, both maximum story drift angle and maximum bearing capacity of the structure can meet with requests of the current Chinese seismic design code.

Meanwhile, when the new assembled monolithic concrete structure is suffered with earthquake, both seismic motion amplitude and seismic parameters tend to become lower, which means the damage degree is lower when the structure is under the influence of same earthquake magnitude

Fig. 5The IDA curve

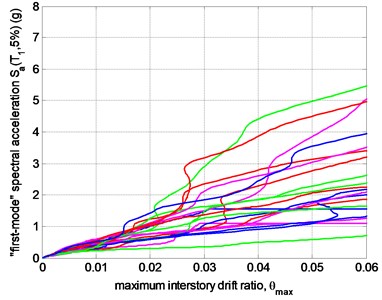
Fig. 6Linear regression analysis of IDA curve

6. Conclusions

Elastoplastic time-history analysis of the new assembled monolithic concrete structure is conducted through the method of incremental dynamic analysis, and IDA curves of the structure are plotted as well. Some conclusions can be obtained as follows:

1) Results of incremental dynamic analysis shows that seismic behaviors of the new assembled monolithic concrete structure can meet with requests of the current Chinese seismic design code.

2) Seismic behaviors of the structure are analyzed according to the features of the structure and the current Chinese seismic design code. Results show that seismic behaviors of the new assembled monolithic concrete structure are better than those of traditional reinforced concrete frame structure. With the influence of same seismic ground motion intensity, damages of the new assembled monolithic concrete structure are less than those of traditional reinforced concrete frame structure.