Abstract
Flywheel energy storage system (FESS) will be needed at different locations in the wind farm, which can suppress the wind power fluctuation and add value to wind energy. A FESS that can store up to 3.6 kWh of usable energy in 12 minutes at a maximum 24,000 r/m was designed. Multiple flywheels can be interconnected in an array, or matrix, to provide various megawatt-level power capacities for the wind farm. Based on ANSYS software, the finite element model of the flywheel was built to calculate the stress and strain field at different rotating speed. The maximum theoretical rotational speed and the peripheral velocity of the flywheel can be obtained. The flexible modes of the rim-hub-shaft system were also analyzed by ANSYS. The results indicated that the flywheel could run at the rated speed of 24,000 r/m safely. The running tests showed that the flywheel can smoothly pass through the two critical speeds, which was helpful for subsequent running tests.
1. Introduction
Due to the energy problem and environmental problems, countries around the world are actively developing wind power in recent years. The wind power capacity of the world has a rapid increase. However, wind power fluctuations have adverse impacts on power quality, such as grid voltage and system frequency. The Energy storage devices will be needed at different locations in the power system, to level the mismatch between renewable power generators and consumption and/or to store the surplus of power from renewable sources for later use during non-generation time periods or low power generation time periods [1]. The flywheel energy storage technology has advantages of the rapid charge and discharge, long life, high efficiency, which can effectively improve the quality of power supply and smooth wind power fluctuations [2, 3].
The excess electrical energy is stored as kinetic energy of a rotating flywheel rotor and is converted to electrical energy when needed in a FESS. The rise and fall of the rotating speed of the flywheel realizes the storage and release of the electrical energy. As a new way of energy storage, flywheel can play a different role corresponding to the types of the wind turbines. Flywheel can be used as an energy storage device to adjust the output power in a small isolated grid. The power electronic converters and control modules start the flywheel to charging and discharging according to the signal of real-time monitoring of the wind turbine. Flywheel system based on control method of current feed-forward can adjust the output power of the variable-speed wind turbine efficiently [4]. In the combined application of the wind turbine and diesel-driven generator, flywheel compensates reactive power except for regulating voltage. The flywheel in literature stores energy about 4.5 MJ, which can reduce the impact of fluctuations of wind energy effectively and compensate reactive power [5]. It supplies power to the whole system for 1.8 minutes, which gives the standby diesel engine sufficient time for the restart. The capacity of large-scale wind farm has an increased proportion in the total grid, and the impact is getting larger after wind power integration. The FESS is centralized or distributed in the wind farm depending on the type of wind turbine, the size of wind farm and the capacity of the local power grid [6-8].
The study on application of FESS for wind power system is still in the theoretical modeling and simulation stage. The application research is still relatively inadequate. In order to carry out the basic research of FESS for wind power system, Tsinghua University and China Electric Power Research Institute had developed a 20 kW/3.6 kWh FESS. Its charge-discharge process lasted about 25 minutes and the maximum speed was 24,000 r/m. The structural strength of the flywheel and its dynamics directly determine whether the flywheel can be accelerated to the working speed and runs stably. Based on the finite element software ANSYS, the structure stress field was calculated when flywheel was rotating at the maximum speed. The dynamic model of the flywheel rotor-bearing system was built to calculate mode shapes and modal frequency with different speed and critical speeds can be obtained. The results provided a reliable theoretical basis for optimization and improvement of the FESS.
2. Structural analysis of the flywheel rotor
2.1. Diagram of the flywheel rotor
The flywheel rotor consists of core shaft, hub and rim. The rim is supported by the hub. Both the hub outer diameter and the inner diameter of the composite rim are tapered with the same angle. A permanent magnet motor/generator is mounted on the shaft. The rated power of the motor is 20 kW and its rated speed is 24,000 rpm. There is a permanent magnetic bearing at the top to levitate the 80 % weight of flywheel, which makes the spiral groove bearing at the bottom avoid severe wear and significantly reduce the friction power. The physical parameters of the flywheel rotor is shown in Table 1.
Fig. 1The flywheel rotor
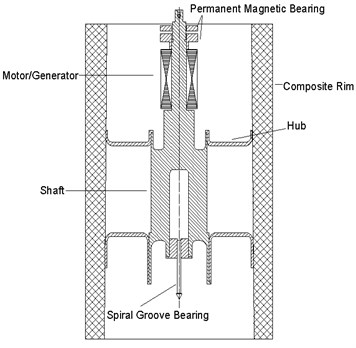
Table 1Parameters of the flywheel
Mass (kg) | 150 |
Diameter of rim (mm) | 500 |
Length of rim (mm) | 800 |
Polar moment of inertia (kg∙m2) | 5.5 |
Diameter moment of inertia (kg∙m2) | 8.7 |
Stored energy (Wh) | 3600 |
2.2. Hub-rim stress analysis
The hub transmits torque from shaft to rim. The magnitude of interference is 0.2 mm between shaft and hub. So is the hub at the bottom and rim. The hub has small stiffness which compensates the deformation difference between the rim and the shaft under the high speed running condition. The kinetic energy stored in flywheel is proportional to the square of its speed, which is mostly limited by the strengths of the materials and structure centrifugal stress. So composite materials should be used for manufacturing the rim. However, the transverse strength of the filament wound flywheel is much lower than the hoop one, which makes the each ring of the rotor separate at rotation easily. The mechanical properties of flywheel materials is the shown in Table 2.
Table 2Mechanics parameters of the flywheel materials
Component | Materials | Ex (GPa) | Ez (GPa) | ρ (kg/m3) | σLS (MPa) | σTS (MPa) | σb (MPa) |
Rim | CFRP | 10 | 155 | 1650 | 1800 | 50 | – |
Hub | 7050 | 71 | 71 | 2850 | – | – | 590 |
Shaft | 40Cr | 210 | 210 | 7850 | – | – | 785 |
The plane axial-symmetrical model was used to calculate the stress of flywheel under rotation centrifugal load in FEM analysis. In the elastic calculation, the first load step is interference fit when rotating speed is zero, the second load step is centrifugal load under the rotational speed of 400 r/s. The highest von Mises stress of the aluminum alloy hubs is 489 MPa, being lower than the stress limit of aluminum alloy 7050. The maximum stress value of the composites rim was shown in Table 3. The rim materials are safe while the maximum stress failure criterion could be applied.
Table 3The maximum stress in rim
Materials | σr (MPa) | σθ (MPa) | σy (MPa) | σLS (MPa) | σTS (MPa) |
CFRP | 12.7 | 658 | 4 | 1800 | 50 |
Fig. 2 displayed the radial displacement of hub and contact pressure of shaft/hub/rim. The hub will expand 0.79 mm in radial direction. There are large contact press between the hub and the rim, which make sure the two parts keeping in fixed contact. The calculations above show that the flywheel structure is safe when it rotates at 400 r/s.
Fig. 2Radial deformation of hub and contact pressure of shaft/hub/rim (400 r/s)
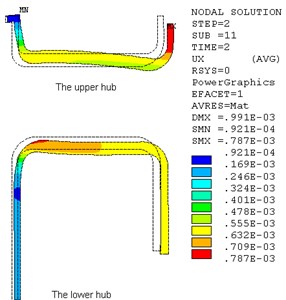
a)
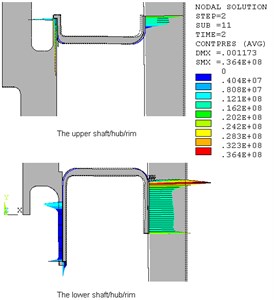
b)
3. Dynamics modeling and simulation of the flywheel-bearing system
3.1. Modal vibration analysis
In order to install the motor, shaft is long and thin and its bending vibration frequency may be lower than working speed of flywheel. The stiffness of the thin hub may be not high enough to make the flexible modal frequency of the rim-hub-shaft system being bigger than the rated rotational frequency. Both problems make elastic vibration of flywheel appear, which cause the system to be unstable. Modal vibration analysis is necessary for flywheel rotor-bearing system. ANSYS was used to establish the dynamic model of the dynamic system. The COMBIN214 and MASS21 were selected to model the top and bottom support of the flywheel. The SOLID186 that includes gyroscopic effect was appropriate for modeling the flywheel rotor.
When rotating speed is zero, modal frequencies and mode shapes of the system are shown in Fig. 3. It can be seen that the flywheel rotor-bearing system has two rigid-body vibration modes: cylindrical mode of the flywheel rotor and its modal frequency is 13 Hz, conical mode of the flywheel rotor and its modal frequency is 50 Hz. The analysis also indicates that there are two flexible modes with frequency under 600 Hz. The first is a “hub axial” mode, when the hub deforms mainly in axial direction, with the frequency of 106.9 Hz. The second modal frequency is 539 Hz, where the modal shape is expressed as the bending of the core shaft. Due to bending frequency of shaft is much higher than the working speed 400 r/s, the dynamics of the system is safe. The hub axial mode has little effect on system stability.
Fig. 3Flexible hub-rim-shaft modes
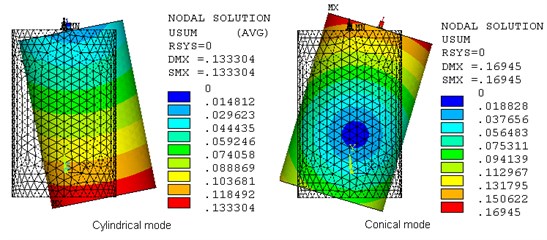
a)
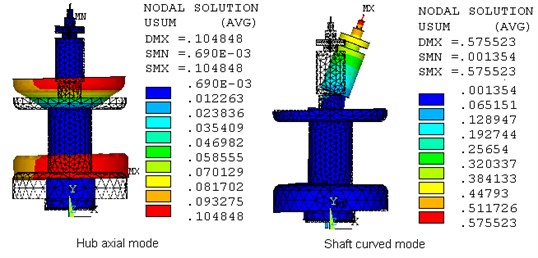
b)
3.2. Critical speeds
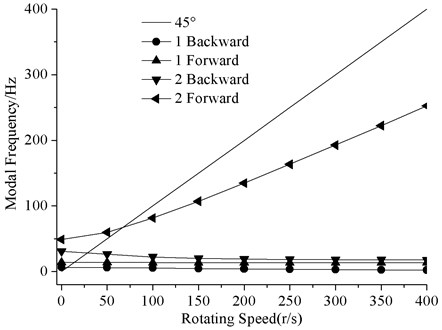
By means of APDL programming, the mode frequencies of the flywheel rotor dynamic system with different speed is obtained and shown in Fig. 4. In Fig. 4, ‘1F’ and ‘1B’ indicate the first-order forward and backward whirl of the flywheel respectively, ‘2F’ and ‘2B’ indicate the second-order forward and backward whirl of the flywheel respectively. Critical speeds occur at the peak response speed when the forward whirl frequency is excited by the rotating speed that can produce synchronous unbalance. The critical speeds are 15 r/s and 70 r/s. There is no critical speed in the working speed range 200 r/s-400 r/s, the dynamic design is appropriate.
3.3. The running tests of the flywheel system
After the high-speed balancing, the vibration amplitudes of both ends of the flywheel rotor were less than 10 μm when rotating speed was 4796 r/m. The flywheel shafting will pass the second-order critical speed that corresponding to conical mode as rotating speed increases. The vibration amplitudes were small when it passed the second-order critical speed till the design speed.
Fig. 4Mode frequencies with different speed
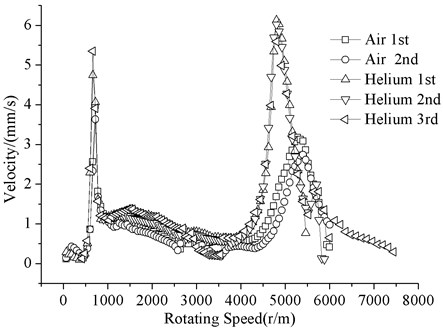
Two running tests were carried out in the atmospheric environment. In order to reduce air friction losses, three running tests were also carried out. Fig. 5 shows the vibration of all five tests. The maximum rotating speed has reached 7500 r/m. In the helium environment, the first-order critical speed of flywheel shafting was unchanged, and the peak vibration increased slightly. The second-order critical speed was reduced to 4200 r/m, and the peak vibration increased doubled. The critical speeds in the running test were close to the numerical results. Due to the viscous damping of Helium was much smaller than air, which caused resonance peak in the Helium be much bigger. It was estimated that changes of bearing parameters made the critical speeds decrease.
Fig. 5Amplitude-frequency curve of operation
4. Conclusions
1. The structural stress analysis indicated that the material failure would not happen when the flywheel was speeded up to 400 r/s. The hub would expand 0.79 mm in radial direction. There were large contact press between the hub and the rim, which made sure the two parts keeping in fixed contact. The calculations above showed that the flywheel structure was safe when it rotates at 400 r/s.
2. The modal analysis of the flywheel rotor-bearing system indicated that both the rigid modes and the flexible modes were presented in the system. The system had two rigid-body vibration modes: cylindrical mode of the flywheel rotor and its modal frequency was 13 Hz, conical mode of the flywheel rotor and its modal frequency was 50 Hz.
3. Due to bending frequency of shaft was much higher than the working speed 400 r/s, the dynamics of the system was safe. The hub axial mode had little effect on system stability. The critical speeds were 15 r/s and 70 r/s. There was no critical speed in the working speed range 200 r/s-400 r/s, the dynamic design was appropriate. The running tests showed that the flywheel can smoothly pass through the two critical speeds, which was helpful for subsequent running tests.
References
-
Robert B. S. Executive overview: energy storage options for a sustainable energy future. IEEE Power Engineering Society General Meeting, Vol. 2, 2004, p. 2309-2314.
-
Hebner R., Beno J., Walls A. Flywheel batteries come around again. IEEE Spectrum, Vol. 39, Issue 4, 2002, p. 46-51.
-
Lawrence R. G., Craven K. L., Nichols G. D. Flywheel UPS. IEEE Industry Applications Magazine, Vol. 9, Issue 3, 2003, p. 44-50.
-
Roberto C., Rubén P. Control strategies for enhanced power smoothing in wind energy systems using a flywheel driven by a vector-controlled induction machine. IEEE Transactions on Industrial Electronics, Vol. 48, Issue 3, 2001, p. 625-635.
-
Iglesias I. J., Garcia L. Design and simulation of a stand-alone wind-diesel generator with a flywheel energy storage system to supply the required active and reactive power. IEEE 31st Annual Power Electronics Specialists Conference, Vol. 3, 2000, p. 1381-1386.
-
Rion T., Li Wu, Toshiaki M. An application of flywheel energy storage system for wind energy conversion. International Conference on IEEE PEDS, Vol. 2, 2005, p. 932-937.
-
Gabriel O., Christophe S., Benoît R. Control and performance evaluation of a flywheel energy-storage system associated to a variable-speed wind generator. IEEE Transactions on Industrial Electronics, Vol. 53, Issue 4, 2006, p. 1074-1085.
-
Barote L., Georgescu M., Marinescu C. Smart storage solution for wind systems. IEEE Bucharest PowerTech, 2009, p. 1-6.
About this article
This work was financially supported by the foundation of CEPRI.
