Numerical calculation and finite element calculation on impeller of stainless steel multistage centrifugal pump

2.1. Theory on flow field calculation

According to Bernoulli equation, pump experimental head is:

where $p_d$ and $p_s$ are fluid static pressure on outlet and inlet section, $v_d$ and $v_s$ are fluid velocity on outlet and inlet section, $z_d$ and $z_s$ are the distances to base level from outlet and inlet section. The efficiency of pump is the ratio of effective power to shaft power, and is represented by:

where $P_{\xi }$ is the effective power, $P_t$ is the shaft power, $Q$is volume flow, $M$ is the sum torque on shaft, and $\omega$ is angular velocity of impeller. After applying the results of flow field calculation, the pump performance curve is obtained.

2.2. Theory on fluid structure interaction

Fluid solid interaction (FSI) mechanics is the interdisciplinary branch of fluid mechanics science and solid mechanics science. It mainly studies the deformation and movement of solids in the flow field, as well as the impact of this behavior to the flow field. In order to check the impeller strength and predict the exact location of maximum stress on impeller directly, flow field calculation and finite element calculation can be combined together by using FSI.

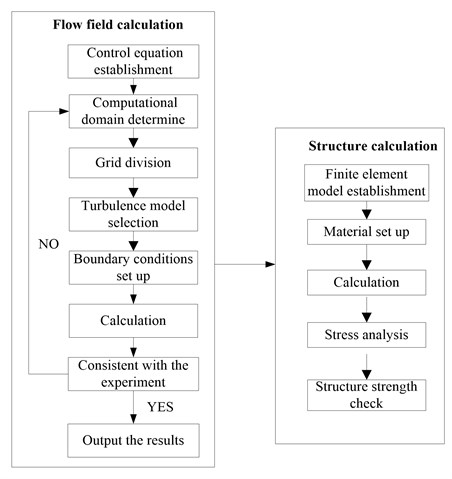
The solving of FSI problems is comprised of two-way coupling and unilateral coupling. The former one means all unknown quantities in both fluid field and solid field are solved at the same time step according to common coupling equations, while the latter is a kind partition iterative solving that means the data is unidirectional when transferring on coupling interface. For inner flow field, the solid deformation influence may be neglected because the deformation of impeller is very small. Thus, unidirectional FSI method is used in this paper and the flow table is shown in Fig. 1.

Fig. 1Computational flow table

3.1. Hydraulic design of model pump

The stainless steel multistage centrifugal pump of 100XQJ8 is selected in the studies. Its design parameters are listed as below: rated flow $Q=$8 m³/h, single stage head $H=$4.5 m, rotational speed $n=$2850 r/min, maximum power $P=$3 kW, and the total head $H=$72 m. In view of the structural condition that the outer diameter of multistage well pump is limited by well diameter, Lu Weigang [19] studied a design method of well pump, the impeller maximal diameter design method, which expands the front shroud of impeller to the edge of pump wall and makes the impeller diameter achieve maximum value while well diameter is invariable.

Impeller with five different blade thicknesses (${\delta }_1=$0.5 mm, ${\delta }_2=$1.0 mm, ${\delta }_3=$1.5 mm, ${\delta }_4=$2.0 mm, and ${\delta }_5=$2.5 mm) are designed as research objects. The geometric parameters are shown in Table 1.

There is an impeller model displayed in Fig. 2(a), whose blade thickness is 1.5 mm. The impeller is in coordination with reverse diffuser, which can shorten the axial length of well pump to the minimum. The main parameters of reverse diffuser are listed as below: the number of blade $Z=$8, inlet width $B_3=$6.2 mm, inlet diameter $D_5=$75 mm, and outlet diameter $D_6=$37.5 mm. Reverse diffuser is shown in Fig. 2(b).

Fig. 2Three-dimensional diagram of impeller and reverse diffuser

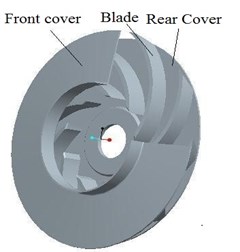
a) Impeller

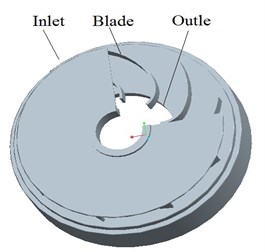
b) Reverse diffuser

3.2. Fluid calculation model

3.2.1. Computational domain

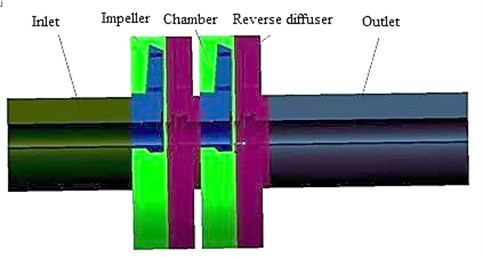
Stainless steel stamping centrifugal pump is one of multi-stage pumps. Compared with single-stage pump, the structure of multi-stage pump is more complex and its flow characteristics are different. Therefore, it’s particularly important to select appropriate series when making numerical simulation for multi-stage pump. I have ever done relevant research. Four different series in a numerical simulation with the blade thickness of 1.5 mm are selected and the efficiency and head at all series are shown in Table 3 and Table 4. As can be seen from Table 3 and Table 4, the efficiency and head of the first-stage in different stages are almost the same. When the series is $n\ge$2, there is little difference between the second stage and the following, but the difference is big compared with the first stage. It is also consistent with the fact that the flow in the first impeller inlet of multi-stage pump is usually irrotational while rotational in the other impeller inlet. Taking into account that increase of stage will bring about more cell number, thereby demand computer with higher performance, so the two-stage model is selected and the efficiency as well as head of the second stage are taken as performance prediction value. In the numerical calculation of the pump, the water part in the pump is meshed by many small cells. The pump water model is consist of inlet section (water), two impellers (water), two chambers (water), two reverse diffusers (water), outlet section (water), which is shown in Fig. 3.

Table 2Efficiency comparisons of different stages

Series ($n$)	1	2	3	4
The first-stage efficiency (%)	59.51	59.93	59.79	59.86
The second-stage efficiency (%)		62.50	62.53	62.53
The third-stage efficiency (%)			62.59	62.58
The fourth-stage efficiency (%)				62.61
The total efficiency (%)	56.57	59.55	60.12	60.14

Table 3Head comparisons of different stages

Series ($n$)	1	2	3	4
The first-stage head (m)	4.745	4.762	4.758	4.755
The second-stage head (m)		4.611	4.605	4.612
The third-stage head (m)			4.608	4.621
The fourth-stage head (m)				4.628
The average head (m)	4.511	4.588	4.595	4.597

Fig. 3Pump water model

3.2.5. Test rig setup

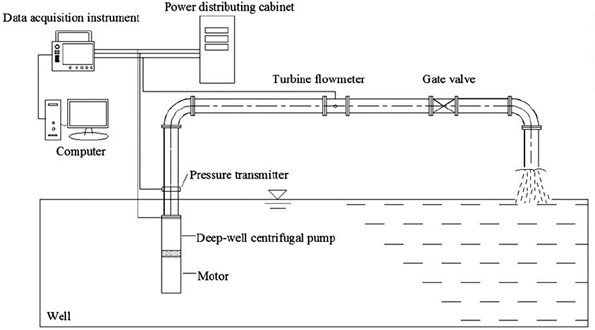
Experiments were done in an open-type pump system, which have the identification from Jiangsu Province of China. The test rig is composed of two parts, namely, the data acquisition system and the water circulation system. The data acquisition system changes all kinds of physical quantities at different conditions, while the water circulation system supplies the necessary environment for centrifugal pump operation. The test rig is shown in Fig. 4. A turbine flowmeter was used to measure the flow $Q$ and the precision of turbine flowmeter is ±0.3 %. Speed is measured by a tachometer (PROVA RM-1500, Taiwan). During the experiment, only one dynamic pressure transmitters (CYG1401) was used to measure the outlet pressure. The precision of CYG1401 is ±0.2 %.

Fig. 4Test ring of multistage well pump

3.2.6. Experimental results

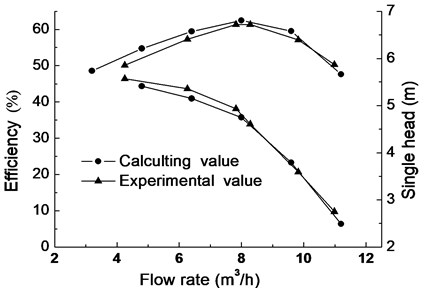
Fig. 5 is comparison between experimental value and calculating value of multistage pump with the blade thickness of 1.5 mm. It can be seen from Fig. 6, calculating value and efficiency value coincides perfectly and deviation is less than 1 % at design flow rate while calculating flow field is not same as the real one at un-designed flow rate. Hence, the calculating result has more than 3 % deviation compared with experimental result.

There are three main reasons making deviation. Firstly, at small flow rate, the liquid in the impeller and return diffuser is easy to produce flow separation or vortex. Secondly, in order to set modeling and calculation, the model is simplified to some extent in the process of simulation. Thirdly, due to the limitations of stamping process, model of simulation has some deviation to real model. Overall, calculation value is close to experimental value, and numerical calculation is credible at a certain extent. Thus, in order to analyze inner flow field and strength of impeller, numerical simulation in the study is adopted.

Fig. 5Comparison of calculating and experimental value

3.3. Element model of impeller

The finite element analysis of the impeller in this paper is based on ANSYS Workbench and the impeller is made of stainless steel 0Cr18Ni9, whose basic property is listed in Table 7.

The structural cell of impeller is divided freely, and calculating model has 129654 cells and 248258 nodes. The impeller is connected with quincunx shaft and shaft sleeve is used to realize axial locating between impellers. To set constraint condition conveniently, the intersection between impeller and shaft is simplified as circular holes plane and constrained with cylindrical plane. Loads on impeller include inertial force and surface force. Inertial force is mainly caused by the rotation speed while surface force by the fluid pressure impacting on impeller surface. The interfaces between the impeller and fluid (all of blade surfaces, inner surfaces and outer surfaces of impeller cover) are set as Fluid Solid Interface.

4.1. Effect of blade thickness on pump performance

The theoretical head is drawn from Euler equation of pump:

In the equations above, $u_1$ and $u_2$ are peripheral speed at blade inlet and outlet, $v_{u1}$ and $v_{u2}$ are peripheral component of absolute speed at inlet and outlet, $g$ is the acceleration of gravity, $Q_t$ refers to theoretical flow, $h_0$ is Stodala slip coefficient, $D_2$ is outlet diameter of impeller, ${\beta }_2$ is blade outlet angle, $z$ is number of blades, and ${\phi }_2$ is outlet crowding coefficient. Law could be found from Eqs. (4) and (5) that smaller ${\phi }_2$, that is, thicker blades may bring steeper head curve. Under the same conditions, five impeller models with different blade thicknesses are calculated by ANSYS Fluent, and the performance curves are shown in Fig. 6.

Fig. 6Performance curve with different blade thicknesses

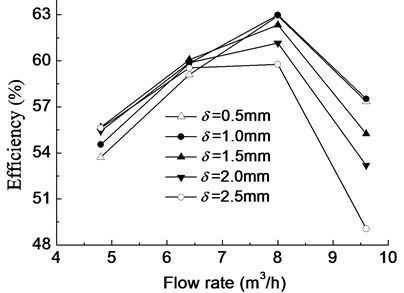
a) Efficiency curve

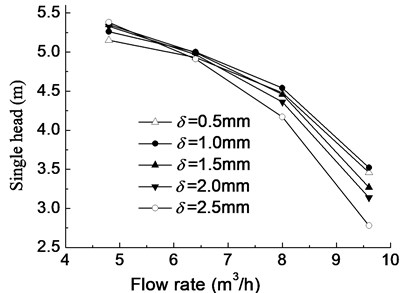
b) Head curve

According to Fig. 3, the inlet section and outlet section are at the same height, so $z_d-z_s=$0, and the Eq. (1) can be simplified to the Eq. (7) as follows:

In the Eq. (7), $P_d$ and $P_s$ show the total pressure on outlet and inlet section, and theycan be obtained through the post-processing in the ANSYS Fluent, so the head $H$ can be calculated through the Eq. (7). Moreover, the sum torque on shaft $M$ can also be gained through ANSYS Fluent, the flow rate $Q$ and the angular velocity of impeller are known quantities, so the efficiency $\eta$ can be calculated through the Eq. (2).

As can be seen from Fig. 6, the change of impeller blade thickness impacts on efficiency and head significantly, and the head curve becomes steeper with the increase of impeller blade thickness. At the design flow rate and large flow rate, the efficiency and single-stage head decrease as the increase of impeller blade thickness while instead at small flow rate, which indicates that the best efficiency point of the pump shifts to the small flow direction with the increase of impeller blade thickness. The efficiency and head change a little at design flow rate when impeller blade thickness changes from 0.5 mm to 1.5 mm. If it exceeds 1.5 mm, with the increase of thickness, the efficiency and head decrease rapidly. This means the thickness should be limited within a reasonable range.

Table 8Stress distribution for impellers with different thicknesses

Blade thickness	Inertia load	Fluid load	Combination of both loads
0.5 mm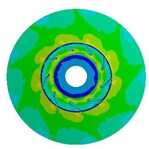
1.5 mm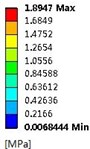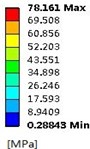
2.5 mm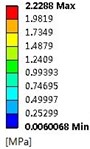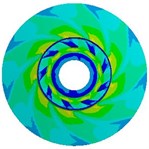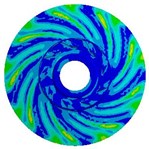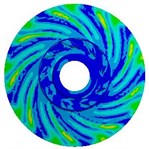

4.2. Effects of impeller loads on stress

Loads on stainless steel impeller consist of inertial force load caused by impeller rotation speed and fluid pressure load when pump is working. In order to compare the influence of the two loads on impeller, this study calculates respectively inertial force load, fluid pressure load, and both loads at design flow rate on stress and deformation of impeller. Table 8 means the stress distribution of impellers whose blade thicknesses are 0.5 mm, 1.5 mm, and 2.5 mm. The table indicates stress distributions on three impellers are similar. The maximum stress by fluid pressure load is much greater than those brought by inertial force load, while slightly smaller than those brought by both of them, which means that the load brought by high-pressure fluid plays a dominating role in stress distribution. Affected by three different loads, stress on impeller distributes in circumference and it is apparently larger at the inlet of blade. Besides, when the radius is the same, the stress at intersection between impeller and cover is obviously larger. With the increase of blade thickness, the maximum stress caused by inertial force load gradually increases, while the maximum stress of fluid pressure load decreases. That’s because thicker blade brings heavier impeller and larger stress caused by inertial force. Moreover, thicker blade increases the area of intersection between blade and cover, which makes impeller steady and reduces the maximum stress caused by fluid pressure. If the blade thickness is 0.5 mm, the maximum stress caused by both of the two loads is 277.29 MPa (kg/cm²) which exceeds the stainless steel’s yield strength ${\sigma }_s=$207 MPa; if it is 1.5 mm and 2.5 mm, the maximum stress are respectively 78.16 MPa (kg/cm²) and 50.69 MPa (kg/cm²). But the over-thick blade not only increases the cost of impeller, but also reduces the performance of pump. Hence, as a reasonable value of blade thickness of impeller, 1.5 mm is selected at last.

Table 9Deformation distribution for impellers with different thicknesses

Blade thickness	Inertia load	Fluid load	Combination of both loads
0.5 mm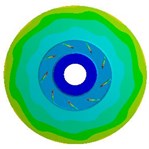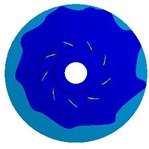
1.5 mm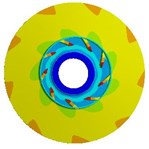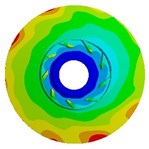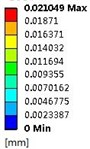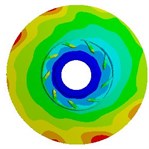
2.5 mm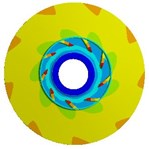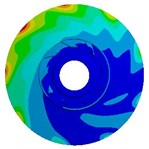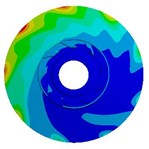

4.3. Effects of impeller loads on deformation

Table 9 shows the deformation distribution of impellers whose blade thicknesses are 0.5 mm, 1.5 mm, and 2.5 mm. The table indicates deformation distributions on three different impellers are similar. The maximum deformation caused by fluid pressure load is much greater than those caused by inertial force load and slightly smaller than those caused by both of them, which is similar to stress distribution illustrated above. When the thickness is 0.5 mm, the deformation caused by inertial force load increases gradually along the flow direction from inlet to outlet and at the outlet of front shroud it reaches the maximum value, while the deformation by fluid pressure load gets the highest at the blade inlet because equivalent stress here is too large and blade is too thin. Maximum deformation caused by three loads gradually decreases with the increase of blade thickness, but the position where maximum deformation appears transfers from blade inlet to outlet of front shroud. In addition, due to relatively high rigidity of cylindrical interface between the impeller and shaft, deformation in this position is always small for all load cases.