Vibration characteristics of the impeller at multi-conditions in mixed-flow pump under the action of fluid-structure interaction

2.1. Physical model

In this paper, the main parameters of the mixed-flow pump are as follows: flow rate $Q_{des}=$380 m³/h, head $H_{des}=$6 m, rotate speed $n=$1450 r/min, specific speed $n_s=$480, number of blades $Z=$4, number of guide vanes $Z_d=$7. The calculation domain are the whole segments from the inlet segment of pump to the outlet segment of the circular volute chamber. Three-dimensional modeling of inlet segment, impeller, guide blade, circular volute chamber and outlet segment is established respectively using the Pro/Engineer software. 3D models of impeller and guide vane are shown in Fig. 1.

Fig. 1Three-dimensional models

a) Impeller

b) Guide vane

2.2. The fluid-structure coupling calculation model and mesh generation

The material the impeller of the mixed-flow pump model is steel, its elasticity modulus is 2.06×10¹¹ Pa, Poisson’s ratio is 0.3, density is 7.85×10³ kg∙m^-3, modulus of rigidity is 7.6923×10¹⁰ N∙m^-2, yield strength is 2.5×10⁸ N∙m^-2.

Considering the tip clearance is very small relatively to the size of the impeller, and in order to ensure the enough number of grid cell in the tip clearance, effective number of nodes and the uniform transition from tip clearance grid to the internal grid of impeller. Mesh of fluid zones are generated by the hexahedral mesh. In the impeller and the guide vane, the J/O topological structure and the H/O topological structure are adopted respectively. The Y-block topological structure is used in the inlet section and the flow passage is formed by the periodic array. The grid is changed uniformly according to the curvature of each wall by controlling the node of each topology line and encryption processing is carried out in the impeller. The total grid number of flow field calculation domain is about 1.1001 million, and the impeller calculation domain unit is about 461100, guide vane calculation domain unit is about 453700, and the total number of nodes is 1.017 million. When the computing grid number is over 1.1001 million, the change of head is very small with the increasing of grid number. The error of calculation is within ±5 %, which conforms to the requirements of the grid independence test. The y⁺ of the whole calculation domain is less than 100, that is, the grid nodes of the first layer are located in the layer of logarithmic law, and the boundary layer is processed by the standard wall function accordingly. The fluid surfaces with different boundary conditions or contacting with different walls are set as different PART in the process of meshing. So that the different boundary conditions and the coupling interface can be flexibly and correspondingly set in the CFX software. Fluid meshing is shown in Fig. 2.

Fig. 2Mesh in fluid zone

Fig. 3Mesh in structure zones

Mesh of structure zones are generated using grid automatic generating function in the Workbench. The dots, lines, surfaces and entities of the rotor model are fully converted into the simulation module of the Workbench with the seamless docking function between ANSYS 14 components and PRO/E software. Meanwhile, the structural finite element mesh is generated using the Automatic meshing mode in Mesh functions, which is shown in Fig. 3. Furthermore, the corresponding coordinates of the two solving domains in the respective solver are to be maintained, so that the relative positions of the two solving domains are the same, to ensure that the fluid interface and the contiguous solid interface correspond with each other correctly.

2.3. The realization process of the fluid-structure interaction calculation

The flow field is calculated in the CFX software and the transient dynamics analysis of the solid structure is carried out in Workbench ANSYS. The results of steady calculation as the initial value of unsteady flow field calculation. The flow field and structural response are individually calculated before the fluid-structure coupling synchronization solving. If the two fields both could obtain the satisfactory results without considering the impact of external field, the fluid-structure coupling synchronization solving can be carried out simultaneously to ensure the calculation go with a swing.

In the structure field solver ANSYS Workbench, the transient dynamic analysis of the structure is used to realize the synchronous solution with the calculation of the unsteady flow field, and the transient dynamic analysis install the corresponding external loads and the fixed constraints. For the structure in the fluid-structure coupling solution, the external load is the action of fluid force on the structure surface, so the surface which the impeller and fluid contact with each other is set as the fluid solid interface and the pressure load produced by the fluid is applied on the structure. The impeller is set to the corresponding fixed support, as shown in Fig. 4 with blue marks. The solving time and step length is set to be the same as these of the unsteady flow field calculation in the CFX software. In the coupling calculation, the fluid calculation grid will deform under the action of fluid-structure interaction, therefore, it needs to be provided by using dynamic mesh technology in the CFX software to solve the problem and set the analog type as transient mode.

In order to get the stable results, the unsteady flow field and the structural response within the time when the impeller rotates 4 times have been calculated. By monitoring, after fluctuation process at the beginning of the calculation, the pressure fluctuations of the unsteady flow field in the impeller and the change of the axis offset of the impeller are basically stable. Therefore, the fourth lap of impeller rotation is chosen to analyze. The instantaneous flow field is solved using the Second Order Backward Euler scheme, and the residual error convergence target of flow field calculation at each time point is 10^-4. The relaxation factor of coupling calculation during data transfer process is 0.75, and the convergent standard is 10^-3.

Fig. 4A schematic diagram of loads and constraints of the rotor

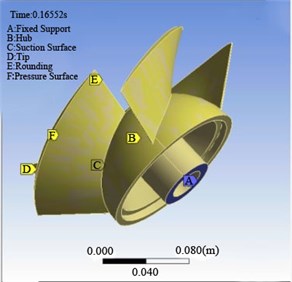
Fig. 5Experimental setup: 1 – mixed-flow pump, 2 – test line, 3 – surge tank

3.1. Testing apparatus

A closed test rig for mixed-flow pump is set up to verify the accuracy of the numerical simulation. The test rig is suitable for diameter 250 mm axial flow pump, mixed-flow pump and model device, as shown in Fig. 5.

In this test, the rotating speed, torque and shaft power of the model pump were measured using ZJ type torque tachometer connected between the rotor and model pump shaft, which was produced by Shanghai-standard Intelligent Terminal Co., Ltd. The pump head was measured using MPM type pressure sensor produced by Mike Company. The pump flow was measured using LWGY type turbine flow-meter produced by Shanghai ZiYiJiu Company. High frequency pressure sensor was installed at the inlet and outlet of pump section, by using 0-24v DC power source for power supply, and the raw output is 0-5 V voltage signal. All the signals were collected automatically and sent to the computer and displayed on the screen. The measurement errors of tachometer and flow meter are ±0.2 % and ±0.5 %, respectively. The accuracy level of pressure gauge is 0.4, and the test rig reaches the level 1 accuracy requirement.

3.2. Test result and analysis

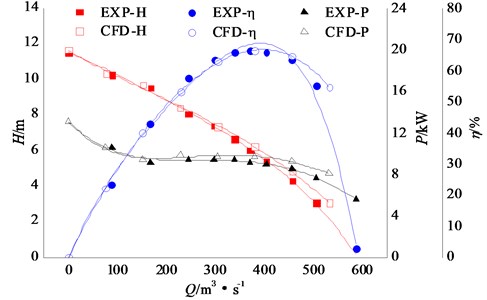
The predicted external characteristic was compared with the experimental external characteristic, as shown in Fig. 6. In this figure, the experimental results named EXP are showed by solid symbol and the numerical simulation results named CFD are showed by the hollow symbol. It can be seen from the figure, the calculated head value is higher than the model test, but the efficiency is lower than the experimental test results slightly. At small flow rate condition, the results of numerical simulation and experiment are very similar. At the highest point of efficiency, the error of head and efficiency is separately 3.29 % and 0.2 %. Due to the local structure difference for pumps used in the comparison of numerical calculation model and test measurement and other effects such as mesh quality, it is inevitable to exist the error of numerical calculation and test measurement. However, as a whole, the head and efficiency of numerical simulation are generally consistent with the performance of test measurement, which indicates that the flow field calculation model can accurately predict its performance. By solving the model, it can accurately obtain the pressure load information of the impeller blade surface, which provides guarantee for the impeller finite element analysis.

Fig. 6Comparison between experimental external characteristics and numerical results

4.1. Pressure distribution of blade surface under various flow rate conditions

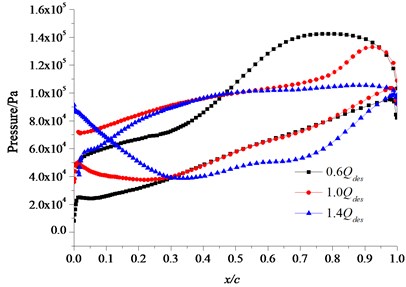
The distribution of the flow field in different flow rate conditions is obtained by the calculation of the three-dimensional flow field. The pressure field under small flow rate (0.6$Q_{des}$) condition, design flow rate (1.0$Q_{des}$) condition and large flow rate (1.4$Q_{des}$) condition are chosen and compared. Fig. 7 is the distribution of pressure along with the chord line of the different section at the location of different blade height. The $x$-coordinate ($x/c$) presents the ratio of the distance $x$ which is a distance from a certain location to the blade inlet edge on the blade section and the chord length $c$. In the $x$-coordinate, 0 presents the inlet edge and 1 presents the outlet edge. It can be seen from the figure, on the hub streamline, middle streamline and rim streamline, the fluid pressure on the blade pressure surface at the inlet edge is lowest under small flow rate condition, along the direction of fluid flow, the fluid pressure increases gradually and it reaches the largest value near the blade outlet edge. The fluid pressure on the blade suction surface is lower than the pressure surface, and the lowest pressure comes up at the blade inlet edge. The fluid pressure on the blade pressure surface is lowest at the blade inlet edge under design flow rate, along the direction of fluid flow, the fluid pressure increases gradually and it reaches the largest value at the rim of the blade outlet edge. The lowest fluid pressure on the blade suction surface comes up at the middle section near the blade inlet edge where the pressure difference is bigger. Duo to the regional hydraulic shock and flow separation at the blade inlet and outlet under the large flow rate condition, the pressure surface of the blade inlet section appears local low pressure regions where will easily come up cavitation. The fluid pressure on the pressure surface increases rapidly firstly and then increases slowly along the direction of fluid flow. The lowest fluid pressure on the suction surface appears at the middle section near the blade inlet edge, and the maximum pressure appears at the rim of the blade inlet edge. The inverse pressure difference of pressure surface and suction surface at the blade inlet edge is bigger. With the increase of flow rate, the pressure on the blade surface reduces, and the pressure gradient from the inlet edge to the outlet edge slows down gradually.

Fig. 7Pressure distribution on blade surface at the location of different blade height

a) Streamline of the hub

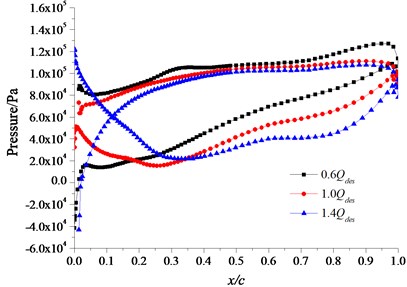
b) Streamline of the middle

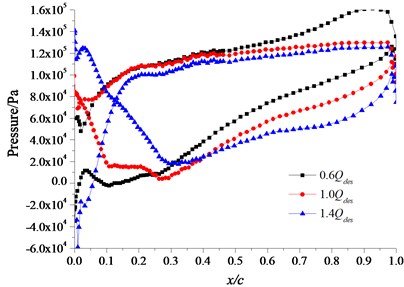
c) Streamline of the rim

4.2. Modal analysis under various working conditions

Fig. 8 shows the static analysis results of the total deformation and equivalent stress of the impeller rotor at the design point based on the steady CFD results, which will be used as the pre-stressing boundary conditions and then conduct the modal analysis. It can be seen from the Fig. 8, the deformation of impeller blade increases from hub to rim and the maximum deformation occur at the blade rim where the maximum deformation is about 0.0611 mm. As the strength for the rest of the impeller is much larger than that of the blade, the deformation is much less than the blade. The stress distribution of impeller blade in the circumferential direction is symmetrical, and the minimum equivalent stress occurs in the region of the rim, but the maximum equivalent stress occurs at the blade outlet edge near the hub. The maximum equivalent stress value is about 22.18 MPa which is far less than the fatigue limit of material and the yield strength. Therefore, the impeller will not take place fatigue damage and plastic deformation. For the traditional strength calculation of impeller makes more simplified, the maximum stress which is calculated with the finite element method is larger than the result of the traditional method.

The results of static analysis under various flow rate conditions are shown in Table 1. Within a certain flow rate range, the maximum stress of the mixed-flow pump impeller decreases and the maximum deformation increases with the increase of flow rate, but the minimum stress decreases firstly and then increases with the increase of the flow rate. When the flow rate is 1.0$Q_{des}$, the minimum stress of impeller appears smaller value, which indicates that the minimum stress of impeller will appear the smallest value under the optimum operating condition.

Fig. 8A distribution diagram of deformation and equivalent stress on impeller

a) Deformation distribution

b) Equivalent stress distribution

The static analysis results are used as the pre-stressing boundary conditions to carry out modal analysis of impeller rotor. As shown in Table 2, it is the modal frequency comparison of first 10 orders in the air and water medium at the design flow rate condition. By comparing the results, there are some differences between natural frequencies of two cases, but the difference is small, and the impact of the blade surface water pressure on the vibration characteristics is very small.

Table 2 shows that the first order frequency of impeller rotor is 1012.5 Hz, and the blade passing frequency (BPF) is 96.6 Hz. Therefore, the natural vibration frequency of mixed-flow pump is much greater than the blade passing frequency which means the resonance will not occur and the fluid-structure coupling calculation is credible.

Table 3 shows the relative difference percentage of natural vibration frequency under different operating condition. The table shows that the natural vibration frequency under different operating condition has some difference, but the difference is not big. The maximum relative difference percentage is 1.003 %, and the minimum relative difference percentage is 0.01 %.

4.3. Deformation of the impeller blades and dynamic stress distribution under the action of fluid-structure interaction

When material or structure undergoes the long-term and repeated dynamic load, although the dynamic stress value does not surpass the material strength limit, the damage might happen still, namely it is the fatigue fracture. Therefore, it is important to improve the operation stability and reliability of impeller rotor by studying the dynamic stress.

Through the above research, the main distribution area of maximum deformation and concentration point of equivalent stress on the blade can be determined. Therefore, four key points are chosen respectively to study in these regions. Fig. 9 is the sampling point location of the equivalent stress. In the figure, point A is located on the rim of blade inlet edge, point B is the intersection between blade inlet edge and hub, point C is the rim of blade outlet edge, and point D is the intersection between blade outlet edge and hub.

Fig. 9Sampling points position of equivalent stress

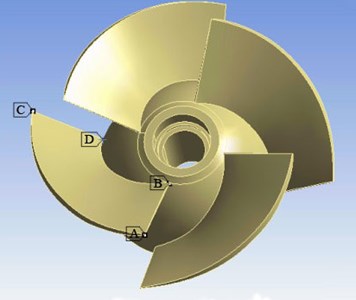
Fig. 10 shows the deformation and equivalent stress distribution on the impeller blade at the design point when $t=$0.16552 s. It can be seen in the Fig. 10(a), the deformation gradient increases obviously from hub to rim in the radial direction and the vibration problem of rim is more outstanding. The maximum deformation occurs at the blade outlet edge on the suction surface near the rim, and the maximum deformation is about 0.0627 mm. The large deformation of the blade rim is mainly because of the magnification of small deformation at the hub, therefore, it is necessary to keep the reasonable clearance between the blade rim and the side wall when designing and checking the pump. As you can see from Fig. 10(b), the maximum equivalent stress occurs at blade outlet edge on the blade suction surface near the hub, where is the most dangerous section of blade and the fatigue fracture is prone to occur, which is basically consistent with the crack location in the engineering practice, and the maximum equivalent stress is about 19.85 MPa. The deformation of the blade is mainly for bending and torsion deformation which caused by the flow field pressure at the impeller outlet edge, and the tensile deformation caused by the centrifugal force is not obvious. It indicates that centrifugal force has little impact on the impeller but the fluid force has greater influence. At the same time, due to the large shock at the blade inlet, when the vibration occurs, the blade inlet edge near the hub could not release stress by elastic deformation. Those will cause stress concentration nearly fulcrum place of blade, namely near the hub, where becomes the distribution area of the maximum equivalent stress. The calculation results of stress concentration can be used as the basis of qualitative analysis, and the stress distribution on the blade surface can be optimized by increasing thickness of blade at hub or taking the circular arc transition way. Comparing the deformation and equivalent stress distribution of impeller with Fig. 7, it can be found that the maximum deformation position and the stress concentration location are basically consistent before and after coupling calculation, but the maximum deformation value increases and the maximum equivalent stress value decreases under the action of fluid-structure interaction. The maximum difference value of deformation is about 0.0016 mm and the maximum difference value of equivalent stress is about 2.33 MPa before and after the coupling calculation. The effect of fluid-structure interaction on the deformation and stress distribution of impeller is obvious, but the maximum equivalent stress is still meeting the requirement of material fatigue limit and yield strength.

Fig. 10A distribution diagram of stress-strain on impeller blade (t= 0.16552 s)

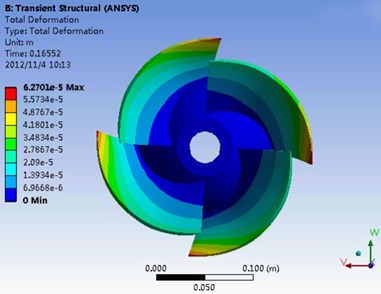
a) Deformation of impeller blade

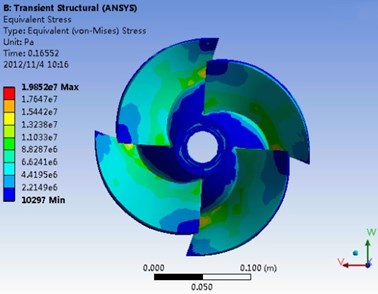
b) Stress distribution of impeller blade

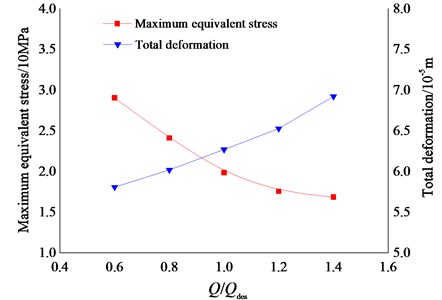
In order to study the effect of flow rate on the maximum equivalent stress and total deformation of impeller, the structural deformation characteristics of the impeller under five different flow conditions (0.6$Q_{des}$, 0.8$Q_{des}$, 1.0$Q_{des}$, 1.2$Q_{des}$, and 1.4$Q_{des}$) are calculated respectively. As shown in Fig. 11, it is the maximum equivalent stress curve and total deformation curve of impeller under different flow rate conditions. It can be seen from the figure, the maximum equivalent stress of the impeller decreases gradually with the increase of flow rate, and the total deformation of the impeller increases gradually with the increase of flow rate.

Fig. 11Curve of maximum equivalent stress and total deformation