Individualized recommending exercises and improving DINA algorithm by CLP-parameter adjustments

1. Introduction

Rapid development on online education all over the world results in a number of platforms, such as EdX, Coursera, Udemy, and Khan Academy, etc. However, the vast amount of data resources may easily lead to the problem of “Overload Information Confuses Choice”. In 1997, Resnick firstly proposed a recommender [1], which has been continuously applied and extended to many fields in industry and commerce, and achieved significantly, such as platforms of Amazon, Google, TikTok, JD.com, and Tencent, as well as many cultural industrial platforms, recommending products or items to customers or users.

In addition, the traditional teaching mode employs indiscriminate teaching and blind training in “the sea of exercises”, and thus increases heavy burden on learners. Most exercise websites select the exercise to recommend from vast amount of online exercises by a single screening configuration, which is essentially an indiscriminate delivery and leads to low learning efficiency and poor targeting. How to accurately recommend appropriate exercises to learners is a hot problem in construction of an intelligence-assisted learning system. Although there have already been a number of researches and achievements in individualized exercises recommendation, including learner and exercise modeling, and recommendation algorithm designing, there are still lots of predicaments, such as difficult representation and insufficient perception on exercise features, difficult diagnosis on learners' status, and difficult definition on the knowledge points dynamically mastered by a learner via exercise-doing, etc. These difficulties then lead to low accuracy of exercises recommendation. The predicaments result in that, even the mostly-concerned DINA algorithm with widely-concerned CDM still has such problems of low accuracy, and inability to time-serially cognize knowledge mastery level and perceive dynamic status of learners and exercises, which are collectively referred to as ‘cognitive level perception (CLP)’ in this paper. In addition, an inherent limitation of current methods is that the implicit connections between learners (exercises) have been largely ignored, so that finer-grained portraits of learners and exercises are not encoded properly, and thus recommendation result may not be sufficient to capture “suitable” preferences and dynamic status for learners [2]. Consequently, there is still no such an assisted learning system that effectively “recommends suitable exercises (items) to learners (customers)” so far, and more R&D works are to be done.

This paper focuses on individualized exercises recommendation algorithm based on CLP. Firstly, an overview and some analysis on relevant researches are conducted. Then, centering on the mostly-concerned DINA algorithm with widely-concerned CDM, an improved model is proposed for individualized exercises recommendation by four adjustments with changeable CLP-parameters, including three steps of implementation in practice. It is reasonable to predict that the proposed model would have better performance in individualized exercises recommendation. This is to be verified by another part of this study.

2. Brief review on individualized recommending exercises

3. Individualized recommending exercises by CDM

The core purpose of both CD and KT is for “assessment on learners’ status”, which was carried out by CTT at early times. To improve the CTT assessment that is not objective enough, IRT came into being and established a model function for student ability and response accuracy, including such parameters as the difficulty, discrimination, and guessing of exercises. For an IRT model, if input learners’ Q&A data and use parameter estimation, then, both parameters of the exercises and the ability values of the learners (scored 0/1) can be obtained. Constant researches have developed more and more extensions to IRT, such as multi-item response theory (MIRT), graded response model, generalized partial credit model, rating scale model, etc. These models can only provide a learner's ability value but cannot represent the specific status of learner's knowledge mastery. Therefore, theory of cognitive diagnosis has been developed, which was added the cognitive attributes, i.e., knowledge points. The commonly-used ones include rule space model (RSM), NIDA model and DINA model [28].

In the field of learner modeling and algorithm designing for individualized exercises recommendation, CDM-based algorithms with their models are widely concerned. The main types of these models include IRT and DINA models, attribute hierarchy model, and neural network CDM. Where, IRT models can be classified further into one-, two-, and three-parameter types, and DINA model is particularly favored due to its superior interpretability of results, with its improved versions including HO-DINA, P-DINA, and G-DINA, etc.[28] For example, M. Q. Liu [29] applied G-DINA model for individualized recommending math-exercises of functions at middle school. Although DINA algorithm has been paid much more attentions, it can only obtain the knowledge mastery level of learners at a single moment and cannot track the changes of learners’ CLP and exercises’ features in a process of certain time series. This is a problem of worth studying [7]. In addition, these CDM-based individualized recommendation algorithms also have lots of problems to different extents, such as “need to improve recommendation accuracy”, “Q-matrix relies on expert or manual design (time-consuming and labor-intensive)”, and “insufficient perception on dynamic changes of learners and exercises”. Researchers are continuously trying to solve these problems. For instance, A. W. Zhou [30] used a neural CDM model to obtain cognitive state level of learners in real time and then select the exercises with suitable difficulty coefficients to recommend. Similar improvements by machine learning optimization on CDM-based algorithms are ongoing all the way. For examples [31], the model of fuzzy cognitive diagnosis (FuzzyCDM), which is an improvement to DINA, introduced fuzzy logic control to achieve a continuous value for the state of knowledge mastery instead of 0/1; Knowledge plus gaming response model (KPGRM), like a neural CDM, broke away from the interaction functions defined by humans in IRT and DINA algorithms, and used a hidden layer to implement the training functions, and thus the cognitive status can be denoted by continuous value, and “knowledge mastery level” can be learned and thus applicable to large sample data.

4. Improving DINA algorithm by four adjustments with changeable CLP-parameters

CDM-based recommendation algorithms and their models have been paid lots of attention in individualized exercises recommendation, as described in Section 3. Where, both IRT and DINA have been widely concerned, and DINA algorithm seems to be the most prospective solution, due to its relative simplicity and superior interpretability on the results of recommendation. However, even for DINA algorithm and its improved versions, there are still three deficiencies as follow:

1) Inability to track learner's knowledge mastery level and perception on exercises within a certain time series, due to insufficient perception on dynamic changes of learners and exercises.

2) Low accuracy of exercise recommendation.

3) Architectural complexity of algorithm model, including those based on machine learning and or optimization.

To make up above deficiencies, here focuses on improvement of simple, easy and understandable DINA algorithm, and proposes a CLP-based solution, which cognizes better the learner's knowledge mastery level and well perceives the dynamic status of exercises within a certain time series, as defined in Section 1. The improvement is carried out by four variable parameters that adjust the two key factors of probability in DINA algorithm to obtain sufficient CLP capability, so as to form an algorithm with changeable parameter-adjusted CLP for the solution. The performances of recommending exercise should be improved.

DINA algorithm is originally to diagnose learners’ knowledge mastery status. It is based on IRT and analyzes the “Q&A” or “exercise-answer” circumstance for multi-choice exercises, from which the status of a learner is deduced. Fig. 1 simply illustrates the framework of original DINA algorithm.

DINA algorithm [32] assumes the learner either fully master the required knowledge points, or randomly guess, when dealing with an exercise, and uses a $Q$-matrix to represent all required knowledge points, $Q=\left[q_{jk}\right]$, $q_{jk}=$1 or 0 denotes that exercise $j$ contains required knowledge point $k$ or not, respectively. Then, for each learner $i$, define a vector of knowledge mastery level, ${\alpha }_i=\left[{\alpha }_{ik}\right]$, ${\alpha }_{ik}=$1 or 0 denotes that learner $i$ masters knowledge point $k$ or not, respectively. Thus, status of of learner $i$ doing exercise $j$ can be represented by:

where, ${\rho }_{ij}=$1 or 0 denotes that learner $i$ does exercise $j$ correctly or incorrectly (at least one knowledge point has not been mastered). Then, under the condition of learner $i$ with knowledge mastery level ${\alpha }_i$, the probability of doing exercise $j$ correctly can be then obtained by conditional probabilistic computation, i.e.:

where, $x_{ij}$ is the scoring of learner $i$ on exercise $j$, which is an entry of Q&A or exercise-answer matrix $X$, $x_{ij}=$1 denotes doing correctly, or $x_{ij}=$0 denotes doing incorrectly; The two key factors, $s_j$ and $g_j$, are called slip factor and guess factor, respectively, which represent the probability of doing exercise $j$ incorrectly in case of learner $i$ has mastered all the required knowledge points, and the probability of guessing exercise $j$ correctly in case of learner $i$ has not mastered all the points, respectively. Therefore, once input all the data of Q&A of learners on exercises, the two factors and knowledge mastery status $\widehat{{\alpha }_i}$ would be obtained by parameter estimation.

Fig. 1DINA algorithm framework

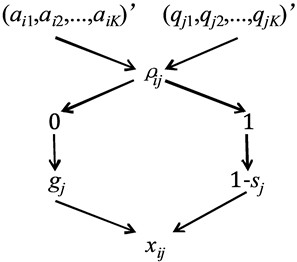
DINA algorithm has the advantages of highly efficient computation and thus capable of processing large-scale data, and providing diagnostic feedback well in detail, however, there is still a limit on its application because of only two states of knowledge mastery level, (0, 1). In addition, in practice, the statuses of both learners and exercises are not so simple - either master all knowledge points’, or “randomly guess with nothing mastered”, which may also be dynamically changed with time being.

To improve the DINA algorithm based on changeable CLP-parameters, which is to be added onto the guess- and slip-factors for learners and exercises, respectively, as shown in Fig. 1:

(1) On Guess factor $g_j$: Consider that, the better the learner is, the greater the probability of guessing correctly without mastering all knowledge points. Therefore, add an variable parameter of individual aim of learner $i$ at current time serial $n$, $A_{in}$, e.g., 1 – higher, or 0 – lower than last time. In addition, add another variable parameter of individual attitude of learner $i$ at current time serial $n$, $B_{in}$, e.g., 1 – carefully, or 0 – halfheartedly doing exercises.

(2) On Slip factor $s_j$: Consider that, the more difficult an exercise is, the greater the probability of doing incorrectly under the condition of mastering all the knowledge points. Therefore, add a variable parameter of exercise-difficulty, $D_{ijn}=d_{0j}{d}_{ijn}$, onto the factor $s_j$. Where, $d_{0j}$ denotes the absolute or constant difficulty with continuous values from 0 – easy to 1 – most difficult, which can be marked by expert(s) in the field, and $d_{ijn}$ denotes the relative/variable difficulty of learner $i$ on exercise $j$, with discrete values 0 – doing correctly and 1 – doing incorrectly, at current time serial number $n$. In addition, add another parameter of exercise-classification, $C_{ijn}=c_{0j}{c}_{ijn}$, where, $c_{0j}$ denotes absolute or constant classification marked by expert(s) in the field, representing the category or special labeled set of exercise $j$, and $c_{ijn}$ denotes relative or variable classification, 1 – to recommend, or 0 – not to recommend, after the time serial number $n$.

In summary, the adjustments on the two factors by use of four variable parameters can be schemed in following way:

where, mark ‘$\otimes$’ denotes some sort of mathematical operation(s) to be predetermined by simulations and or experiments. Actually, except for the four variable parameters ($A_{in}$, $B_{in}$, $C_{ijn}$, $D_{ijn}$), there may be some other variable parameters to be used for the adjustments, such as the representations of non-structural latent features of “memory and or forgetting” curves or factors of learners. Fig. 2 shows the overall architecture.

Fig. 2Architecture of improving DINA algorithm

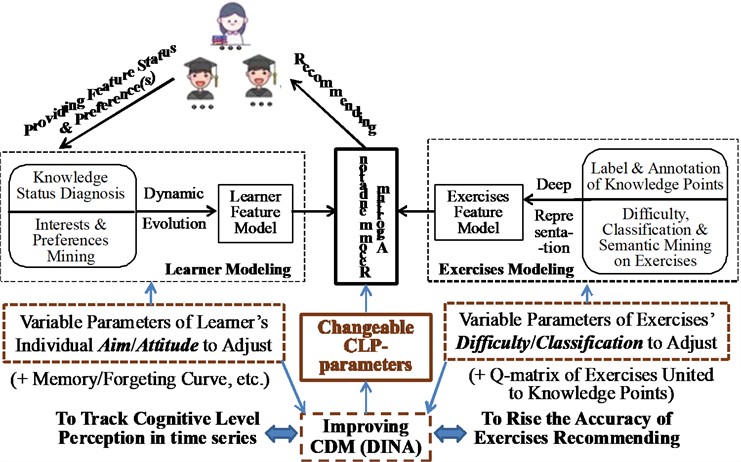
The proposed model is implemented by the following three primary steps, which can also be referred to see in Fig. 2.

Step 1: Fix the “learner-answer scoring matrix $X={\left[x_{ij}\right]}_{I\times J}$” and “exercise-knowledge point matrix $Q={\left[q_{jk}\right]}_{J\times K}$”, which can be fixed by an initial test (or prior) answering scores’ record and expert in the field, respectively, at cold start.

Step 2: Maximize the edge likelihood of conditional probability ${P_j\left({x_{ij}=1|\alpha }_i\right)\mathrm{}}_{VPA}$ in Eq. (3) to obtain the factors’ estimates (${{\widehat{s}}_j,\widehat{g}}_j$) of $\left(s_j,g_j\right)$ by expectation maximization (EM) algorithm. And the optimal estimate of knowledge-point mastery vector, $\widehat{{\alpha }_i}$, can be obtained by maximize the posterior probability of scoring matrix $X$ [23] as:

Step 3: Once the factors’ estimates (${{\widehat{s}}_j,\widehat{g}}_j$) and the optimal estimate ${\widehat{a}}_i$ have been obtained, put them back into Eq. (1) to compute ${\rho }_{ij}$, and then put them into Eq. (3) to compute the ${P_j\left({x_{ij}=1|\alpha }_i\right)\mathrm{}}_{VPA}$, in terms of which the Top-N probabilities can be listed, correspondingly, the exercises’ list ($j=1,\dots ,N$) are supposed to be recommended to learner $i$.

It is reasonable to predict that, whole performance of the proposed improved DINA algorithm would be better via the above steps of implementation than that of original DINA algorithm, including recommendation accuracy. Simulation and experimental verification on the performances will be carried out in the next part of this study.

5. Conclusions

Individualized exercises recommendation is essentially an important part of adaptive learning systems. It plays a significant role in consolidating learners’ knowledge points, diagnosing their cognitive statuses and or levels. Recommending exercises suitable for learners’ cognitive levels and abilities could stimulate and cultivate their learning motivation, and improve their learning enthusiasm and persistence. Although existing research on the theory and application of individualized exercises recommendation have obtained a certain achievements and effects, there are still many challenges in practice on next three critical areas:

1) In exercise modeling, how to further achieve deep semantic representation of cross-modal exercises, deeply mine exercise features, and use such generative AI-technology as ChatGPT for in-depth semantic annotation, thereby reduce manual annotation and improve modeling efficiency, are all to be studied. Additionally, some exercise-features may change with dynamic status of learners, how to synchronously perceive and represent this dynamism and embed them into the corresponding algorithm is also a problem worth studying.

2) In learner modeling, how to establish a theoretical system with multi-dimensional ability of cognitive diagnosis is to be investigated to combine static and dynamic learning-status perceptions.

3) In exercises recommendation algorithm, how to ensure the interpretability, meanwhile, further improve the accuracy of recommendation is always an ongoing target.

These problems and challenges are to be well faced with much efforts. Constructing a practically efficient individualized exercises recommender still need more in-depth investigations and effective works.

Centering at CDM-based individualized exercises recommendation, this study has proposed a solution model with changeable CLP-based algorithm, together with three steps of implementation. It is reasonable to predict that, whole performance of the proposed model would become better than that of DINA algorithm, including recommendation accuracy, due to better CLP on both static and dynamic changes of learners and exercises. These will be conducted and verified by another part work of this study.