Bending of a piecewise homogeneous plate with a circular interfacial materials separation zone and radial crack considering the strip contact of its edges

Slobodian, Mykola; Zvizlo, Ivan; Bilash, Oksana; Sorokatyi, Mykola; Petruchenko, Oksana; Markevych, Lukiian

doi:10.21595/vp.2024.24515

Vibroengineering Procedia

Browse Procedia

Published: 27 September 2024

Check for updates

Bending of a piecewise homogeneous plate with a circular interfacial materials separation zone and radial crack considering the strip contact of its edges

Mykola Slobodian¹

Ivan Zvizlo²

Oksana Bilash³

Mykola Sorokatyi⁴

Oksana Petruchenko⁵

Lukiian Markevych⁶

^{1, 2, 6}Department of Mechanics, Faculty of Mechanics and Mathematics, Ivan Franko National University of Lviv, Lviv, Ukraine

^{3, 4}Department of Engineering Mechanics (Weapons and Equipment of Military Engineering Forces), Faculty of Support Forces, Hetman Petro Sahaidachnyi National Army Academy, Lviv, Ukraine

⁵Scientific Research Institute, Yuri Illenka Street, Kyiv, Ukraine

Corresponding Author:

Oksana Bilash

Cite the article Download PDF

Downloads 23

Abstract

The work presents a solution to the bending problem of an infinite piecewise homogeneous isotropic plate with an elastic circular washer and a radial through straight crack. It was assumed that under the action of an external loads at infinity, the edges of the crack are smoothly contacted on area of constant width (strip contact) on the upper base of the plate. The solution of the problem is built using the methods of the theory of functions of a complex variable and complex potentials and is reduced to a system of singular integral equations, which is numerically solved using the method of mechanical quadrature A numerical analysis of the problem is conducted and graphic dependencies of contact force, coefficients of intensity of moments and forces at various parameters of the problem were constructed.

1. Introduction

Lamellar structural elements are widely used in various fields of engineering. They may contain finite inclusions of a technological nature and during operation, cracks may appear in such elements, abruptly reducing the permissible load level that the structure can withstand. It is clear from the physical considerations that, under the conditions of plate bending, the crack edges will be in contact. Therefore, from scientific and technical task of mechanics it is relevant to develope methods that determine the stress-strain state of plates with cracks which edges are in contact during bending. One of the main tasks in assessing the strength of a structural element with cracks is to determine the coefficients of the intensity of forces and moments, which are used to characterize the stress-strain state around the crack peaks, as well as to determine the critical load that can be applied to the plate.

Research on the stress-strain state of plates with cracks during bending using the Kirchhoff-Love theory is given in [1-4]. In these works, it was assumed that the edges of the crack are in contact along the entire length on the upper or lower base of the plate. Kalthoff J. F., Shatsky I. P., Bürgel A. [5] experimentally investigated the contact of crack edges during the bending of a plate and confirmed the presence of a membrane component of the stress field near the crack, which is a direct consequence of the contact interaction of the crack edges during the bending of the plate.

In the work of J. P. Dempsey, I. I. Shekhtman, and L. I. Slepyan [6], the problem of bending a plate with a through crack, where the edges of the crack are in contact over the height of the plate, was the first time analytically solved. The bending of a circular plate with a system of through straight cracks, the edges of which are in contact over the height of the plate, is considered in [7]. The stress-strain state of a plate with a crack, the edges of which are in contact under the action of external load, and on the continuation of which plastic zones were formed, was investigated in works [8, 9]. The study of the stress-strain state of bodies with interphase cracks with contact zones was carried out in works [10, 11]. The influence of the contact of the edges of a thermoisolated interfacial crack under thermomechanical loading on the stress-strain state was studied in [12]. The stress-strain state of a beam with a crack, the edges of which are in contact and on the continuation of which a plastic zone was formed, was investigated in [13]. Therefore, problems of bending plates with a system of cracks, the edges of which are in contact, are relevant. The work formulates a model of the smooth contact of the crack edges on area of constant width for the bending problem of a piecewise homogeneous plate. This model makes it possible to estimate more accurately the influence of a crack on the stress-strain state of the plate and on its strength.

2. Problem statement

Consider an infinite piecewise homogeneous isotropic plate of thickness $2 h$ with a circular interfacial materials separation zone of radius $R$ and a radial crack of length $2 l$ , which is free from external loading. It is assumed that under the action of bending moments at infinity (Fig. 1(a)) the edges of the crack come into smooth contact along the region of constant width (strip contact) on the upper base of the plate (Fig. 1(b)).

Fig. 1a) The scheme of the plate loading and crack placement and b) the scheme of the crack edge contact

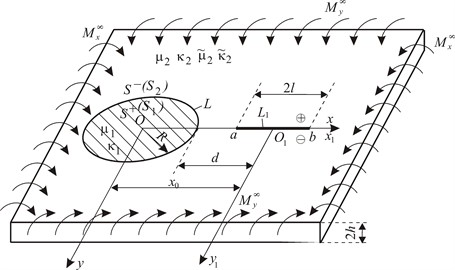
a)

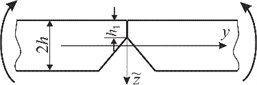
b)

In the middle plane of the plate, we choose a Cartesian coordinate system $O x y \tilde{z}$ , directing the axis $O \tilde{z}$ perpendicular to it, and the origin of the coordinates $O$ coincides with the center of the circular washer, and the crack located along the $O x$ . Additionally, in this plane, we introduce a polar coordinate system $r$ and $θ$ with the pole at the point $O$ and the polar axis along the $O x$ . We assume that the center of the crack has the coordinate $x_{0}$ , where $x_{0} > R + l$ . We associate a Cartesian coordinate system $O_{1} x_{1} y_{1}$ with the crack. Quantities related to the washer will be denoted with index 1, and those related to the matrix with index 2. The points of the plane $O x y$ , coinciding with the crack ends will be denoted by $a$ and $b$ , the area in the middle of the circular tough washer – as $S^{+}$ $(S_{1})$ , outside – as $S^{-}$ $(S_{2})$ , the line where the crack is located – as $L_{1}$ , and the separation boundary of materials – by $L$ . The distributed bending moments at infinity are denoted by $M_{x}^{\infty}$ and $M_{y}^{\infty}$ (Fig. 1(a)).

Due to the contact of the crack edges, the solution to the problem will be sought in the form of solutions of two interrelated problems: the problem of plate bending (classical plate bending theory) and the plane problem of elasticity theory under the following boundary conditions:

1

σ_{y_{1} y_{1}}^{\pm} = \frac{- N}{(2 h)}, σ_{x_{1} y_{1}}^{\pm} = 0, P^{\pm} = 0, \partial_{x_{1}} [u_{Π 1}] + α h [\partial_{x_{1} y_{1}}^{2} w] = 0,

M_{y_{1}}^{\pm} = β h N, x_{1} \in L_{1},

2

P_{r 1} = P_{r 2}, M_{r 1} = M_{r 2}, u_{r 1} = u_{r 2}, u_{θ 1} = u_{θ 2}, w_{1} = w_{2}, \partial_{r} w_{1} = \partial_{r} w_{2}, x \in L,

where $α = 0,5 \cdot (1 + {(1 - γ)}^{2})$ , $β = 1 - γ / 3$ , $γ = h_{1} / h$ , $N -$ contact force between the edges of the crack; $σ_{x_{1} y_{1}}$ , $σ_{y_{1} y_{1}}$ – components of the stress tensor, $u_{r j}$ and $u_{θ j}$ , $u_{Π 1}$ – components of the displacement vector in the plane problem; here and henceforth, the index $j$ takes two values: 1 and 2; $w_{j}$ – deflection of the plate, $M_{r j}$ , $M_{y_{1}}$ – bending moments, $P_{y_{1}}$ , $P_{r j}$ – shearing force generalized in the sense of Kirchhoff; $[f] = f^{+} - f^{-}$ , the “+” and “–” signs indicate the boundary values of the function when the point of the plane approaches the crack at $y_{1} \to \pm 0$ , $\partial_{x} f = \partial f / \partial x$ .

3. Solution

Using the complex potentials of the plane problem and the plate bending problem [14], satisfying the boundary conditions Eqs. (1)-(2), the solution of the problem is reduced to linear conjugation problems, based on which a system of singular integral equations is obtained for the unknown displacement jumps $G_{j} (η)$ and rotation angle jumps $Y_{j} (η)$ on the crack edges, which takes the form:

3

i \cdot \int_{- 1}^{1} \{Y_{1} (η) \cdot K (η, ξ) + \bar{Y_{1} (η)} \cdot L (η, ξ)\} d η = i \tilde{c^{'}} + \tilde{m} \cdot \frac{β h N}{M_{y}^{\infty}} + P (ξ), ξ \in [- 1, 1],

4

\int_{- 1}^{1} \{G_{1} (η) \cdot R (η, ξ) + \bar{G_{1} (η)} \cdot S (η, ξ)\} d η = \frac{- 0,5 π \cdot h N}{M_{y}^{\infty}}, ξ \in [- 1, 1],

where:

K (η, ξ) = - \frac{1}{π} \{\frac{{\tilde{κ}}_{2}}{η - ξ} + \frac{λ}{2} \{\{\tilde{g} {\tilde{A}}_{4} (1 + \frac{1}{X^{2}}) + (\tilde{a} - {\tilde{A}}_{5} {\tilde{A}}_{13}) \frac{1}{2 X^{2}}\} \frac{1}{T}

+ \frac{1}{T X - 1} \{\tilde{g} {\tilde{A}}_{4} (\frac{{\tilde{κ}}^{2}}{X} - X - \frac{3}{X^{3}}) - \frac{{\tilde{A}}_{3}}{\tilde{g} X}\}

+ \frac{\tilde{g} {\tilde{A}}_{4}}{{(T X - 1)}^{2}} (X + \frac{4}{X} - \frac{5}{X^{3}}) - \frac{2 \tilde{g} {\tilde{A}}_{4}}{X} (X - \frac{1}{X}) \frac{1}{{(T X - 1)}^{3}}\}\},

L (η, ξ) = - \frac{λ}{2 π} \{\frac{1}{T} ({\tilde{κ}}_{2} \tilde{g} {\tilde{A}}_{4} - \frac{1}{X^{2}} ({\tilde{A}}_{4} - \frac{\tilde{a}}{2} + \frac{{\tilde{A}}_{5} {\tilde{A}}_{13}}{2})) + \frac{{\tilde{κ}}_{2} \tilde{g} {\tilde{A}}_{4}}{T X - 1} (\frac{3}{X^{3}} - X - \frac{2}{X})

+ \frac{{\tilde{κ}}_{2} \tilde{g} {\tilde{A}}_{4}}{{(T X - 1)}^{2}} (X + \frac{1}{X^{3}} - \frac{2}{X})\},

P (ξ) = - \tilde{m} + \tilde{g} {\tilde{A}}_{4} \frac{B^{'}}{X^{2}} ({\tilde{κ}}_{2} + 1 - \frac{3}{X^{2}}) - 2 {\tilde{A}}_{13} \frac{A}{X^{2}},

R (η, ξ) = \frac{1}{η - ξ} - \frac{λ g A_{4}}{2 (T X - 1)} \{\frac{1}{X} - (\frac{1}{X^{2}} + 1) \{X + \frac{1}{X} - (X - \frac{1}{X}) \frac{1}{T X - 1}\}

+ (X - \frac{1}{X}) \{\frac{4}{X^{2}} \frac{1}{T X - 1} + \frac{2}{X^{2}} - \frac{2}{X} (X - \frac{1}{X}) \frac{1}{{(T X - 1)}^{2}}\}\} + \frac{λ g^{- 1} A_{3}}{2 X (T X - 1)} + \frac{λ A_{4}}{2 T} (\frac{B_{8}}{X^{2}} - g),

S (η, ξ) = - \frac{λ}{2} \{\frac{1}{T} (\frac{B_{9}}{X^{2}} + g A_{4}) - \frac{g A_{4}}{T X - 1} \{X - \frac{1}{X^{3}} - (X - \frac{1}{X}) \frac{1}{T X - 1} + \frac{1}{X^{2}} (\frac{1}{T X - 1} + 2)\}\},

Y_{1} (t) = \frac{Q_{2} Q (t)}{M_{y}^{\infty}} = Y_{11} (t) + i Y_{12} (t), G_{1} (t) = - i h^{2} (M_{y}^{\infty})^{- 1} g^{'} (l η) = G_{11} (η) + i G_{12} (η),

Q_{j} = E_{j} h^{3}, D_{j} = 2 Q_{j} {(3 (1 - υ_{j}^{2}))}^{- 1}, \tilde{m} = - {({\tilde{D}}_{2} (1 - υ_{2}))}^{- 1}, {\tilde{D}}_{2} = 2 {(3 (1 - υ_{2}^{2}))}^{- 1},

{\tilde{κ}}_{j} = \frac{(3 + υ_{j})}{(1 - υ_{j})}, B = - \frac{1 - ρ}{2} \tilde{m}, μ_{j} = \frac{E_{j}}{(2 (1 + υ_{j}))}, κ_{j} = \frac{(3 - υ_{j})}{(1 + υ_{j})},

{\tilde{μ}}_{j} = \frac{1}{D_{j} (1 - υ_{j})}, A = - \frac{ρ + 1}{4 {\tilde{D}}_{2} (1 + υ_{2})}, ρ = \frac{M_{x}^{\infty}}{M_{y}^{\infty}},

{\tilde{B'}}_{1} = 0, {\tilde{B'}}_{0} = - {\bar{\tilde{A}'}}_{0}, {\tilde{A}}_{j} = {\tilde{μ}}_{j} + {\tilde{μ}}_{3 - j} {\tilde{κ}}_{j}, \tilde{g} = - {\tilde{A}}_{1} {\tilde{A}}_{2}^{- 1},

{\underline{A A}}_{3} = {\tilde{μ}}_{1} {\tilde{κ}}_{2} - {\tilde{μ}}_{2} {\tilde{κ}}_{1}, {\underline{A A}}_{4} = {\tilde{μ}}_{2} - {\tilde{μ}}_{1}, {\tilde{A}}_{4} = {\underline{A A}}_{4} {\tilde{A}}_{1}^{- 1}, {\tilde{A}}_{3} = {\underline{A A}}_{3} {\tilde{A}}_{2}^{- 1},

{\tilde{A}}_{5} = {\tilde{μ}}_{2} (1 + {\tilde{κ}}_{1}) {\tilde{A}}_{1}^{- 1}, {\tilde{A}}_{12} = {\tilde{A}}_{4} - {\tilde{g}}^{- 1} {\tilde{A}}_{3}, \tilde{a} = {\tilde{A}}_{3} {\tilde{g}}^{- 1} + {\tilde{A}}_{4}, {\tilde{A}}_{13} = {\tilde{A}}_{12} / (1 - {\tilde{A}}_{4})

B_{8} = A_{5} (g^{- 1} A_{3} - 1) A_{6}, B_{9} = A_{4} + A_{5} ({A_{4}}^{2} - g^{- 1} A_{. 3}) A_{6}, B_{5} = μ_{2} (1 + κ_{2}) A_{1}^{- 1},

{\tilde{A}}_{3} = μ_{1} κ_{2} - μ_{2} κ_{1}, A {\tilde{A}}_{4} = μ_{2} - μ_{1}, g = - A_{a} {A_{2}}^{- 1}, A_{3} = A {\tilde{A}}_{3} A_{2}^{- 1}, A_{4} = A {\tilde{A}}_{4} A_{1}^{- 1}

A A_{j} = μ_{j} + μ_{3 - j} κ_{j}, A_{6} = {(1 - A_{4}^{2})}^{- 1}, B_{8} = A_{5} (g^{- 1} A_{3} - 1) A_{6},

B_{9} = A_{4} + A_{5} ({A_{4}}^{2} - g^{- 1} A_{. 3}) A_{6}, B_{5} = μ_{2} (1 + κ_{2}) A_{1}^{- 1}, T = {\tilde{X}}_{0} + λ η, X = {\tilde{X}}_{0} + λ ξ,

where $E_{j}$ – Young’s modulus, $υ_{j}$ – Poisson’s ratios; $Y_{11} (t)$ , $Y_{12} (t)$ , $G_{11} (t)$ and $G_{12} (t)$ – real functions.

To the Eqs. (3), (4) we add additional conditions:

5

\int_{- 1}^{1} Y_{1} (η) d η = 0, \int_{- 1}^{1} η Y_{11} (η) d η = 0, \int_{- 1}^{1} G_{1} (η) d η = 0,

which express respectively single-valued rotational angles and deflection of the plate when bypassing the contour of each crack.

From the boundary Eq. (1), we obtain:

6

G_{11} (η) + \frac{α (1 + {\tilde{κ}}_{2})}{(1 + κ_{2}) (1 + υ_{2})} Y_{12} (η) = 0, η \in [- 1, 1] .

Thus, to determine the unknown functions $Y_{1} (η)$ and $G_{1} (η)$ we have a system of integral Eqs. (3)-(6).

4. Numerical analysis and conclusions

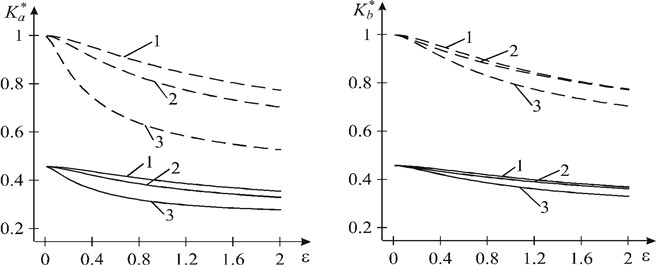
A numerical analysis of the problem was carried out, which is presented in Fig. 2-4 at $υ_{1} = υ_{2} = 0.3$ , $γ = 0.13$ . It should be noted, that the consolidated coefficients of the intensity of forces $K_{N}^{*} = K_{N} / (M_{y}^{\infty} \sqrt{l})$ and moments $K_{M}^{*} = K_{M} / (M_{y}^{\infty} \sqrt{l})$ are related by the dependence $K_{N}^{*} / K_{M}^{*} = 3 α (1 + υ_{2}) / (3 + υ_{2})$ , therefore, we do not provide graphical dependencies for $K_{N}^{*}$ .

Fig. 2a illustrates graphical dependence of the consolidated contact force between the edges of the crack $N^{*} = h N / M_{y}^{\infty}$ on the consolidated coordinate $ξ = x_{1} / R$ for $\tilde{n} = E_{1} / E_{2} = 0.1$ , $ρ = M_{x}^{\infty} / M_{y}^{\infty} = 1$ , $R = l$ . Curve 1 is obtained at $ε = λ = 1 / 1.1$ ( $ε = R / d$ , $λ = l / d$ ), curve 2 – at $ε = λ = 1 / 1.2$ , curve 3 – at $ε = λ = 1 / 1.5$ , curve 4 – at $ε = λ = 1 / 2$ , curve 5 – at $ε = λ = 0$ . As we can see from this figure, as the crack approaches the circular boundary, the magnitude of the contact force $N^{*}$ between the edges of the crack increases compared to an isolated crack, and for the peak closer to the washer $a$ $(ξ = - 1)$ it is larger than farther from the hole $b$ $(ξ = 1)$ .

Fig. 2Graphical dependence of the consolidated contact force between the edges of the crack

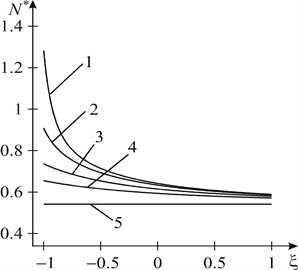
a)

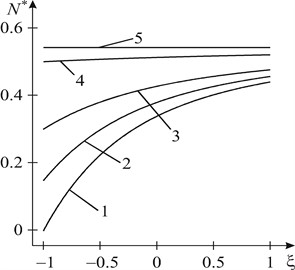
b)

Fig. 3 and Fig. 4 shows the graphical dependence for coefficients of the intensity of moments at vertices a and b on $ε = R / d$ at $\tilde{n} = E_{1} / E_{2} = 0.1$ and $\tilde{n} = E_{1} / E_{2} = 10$ respectively, when $ρ = M_{x}^{\infty} / M_{y}^{\infty} = 1$ . Solid lines represent the curves for coefficients of the intensity of moments, obtained, taking into account the contact of the crack edges, dashed lines – without considering the contact between the crack edges. Curves 1 are constructed at $λ = l / d = 0.2$ , curves 2 – at $λ = 0.5$ , curves 3 – at $λ = 0.8$ . As can be seen from Fig. 4 when $\tilde{n} = E_{1} / E_{2} = 0.1$ coefficients of the intensity of moments increases with the increase of the relative radius $ε = R / d$ of the circular interfacial materials separation zone, but at $\tilde{n} = E_{1} / E_{2} = 10$ (Fig. 4) coefficients of the intensity of moments with the same parameters of the problem decrease with the increase of $ε = R / d$ .

Fig. 3Graphical dependence of the consolidated coefficients of the intensity of moments on ε for n~=0.1

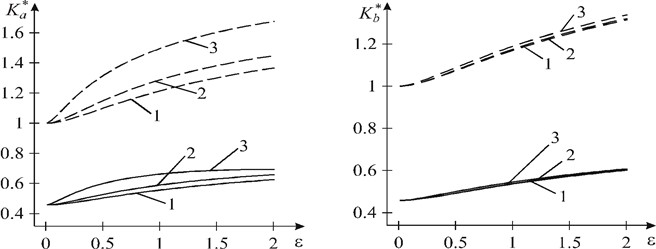
Fig. 4Graphical dependence of the consolidated coefficients of the intensity of moments on ε for n~=10

References

I. P. Shatsky, “Bending of a plate weakened by a cut with contacting edges,” (in Ukrainian), Doklady Akademii Nauk SSSR, Vol. 7, pp. 49–51, 1988.

Search CrossRef
T. M. Dalyak and I. P. Shatskyi, “Interference of closable cracks and narrow slits in an elastic plate under bending,” Journal of the Serbian Society for Computational Mechanics, Vol. 14, No. 2, pp. 51–68, Dec. 2020, https://doi.org/10.24874/jsscm.2020.14.02.04

Publisher
I. Shatskyi and T. Dalyak, “Interaction of contact cracks and narrow slits in plate bending,” Procedia Structural Integrity, Vol. 13, pp. 1476–1481, Jan. 2018, https://doi.org/10.1016/j.prostr.2018.12.304

Publisher
M. J. Young and C. T. Sun, “Influence of crack closure on the stress intensity factor in bending plates? A classical plate solution,” International Journal of Fracture, Vol. 55, No. 1, pp. 81–93, May 1992, https://doi.org/10.1007/bf00018034

Publisher
J. F. Kalthoff, I. P. Shatsky, and A. Bürgel, “Experimental confirmation of the contact of crack interfaces during plate bending,” (in Ukrainian) in Fracture Mechanics of Materials and Structural Integrity, Vol. 1, Lviv: Kamenyar, 1999, pp. 72–74.

Search CrossRef
J. P. Dempsey, I. I. Shekhtman, and L. I. Slepyan, “Closure of a through crack in a plate under bending,” International Journal of Solids and Structures, Vol. 35, No. 31-32, pp. 4077–4089, Nov. 1998, https://doi.org/10.1016/s0020-7683(97)00302-8

Publisher
M. S. Slobodian and M. I. Shainoga, “Stress-strain state of bent plate with system of cracks with faces contacting within constant-height zone,” International Applied Mechanics, Vol. 60, No. 2, pp. 188–202, Jul. 2024, https://doi.org/10.1007/s10778-024-01273-x

Publisher
V. K. Opanasovych and M. S. Slobodyan, “Biaxial bending of an isotropic plate with through rectilinear crack with regard for the width of the contact zone of its edges and in the presence of plastic zones near its tips,” Journal of Mathematical Sciences, Vol. 228, No. 2, pp. 162–172, Nov. 2017, https://doi.org/10.1007/s10958-017-3613-z

Publisher
V. K. Opanasovych, Nykolyshyn, M. S. Slobodian, S. O. Alfavitska, and O. K. Bilash, “Combined action of bending and tension of an isotropic plate with through crack in the absence of contact between the faces and with regard for the plastic zones and hardening of material at the tips,” Journal of Mathematical Sciences, Vol. 254, No. 1, pp. 117–128, Mar. 2021, https://doi.org/10.1007/s10958-021-05292-8

Publisher
V. J. Adlucky and V. V. Loboda, “Finite-element analysis of the elastoplastic state of a plane with elliptic inclusion in the presence of interface crack,” Journal of Mathematical Sciences, Vol. 270, No. 1, pp. 76–86, Mar. 2023, https://doi.org/10.1007/s10958-023-06333-0

Publisher
V. Loboda, A. Sheveleva, and O. Mykhail, “A slipping zone model for a conducting interface crack in a piezoelectric bimaterial,” in Mechanics and Physics of Structured Media, Elsevier, 2022, pp. 253–269, https://doi.org/10.1016/b978-0-32-390543-5.00018-9

Publisher
K. I. Serednytska and R. M. Martynyak, “Contact of the faces of an interface thermally insulated crack under thermomechanical loading,” Materials Science, Vol. 57, No. 2, pp. 173–179, Jan. 2022, https://doi.org/10.1007/s11003-021-00528-z

Publisher
O. Bilash, M. Slobodian, R. Seliverstov, I. Zvizlo, O. Petruchenko, and R. Kovalchuk, “Pure bending of a strip (Beam) with a transversal through crack located asymmetrically relative to its axis on the assumption of crack closure and striplike plastic zone near one of the tips,” in International Scientific Session on Applied Mechanics XI: Proceedings of the 11th International Conference on Applied Mechanics, Vol. 2949, p. 020002, Jan. 2023, https://doi.org/10.1063/5.0165477

Publisher
I. A. Prusov, Method of Conjugation in the Theory of Plates. (in Russian), Minsk: BSU, 1975.

Search CrossRef

About this article

Received

30 August 2024

Accepted

24 September 2024

Published

27 September 2024

SUBJECTS

Mechanical vibrations and applications

DOI

https://doi.org/10.21595/vp.2024.24515

Keywords

plate

crack

closure

plane problem

bending

linear conjugation

singular equations

contact force

Acknowledgements

The authors have not disclosed any funding.

Data Availability

The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

Conflict of interest

The authors declare that they have no conflict of interest.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2023 12 30

A third-order shear deformation plate bending formulation for thick plates: first principles derivation and applications

Charles Chinwuba Ike

Research article

2020 11 26

Mathematical modeling of the solution to the problem of plate bending given various fastenings along the contour and various loads

Serikbay Toibayev, Assemgul Uderbayeva, Zhanar Bidakhmet, Ayaulym Rakhmatulina, Algazy Zhauyt

Research article

2020 11 26

Bending of a circular flexible plate taking into account the initial curvature

G. U. Mamatova, А. K. Sugirbekova, N. M. Bekaulov

Research article

2018 06 30

Mathematical solutions for the flexural analysis of Mindlin’s first order shear deformable circular plates

Charles Chinwuba Ike

M. Slobodian, I. Zvizlo, O. Bilash, M. Sorokatyi, O. Petruchenko, and L. Markevych, “Bending of a piecewise homogeneous plate with a circular interfacial materials separation zone and radial crack considering the strip contact of its edges,” Vibroengineering Procedia, Vol. 55, pp. 54–59, Sep. 2024, https://doi.org/10.21595/vp.2024.24515

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/vp.2024.24515
UR  - https://doi.org/10.21595/vp.2024.24515
TI  - Bending of a piecewise homogeneous plate with a circular interfacial materials separation zone and radial crack considering the strip contact of its edges
T2  - Vibroengineering Procedia
AU  - Slobodian, Mykola
AU  - Zvizlo, Ivan
AU  - Bilash, Oksana
AU  - Sorokatyi, Mykola
AU  - Petruchenko, Oksana
AU  - Markevych, Lukiian
PY  - 2024
DA  - 2024/09/27
PB  - Extrica
SP  - 54-59
VL  - 55
SN  - 2345-0533
SN  - 2538-8479
ER  - 

Copy Ris

Copied to clipboard!

 @article{Slobodian_2024, title={Bending of a piecewise homogeneous plate with a circular interfacial materials separation zone and radial crack considering the strip contact of its edges}, volume={55}, ISSN={2538-8479}, url={https://doi.org/10.21595/vp.2024.24515}, DOI={10.21595/vp.2024.24515}, journal={Vibroengineering Procedia}, publisher={JVE International Ltd.}, author={Slobodian, Mykola and Zvizlo, Ivan and Bilash, Oksana and Sorokatyi, Mykola and Petruchenko, Oksana and Markevych, Lukiian}, year={2024}, month=sep, pages={54–59} }

Copy Bibtex

Copied to clipboard!

[1]M. Slobodian, I. Zvizlo, O. Bilash, M. Sorokatyi, O. Petruchenko, and L. Markevych, “Bending of a piecewise homogeneous plate with a circular interfacial materials separation zone and radial crack considering the strip contact of its edges,” Vibroengineering Procedia, vol. 55, pp. 54–59, Sep. 2024, doi: 10.21595/vp.2024.24515.

Copy IEEE

Copied to clipboard!

Slobodian, Mykola, Ivan Zvizlo, Oksana Bilash, Mykola Sorokatyi, Oksana Petruchenko, and Lukiian Markevych. “Bending of a Piecewise Homogeneous Plate with a Circular Interfacial Materials Separation Zone and Radial Crack Considering the Strip Contact of Its Edges.” Vibroengineering Procedia 55 (September 27, 2024): 54–59. https://doi.org/10.21595/vp.2024.24515.

Copy Chicago

Copied to clipboard!

Bending of a piecewise homogeneous plate with a circular interfacial materials separation zone and radial crack considering the strip contact of its edges

Abstract

1. Introduction

2. Problem statement

3. Solution

4. Numerical analysis and conclusions

References

About this article

Related Articles