Estimation of vehicle state based on maximum correntropy square-root cubature Kalman Filter

Liu, Yingjie; Cui, Dawei

doi:10.21595/jme.2024.24376

Journal of Measurements in Engineering

Browse Journal

Submit article

Published: 02 January 2025

Check for updates

Estimation of vehicle state based on maximum correntropy square-root cubature Kalman Filter

Yingjie Liu¹

Dawei Cui²

¹Huzhou Key Laboratory of Urban Multidimensional Perception and Intelligent Computing, Huzhou, 313000, P. R. China

^{1, 2}School of Machinery and Automation, Weifang University, Weifang, 261061, Shandong, China

Corresponding Author:

Yingjie Liu

Cite the article Download PDF

Article in Press

Downloads 27

Abstract

State estimation of a vehicle is an important direction under the research branch of automotive dynamics, with the aim of determining state variables that reflect vehicle handling stability and other characteristics. In order to solve the problem of poor estimation accuracy caused by heavy tailed non Gaussian noise in traditional state estimation methods, a new filtering algorithm based on the Maximum Correlation Entropy criterion (MCC) and the Square-root Cubature Kalman Filter (MCSCKF) is proposed. On the basis of establishing a nonlinear 3-DOF vehicle model, the yaw rate and the side slip angle as well as the longitudinal velocity of the vehicle were estimated. And the effectiveness of the algorithm was verified through joint simulation with Carsim and Matlab/Simulink. The results show that the MCSCKF algorithm can adapt to complex working conditions and has better accuracy in vehicle state estimation than traditional state estimation algorithms. Meanwhile, the MCSCKF algorithm can effectively reduce the impact of heavy tail non Gaussian noise and improve the accuracy of vehicle state estimation.

Estimation of vehicle state based on maximum correntropy square-root cubature Kalman Filter

Highlights

The MCSCKF algorithm can adapt to complex working conditions and has better accuracy in vehicle state estimation than traditional state estimation algorithms.
The proposed MCSCKF algorithm can solve the problem of vehicle state estimation with the performance of noise fluctuation suppression and higher estimation accuracy.
The MCSCKF algorithm can effectively reduce the impact of heavy tail non Gaussian noise and improve the accuracy of vehicle state estimation.

1. Introduction

During the driving process of a vehicle, it relies on a stable control system. A stable and reliable control system depends on accurately obtaining the state parameters of the vehicle, which is a key factor. The accurate estimation has a significant impact on the active safety system of automobiles. Accurately obtaining vehicle operating parameters is the foundation and prerequisite for vehicles. The intelligentization of automobiles has great advantages in improving driving safety, reducing traffic accidents, enhancing traffic efficiency, and promoting energy conservation and emission reduction. It has become a hot issue in the development of the global automotive industry. The process of intelligent vehicle movement and driving can be divided into environmental perception, decision-making and motion control. Among them, environmental perception is the basic link of intelligent vehicle decision-making and motion control, mainly including the perception of the surrounding environment of the vehicle and the perception of the own state of the vehicle. Therefore, the accuracy of the own state perception of the vehicle directly affects the accuracy of the intelligent decision-making planning and the stability of motion control. Conducting the perception of vehicle operating state parameters is of great significance for improving the stability of intelligent vehicle control operation. However, due to the limitations of sensing measurement technology and cost, some key state variables of vehicles cannot be directly measured by existing sensors or the measurement cost is too high. To overcome this problem, low-cost sensors are used to easily obtain information. And vehicle models combined with state estimation calculation methods are used to estimate the driving state of vehicles, which has become an important means of obtaining driving state parameters [1-3].

The problem of vehicle state estimation has been widely studied. A brief review is presented in what follows.

Guo et al. combined the estimation algorithm of unscented Kalman filter with the estimation algorithm of lightweight convolutional neural network, and proposed a confidence based fusion strategy of vision and vehicle dynamics, which achieved the estimation of road adhesion coefficient [4]. Compared with EKF, the UKF can be applied to nonlinear distributed systems, achieving higher computational accuracy [5-10]. However, prior knowledge of system noise statistics significantly affects the performance of UKF. If the design of system noise statistical characteristics is not accurate, the filtering results of UKF will deteriorate or even diverge [11, 12]. Similar to UKF, the cubature Kalman filter (CKF) also requires accurate design of the statistical characteristics of system noise [13, 14]. Hu et al. presented a novel direct filtering approach to INS/GNSS (Inertial Navigation System / Global Navigation Satellite System) integration [15]. Cubature-Kalman filter is widely used for nonlinear dynamic estimations due to its high accuracy and numerical stability [16-20]. Adaptive Unscented Kalman Filter (AUKF) is an effective system error estimation method that can suppress the interference of inaccurate system noise statistics on the filtering results. However, the above AUKF method mainly weakened the impact of system errors by improving the statistical characteristics of system noise, without directly estimating and compensating for the system errors of the observation model, resulting in limited ability to suppress the impact of observation model system errors. Meng et al. presented an adaptive UKF with noise statistic estimator to overcome the limitation of the standard UKF [21]. Wan et al. introduced the Huber cost function to the UKF algorithm for correction of measurement noise. The experiment showed that the algorithm effectively suppressed the influence of abnormal noise [22]. Zhang et al. proposed CKF based on high-order cubature rules, but complex and lengthy high-order criteria could affect the real-time performance of the algorithm [23]. Liu et al. combined EKF with fuzzy algorithm to achieve adaptive adjustment of EKF estimation, which improved the accuracy and robustness of driving state estimation [24]. Zhou et al. integrated genetic algorithm and adaptive neural fuzzy inference system for vehicle state estimation [25]. Chen et al. proposed a hierarchical series state estimation of EKF based on the established 3-DOF vehicle dynamics model, and conducted joint simulation verification [26]. Liu et al. proposed a machine learning regression algorithm for particle swarm optimization neural networks, which used low-cost sensors to obtain easily measurable parameters for model training and estimated the required variables [27]. Gao et al. designed a HNN hybrid neural network architecture for vehicle motion state estimation, which was robust to changes in road adhesion coefficient and achieved deep learning estimation of vehicle motion state [28]. At present, there was still relatively little research on Support Vector Regression (SVR) in estimating the driving state of automobiles. However, the SVR algorithm had been applied in other fields such as predictive analysis and parameter estimation, and had achieved good estimation results [29, 30]. Hao et al. used a standard EKF method to estimate the yaw rate and side slip angle based on a 3-DOF vehicle model, and verified its effectiveness through simulation. However, its noise characteristics were obtained through experiments and experience, making it difficult to verify its accuracy and affecting the filtering effect [31]. Li et al. proposed an EKF vehicle state estimation method based on the fusion of multiple sensor information. Although it considered multiple sets of noise characteristics, it essentially assumed that the statistical characteristics of the noise were known, which limited its applicability [32]. Li et al. proposed an adaptive volumetric Kalman filter, which combines the standard cubic Kalman filter with the Sage Husa suboptimal estimation algorithm to estimate some vehicle parameters in real-time online. Although this method solved the problem of estimating noise covariance, the Sage Husa suboptimal estimation method could easily cause the noise covariance to lose its positive definiteness and lead to filter divergence [31]. Cubature-Kalman filter is widely used for nonlinear dynamic estimations due to its high accuracy and numerical stability.

The above research mainly focuses on algorithms such as KF, EKF, UKF and CKF. These algorithms exhibit good state estimation performance under Gaussian noise conditions. However, in practical applications, noise often presents a non Gaussian distribution, and system model nonlinearity can lead to increased estimation errors. Therefore, the paper proposes a MCSCKF method. And simulation experiment is conducted through Carsim and Matlab/Simulink to verify the accuracy and robustness of the algorithm. At the same time, the above literature had effectively identified vehicle parameters through various methods, but some methods used were difficult to achieve effective estimation for systems with many parameters and strong nonlinearity. And the vehicle state and parameters were considered less when estimating vehicle parameters. The vehicle quality directly affected the yaw moment of inertia, center of mass position and height, lateral load transfer, which in turn affected the tire lateral force, and ultimately affected variables that characterized the vehicles state, such as speed, acceleration, yaw rate, and center of mass lateral angle.

2. Mathematical model of vehicle dynamics

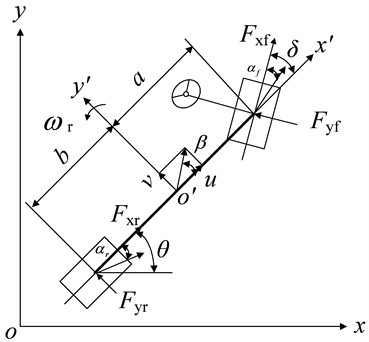
2.1. 3-DOF vehicle model

The vehicle state estimation model is established based on a 3-DOF vehicle model:

Fig. 13-DOF vehicle model

The dynamic equation of the 3-DOF vehicle model is as follows [34]:

1

{\dot{ω}}_{r} = \frac{a^{2} k_{1} + b^{2} k_{2}}{I_{z}} \frac{ω_{r}}{u} + \frac{a k_{1} - b k_{2}}{I_{z}} β - \frac{a k_{1}}{I_{z}} δ,

2

\dot{β} = \frac{a k_{1} - b k_{2} - m u^{2}}{m} \frac{ω_{r}}{u^{2}} + \frac{k_{1} + k_{2}}{m} \frac{β}{u} - \frac{k_{1} δ}{m u},

3

\dot{u} = a_{x} + v x,

4

a_{y} = \frac{a k_{1} - b k_{2}}{m u} ω_{r} + \frac{k_{1} + k_{2}}{m} β - \frac{k_{1}}{m} δ .

The side slip angle is:

5

β = \arctan \frac{ν}{u} .

2.2. Tire model

The lateral forces of front and rear wheels can be expressed as:

6

\{\begin{array}{l} F_{y f} = c_{f} α_{f}, \\ F_{y r} = c_{r} α_{r}, \end{array}

where $c_{f}$ and $c_{r}$ are the lateral stiffness values of the front and rear tires. $α_{f}$ and $α_{r}$ are the front and rear slip angles:

7

\{\begin{array}{l} c_{f} = \frac{\partial F_{y f}}{\partial α_{f}}| α_{f} = 0, \\ c_{r} = \frac{\partial F_{y r}}{\partial α_{r}}| α_{r} = 0 . \end{array}

3. The DCKF observation algorithm

3.1. Standard SCKF algorithm

The state and observation equations based on vehicle model are as following:

8

\{\begin{array}{l} \dot{x} (t) = f [x (t), u (t)] + w (t), \\ z (t) = h [x (t), u (t)] + v (t), \end{array}

where $x (t)$ , $u (t)$ and $z (t)$ are the state, control and observation variables respectively; $w (t)$ and $v (t)$ are the process and observation noise respectively. And $x (t) = [v_{x}, v_{y}, ω_{r}]^{T};$ $u (t) = [a_{x}, a_{y}, ω_{r}, F_{x i j}, F_{y i j}]^{T}$ ; $z (t) = [a_{x}, a_{y}, ω_{r}]^{T}$ .

The nonlinear discrete-time state and measurement equations are:

9

\{\begin{array}{l} x_{k} = f (x_{k - 1}, u_{k - 1}) + w_{k - 1}, \\ z_{k} = h (x_{k}, u_{k}) + v_{k}, \end{array}

where $x_{k}$ , $u_{k}$ and $z_{k}$ are the state, input and observation vector; $w_{k}$ is the process noise; $v_{k}$ is the measurement noise. And the uncorrelated covariance is:

10

\{\begin{array}{l} E (w_{k - 1}, w_{j - 1}^{T}) = Q_{k - 1}, \\ E (v_{k}, v_{j - 1}^{T}) = R_{k} δ_{k j}, \end{array}

where $Q_{k - 1}$ and $R_{k}$ are non negative definite and positive definite matrix respectively; $δ_{k j}$ is the Kronecker function, $Q$ and $R$ are the measurement noise matrix and the process noise matrix respectively.

The specific implementation process of the SCKF algorithm is as follows:

1) Initialization.

2) Time updating:

11

\{\begin{array}{l} x_{k - 1 |k - 1}^{i} = {\hat{x}}_{k - 1 |k - 1} + S_{k - 1 |k - 1} ζ_{i}, \\ x_{k - 1 |k - 1}^{i *} = f (x_{k - 1 |k - 1}^{i}), i = 1,2, \dots, 2 n, \end{array}

where $ζ_{i}$ is the $i$ th column of the volume point weight matrix $[\sqrt{n} I_{n}, - \sqrt{n} I_{n}]$ ; $I_{n}$ is an identity matrix of $n \times n$ ; $n$ is the dimension of the state variable.

When the volume point $x_{k |k - 1}^{i *}$ after propagation is determined, the state prediction value ${\hat{x}}_{k |k - 1}$ and the square root number $S_{k |k - 1}$ of the prediction error covariance matrix can be calculated accordingly:

12

{\hat{x}}_{k |k - 1} = \frac{1}{2 n} \sum_{i = 1}^{2 n} x_{k |k - 1}^{i *},

13

S_{k |k - 1} = T r i a ([X_{k |k - 1}^{i *}, c h o l (Q_{k - 1})]),

where $x_{k |k - 1}^{i *}$ represents the weighted center matrix; $S$ is the lower triangular matrix:

14

S = T r i a (A) = R^{T} .

3) Measurement updating.

Updating volume points:

15

x_{k |k - 1}^{i} = {\hat{x}}_{k |k - 1} + S_{k |k - 1} ζ_{i}, i = 1,2, \dots, 2 n .

The propagation volume point of the measurement equation is calculated:

16

z_{k |k - 1}^{i} = h (x_{k |k - 1}^{i}) .

The square root of the covariance matrix of the innovation error and the measurement prediction value are calculated:

17

{\hat{z}}_{k | k - 1} = \frac{1}{2 n} \sum_{i = 1}^{2 n} z_{k | k - 1}^{i},

18

S_{z z, k | k - 1} = T r i a ([\begin{array}{l} Z_{k | k - 1}, c h o l (R_{k}) \end{array}]),

where $Z_{k | k - 1}$ is the weighted central matrix.

Then the cross covariance matrix is calculated:

19

P_{x z, k | k - 1} = χ_{k | k - 1} Z_{k | k - 1}^{T},

where $χ_{k | k - 1}$ is the weighted central matrix.

Then the gain matrix is calculated:

20

K_{k | k - 1} = \frac{P_{x z, k | k - 1} / S_{x z, k | k - 1}^{T}}{S_{x z, k | k - 1}} .

The state variables and the error covariance matrix are updated:

21

{\hat{x}}_{_{k | k}} = {\hat{x}}_{_{k | k - 1}} + K_{_{k | k - 1}} (z_{_{k}} - {\hat{z}}_{_{k | k - 1}}),

22

S_{k | k} = T r i a ([x_{k | k} - K_{k} z_{k | k - 1}, K_{k} c h o l (R_{k})]) .

3.2. Maximum correlation entropy criterion

Firstly, the prior value of the noise covariance of SCKF needs to be determined. Due to the unknown prior statistics of noise and the uncertainty of the system model, the accuracy will significantly reduce under non Gaussian noise conditions. In order to solve the problem, SCKF is re-derived based on the MCC to improve its estimation accuracy and adaptability under non Gaussian noise conditions.

Correlation entropy is a kind of variable which measures the generalized similarity between two random variables [35]:

23

V (X, Y) = E [κ (X, Y)] = \int κ (X, Y) ρ_{X Y} (x, y),

where $E (\cdot)$ represents expectation; $κ (\cdot)$ represents the Mercer kernel function which can be replaced by the Gaussian kernel function:

24

κ (x, y) = G (e) = e x p (- \frac{e^{2}}{2 σ^{2}}),

where $e = x - y$ ; $σ$ is the core bandwidth.

Due to the difficulty in obtaining the joint distribution function $ρ_{X Y} (x, y)$ in most cases, the sample mean is used here to approximate the joint distribution function:

25

\hat{V} (X, Y) = \frac{1}{N} \sum_{i = 1}^{N} G_{σ} (e (i)),

where $e (i) = x (i) - y (i)$ . And the $x$ , $y$ satisfying ${\{x (i), y (i)\}}_{i = 1}^{N}$ . By expanding with Taylor series, the following equation can be obtained:

26

V (X, Y) = \sum_{n = 0}^{\infty} \frac{{(- 1)}^{n}}{2^{n} σ^{2 n} n!} E [{(X - Y)}^{2 n}] .

The kernel bandwidth $σ$ is expressed as higher-order moments of second order or higher.

3.3. Maximum correlation entropy SCKF

The specific process of re-deriving for SCKF based on maximum correlation entropy is as follows [36]:

27

[\begin{matrix} {\hat{x}}_{k ∣ k - 1} \\ z_{k} \end{matrix}] [\begin{matrix} x_{k} \\ h (x_{k}, u_{k}) \end{matrix}] + ϕ_{k},

where, the covariance matrix $ϕ_{k}$ can be obtained by Eq. (28):

28

ϕ_{k} = [\begin{matrix} {\hat{x}}_{k | k - 1} - x_{k} \\ r_{k} \end{matrix}],

29

B_{k} B_{k}^{T} = [\begin{matrix} S_{k | k - 1} S_{k | k - 1}^{T} & 0 \\ 0 & S_{R, k} S_{R, k}^{T} \end{matrix}] .

Eq. (30) can be obtained by multiplying both sides of Eq. (27) by $B_{k}^{- 1}$ :

30

D_{k} = g (x_{k}, u_{k}) + e_{k} .

The cost function can be rewritten as:

31

J_{M C C} (x_{k}) = \sum_{i = 1}^{n + m} G_{σ} (e_{i, k}) = \sum_{i = 1}^{n + m} G_{σ} (d_{i, k} - g_{i} (x_{k}, u_{k})),

where $d_{i, k}$ represents the $i$ th element of $D_{k}$ .

The optimal value of state estimation can be solved by maximizing the cost function as follows:

32

{\hat{x}}_{k} = a r g \underset{x_{k}}{m a x} \sum_{i = 1}^{n + m} G_{σ} (e_{i, k}) .

First-order derivative of Eq. (32) is implemented and is set to zero.

Eq. (33) can be obtained by setting $C_{i, k} = G_{σ} (e_{i, k})$ :

33

C_{k} = d i a g (G_{σ} (e_{1, k}), \dots, G_{σ} (e_{n + m, k})) = [\begin{matrix} C_{x, k} & 0 \\ 0 & C_{y, k} \end{matrix}] .

Eq. (34) can be obtained by reweighting the covariance matrix of the residuals using $C_{k}$ and reconstructing the measurement equation named ${\tilde{ψ}}_{k}$ :

34

{\tilde{ψ}}_{k} = [\begin{matrix} {\tilde{P}}_{k | k - 1} & 0 \\ 0 & {\tilde{R}}_{k} \end{matrix}] = B_{k} \cdot C_{k}^{- 1} \cdot B_{k}^{T} .

Eqs. (28-29) can be rewritten based on Eq. (34) as:

35

{\tilde{ψ}}_{x, k} = S_{k | k - 1} \cdot I \cdot S_{k | k - 1}^{T} = P_{k | k - 1},

36

{\tilde{R}}_{k} = S_{R, k} C_{y, k}^{- 1} S_{R, k}^{T} .

Then $R_{k}$ is replaced by substituting ${\tilde{R}}_{k}$ calculated by Eq. (36) into Eq. (18).

The measurement innovation $μ_{k}$ is defined as the error between the actual value of the measurement variable and its predicted value [37-39]:

37

μ_{k} = z_{k} - {\hat{z}}_{k |k - 1} .

The predicted value of the measurement variable can be calculated by Eq. (38):

38

{\hat{z}}_{k |k - 1} = \frac{1}{2 n} \sum_{i = 1}^{2 n} h (x_{k |k - 1}^{i}, u_{k}) .

The normalised measurement innovation is defined as:

39

{\bar{μ}}_{k} = (P_{k |k - 1}^{z z})^{- 1 / 2} μ_{k} .

A scale factor $η_{k}$ is introduced to comprehensively evaluate the relationship between the optimal kernel width and the standardised measurement innovation:

40

η_{k} = \sqrt{{\bar{μ}}_{k}^{T} {\bar{μ}}_{k}} = \sqrt{μ_{k}^{T} (P_{k |k - 1}^{z z})^{- 1} μ_{k}} .

Furthermore, the adaptive kernel width can be defined as:

41

σ_{k} = \frac{e x p (- η_{k}^{2})}{η_{k}} .

Combining Eq. (37) to Eq. (41), it can be seen that the adaptive kernel width $σ_{k}$ can be adaptively adjusted based on the measurement variables $z_{k}$ , the measurement prediction ${\hat{z}}_{k |k - 1}$ and the measurement covariance matrix $P_{k |k - 1}^{z z}$ .

4. Numerical simulation and experimental verification

4.1. Numerical simulation

The CarSim software is used to verify the performance of the proposed algorithm.

The CarSim simulation platform interface consists of three main parts: Vehicle parameters and simulation condition settings: This part mainly inputs vehicle and road data, simulation conditions, external environment and other parameters. Mathematical model solving: This part, also known as the main running program, is the core part of mathematical model solving operations. By setting simulation time, simulation step size, and other information, accurate and rapid analysis of automotive dynamics models can be carried out. Calculation results: The main function of this section is to view the animation and curves of the simulation results. The dynamic response characteristics of the vehicle will be presented in a curve form that is intuitive and vivid, making it convenient for users to perform post-processing on the calculation results. At present the CarSim software is mainly used for research on automotive safety and intelligent driving. And a small number of scholars have also applied it to road geometry design. CarSim software provides some original models of sedans, SUVs, light trucks, and multi-purpose transport vehicles. Users can first select the vehicle model, modify the vehicle parameters, and then set the test conditions for simulation analysis using a mathematical model solver. In the calculation results and post-processing interface, animation display and curve drawing can be used to analyze the performance of the vehicle simulation model.

Carsim is a globally leading software for simulating automotive dynamic behavior, which can accurately simulate and analyze the motion state of vehicles in various driving situations in a virtual environment. CarSim software, as the mainstream software for automotive kinematic simulation, comes with various test models and has good scalability. It can be connected with external software such as Simulink to conduct relevant testing and analysis of automotive handing performance through joint modeling, algorithm selection, and input of real vehicle parameters. The accurate setting of parameters is of great significance for simulation operations.

The initial speed of the vehicle is set as 80 km/h, and road adhesion coefficient is set as 0.8. The measurement noise matrix $Q$ and the process noise matrix $R$ are set as $Q = d i a g [\begin{array}{l} 0.105 & 0.105 & 0.105 \end{array}]$ , $R = 0.1 \cdot d i a g [\begin{array}{l} 0.205 & 0.205 & 0.205 \end{array}]$ . The double lane changing road is set as the simulation condition. The input signal is shown in Fig. 2.

Fig. 2Input signal of the steering angle

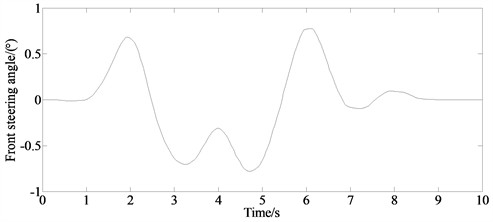
Fig. 3 is the simulation result of yaw rate. From the figure, it can be seen that the estimation results obtained by both the EKF and the MCSCKF algorithms are relatively satisfactory. However, when the road curvature changes, the estimation error of the EKF algorithm fluctuates indicating an increasing trend. The fitting degree between the data values output by MCSCKF and Carsim is relatively high, and the overall fluctuation of MCSCKF algorithm is smaller compared to the EKF algorithm. This is because the SCKF algorithm based on the maximum entropy correlation criterion uses the maximum entropy principle to select the most uncertain state distribution, which can better adapt to non Gaussian noise and measurement errors. At the same time, the orthogonal triangular decomposition method ensures the positive definiteness of the covariance matrix, which can suppress the impact of non Gaussian noise on estimation performance effectively.

Fig. 4 is the simulation result of the side slip angle. From the figure it can be seen that the estimated values of the side slip angle obtained by the EKF and MCSCKF algorithm are extremely close to the value obtained by Carsim. And the mean of absolute error of side slip angle obtained by the MCSCKF algorithm is lower than that of the EKF algorithm. This is because the MCSCKF algorithm can effectively reduce the impact of non Gaussian noise, thereby reducing system errors caused by noise and improving the accuracy and robustness.

Fig. 3Simulation result of yaw rate

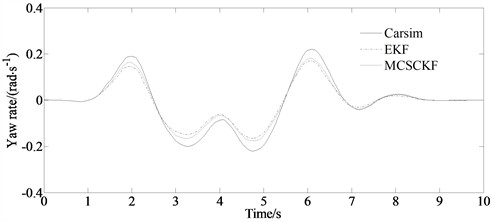
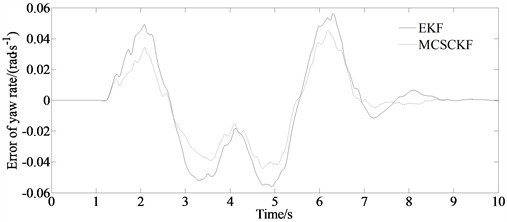
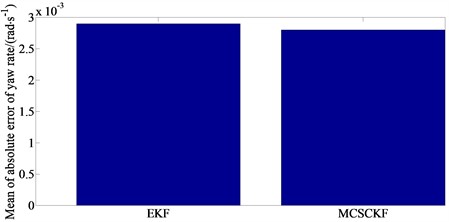
Fig. 4Simulation result of side slip angle

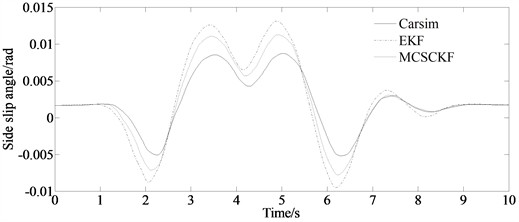
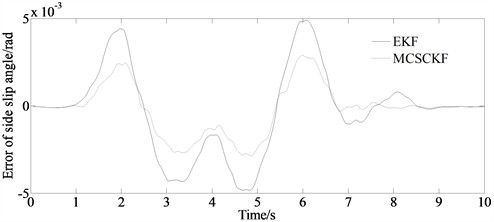
Fig. 5 is the simulation result of longitudinal velocity. It can be seen that the EKF algorithm has significant errors in estimating longitudinal velocity. On the one hand, this is due to the continuous turning of the vehicle at high speed and the continuous variation of road adhesion coefficients, which leads to system uncertainty. On the other hand, it is affected by non Gaussian noise, resulting in significant errors in the estimated data. However, the MCSCKF algorithm can better fit the reference data, indicating better adaptability and stronger robustness. At the same time, the MCSCKF algorithm can more stably and accurately estimate various parameters of the vehicle during driving process, with higher accuracy and anti-interference ability.

Fig. 5Simulation result of longitudinal velocity

4.2. Effectiveness verification

The input of front steering angle under the double lane changing condition is shown in Fig. 6.

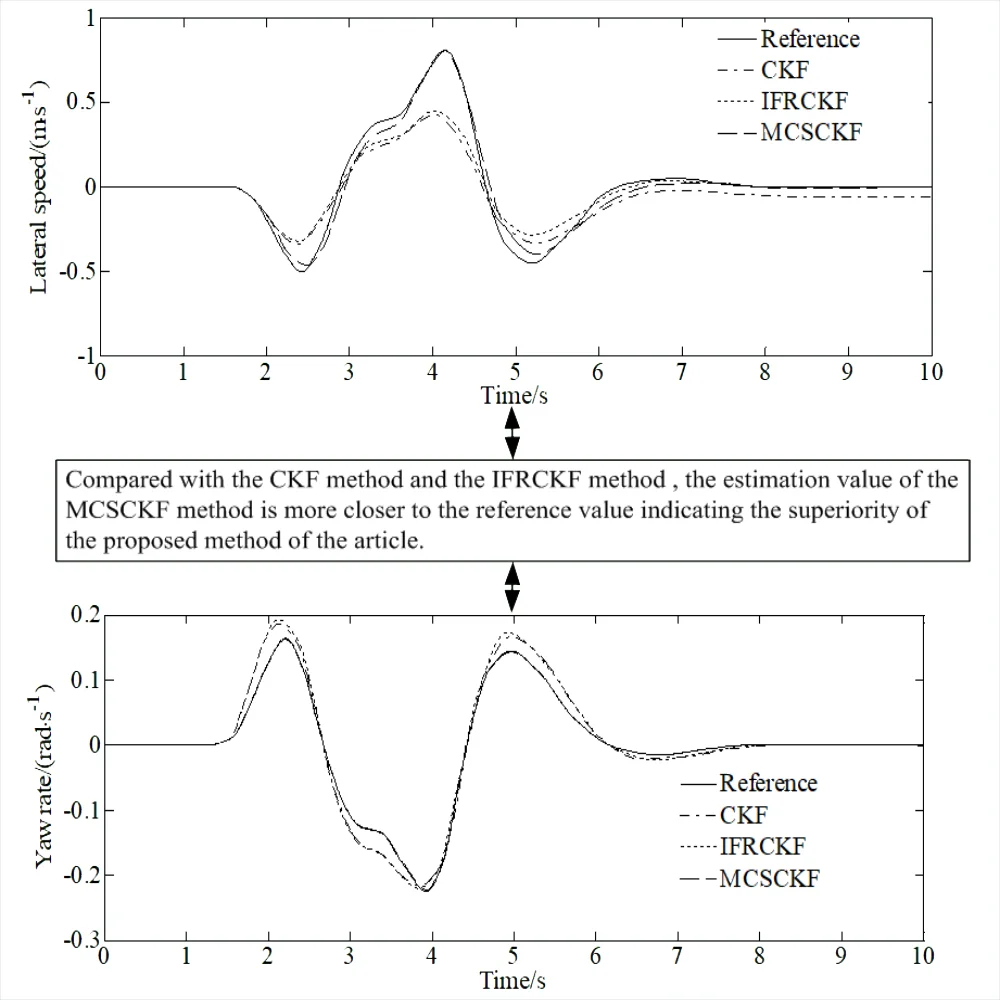
The comparison results of different methods are shown in Fig. 7.

From the comparison results of different methods, it can be seen that compared with the CKF method and the IFRCKF method proposed in Reference [15], the estimation value of the MCSCKF method is more closer to the reference value indicating the superiority of the proposed method of the article.

Fig. 6Input of front steering angle

Fig. 7Comparison results of different methods

a) Lateral speed

b) Yaw rate

4.3. Experimental verification

A real vehicle test is conducted to verify the effectiveness of the algorithm. The real experiment vehicle is shown in Fig. 8.

Fig. 8Real test vehicle

During the experiment, the gyroscope which is shown in Fig. 9(a) is used to collect signals to obtain yaw rate signals of the vehicle. The steering torque/angle tester which is shown in Fig. 9(b) is used to collect the steering angle signal.

Fig. 9Measurement equipments

a)

b)

Fig. 10Comparison of the estimated and test values

a) Input signal of the steering angle

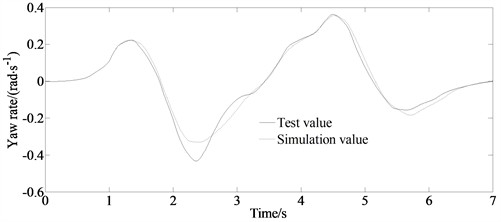
b) Yaw rate

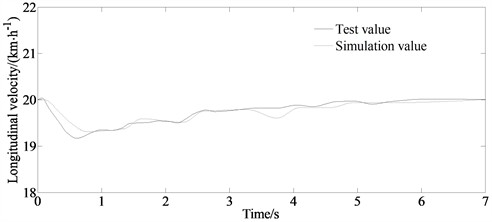
c) Longitudinal velocity

Fig. 10 is the comparison results of the yaw rate and the longitudinal. From Fig. 10 it can be seen that the longitudinal velocity change rate estimated by MCSCKF is relatively low. And also, there are errors between the test value and the simulation value both for the yaw rate and the longitudinal velocity. However, the change trends of the yaw rate and the longitudinal velocity are consistent with the test values. Based on the real vehicle verification, it can be seen that the MCSCKF algorithm achieves good accuracy in estimating vehicle state parameters under real vehicle conditions, further verifying the effectiveness of the proposed estimation algorithm.

5. Conclusions

This article proposes the MCSCKF algorithm to address the problem of decreased filtering accuracy of traditional Kalman filters under non Gaussian noise conditions. Based on a nonlinear 3-DOF vehicle dynamics model this article improves the SCKF using the maximum correlation entropy criterion to estimate the states of the yaw rate and the side slip angle as well as the longitudinal velocity of the vehicle. The effectiveness of the proposed algorithm is verified under double lane changing condition and compared with the EKF algorithm. The simulation results show that compared with the traditional EKF algorithm, the algorithm has a significant improvement in filtering accuracy. And the algorithm has higher accuracy and shorter running time. Real vehicle experiment is implemented to verify the effectiveness of the algorithm proposed in this paper, which has certain reference significance for engineering practice. The estimation algorithm based on the maximum correlation entropy criterion proposed in this article has high accuracy and provides ideas for improving vehicle state estimation, with good engineering application value. The MCSCKF algorithm can better fit the reference data, indicating better adaptability and stronger robustness. At the same time, the MCSCKF algorithm can more stably and accurately estimate various parameters of the vehicle during driving process, with higher accuracy and anti-interference ability.

References

Y. Liu, D. Cui, and W. Peng, “Optimum control for path tracking problem of vehicle handling inverse dynamics,” Sensors, Vol. 23, No. 15, p. 6673, Jul. 2023, https://doi.org/10.3390/s23156673

Publisher
Y. Liu, D. Cui, and W. Peng, “Optimal lane changing problem of vehicle handling inverse dynamics based on mesh refinement method,” IEEE Access, Vol. 11, pp. 115617–115626, Jan. 2023, https://doi.org/10.1109/access.2023.3324422

Publisher
Y. Liu and D. Cui, “Vehicle dynamics prediction via adaptive robust unscented particle filter,” Advances in Mechanical Engineering, Vol. 15, No. 5, p. 168781322311707, May 2023, https://doi.org/10.1177/16878132231170766

Publisher
H. Guo, X. Zhao, J. Liu, Q. Dai, H. Liu, and H. Chen, “A fusion estimation of the peak tire-road friction coefficient based on road images and dynamic information,” Mechanical Systems and Signal Processing, Vol. 189, p. 110029, Apr. 2023, https://doi.org/10.1016/j.ymssp.2022.110029

Publisher
Y. Chen, H. Yan, and Y. Li, “Vehicle state estimation based on Sage-Husa adaptive unscented Kalman filtering,” World Electric Vehicle Journal, Vol. 14, No. 7, p. 167, Jun. 2023, https://doi.org/10.3390/wevj14070167

Publisher
X. Dong, G. Hu, B. Gao, Y. Zhong, and W. Ruan, “Windowing-Based factor graph optimization with anomaly detection using Mahalanobis distance for underwater INS/DVL/USBL integration,” IEEE Transactions on Instrumentation and Measurement, Vol. 73, pp. 1–13, Jan. 2024, https://doi.org/10.1109/tim.2024.3353286

Publisher
G. Hu, L. Xu, B. Gao, L. Chang, and Y. Zhong, “Robust unscented Kalman filter-based decentralized multisensor information fusion for INS/GNSS/CNS integration in hypersonic vehicle navigation,” IEEE Transactions on Instrumentation and Measurement, Vol. 72, pp. 1–11, Jan. 2023, https://doi.org/10.1109/tim.2023.3281565

Publisher
G.-G. Hu, S.-S. Gao, Y.-M. Zhong, and B.-B. Gao, “Stochastic stability of the derivative unscented Kalman filter,” Chinese Physics B, Vol. 24, No. 7, p. 070202, Jul. 2015, https://doi.org/10.1088/1674-1056/24/7/070202

Publisher
G. Hu, B. Gao, Y. Zhong, L. Ni, and C. Gu, “Robust unscented Kalman filtering with measurement error detection for tightly coupled INS/GNSS integration in hypersonic vehicle navigation,” IEEE Access, Vol. 7, pp. 151409–151421, Jan. 2019, https://doi.org/10.1109/access.2019.2948317

Publisher
G. Hu, S. Gao, Y. Zhong, B. Gao, and A. Subic, “Modified strong tracking unscented Kalman filter for nonlinear state estimation with process model uncertainty,” International Journal of Adaptive Control and Signal Processing, Vol. 29, No. 12, pp. 1561–1577, May 2015, https://doi.org/10.1002/acs.2572

Publisher
Y. Wang, Y. Li, and Z. Zhao, “State parameter estimation of intelligent vehicles based on an adaptive unscented Kalman filter,” Electronics, Vol. 12, No. 6, p. 1500, Mar. 2023, https://doi.org/10.3390/electronics12061500

Publisher
S. Chu, H. Qian, and P. Ding, “Improved maximum correntropy unscented Kalman filter for spacecraft attitude estimation,” International Journal of Control, Automation and Systems, Vol. 21, No. 6, pp. 2020–2030, May 2023, https://doi.org/10.1007/s12555-022-0038-3

Publisher
H. Zong, Z. Gao, W. Wei, Y. Zhong, and C. Gu, “Randomly weighted CKF for multisensor integrated systems,” Journal of Sensors, Vol. 2019, pp. 1–19, Nov. 2019, https://doi.org/10.1155/2019/1216838

Publisher
B. Gao, G. Hu, X. Zhu, and Y. Zhong, “A robust cubature Kalman filter with abnormal observations identification using the Mahalanobis distance criterion for vehicular INS/GNSS integration,” Sensors, Vol. 19, No. 23, p. 5149, Nov. 2019, https://doi.org/10.3390/s19235149

Publisher
G. Hu, W. Wang, Y. Zhong, B. Gao, and C. Gu, “A new direct filtering approach to INS/GNSS integration,” Aerospace Science and Technology, Vol. 77, pp. 755–764, Jun. 2018, https://doi.org/10.1016/j.ast.2018.03.040

Publisher
G. Hu, L. Xu, Z. Yang, B. Gao, and Y. Zhong, “Indirect fuzzy robust cubature-Kalman filter with normalized input parameters,” IEEE Transactions on Aerospace and Electronic Systems, Vol. 60, No. 5, pp. 5880–5890, Oct. 2024, https://doi.org/10.1109/taes.2024.3397245

Publisher
B. Gao, G. Hu, Y. Zhong, and X. Zhu, “Cubature Kalman filter with both adaptability and robustness for tightly-coupled GNSS/INS integration,” IEEE Sensors Journal, Vol. 21, No. 13, pp. 14997–15011, Jul. 2021, https://doi.org/10.1109/jsen.2021.3073963

Publisher
B. Gao, W. Li, G. Hu, Y. Zhong, and X. Zhu, “Mahalanobis distance-based fading cubature Kalman filter with augmented mechanism for hypersonic vehicle INS/CNS autonomous integration,” Chinese Journal of Aeronautics, Vol. 35, No. 5, pp. 114–128, May 2022, https://doi.org/10.1016/j.cja.2021.08.035

Publisher
B. Gao, G. Hu, L. Zhang, Y. Zhong, and X. Zhu, “Cubature Kalman filter with closed-loop covariance feedback control for integrated INS/GNSS navigation,” Chinese Journal of Aeronautics, Vol. 36, No. 5, pp. 363–376, May 2023, https://doi.org/10.1016/j.cja.2022.12.008

Publisher
B. Gao, G. Hu, Y. Zhong, and X. Zhu, “Cubature rule-based distributed optimal fusion with identification and prediction of kinematic model error for integrated UAV navigation,” Aerospace Science and Technology, Vol. 109, p. 106447, Feb. 2021, https://doi.org/10.1016/j.ast.2020.106447

Publisher
Y. Meng, S. Gao, Y. Zhong, G. Hu, and A. Subic, “Covariance matching based adaptive unscented Kalman filter for direct filtering in INS/GNSS integration,” Acta Astronautica, Vol. 120, pp. 171–181, Mar. 2016, https://doi.org/10.1016/j.actaastro.2015.12.014

Publisher
W. Wan, J. Feng, B. Song, and X. Li, “Huber-based robust unscented Kalman filter distributed drive electric vehicle state observation,” Energies, Vol. 14, No. 3, p. 750, Feb. 2021, https://doi.org/10.3390/en14030750

Publisher
X. Zhang, Z. Yan, and Y. Chen, “High‐degree cubature Kalman filter for nonlinear state estimation with missing measurements,” Asian Journal of Control, Vol. 24, No. 3, pp. 1261–1272, Jan. 2021, https://doi.org/10.1002/asjc.2510

Publisher
M. C. Liu, Z. B. Peng, and X. J. Wu, “Joint estimation of vehicle motion state based on adaptive fuzzy extended Kalman filter,” Automobile Technology, Vol. 559, No. 4, pp. 23–30, 2022, https://doi.org/10.19620/j.cnki.1000-3703.20210263

Publisher
W. Q. Zhou, X. Qi, L. Chen, and X. Xu, “Vehicle state estimation based on the combination of unscented Kalman filtering and genetic algorithm,” Automotive Engineering, Vol. 41, No. 2, pp. 198–205, 2019, https://doi.org/10.19562/j.chinasae.qcgc.2019.02.012

Publisher
L. Chen, Q. B. Liu, and L. Tao, “Vehicle state parameter estimation based on graded series extended Kalman filter method,” Journal of Northeastern University Natural Science, Vol. 44, No. 8, pp. 1144–1151, 2023, https://doi.org/10.12068/j.issn.1005-3026.2023.08.011

Publisher
Y. Liu, Q. Sun, and D. Cui, “Vehicle state estimation based on PSO-RBF neural network,” International Journal of Vehicle Safety, Vol. 11, No. 1, p. 93, Jan. 2019, https://doi.org/10.1504/ijvs.2019.101307

Publisher
Z. H. Gao, W. H. Wen, M. H. Tang, J. Zhang, and G. Y. Chen, “Estimation of vehicle motion state based on hybrid neural network,” Automotive Engineering, Vol. 44, No. 10, pp. 1527–1536, 2022, https://doi.org/10.19562/j.chinasae.qcgc.2022.10.007

Publisher
Y. Liang, Y. J. Zhou, S. X. Jiang, X. Yuan, and S. Zhang, “Lithium battery SoH estimation based on improved GwO-SVR,” Electronic Measurement Technology, Vol. 46, No. 7, pp. 13–18, 2023, https://doi.org/10.19651/j.cnki.emt.2211051

Publisher
Y. He, Z. Xiao, Y. F. Li, P. C. Wu, D. G. Liu, and J. Du, “An assembly quality prediction method for automotive instrument clusters using CNN-SVR,” China Mechanical Engineering, Vol. 33, No. 7, pp. 825–833, 2022, https://doi.org/10.3969/j.issn.1004-132x.2022.07.009

Publisher
L. Hao, G. Li, S. W. Liu, L. Wang, and W. Sun, “Application of EKF soft computing in vehicle state estimation,” Chinese Journal of Construction Machinery, Vol. 15, No. 5, pp. 466–450, 2017, https://doi.org/10.15916/j.issn1674-3261.2017.06.008

Publisher
J. Li and J. Zhang, “Vehicle sideslip angle estimation based on hybrid Kalman filter,” Mathematical Problems in Engineering, Vol. 2016, No. 5, pp. 1–10, Jan. 2016, https://doi.org/10.1155/2016/3269142

Publisher
J. Li, Q. J. Shi, L. Hong, and P. Liu, “Commercial vehicle ESC neural network sliding mode control based on vehicle state estimation,” Journal of Jilin University, (Engineering and Technology Edition), Vol. 50, No. 5, pp. 1545–1555, 2020, https://doi.org/10.13229/j.cnki.jdxbgxb20190535

Publisher
Y. Liu, D. Cui, and W. Peng, “Vehicle state and parameter estimation based on improved extend Kalman filter,” Journal of Measurements in Engineering, Vol. 11, No. 4, pp. 496–508, Dec. 2023, https://doi.org/10.21595/jme.2023.23475

Publisher
Z. D. Zhang, L. Zheng, Y. N., Li, H. Wu, and Y. H. Yu, “Research on intelligent vehicle target state tracking based on robust adaptive SCKF,” Journal of Mechanical Engineering, Vol. 57, No. 20, p. 181, Jan. 2021, https://doi.org/10.3901/jme.2021.20.181

Publisher
W. Gao, T. Yang, Z. W. Deng, and B. H. Wang, “Distributed state estimation for electric vehicles based on MCSKF,” Journal of Chongqing University of Technology, Vol. 37, No. 12, pp. 58–66, 2023, https://doi.org/10.3969/j.issn.1674-8425(z).2023.12.007

Publisher
Z. Zhang, L. Zheng, H. Wu, Z. Zhang, Y. Li, and Y. Liang, “An estimation scheme of road friction coefficient based on novel tyre model and improved SCKF,” Vehicle System Dynamics, Vol. 60, No. 8, pp. 2775–2804, Aug. 2022, https://doi.org/10.1080/00423114.2021.1928247

Publisher
W. Wei, S. Gao, Y. Zhong, C. Gu, and G. Hu, “Adaptive square-root unscented particle filtering algorithm for dynamic navigation,” Sensors, Vol. 18, No. 7, p. 2337, Jul. 2018, https://doi.org/10.3390/s18072337

Publisher
G. Gao, Y. Zhong, Z. Gao, H. Zong, and S. Gao, “Maximum correntropy based spectral redshift estimation for spectral redshift navigation,” IEEE Transactions on Instrumentation and Measurement, Vol. 72, pp. 1–10, Jan. 2023, https://doi.org/10.1109/tim.2023.3275992

Publisher

About this article

Received

19 July 2024

Accepted

04 November 2024

Published

02 January 2025

DOI

https://doi.org/10.21595/jme.2024.24376

Keywords

vehicle state estimation

square-root cubature Kalman Filter

maximum correntropy

Acknowledgements

This research was supported by the Open Research Program of Huzhou Key Laboratory of Urban Multidimensional Perception and Intelligent Computing under Grant No. UMPIC202404.

Data Availability

The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

Author Contributions

Yingjie Liu: mathematical model and the simulation techniques. Dawei Cui: spelling and grammar checking as well as virtual validation and virtual validation.

Conflict of interest

The authors declare that they have no conflict of interest.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Research article

2023 11 18

Vehicle state and parameter estimation based on adaptive anti-outlier unscented Kalman filter and GA-BPNN method

Yingjie Liu, Dawei Cui, Wen Peng

Research article

2023 10 30

Vehicle state and parameter estimation based on improved extend Kalman filter

Yingjie Liu, Dawei Cui, Wen Peng

Research article

2023 08 01

Minimum-time lane changing problem of vehicle handling inverse dynamics based on adaptive mesh refinement and collocation optimization method

Yingjie Liu, Dawei Cui, Wen Peng

Research article

2022 12 23

Moving horizon estimation of vehicle state and parameters

Yingjie Liu, Dawei Cui, Wen Peng

Y. Liu and D. Cui, “Estimation of vehicle state based on maximum correntropy square-root cubature Kalman Filter,” Journal of Measurements in Engineering, Vol. 13, No. 1, –15, Jan. 2025, https://doi.org/10.21595/jme.2024.24376

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jme.2024.24376
UR  - https://doi.org/10.21595/jme.2024.24376
TI  - Estimation of vehicle state based on maximum correntropy square-root cubature Kalman Filter
T2  - Journal of Measurements in Engineering
AU  - Liu, Yingjie
AU  - Cui, Dawei
PY  - 2025
DA  - 2025/01/02
PB  - Extrica
VL  - 13
IS  - 1
SN  - 2335-2124
SN  - 2424-4635
ER  - 

Copy Ris

Copied to clipboard!

 @article{Liu_2025, title={Estimation of vehicle state based on maximum correntropy square-root cubature Kalman Filter}, ISSN={2424-4635}, url={https://doi.org/10.21595/jme.2024.24376}, DOI={10.21595/jme.2024.24376}, journal={Journal of Measurements in Engineering}, publisher={JVE International Ltd.}, author={Liu, Yingjie and Cui, Dawei}, year={2025}, month=jan }

Copy Bibtex

Copied to clipboard!

[1]Y. Liu and D. Cui, “Estimation of vehicle state based on maximum correntropy square-root cubature Kalman Filter,” Journal of Measurements in Engineering, Jan. 2025, doi: 10.21595/jme.2024.24376.

Copy IEEE

Copied to clipboard!

Liu, Yingjie, and Dawei Cui. “Estimation of Vehicle State Based on Maximum Correntropy Square-Root Cubature Kalman Filter.” Journal of Measurements in Engineering, January 2, 2025. https://doi.org/10.21595/jme.2024.24376.

Copy Chicago

Copied to clipboard!

Estimation of vehicle state based on maximum correntropy square-root cubature Kalman Filter

Abstract

Highlights

1. Introduction

2. Mathematical model of vehicle dynamics

2.1. 3-DOF vehicle model

2.2. Tire model

3. The DCKF observation algorithm

3.1. Standard SCKF algorithm

3.2. Maximum correlation entropy criterion

3.3. Maximum correlation entropy SCKF

4. Numerical simulation and experimental verification

4.1. Numerical simulation

4.2. Effectiveness verification

4.3. Experimental verification

5. Conclusions

References

About this article

Related Articles