Critical buckling load analysis of Euler-Bernoulli beam on two-parameter foundations using Galerkin method

Ike, Charles Chinwuba

doi:10.21595/jmai.2024.24285

Journal of Mechatronics and Artificial Intelligence in Engineering

Browse Journal

Submit article

Published: 15 October 2024

Check for updates

Critical buckling load analysis of Euler-Bernoulli beam on two-parameter foundations using Galerkin method

Charles Chinwuba Ike¹

¹Department of Civil Engineering, Enugu State University of Science and Technology, Agbani, 402004, Enugu State, Nigeria

Cite the article Download PDF

Article in Press

Downloads 35

Abstract

The critical buckling load determination of Euler-Bernoulli beams on two-parameter elastic foundations (EBBo2PFs) is important to avert buckling failures. The governing equation for buckling of thin beam on two-parameter elastic foundation is a homogeneous ordinary differential equation (HODE) of fourth order and constant parameters when the beam is prismatic and homogeneous. The HODE has been solved in this work by Galerkin method for simply supported, clamped and clamped-simply supported ends. One-parameter algebraic shape function formulation was used to reduce the problem to an algebraic eigenvalue problem, which is solved to find the critical buckling load for each studied case. The critical buckling load for EBBo2PF for simply supported boundary conditions was found to be closely identical to the exact solutions. The solutions for clamped-clamped edges and clamped-simple supports were found to be accurate. The merit of the Galerkin method is the simplicity and the accuracy even when one-parameter shape function has been used.

Highlights

The Galerkin Variational method simplified the problem to an algebraic eigenvalue problem.
One-parameter shape function formulation of the Galerkin solution for simply supported EBBo2PFs gave critical buckling load solutions that are almost identical to exact solutions.
One-parameter Galerkin solutions for clamped clamped EBBo2PF gave critical buckling loads that differ from the previous results by 3.93% to 6.92%.
The present one-parameter Galerkin solution for EBBo2PF with CS supports gave differences varying from 4% to 5.26%.

1. Introduction

The differential equations of elastic stability of beams resting on elastic foundations have been derived by incorporating the reactive forces of the elastic foundation in the equation of beam stability. Beam models commonly used depend on the depth to thickness ratios. When the beam depth to thickness ratio is less than 0.05, the beam is called thin or slender beam. Euler-Bernoulli beam theory (EBBT) is used for thin beam because the Euler-Bernoulli-Navier orthogonality hypothesis used in the formulation disregards shear strain that play significant roles in the behaviour of moderately thick and thick beams. Timoshenko beam theory (TBT), shear deformable beam theories, and refined beam theories formulated by several researchers such as Dahake and Ghugal [1], Levinson [2], Sayyad and Ghugal [3], Ghugal and Shimpi [4], Yue [5], are used for moderately thick and thick beams where the depth to span ratios exceed 0.05.

This work assumes a depth to span ratio of beams to be less than 0.05, and hence uses EBBT.

Elastic foundation models have been derived based on discrete parameter and continuously distributed parameter assumptions. Discrete parameter models use discretization of the foundations at discrete points, and hence a limited number of parameters to describe the foundation. However, continuously distributed parameter models derive the foundation reactions using the mathematical theory of elasticity resulting in complex differential equations that are difficult to solve in analytical form. The inherent simplicity of the resulting mathematical representation of discrete parameter foundations make them more frequently used. Discrete parameter foundation models include (i) Winkler foundation model (ii) Pasternak, Vlasov, Hetenyi and Filonenko-Borodich foundations, and (iii) Kerr foundation.

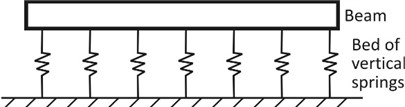
Winkler foundation model which is shown in Figure 1 is a one-parameter foundation model. The foundation is represented as a system of vertical, closely spaced, non-interacting linear elastic springs whose vertical stiffness is directly proportional to the vertical deflection of the point considered [6-8]. In the Winkler foundation, the foundation reaction $r (x)$ (at any point) is directly proportional to the beam deflection ( $w (x)$ ) at the point and the constant of proportionality is the Winkler foundation constant, $k$ , which is the one-parameter used to characterise the soil.

The equation for the foundation reaction ( $r (x)$ ) for the Winkler model is given [6-8]:

r (x) = k w (x) .

The main disadvantage of the Winkler foundation model is its failure to consider the shear interaction of the vertical springs and the resulting discontinuity of displacements caused.

Fig. 1Thin beam resting on a bed of vertical linear elastic springs

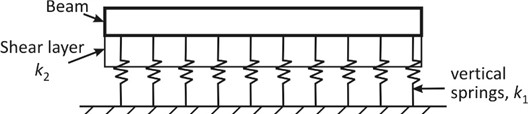
Two-parameter discrete foundation models were derived by Pasternak, Vlasov, Hetenyi and Filonenko-Borodich in order to overcome the displacement discontinuity issues in the one-parameter Winkler foundation model. In the two-parameter discrete foundation models, the foundation is represented using a bed of vertical, closely spaced, interacting linear elastic springs. Shear interactions are introduced between the adjoining vertical springs by the use of shear layer and coupling. The foundation is thus modelled using two-parameters; the first parameter, denoted by $k_{1}$ is the stiffness in the vertical direction, and is similar to the Winkler foundation parameter. The second parameter, $k_{2}$ , is the shear interaction effect of the vertical springs [9-11]. An illustration of two-parameter discrete foundation models is shown in Fig. 2, which presents it as a bed of closely spaced, vertical, interacting springs with adjoining springs linked together using shear coupling.

The foundation reaction $r (x)$ for two-parameter models is expressed by [9], [11]:

r (x) = k_{1} w (x) - k_{2} \frac{d^{2} w (x)}{d x^{2}} .

Kerr [12-14] presented a three-parameter discrete foundation model, which is rarely used.

Vlasov and Leontiev [15] used an energy minimization technique to derive the two-parameter Vlasov-Leontiev simplified elastic continuum foundation model. The model introduced an arbitrary parameter $γ_{1}$ to define the vertical distribution of soil deformation.

Jones and Xenophontoss [16] derived an expression for the vertical distribution parameter $γ_{1}$ in terms of the displacement characteristics, but failed to derive a method for finding $γ_{1}$ . In further studies, Vallabhan and Das [17, 18], found the $γ_{1}$ using an iterative procedure.

Fig. 2Beam supported on two-parameter discrete foundation graphically illustrated as a bed of vertical closely spaced, interacting linear elastic (Hookean) springs

Beam supported on two-parameter discrete foundation graphically illustrated as a bed of vertical closely spaced, interacting linear elastic (Hookean) springs

2. Literature review

Theory of elasticity methods were used for beam on elastic foundation and analysis by Akhazhanov et al. [19-22], Huang et al. [23], Akhmedeev et al. [24], Zhang et al. [25], and Gbolami and Alizadeh [26].

Gulkan and Alemdar [27] and Teodoru and Muscat [28] used the finite element method (FEM) to study beams on two-parameter elastic foundations. FEMs were also used for EBBoEF by Alzubaidi et al. [29], Wieckowski and Swiatkiewiez [30], and Worku and Habte [31].

Olotu et al. [32] used the differential transform method (DTM) to find numerical solutions for natural frequencies of non prismatic beams supported on variable one-parameter foundations. The DTM reduced the governing equation to an algebraic problem which was solved using computer algorithms for various boundary conditions. They however failed to solve buckling analysis of thin beams on elastic foundations using DTM.

Aslami and Akinov [33] presented closed form solutions of EBBo2PFs by reducing the governing equations to a system of first order differential equations, which were subsequently solved using Jordan method.

Hetenyi [34], Timoshenko and Gere [35], Wang et al. [36] have derived differential equations of buckling (DEoB) of Euler-Bernoulli beams on elastic foundations (EBBoEFs). They also derived analytical solutions to the DEoB for various boundary conditions.

Taha and Hadima [37] and Taha [38] used Recursive differentiation method (RDM) on the DEoB to obtain analytical solutions for the critical buckling loads of non uniform EBBoEFs. Soltani [39] presented a finite element method to solve the DEoB for EBBoEF. Aristizabal-Ochoa [40] and Hassan [41] have derived solutions for EBBoEFs under various boundary conditions. Anghel and Mares [42] used the method of collocation to solve the stability problems of EBBoEFs. Atay and Coskun [43] applied the Variational iteration method (VIM) to the analysis of the stability of EBBoEF for prismatic and non-prismatic cross-sectional beam geometries; and for variety of boundary conditions. Akgoz et al. [44] investigated the bending analysis of beams on elastic foundations but failed to study buckling analysis.

Ike [6] used the finite sine transform method (FSTM) to simplify the governing equation of free vibration of simply supported EBBoWF to an integral equation, and ultimately to an algebraic problem. The method was found suited for EBBoWF with Dirichlet boundary conditions because the sinusoidal function which is the integral kernel of the FSTM satisfies the geometric and force boundary conditions. The FSTM gave exact eigenvalues, but the work was not extended to buckling analysis.

Ike [7] utilized a point collocation method (PCM) to obtain approximate solution to the differential equation of flexure (DEoF) of Euler-Bernoulli beam resting on Winkler foundation (EBBoWF). In the PCM, the solutions were obtained in an approximate way only at the collocation points. Acceptable bending solutions that were comparable to previous solutions found in literature sources were obtained. However, the study failed to consider buckling analysis.

Ike [8] used the generalized integral transform method (GITM) to solve the free vibration problems of EBBoWF under various boundary conditions. In the GITM, the eigenfrequencies of free vibrations of thin beams with equivalent boundary conditions were used as kernel functions to formulate the boundary value problem (BVP) as an integral equation. The kernel functions used were exact shape functions, and the resulting eigenvalues were exact. However, the work did not consider bucking analysis.

Ike [9] used SVIM and sinusoidal shape functions to derive exact buckling loads of EBBo2PFs. Ike et al. [10] and Ike [11] utilized SVIM for buckling solutions of EBBo2PFs using polynomial shape function for beams with both ends clamped and beams with simply supported ends, respectively.

Ike et al. [45] used Picard’s successive iteration method to solve Euler buckling problem with pinned ends. Ofondu et al. [46] applied Stodola-Vianello iteration method (SVIM) to find solutions to Euler column buckling problems with one end clamped and the other on pin support. Ikwueze et al. [47] utilized Least squares weighted residual method (LSWRM) for the critical buckling load analysis of Euler columns with one end fixed and the other end pinned. Mama et al. [48] used fifth degree polynomials as shape functions in a FEM to obtain accurate critical buckling load solutions of EBBoWF.

Ike et al. [49] used the SVIM and polynomial functions that satisfy the boundary conditions of EBBoWF with both ends clamped to find satisfactory solutions for critical buckling loads. In another study, Ike [50] used the SVIM and polynomial functions that satisfy the simply supported boundary conditions to find approximate critical buckling load solutions for simply supported EBBoWF.

Ike [51] used SVIM and exact sinusoidal shape functions to obtain exact buckling solutions to simply supported EBBoWF.

Ike [52] used Fourier series method (FSM) to derive analytical solutions to simply supported EBBo2PF. The FSM has the advantage that the sine functions used in the series are orthogonal functions that are readily differentiated. The problem simplified by orthogonalization of the series to an algebraic eigenvalue problem which was solved to obtain exact eigenvalues.

Ike [53] used Ritz variational method to derive accurate buckling load solutions of EBBo2PFs for both ends simply supported, and both ends clamped and for one end simply supported and the other end clamped. The work developed suitable polynomial shape functions that satisfied the boundary conditions considered and used them as shape functions in deriving the Ritz variational functions for minimization with respect to the undetermined parameters. Naidu and Rao [54] presented buckling solutions for uniform beams resting on two-parameter elastic foundations. Rao and Raju [55] developed analytical solutions for the vibration and buckling analysis of thin beams resting on Pasternak foundations for clamped boundary conditions.

In this work, polynomial basis functions are used in the Galerkin method to obtain approximate critical buckling load solutions of EBBo2PFs with:

(i) simply supported ends,

(ii) clamped ends, and,

(iii) one end clamped and one end simply supported.

3. Governing equation

In general, the differential equation for the buckling of Euler-Bernoulli beam resting on two-parameter foundation (EBBo2PF) is the fourth order nonhomogeneous ordinary differential equation (NODE) [50, 52, 53]:

1

\frac{d^{2}}{d x^{2}} (E I \frac{d^{2} w}{d x^{2}}) + P \frac{d^{2} w}{d x^{2}} + k_{1} w - k_{2} \frac{d^{2} w}{d x^{2}} = q (x), 0 < x \leq l,

where $x$ is the longitudinal axis of the beam, $E$ is the Young’s modulus, $I$ is the moment of inertia, $P$ is the axial force, $q (x)$ is the applied transverse load intensity, $k_{1}$ is the first modulus/parameter of the foundation, $k_{2}$ is the second modulus/parameter of the foundation.

When there is no applied transverse load on the EBBo2PF, $q (x) = 0$ , and Eq. (1) simplifies for homogeneous beams with prismatic cross-sections to the homogeneous ordinary differential equation (HODE) with constant coefficients given by Eq. (2) [50, 52, 53]:

2

E I \frac{d^{4} w}{d x^{4}} + P \frac{d^{2} w}{d x^{2}} + k_{1} w - k_{2} \frac{d^{2} w}{d x^{2}} = 0 .

Dividing Eq. (2) by $E I$ gives Eq. (3):

3

\frac{d^{4} w}{d x^{4}} + \frac{P}{E I} \frac{d^{2} w}{d x^{2}} + \frac{k_{1}}{E I} w - \frac{k_{2}}{E I} \frac{d^{2} w}{d x^{2}} = 0 .

Alternatively, Eq. (3) can be expressed as Eq. (4):

4

\frac{d^{4} w}{d x^{4}} + (β - α_{2}) \frac{d^{2} w}{d x^{2}} + α_{1} w = 0,

where:

5

β = \frac{P}{E I}, α_{1} = \frac{k_{1}}{E I}, α_{2} = \frac{k_{2}}{E I} .

4. Methodology

4.1. Galerkin variational functional (GVF)

The deflection function $w (x)$ is expressed in terms of a finite number of linear combinations of shape functions $φ_{i} (x)$ that satisfy the boundary conditions of the beam as:

6

w (x) = \sum_{i = 1}^{n} c_{i} φ_{i} (x),

where $c_{i}$ are the generalized parameters of the deflection function $w (x)$ .

The Galerkin formulation of the governing equation then becomes expressed as Eq. (7):

7

\sum_{I = 1}^{n} c_{i} \int_{0}^{l} (φ_{i}^{i v} (x) + (β - α_{2}) {φ''}_{i} (x) + α_{1} φ_{i} (x)) φ_{j} (x) d x = 0 .

Expanding Eq. (7) gives:

8

[K] {C} = 0,

where $[K]$ is the stability matrix, $\{C\}$ is the matrix of generalized parameters.

The $i j$ element of $[K]$ is denoted as $k_{i j}$ and found as:

9

k_{i j} = \int_{0}^{l} (φ_{i}^{i v} (x) + (β - α_{2}) {φ''}_{i} (x) + α_{1} φ_{i} (x)) φ_{j} (x) d x .

4.2. Shape functions for various boundary conditions

4.2.1. Case 1: simply supported EBBo2PF

For simple supports at $x = 0$ and $x = l$ as shown in Fig. 3, the boundary conditions are:

10

w (0) = w'' (0) = 0,

w (l) = w'' (l) = 0 .

Let:

11

w (x) = a_{0} + a_{1} x + a_{2} x^{2} + a_{3} x^{3} + a_{4} x^{4},

where $a_{0}$ , $a_{1}$ , $a_{2}$ , $a_{3}$ and $a_{4}$ are the polynomial constants.

Fig. 3Simply supported EBBo2PF

By differentiation:

12a

w^{'} (x) = a_{1} + 2 a_{2} x + 3 a_{3} x^{2} + 4 a_{4} x^{3},

12b

w^{''} (x) = 2 a_{2} + 6 a_{3} x + 12 a_{4} x^{2} .

Applying the boundary conditions:

12c

w (0) = a_{0} = 0,

12d

w'' (0) = 2 a_{2} = 0,

12e

w (l) = a_{1} l + a_{3} l^{3} + a_{4} l^{4} = 0,

12f

w'' (l) = 6 a_{3} l + 12 a_{4} l^{2} = 0 .

From Eq. (12f):

13

a_{3} = - 2 a_{4} l .

Then:

14

a_{1} l = - a_{4} l^{4} - a_{3} l^{3} = - a_{4} l^{4} + 2 a_{4} l^{4} = a_{4} l^{4},

a_{1} = a_{4} l^{3} .

Hence:

15

w (x) = a_{4} (l^{3} x - 2 l x^{3} + x^{4}) .

Hence a one-parameter shape function for this case of simple supports at the ends is given by Eq. (16):

16

φ_{1} (x) = x^{4} - 2 l x^{3} + l^{3} x .

4.2.2. Case 2: clamped-clamped EBBo2PF

EBBo2PF clamped at $x = 0$ , and $x = l$ , as shown in Fig. 4 is considered.

Fig. 4EBBo2PF with clamped edges

The boundary conditions are:

17

w (0) = w' (0) = 0,

w (l) = w' (l) = 0 .

Using the fourth degree polynomial in Eq. (11), the application of boundary conditions yield:

w (0) = a_{0} = 0,

w' (0) = a_{1} = 0,

w (l) = a_{2} l^{2} + a_{3} l^{3} + a_{4} l^{4} = 0,

w' (l) = 2 a_{2} l + 3 a_{3} l^{2} + 4 a_{4} l^{3} = 0 .

Solving simultaneously:

a_{3} = - 2 a_{4} l,

a_{2} = a_{4} l^{2} .

Assuming a quartic polynomial, a one-parameter deflection function can be derived using Eq. (17) as:

18

w (x) = a_{4} (x^{4} - 2 l x^{3} + l^{2} x^{2}) .

Then for this case:

19

φ_{1} (x) = x^{4} - 2 l x^{3} + l^{2} x^{2} .

4.2.3. Case 3: clamped – simply supported EBBo2PF

EBBo2PF clamped at $x = 0$ , and simply supported at $x = l$ as shown in Fig. 5 is considered.

Fig. 5EBBo2PF clamped at x=0 and simply supported at x=l

The boundary conditions are:

20

w (0) = w' (0) = 0,

w (l) = w'' (l) = 0 .

Using the fourth degree polynomial in Eq. (11), the boundary conditions yield:

w (0) = a_{0} = 0,

w' (0) = a_{1} = 0,

w (l) = a_{2} l^{2} + a_{3} l^{3} + a_{4} l^{4} = 0,

w'' (l) = 2 a_{2} + 6 a_{3} l + 12 a_{4} l^{2} = 0 .

Solving:

a_{2} = 1.5 a_{4} l^{2},

a_{3} = - 2.5 a_{4} l .

Using the boundary conditions, a one-parameter deflection function can be derived using Eq. (20) as:

21

w (x) = a_{4} (x^{4} - 2.5 l x^{3} + 1.5 l^{2} x^{2}) .

Hence:

22

φ_{1} (x) = x^{4} - 2.5 l x^{3} + 1.5 l^{2} x^{2} .

4.3. One-Parameter GVF

Here:

23

w (x) = c_{1} φ_{1} (x) .

Then the GVF is:

24

\int_{0}^{l} (c_{1} φ_{1}^{i v} (x) + (β - α_{2}) c_{1} {φ''}_{1} (x) + c_{1} {α''}_{1} φ_{1} (x)) φ_{1} (x) d x = 0 .

Eq. (24) is simplified by factoring out $c_{1}$ to give:

24a

c_{1} \{\int_{0}^{l} (φ_{1}^{i v} (x) φ_{1} (x) + (β - α_{2}) {φ''}_{1} (x) φ_{1} (x) + α_{1} φ_{1}^{2} (x)) d x\} = 0 .

For non-trivial solution, $c_{1} \neq 0$ .

Hence, the buckling equation is:

24b

\int_{0}^{l} (φ_{1}^{i v} (x) φ_{1} (x) + (β - α_{2}) {φ''}_{1} (x) φ_{1} (x) + α_{1} φ_{1}^{2} (x)) d x = 0 .

Simplifying:

24c

I_{1} + (β - α_{2}) I_{2} + α_{1} I_{3} = 0,

where:

24d

I_{1} = \int_{0}^{l} φ_{1}^{i v} (x) φ_{1} (x) d x, I_{2} = \int_{0}^{l} {φ''}_{1} (x) φ_{1} (x) d x, I_{3} = \int_{0}^{l} φ_{1}^{2} (x) d x .

Solving the algebraic equation:

24e

β = \frac{P}{E I} = α_{2} - (\frac{I_{1} + α_{1} I_{3}}{I_{2}}) .

Hence:

24f

P = \frac{E I}{l^{2}} (α_{2} - (\frac{I_{1} + α_{1} I_{3}}{I_{2}})) l^{2} .

5. Results

5.1. EBBo2PF with simply supported edges

In this case:

25

I_{1} = 4.8 l^{5}, I_{2} = - \frac{204 l^{7}}{420}, I_{3} = - \frac{31 l^{9}}{630} .

Then:

26

P = \frac{E I}{l^{2}} (α_{2} l^{2} + (4.8 l^{7} + \frac{31 α_{1} l^{11}}{630}) \frac{420}{204 l^{7}}) .

Simplifying:

27

P = \frac{E I}{l^{2}} (α_{2} l^{2} + 9.882352941 + 0.101307189 α_{1} l^{4}) .

Eq. (27) can be expressed in the form:

28

P = \frac{E I}{l^{2}} F_{1} (α_{1} l^{4}, α_{2} l^{2}) .

$F_{1} (α_{1} l^{4}, α_{2} l^{2})$ is the buckling parameter. Approximately, $F_{1}$ can be expressed as:

29

F_{1} (α_{1} l^{4}, α_{2} l^{2}) = α_{2} l^{2} + 9.88235 + 0.1013072 α_{1} l^{4} .

$F_{1} (α_{1} l^{4}, α_{2} l^{2})$ is calculated and presented in Table 1 for $α_{1} l^{4} =$ 0, 1, 100, 1900, 10000 and $α_{2} l^{2} = 0$ , $0.5 π^{2}$ , $π^{2}$ , $2.5 π^{2} .$ Table 1 also presents previous values of $F_{1}$ calculated using FEM by Naidu and Rao [54] and Ike [52, 53] using Stodola-Vianello iteration method.

5.2. EBBo2PF with clamped edges

Here:

30

I_{1} = 0.8 l^{5}, I_{2} = - \frac{2 l^{7}}{105}, I_{3} = \frac{l^{9}}{630} .

Then:

31

P = \frac{E I}{l^{2}} (α_{2} l^{2} + \frac{105}{2 l^{7}} (0.8 l^{5} + \frac{α_{1} l^{9}}{630}) l^{2}) .

Simplifying:

32

P = \frac{E I}{l^{2}} (α_{2} l^{2} + 42 + \frac{α_{1} l^{4}}{12}) .

Eq. (32) can be expressed as:

33

P = \frac{E I}{l^{2}} F_{2} (α_{1} l^{4}, α_{2} l^{2}),

where:

34

F_{2} (α_{1} l^{4}, α_{2} l^{2}) = α_{2} l^{2} + 42 + \frac{α_{1} l^{4}}{12} .

$F_{2} (α_{1} l^{4}, α_{2} l^{2})$ is calculated for $α_{1} l^{4} =$ 0, 1, 100 and $α_{2} l^{2} = 0$ , $0.5 π^{2}$ , $π^{2}$ , $2.5 π^{2}$ using Eq. (34) and presented in Table 2 together with previous results by Naidu and Rao [54] and Rao and Raju [55].

5.3. Clamped-Pinned EBBo2PF

Here:

35

I_{1} = 1.8 l^{5}, I_{2} = - \frac{3 l^{7}}{35}, I_{3} = \frac{19 l^{9}}{2520},

36

P = \frac{E I}{l^{2}} (α_{2} l^{2} + \frac{35}{3 l^{7}} (1.8 l^{5} + \frac{19 α_{1} l^{9}}{2520}) l^{2}) .

Simplifying:

37

P = \frac{E I}{l^{2}} (α_{2} l^{2} + 21 + 0.087962962 α_{1} l^{4}) .

Eq. (37) can be expressed as:

38

P = \frac{E I}{l^{2}} F_{3} (α_{1} l^{4}, α_{2} l^{2}) .

Approximating:

39

F_{3} (α_{1} l^{4}, α_{2} l^{2}) = α_{2} l^{2} + 21 + 0.087963 α_{1} l^{4} .

$F_{3} (α_{1} l^{4}, α_{2} l^{2})$ is calculated for $α_{1} l^{4} =$ 0, 50, 100, $α_{2} l^{2} =$ 0, $0.5 π^{2}$ , $π^{2}$ , $2.5 π^{2}$ and presented in Table 3. Table 3 also presents previous results for EBBoWF (for $α_{2} l^{2} = 0)$ using variational iteration method (VIM) by Atay and Coskun [43] and exact solution by Wang et al. [36].

Table 1Critical buckling load parameters of a simply supported Euler-Bernoulli beam on a two-parameter elastic foundation

$α_{1} l^{4}$	$α_{2} l^{2}$
	0	0	0	0.5 $π^{2}$	0.5 $π^{2}$	0.5 $π^{2}$	$π^{2}$	$π^{2}$	$π^{2}$	2.5 $π^{2}$	2.5 $π^{2}$	2.5 $π^{2}$
	Present method	[9, 11] [52] [53]	Naidu & Rao (FEM) [54]	Present method	[9, 11] [52] [53]	Naidu & Rao (FEM) [54]	Present method	[9, 11] [52] [53]	Naidu & Rao (FEM) [54]	Present method	[9, 11] 52 53	Naidu & Rao (FEM) [54]
0	9.8824	9.8696	9.8696	14.8172	14.804	14.804	19.752	19.739	19.739	34.5564	35.544	35.544
1	9.9837	9.9709	9.9709	14.9185	14.907	14.907	19.8533	19.841	19.841	34.677	35.645	35.645
100	20.0131	20.002	20.002	24.9479	24.937	24.937	29.8827	29.871	29.871	44.6871	44.676	44.676
1900	202.3657	201.41	201.41	207.3	206.35	206.35	212.235	211.28	211.28	227.04	226.0	226.0
10,000	1022.954	1023.1	–	1027.889	1028	–	1032.8230	1032.9	–	1047.628	1047.7	–

Table 2Critical buckling load parameters of EBBo2PF clamped on both ends

$α_{1} l^{4}$	$α_{2} l^{2}$
	0	0	0	0.5 $π^{2}$	0.5 $π^{2}$	0.5 $π^{2}$	$π^{2}$	$π^{2}$	$π^{2}$	2.5 $π^{2}$	2.5 $π^{2}$	2.5 $π^{2}$
	Present study	Rao & Raju [52]	FEM [51]	Present Study	Rao & Raju [55]	FEM [54]	Present study	Rao & Raju [55]	FEM [54]	Present study	Rao & Raju [55]	FEM [54]
0	42 (6.39 %)	39.478	39.479	46.9348 (5.68 %)	44.413	44.414	51.8696 (5.11 %)	49.348	49.349	66.674 (3.93 %)	64.152	64.153
1	42.0833 (6.39 %)	39.554	39.555	47.0181 (5.68 %)	44.489	44.490	51.9529 (5.12 %)	49.424	49.425	66.7573 (3.93 %)	64.228	64.229
100	50.3333 (6.92 %)	47.077	47.077	55.2681 (6.26 %)	52.012	51.542	60.2029 (5.72 %)	56.9471	56.877	75.0073 (4.54 %)	71.751	71.681

The values in parenthesis in the present study results are percentage differences between present results and previous results by Rao and Raju [55].

Table 3Buckling load parameters of EBBo2PF with one end clamped and the other end simply supported

$α_{1} l^{4}$	$α_{2} l^{2}$
	0	0	0	0.5 $π^{2}$	$π^{2}$	2.5 $π^{2}$
	Present method	Exact [36]	Atay and Coskun [43]	Present method	Present method	Present method
0	21 (4 %)	20.1907	20.1908	25.9348	30.8696	45.674
50	25.39815 (4.58 %)	24.2852	24.2855	30.3330	35.2678	50.0722
100	29.7963 (5.26 %)	28.3066	28.3080	34.7311	39.6659	54.4703

The figures in parenthesis under the present method results are percentage differences between present results and the exact results by Wang et al. [36].

6. Discussion

In this work, Galerkin variational method has been used for the critical buckling load determination of EBBo2PF. The governing equation is a homogeneous ordinary differential equation in terms of the buckled deflection $w (x)$ . The paper presented the GVF in general form in terms of $n$ parameter shape functions which satisfy the boundary conditions.

The Galerkin method was illustrated using one-parameter shape function formulation for three cases of boundary conditions, namely:

– Both ends are simply supported,

– Both ends are clamped ends and one-end is clamped and the other end is simply supported.

In each case, the GVF reduced to an algebraic equation which is solved to find the critical buckling load in standard form in terms of buckling load parameters $F_{1} (α_{1} l^{4}, α_{2} l^{2}),$ $F_{2} (α_{1} l^{4}, α_{2} l^{2})$ and $F_{3} (α_{1} l^{4}, α_{3} l^{2})$ .

The buckling load parameters for simply supported EBBo2PF presented in Table 1 shows that the present results are almost identical to the exact results previously obtained by Ike [9, 11] and Naidu and Rao [54]. Table 2 presents critical buckling load parameters for EBBo2PF with both ends clamped, and shows that the present results differ from the results by Rao and Raju [55] by 3.93 % for $α_{2} l^{2} = 2.5 π^{2}$ , $α_{1} l^{4} = 0$ to 4.54 % for $α_{2} l^{2} = 2.5 π^{2}$ , $α_{1} l^{4} = 100.$ Comparable differences exist for other values of $α_{1} l^{4}$ and $α_{2} l^{2}$ presented.

Table 3 compares the present results for $α_{2} l^{2} =$ 0, $α_{1} l^{4} =$ 0, 50, 100 with the exact results. Table 3 shows that the present results differ from the exact results by 4 % for $α_{1} l^{4} = 0$ , $α_{2} l^{2} = 0$ , and 5.26 % for $α_{1} l^{4} = 100$ , $α_{2} l^{2} = 0 .$ The accuracy of the one-parameter Galerkin method is thus illustrated in the paper.

7. Conclusions

This paper has presented Galerkin method for solving critical buckling problems of EBBo2PF for the three cases of simply supported (SS) edges, clamped clamped (CC) edges and clamped-simply supported (CS) edges.

In conclusion:

1) The GVF simplified the problem to an algebraic eigenvalue problem.

2) One-parameter shape function formulation of the Galerkin solution for simply supported EBBo2PFs gave critical buckling load solutions that are almost identical to exact solutions.

3) One-parameter Galerkin solutions for clamped clamped EBBo2PF gave critical buckling loads that differ from the previous results by 3.93 % for $α_{2} l^{2} = 2.5 π^{2}$ , $α_{1} l^{4} = 0$ to 6.92 % for $α_{2} l^{2} = 0$ , $α_{1} l^{4} =$ 100.

4) The present one-parameter Galerkin solution for EBBo2PF with CS supports gave differences varying from 4 % for $α_{1} l^{4} = 0$ , $α_{2} l^{2} = 0$ to 5.26 % for $α_{1} l^{4} =$ 100, $α_{2} l^{2} = 0 .$

References

A. G. Dahake and Y. M. Ghugal, “A trigonometric shear deformation theory for flexure of thick beam,” Procedia Engineering, Vol. 51, 2013.

Publisher
M. Levinson, “A new rectangular beam theory,” Journal of Sound and Vibration, Vol. 74, No. 1, pp. 81–87, 1981, https://doi.org/10.1016/0.002-460x(81)90493-4

Publisher
A. S. Sayyad and Y. M. Ghugal, “Flexure of thick beams using new hyperbolic shear deformation theory,” International Journal of Mechanics, Vol. 5, No. 3, pp. 113–122, 2011.

Search CrossRef
Y. M. Ghugal and R. P. Shimpi, “A review of refined shear deformation theories for isotropic and anisotropic laminated beams,” Journal of Reinforced Plastics and Composites, Vol. 20, No. 3, pp. 255–272, 2001.

Publisher
F. Yue, “A refined model for analysis of beams on two-parameter foundations by iterative method,” Mathematical Problems in Engineering, Vol. 12, p. 5562212, 2021.

Publisher
C. C. Ike, “Fourier sine transform method for the free vibration analysis of Euler-Bernoulli beam resting on Winkler foundation,” International Journal of Darshan Institute on Engineering Research and Emerging Technologies, Vol. 7, No. 1, 2018.

Publisher
C. C. Ike, “Point collocation method for the analysis of Euler-Bernoulli beam on Winkler foundation,” International Journal of Darshan Institute on Engineering Research and Emerging Technologies, Vol. 7, No. 2, 2018.

Publisher
C. Ike, “Free vibration of thin beams on winkler foundations using generalized integral transform method,” Engineering and Technology Journal, Vol. 41, No. 11, pp. 1286–1297, Aug. 2023, https://doi.org/10.30684/etj.2023.140343.1462

Publisher
C. C. Ike, “Stodola-Vianello method for the buckling load analysis of Euler-Bernoulli beam on Pasternak Foundation,” UNIZIK Journal of Engineering and Applied Sciences, Vol. 2, No. 1, pp. 217–226, Jun. 2023.

Search CrossRef
C. C. Ike, O. A. Oguaghamba, and J. N. Ugwu, “Stodola-Vianello iteration method for the critical buckling load analysis of thin beam on two-parameter foundation with clamped ends,” in Proceedings Nigerian Institute of Electrical and Electronic Engineers (NIEEE) Nsukka Chapter, 2023.

Search CrossRef
C. C. Ike, “Eigenvalue solutions for Euler-Bernoulli beams on two-parameter foundations using Stodola-Vianello iteration method and polynomial basis functions,” Nnamdi Azikiwe University Journal of Civil Engineering, Vol. 1, No. 4, pp. 59–68, 2023.

Search CrossRef
A. D. Kerr, “Elastic and visco-elastic foundation models,” Journal of Applied Mechanics, Vol. 31, No. 3, pp. 491–498, 1964.

Publisher
A. D. Kerr, “A study of a new foundation model,” Acta Mechanica, Vol. 1, pp. 135–147, 1965.

Publisher
A. D. Kerr., “On the determination of foundation model parameters,” Journal of Geotechnical Engineering, Vol. 111, No. 11, pp. 1334–1340, 1985.

Publisher
V. Z. Vlasov and N. N. Leontiev, “Beams, plates and shells on elastic foundations,” Israel Program for Scientific Translations, Jerusalem, 1966.

Search CrossRef
R. Jones and J. Xenophontos, “The Vlasov foundation model,” International Journal of Mechanical Sciences, Vol. 19, No. 6, pp. 317–323, Jan. 1977, https://doi.org/10.1016/0020-7403(77)90084-4

Publisher
C. V. G. Vallabhan and Y. C. Das, “Parametric study of beams on elastic foundations,” Journal of Geotechnical Engineering, Vol. 114, No. 12, pp. 2072–2082, 1988.

Publisher
C. V. G. Vallabhan and Y. C. Das, “Modified Vlasov method for beams on elastic foundations,” Journal of Geotechnical Engineering, Vol. 117, No. 6, pp. 956–966, 1991.

Publisher
S. Akhazhanov, “Simplified method of calculating a beam on a two-parameter elastic foundation,” International Journal of GEOMATE, Vol. 25, No. 111, pp. 33–40, Nov. 2023, https://doi.org/10.21660/2023.111.3898

Publisher
S. B. Akhazhanov, N. I. Vatin, S. Akhmediyov, T. Akhazhanov, O. Khabidolda, and A. Nurgoziyeva, “Beam on a two-parameter elastic foundation: Simplified finite element model,” Magazine of Civil Engineering, Vol. 121, No. 5, p. 12107, 2023.

Search CrossRef
S. Akhazhanov, “Analytical solution of beams on elastic foundation,” International Journal of GEOMATE, Vol. 19, No. 73, pp. 193–200, Sep. 2020, https://doi.org/10.21660/2020.73.51487

Publisher
S. Akhazhanov, D. Baltabai, and B. Nurlanova, “Refined mechanical and mathematical model of an elastic half-plane,” Technobius, Vol. 2, No. 1, 2022.

Publisher
M. S. Huang, X. C. Zhou, J. Yu, C. F. Leung, and Q. W. T. Jorgin, “Estimating the effects of tunnelling on existing jointed pipelines based on Winkler model,” Tunnelling and Underground Space Technology, Vol. 86, pp. 89–99, 2019.

Publisher
S. Akhmediev, G. Mikhailov Tazhenova, M. Bakirov, T. Filippova, and D. Tokanov, “Calculating a beam of variable section lying on an elastic foundation,” Journal of Applied Engineering Science, Vol. 21, No. 1, pp. 87–93, 2023.w

Publisher
J. M. Zhang, Y. J. Shang, and R. Y. Wang, “Force analysis method of buried pipeline in landslide section based on Pasternak double parameter model,” Journal of Central South University (Science and Technology Edition), Vol. 51, No. 5, pp. 1328–1336, 2020.

Search CrossRef
M. Gholami and M. Alizadeh, “A quasi-3D modified strain gradient formulation for static bending of functionally graded micro beams resting on Winkler-Pasternak elastic foundation,” Scientia Iranica, Vol. 29, No. 1, pp. 26–40, 2022.

Publisher
P. Gulkan and B. N. Alemdar, “An exact finite element for a beam on a two-parameter elastic foundation: a revisit,” Structural Engineering and Mechanics, Vol. 7, No. 3, pp. 259–276, Mar. 1999, https://doi.org/10.12989/sem.1999.7.3.259

Publisher
I. B. Teodora and V. Musat, “Beam elements on linear variable two-parameter elastic foundation,” Bulletinul Institutului Politehnic dini lasi, Vol. 54, No. 2, pp. 69–78, 2008.

Search CrossRef
R. Alzubaidi, H. M. Husain, and S. Shukur, “Finite element analysis of beam resting on footing,” International Journal of Geomate, Vol. 24, No. 105, pp. 26–32, 2023.

Publisher
Z. Więckowski and P. Świątkiewicz, “Stress-based FEM in the problem of bending of Euler-Bernoulli and timoshenko beams resting on elastic foundation,” Materials, Vol. 14, No. 2, p. 460, Jan. 2021, https://doi.org/10.3390/ma14020460

Publisher
A. Worku and B. Habte, “Analytical formulation and finite element implementation technique of a rigourous two-parameter foundation model to beams on elastic foundations,” Geomechanics and Geoengineering, Vol. 17, No. 2, pp. 547–566, 2022.

Publisher
O. T. Olotu, O. O. Agboola, and J. A. Gbadeyan, “Free vibration analysis of non-uniform Rayleigh beams on variable Winkler elastic foundation using differential transform method,” Ilorin Journal of Science, Vol. 8, No. 1, pp. 1–20, Jun. 2021, https://doi.org/10.54908/iljs.2021.08.01.001

Publisher
M. Aslami and P. A. Akimov, “Analytical solution for beams with multipoint boundary conditions on two-parameter elastic foundations,” Archives of Civil and Mechanical Engineering, Vol. 16, No. 4, pp. 668–677, Sep. 2016, https://doi.org/10.1016/j.acme.2016.04.005

Publisher
M. Hetenyi, “Beams on elastic foundation: Theory with applications in the field of Civil and Mechanical Engineering,” University of Michigan Press, Ann Arbor, 1946.

Search CrossRef
S. P. Timoshenko and J. M. Gere, Theory of Elastic Stability. McGraw-Hill International, 1985.

Search CrossRef
C. M. Wang and C. Y. Wang, Exact Solutions for Buckling of Structural Members. Florida: CRC Press, 2004, https://doi.org/10.1201/9780203483534

Publisher
M. H. Taha and S. A. Hadima, “Analysis of non-uniform beams on elastic foundations using recursive differentiation method,” Engineering Mechanics, Vol. 22, pp. 83–94, 2015.

Search CrossRef
M. H. Taha., “Recursive differentiation method of beams for boundary value problems: application to analysis of a beam-column on an elastic foundation,” Journal of Theoretical and Applied Mechanics Sofia, Vol. 44, No. 2, pp. 57–70, 2014.

Publisher
M. Soltani, “Finite element modeling for buckling analysis of tapered axially functionally graded timoshenko beam on elastic foundation,” Mechanics of Advanced Composite Structures‎, Vol. 7, No. 2, Nov. 2020, https://doi.org/10.22075/macs.2020.18591.1223

Publisher
J. D. Aristizabal-Ochoa, “Stability of slender columns on an elastic foundation with generalized end conditions,” Ingenieria Investigacion, Vol. 33, No. 3, pp. 34–40, 2013.

Publisher
M. Hassan, “Buckling of beams on elastic foundations,” Al Rafidain Engineering Journal, Vol. 16, pp. 104–122, 2008, https://doi.org/10.33899/rengj.20.44659

Publisher
V. Anghel and C. Mares, “Integral formulation for stability and vibration analysis of beams on elastic foundation,” Proceedings of the Romanian Academy Series A, Vol. 20, No. 3, pp. 285–293, 2019.

Search CrossRef
M. T. Atay and S. B. Coşkun, “Elastic stability of Euler columns with a continuous elastic restraint using variational iteration method,” Computers and Mathematics with Applications, Vol. 58, No. 11-12, pp. 2528–2534, Dec. 2009, https://doi.org/10.1016/j.camwa.2009.03.051

Publisher
B. Akgoz, K. Mercan, C. Demir, and O. Civalék., “Static analysis of beams on elastic foundation by the method of discrete singular convolution,” International Journal of Engineering and Applied Sciences, Vol. 8, No. 3, pp. 67–73, 2016.

Publisher
C. C. Ike, E. U. Ikwueze, and I. O. Ofondu., “Picard’s successive iteration method for the elastic buckling analysis of Euler columns with pinned ends,” Saudi Journal of Civil Engineering, Vol. 2, No. 2, pp. 76–88, 2018.

Search CrossRef
I. O. Ofondu, E. U. Ikwueze and C. C. Ike, “Determination of the critical buckling loads of Euler columns using Stodola-Vianello iteration method,” Malaysian Journal of Civil Engineering, Vol. 30, No. 3, pp. 378–394, Nov. 2018, https://doi.org/10.11113/mjce.v30.16064

Publisher
E. U. Ikwueze, C. C. Ike, and I. O. Ofondu., “Least squares weighted residual method for the elastic buckling analysis of Euler column with fixed pinned ends,” Saudi Journal of Civil Engineering, Vol. 2, No. 2, pp. 110–119, 2018.

Search CrossRef
B. O. Mama, O. A. Oguaghamba, and C. C. Ike., “Quintic polynomial shape functions for the finite element analysis of elastic buckling loads of Euler-Bernoulli beams resting on Winkler foundation,” in Proceedings 2nd Nigerian Institute of Electrical and Electronic Engineers Nsukka Chapter Conference, 2020.

Search CrossRef
C. C. Ike, O. A. Oguaghamba, and J. N. Ugwu, “Stodola-Vianello iteration method for the critical buckling load analysis of thin beam on Winkler foundation with clamped end,” in Proceedings Nigerian Institute of Electrical and Electronic Engineers (NIEEE) Nsukka Chapter, 2023.

Search CrossRef
C. C. Ike, “Critical buckling load solution of thin beam on Winkler foundation via polynomial shape function in Stodola-Vianello iteration method,” Journal of Research in Engineering and Applied Sciences, Vol. 8, No. 3, pp. 591–595, Jul. 2023.

Publisher
C. C. Ike, “Stodola-Vianello method for the buckling load analysis of Euler-Bernoulli beam on Winkler foundation,” UNIZIK Journal of Engineering and Applied Sciences, Vol. 2, No. 1, pp. 250–259, 2023.

Search CrossRef
C. C. Ike, “Fourier series method for the stability solution of simply supported thin beams on two-parameter elastic foundations of the Pasternak, Filonenko-Borodich, Hetenyi or Vlasov models,” Journal of Engineering and Thermal Sciences, Vol. 4, No. 1, pp. 30–45, Jun. 2024, https://doi.org/10.21595/jets.2024.23913

Publisher
C. Ike, “Ritz variational method for buckling analysis of Euler-Bernoulli beams resting on two-parameter foundations,” Iraqi Journal of Civil Engineering, Vol. 18, No. 1, pp. 26–49, Jun. 2024, https://doi.org/10.37650/ijce.2024.180103

Publisher
N. R. Naidu and G. V. Rao, “Stability behaviour of uniform beams on a class of two-parameter elastic foundation,” Computers and Structures, Vol. 57, No. 3, pp. 551–553, 1995.

Publisher
G. V. Rao and K. K. Raju, “Elegant and accurate closed form solutions to predict vibration and buckling behaviour of slender beams on Pasternak foundation,” Indian Journal of Engineering and Materials Science, Vol. 9, pp. 98–102, 2002.

Search CrossRef

About this article

Received

27 June 2024

Accepted

03 September 2024

Published

15 October 2024

DOI

https://doi.org/10.21595/jmai.2024.24285

Keywords

Galerkin variational method

Euler-Bernoulli beam

two-parameter elastic foundation

critical buckling load

shape function

Acknowledgements

The authors have not disclosed any funding.

Data Availability

The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

Conflict of interest

The authors declare that they have no conflict of interest.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Research article

2018 09 30

Analytical solution for modal analysis of Euler-Bernoulli and Timoshenko beam with an arbitrary varying cross-section

Fatemeh Sohani, H. R. Eipakchi

Research article

2016 05 15

Nonlinear free vibration analysis of nanobeams under magnetic field based on nonlocal elasticity theory

Tai-Ping Chang

Research article

2015 06 30

Primary resonance of a rotating composite shaft with geometrical nonlineary

Yongsheng Ren, Yuhuan Zhang, Qiyi Dai, Xingqi Zhang

Research article

2014 11 15

Transverse vibration analysis of an axially moving beam with lumped mass

Ning Liu, Guolai Yang, Bo Chen

C. C. Ike, “Critical buckling load analysis of Euler-Bernoulli beam on two-parameter foundations using Galerkin method,” Journal of Mechatronics and Artificial Intelligence in Engineering, Vol. 5, No. 2, –14, Oct. 2024, https://doi.org/10.21595/jmai.2024.24285

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jmai.2024.24285
UR  - https://doi.org/10.21595/jmai.2024.24285
TI  - Critical buckling load analysis of Euler-Bernoulli beam on two-parameter foundations using Galerkin method
T2  - Journal of Mechatronics and Artificial Intelligence in Engineering
AU  - Ike, Charles Chinwuba
PY  - 2024
DA  - 2024/10/15
PB  - Extrica
VL  - 5
IS  - 2
SN  - 2669-1116
ER  - 

Copy Ris

Copied to clipboard!

 @article{Ike_2024, title={Critical buckling load analysis of Euler-Bernoulli beam on two-parameter foundations using Galerkin method}, ISSN={2669-1116}, url={https://doi.org/10.21595/jmai.2024.24285}, DOI={10.21595/jmai.2024.24285}, journal={Journal of Mechatronics and Artificial Intelligence in Engineering}, publisher={JVE International Ltd.}, author={Ike, Charles Chinwuba}, year={2024}, month=oct }

Copy Bibtex

Copied to clipboard!

[1]C. C. Ike, “Critical buckling load analysis of Euler-Bernoulli beam on two-parameter foundations using Galerkin method,” Journal of Mechatronics and Artificial Intelligence in Engineering, Oct. 2024, doi: 10.21595/jmai.2024.24285.

Copy IEEE

Copied to clipboard!

Ike, Charles Chinwuba. “Critical Buckling Load Analysis of Euler-Bernoulli Beam on Two-Parameter Foundations Using Galerkin Method.” Journal of Mechatronics and Artificial Intelligence in Engineering, October 15, 2024. https://doi.org/10.21595/jmai.2024.24285.

Copy Chicago

Copied to clipboard!

Critical buckling load analysis of Euler-Bernoulli beam on two-parameter foundations using Galerkin method

Abstract

Highlights

1. Introduction

2. Literature review

3. Governing equation

4. Methodology

4.1. Galerkin variational functional (GVF)

4.2. Shape functions for various boundary conditions

4.2.1. Case 1: simply supported EBBo2PF

4.2.2. Case 2: clamped-clamped EBBo2PF

4.2.3. Case 3: clamped – simply supported EBBo2PF

4.3. One-Parameter GVF

5. Results

5.1. EBBo2PF with simply supported edges

5.2. EBBo2PF with clamped edges

5.3. Clamped-Pinned EBBo2PF

6. Discussion

7. Conclusions

References

About this article

Related Articles