Stress state and strength of welded joints with V-shaped elements

1. Introduction

Ensuring the safety and reliability of main pipeline systems in Russia is given special attention due to their importance for the country's economy, large total length, significant degree of wear and tear, and variety of operating conditions. In solving this problem, a special place is occupied by methods for monitoring the technical condition of pipelines, methods for assessing the danger of detected defects, as well as methods for repairing defective areas. Meanwhile, in each of these areas there are a number of unsolved problems that require improvement of the methodological base.

The reasons for the imperfection of calculation methods are as follows:

– Discrepancy between the set of parameters measured during pipeline inspection and those required to perform calculations. For example, the shapes and sizes of half of the total number of defects detected during in-line diagnostics remain unknown. This is especially noticeable in welding defects. Thus, features of the type “anomaly on the weld” are identified during assessments as a welded joint with offset edges [1]. At the same time, all dimensions of this weld remain unknown, including the size of the offset, the angle and radius of the transition from the weld metal to the pipe surface. Meanwhile, the stress concentration on joints with offset edges depends primarily on these parameters.

– Imperfection of calculation methods for some types of defects. For example, for the same welded joints with offset edges, calculation methods are usually used based on the approaches of classical mechanics (strength of materials) using the concept of “stress concentration factor” [2]. At the same time, the very value of the stress concentration coefficient remains unknown, since one of the main initial parameters is unknown – the radius of the transition from the weld to the base metal [3]. Therefore, a simplified approach is often used, using the concept of “minimum cross-section”, that is, without taking into account the phenomenon of stress concentration.

The strength of joints with offset edges is determined by the V-shaped stress raiser, which is formed by a sharp transition from the weld metal to the base metal. Similar V-shaped stress concentrators appear on all welded joints with fillet welds [4]. Therefore, the reliability of repair structures (patches, couplings) used in the repair of defective sections of pipelines is entirely determined by the patterns of stress formation at V-shaped concentrators, which are the transitions from the seam to the base metal of the pipe.

The danger of V-shaped stress concentrators on welded joints is determined by the radius of transition from the weld to the base metal. However, this parameter is a random variable. Therefore, in assessing strength and durability, it is advisable to take the transition radius equal to zero, i.e. consider the V-shaped concentrator sharp [5].

All “risk” type defects detected during in-line diagnostics of pipelines should also be considered V-shaped stress concentrators. The danger of these defects depends on their depth and sharpness (radius of curvature at the apex) [6]. Since the radius of curvature of such defects remains uncertain, it should be taken equal to zero in calculations.

Thus, there is a need to develop a theory of the stress state and strength of pipeline elements with sharp V-shaped stress concentrators.

2. Features of inspection of defective welded joints and methods for assessing their strength

Special attention is currently being paid to the development of pipeline diagnostic methods. A special place is occupied by in-pipe diagnostic methods, which make it possible to identify and measure a significant number of defects in main pipelines almost without stopping pipeline operation. According to experts, through the consistent use of in-pipe flaw detectors with sensors of different operating principles (mechanical, ultrasonic, magnetic, navigation), it is possible to detect up to 90 % of pipe defects and up to 40,..., 50 % of welded joint defects. However, some types of defects (pores, undercuts, most small cracks) remain undetected due to insufficient sensitivity and resolution of the instruments. As a result, welded joints account for up to half of all pipeline failures. The picture of welded joints becomes more complicated due to the fact that they concentrate several factors that negatively affect their strength and service life.

Firstly, welded joints are almost always heterogeneous in geometric shapes and sizes. Welded joints are characterized by such features as convexity (strengthening), concavity (weakening), angularity (fillet weld), displacement of edges, undercut, slag inclusions, lack of penetration. All these features lead to the formation of stress concentrations in local areas, which negatively affects the strength and safety of the pipeline.

Secondly, welded joints are characterized by mechanical heterogeneity. The weld metal, heat-affected zone and base metal differ from each other in their mechanical properties: yield limits, strength, fatigue, crack resistance. This also leads to a distortion of the stress-strain state of the section, which is especially noticeable on highly loaded pipelines.

Thirdly, in welded joints there are always residual welding stresses caused by the welding technology itself. These stresses, superimposed on the stresses from operating and associated loads, also lead to overstresses in individual zones and thereby reduce the strength and service life of the pipeline as a whole.

To fully take into account all these features when assessing the strength, especially after long-term operation of pipelines, is a rather difficult task. The existing regulatory framework of the industry does not always reflect these features, and, as we see it, for the following two reasons.

1. The control methods used do not allow measuring some important characteristics of mechanical and geometric heterogeneity, as well as residual stresses in the areas of welded joints.

2. The methods used for assessing strength are based on classical concepts and are not always based on modern achievements in fracture mechanics.

3. Discrepancy between the type and volume of information obtained during pipeline inspection and the volume and type of information necessary to perform full-fledged calculations.

For example, during in-line diagnostics, almost all defects in welded joints are marked as a “weld anomaly.” The anomaly can be caused by displacement of the edges, the presence of undercuts, lack of fusion, inclusions, altered metal structure and other reasons. If the anomaly is caused by displacement of the edges, then a V-shaped section will necessarily appear there, formed at the transition from the weld metal to the base metal of the pipe. However, such important weld parameters as the displacement size, radius and angle of transition from the weld metal to the pipe surface remain unknown. This, in turn, affects the choice of calculation methods. For example, for the same welded joints with offset edges with a V-shaped surface area, calculation methods based on the concepts of “stress concentration factor” or “stress intensity factor” can be used [7, 8]. However, the values of these coefficients cannot be determined, since the most important initial parameters remain unknown - the angle and radius of the transition from the weld to the base metal. Therefore, a simplified approach based on the concept of “minimum cross-section” is often used, without fully taking into account the phenomenon of stress concentration. In our opinion, in such cases (under conditions of uncertainty) it is necessary to calculate welded joints using the worst case scenario (with a margin), taking the radius of transition from the seam to the pipe surface to be zero. But for this it is necessary to improve the approaches of fracture mechanics, which until now have been applied mainly only to cracks [9].

The relevance of this task increases with the increase in the volume of repair work on pipelines due to the natural processes of aging and wear. The scope of repairs is determined based on the results of periodic inspections. When repairing defective areas, reinforcing elements are often used: welded pads and couplings of various designs. When installing such elements, fillet welds inevitably appear, which are stress concentrators due to the presence of V-shaped sections (transitions from the weld metal to the pipe metal). Consequently, here too it is necessary to take into account not only the legs of the weld, but also such parameters as the transition radius and the transition angle. The current calculation standards do not take them into account; therefore, important features that determine stress concentration remain unattended.

All this requires special research aimed at studying V-shaped elements on pipelines and other structures, identifying patterns in the formation of stress concentrations, and developing special calculation methods using not only classical approaches, but also approaches from fracture mechanics.

3. Method for assessing the level of stress state of welded joints with defects

Assessment of the level of stress-strain state of welded joints with defects is carried out in 3 stages:

Stage 1: assessment of the total stress-strain state of the pipeline in order to determine mechanical stresses (circular, longitudinal and intensity) near the weld section.

The calculation of the nominal stress-strain state comes down to determining: the total nominal longitudinal stresses are determined in accordance with the requirements of [10]. Voltages are determined from all standard loads.

The calculated nominal longitudinal stresses during operation for straight and elastically curved sections of underground and above-ground (in the embankment) main pipelines in the absence of longitudinal and transverse movements, subsidence and soil heaving are determined by the formulas:

where ${\sigma }_{\theta }^{N,s}$ – hoop stress from standard (working) pressure, MPa; $\nu$ – Poisson’s ratio of the pipe metal; $E$ – Young’s modulus of the pipe metal, MPa; $p$ – standard (working) gas pressure, MPa; $D_{out}$ – outer diameter of the pipeline, m; $D_{int}=(D_{out}-2t)$ – internal diameter of the pipeline, m; $t$ – pipe wall thickness, m; ${\alpha }_T$ – coefficient of linear thermal expansion of pipe metal, 1/deg.; $\mathrm{\Delta }T$ – calculated temperature difference, determined in accordance with [10] and taken positive when heating, degrees; $\rho$ – minimum radius of elastic bending of the pipeline axis, m.

Stage 2: determination of stress concentration through calculation of stress concentration coefficients.

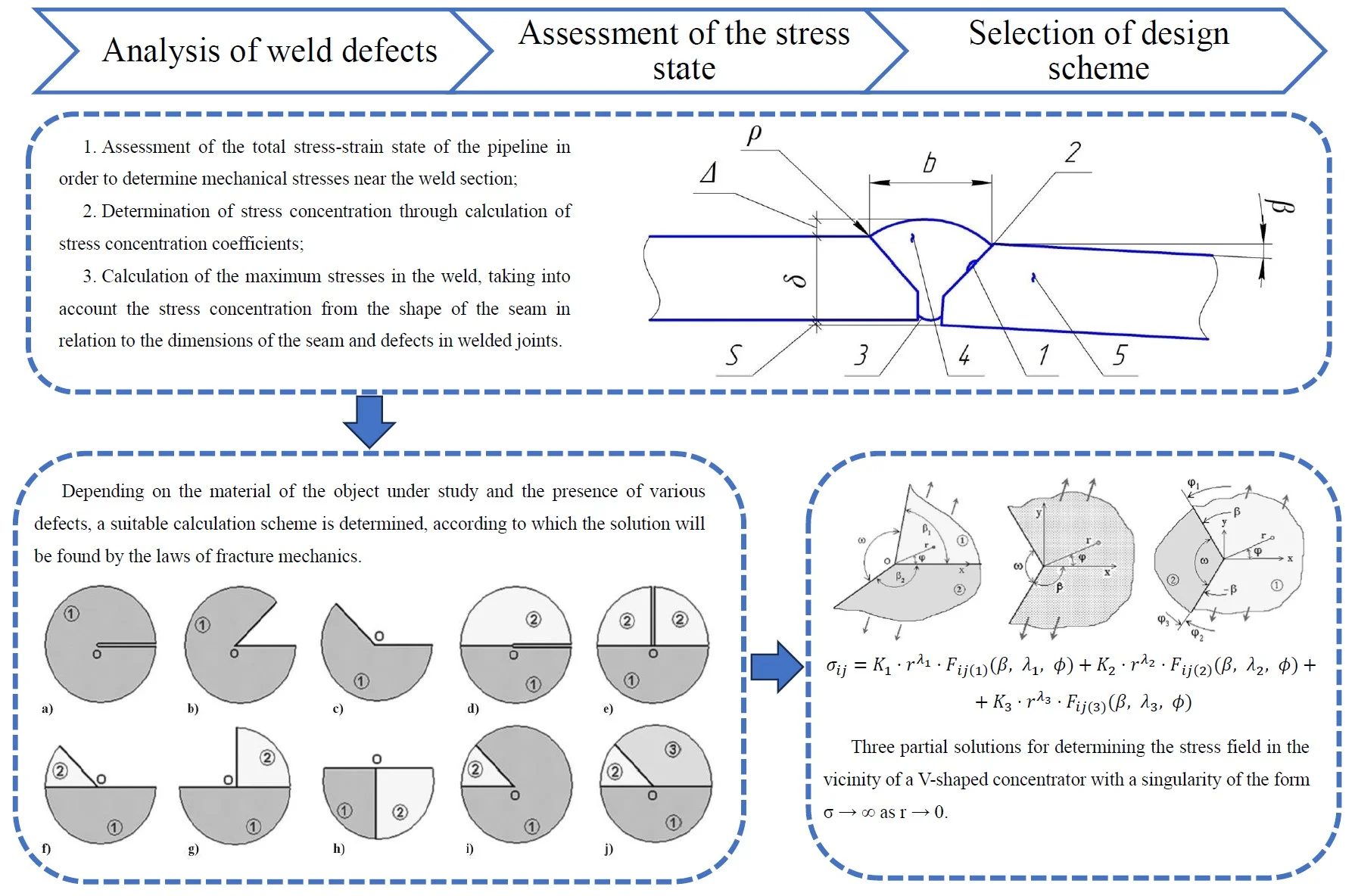
The effect of stress concentration occurs in the section with a defect. Mechanical stresses increase abruptly in comparison with the nominal stress in a defect-free weld. The reason is a decrease in the working cross-sectional area and a change in the geometric shape of the weld (Fig. 1).

Fig. 1geometric deviations and other weld defects: S – lateral displacement; β – angular displacement; ρ – radius of transition from the weld to the pipe; Δ – height of weld reinforcement; δ – pipe wall thickness; b – width of the weld; 1 – lack of fusion of edges; 2 – undercut; 3 – lack of penetration; 4 – seam crack; 5 – crack in the heat-affected zone

Theoretical stress concentration factors can be classified as follows:

1. Weld defects of butt origin:

where ${\alpha }_s$– weld shape coefficient; ${\alpha }_g$ – coefficient of geometric deviations; ${\alpha }_u$ – coefficient of undercut of the welded joint:

where $\rho$ – radius of transition from the weld to the pipe; $\delta$ – pipe wall thickness; $b$ – width of the weld; $\mathrm{\Delta }$ – height of weld reinforcement:

where $s$ – radial displacement of the edges of the welded joint; $\beta$ – angularity of the weld, degrees; $\gamma =(D_{max}-D_{min})/D$ – parameter taking into account the ovality of the pipe; $D$, $D_{max}$, $D_{min}$ – nominal, maximum and minimum values of the outer diameter of the pipe, respectively; $R=D/2$ – pipe radius; $\mu$, $E$ – Poisson’s ratio and elastic modulus of steel, respectively; $p$ – working pressure in the pipeline:

where $a$ – undercut depth; $\rho$ – radius at the vertex of the undercut.

2. Corrosion ulcers:

where $d$ – diameter of the ulcer; $b$ – ulcer depth.

3. Mechanical risks, scratches, cuts and burrs, characterized by length $l$, width $d$, depth $b$ and radius of curvature at the apex for a pipe with wall thickness $\delta$.

Long defects ($l>10d$):

– for $b\le \delta /2$:

– for $b>\delta /2$:

Short defects ($d<1<10d$):

4. Pipe wall dents:

where $b$ – depth of the dent; $\delta$ – pipe wall thickness; $d$ – dent diameter; $D_{out}$ – outer diameter of the pipe.

Scope of application of the formula:

Stage 3: calculation of the maximum stresses in the weld, taking into account the stress concentration from the shape of the seam in relation to the dimensions of the seam (width of the reinforcing bead, height, thickness of the gas pipeline wall) and defects in welded joints.

For classical defects (with a finite radius of curvature at the tip), the stress stress measure is ${\alpha }_{\sigma }$ – the theoretical stress stress coefficient, calculated under the assumption that the pipe is in an elastic state, including the defect zone. The parameter ${\alpha }_{\sigma }$ is related to voltage as follows:

where ${\sigma }_{max}$ – maximum stress at the top of the defect; ${\sigma }_{netto}$ – average stress in the netto section.

The ${\sigma }_{netto}$ value is related to the rated voltage as follows:

where $h$ – normal pipe wall thickness; $d$ – depth of damage or defect; $\left(h-d\right)$ – residual wall thickness.

If in-line diagnostic data and diagnostic examination of various defects are available, stress concentration coefficients are calculated and the actual stress values are found.

4. Application of fracture mechanics in problems of assessing the strength of welded joints with V-shaped elements

As is known, the main merit of fracture mechanics is that it provided a tool for the study of cracks [8]. If a crack is considered as a defect with a zero radius of curvature at the tip, then, according to the laws of elasticity theory, the stresses in the vicinity of the crack tip obey the expression $\sigma ~K/\sqrt{r}$ , where $K$ is a coefficient depending on the load; $r$ – distance from crack tips. Then it turns out that the stresses in the vicinity of the crack tip tend to infinity ($\sigma \to \infty$ as $r$ → 0) for any value of the coefficient $K\ne$ 0. Consequently, under any load, the stress at the crack tip will exceed any given value of the ultimate strength ${\sigma }_U$. It follows that any crack should lead to the destruction of any structure under any load, even one made of the strongest material.

This paradox in fracture mechanics was resolved by introducing a new fracture criterion – the limiting value of the coefficient $K$, which was called the crack resistance limit of the $K_{IC}$ material, similar to other limits: yield, strength, fatigue. The introduced criterion has different names, the most common of which is fracture toughness.

However, the problems with the introduction of the new criterion did not end. One of these problems is the complex dimension of the crack resistance limit. Another is the relationship between $K_{IC}$ and other fundamental strength characteristics of materials.

Research has shown that a singularity of the form $\sigma \to \infty$ can arise not only on cracks, but also in other cases. One such case is V-shaped elements with zero radius at the apex [11]-[13]. The welded elements mentioned above refer to such a case. In them, V-shaped elements can be considered as cracks opened to a certain angle $\omega >$0 (in the case of a crack $\omega =$0). It turned out that in this case the expression $\sigma ~K/\sqrt{r}$ is transformed into the expression $\sigma ~K/r^{\gamma }$, where the degree of $\gamma$ depends on the opening angle $\omega$. Accordingly, all other characteristics undergo transformation, and even the dimension of the coefficient $K$, and at the same time the dimension of its critical value. It turns out that for each angle $\omega$ it is necessary to introduce its own strength criterion. But the strength criteria should not be limited to the maximum values of the coefficient $K$ at any one value of the angle $\omega$, but should be more fundamental. Determining such fundamental criteria is also an important problem, without solving which it is impossible to move forward.

With the use of new structural materials, composites, with the development of welding, soldering, gluing technologies, etc. Other cases of singularity of the type $\sigma \to \infty$ also appeared. In this case, a factor of heterogeneity of the structural element in terms of mechanical properties appears.

We also note that the materials themselves have a complex structure. Similar to microcracks, the sizes of which are comparable to the sizes of grains in the microstructure of metals, inside steels there are V-shaped elements of the same size. They are formed at grain boundaries, the crystal lattices of which have different orientations. In the vicinity of such elements, internal stress fields are formed, which, under certain conditions, lead to the formation and development of microcracks. Thus, fracture mechanics can be extended, with some limitations, to the area of metal microstructure, thereby providing explanations for some of the distinctive properties of fine-grained metals from coarse-grained ones, and composite materials from traditional metals. By studying the patterns of formation of stress concentrations in the microstructure of materials, one can come to an understanding of a number of phenomena, for example, how grain growth in metals affects their strength, brittleness, crack resistance, and also provide an explanation for the phenomenon of accumulation of damage under cyclic loads.

Thus, the class of singular problems has expanded significantly, and the crack studied in fracture mechanics has become only one simplest special case. However, the crack itself also expanded its circle.

So, we list some cases of the occurrence of singular stress fields:

1) A crack in a homogeneous material (the subject of the study of fracture mechanics).

2) A crack at the junction of two different materials (interfacial crack).

3) A crack crossing the boundary of two different materials.

4) V-shaped element in a homogeneous material.

5) Composite V-shaped element (the element consists of two or several sectors occupied by different materials).

6) Edge joint zone in the connection of two materials.

7) Foreign inclusions in the structure of the material.

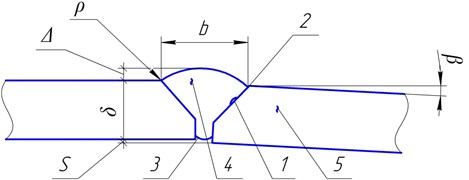
It seems to us that all these cases can be combined with a single approach based on the achieved successes in fracture mechanics, and consider the calculation schemes shown in Fig. 2. Moreover, each previous scheme can be considered as a special case of subsequent tasks. This, on the one hand, will make it possible to consider previous cases as test cases when solving subsequent problems, and secondly, it will make it possible to better understand the new patterns obtained.

Fig. 2Elements that form the singularity of a species: a) crack in homogeneous material; b), c) V-shaped elements in a homogeneous material; d) interfacial crack; e) crack crossing the boundary materials section; f), g) mechanically heterogeneous V-shaped elements; h) the edge zone of the junction of two different materials; i), j) – inclusions in the microstructure of materials

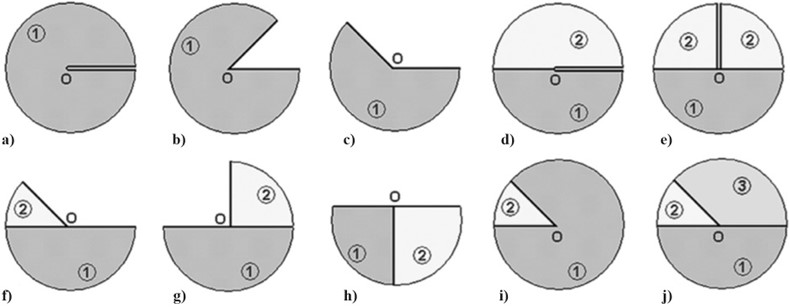
To study stress fields in the vicinity of sharp V-shaped concentrators, the Kolosov-Muskhelishvili method of complex potentials was used in combination with the “microscope principle” formulated by S.M. Belonosov and developed G. P. Cherepanov [8]. The essence of this principle is that if the model configuration does not change when the scale increases, then the complex potentials should be selected from the class of power functions. The calculation model and boundary conditions fully correspond to this condition (Fig. 3).

The solution showed that the general stress field in the vicinity of a V-shaped concentrator is decomposed into an infinite series of terms, of which only three describe the stress concentration and create a singularity of the form $\sigma \to \infty$ as $r\to 0$. These particular solutions have the following form:

where $K_1$, $K_2$, $K_3$ are stress intensity factors in the area of the top of the V-shaped concentrator; ${\lambda }_1$, ${\lambda }_2$, ${\lambda }_3$ – parameters of the stress field feature, which depend only on the opening angle $\omega$.

Functions of the type $F_{ij}(\beta ,\lambda ,\varphi )$ describe the dependence of the stress components ${\sigma }_{ij}$ on the polar angle $\phi$ for given parameters $\beta$ and $\lambda$.

Fig. 3Design diagrams of V-shaped elements

Of interest here are the dependences of the parameters ${\lambda }_1$, ${\lambda }_2$, ${\lambda }_3$ on the opening angle $\omega$ and on the ratio of the mechanical characteristics of the materials forming the V-shaped element. In the case of a crack (at $\omega \to 0$), all parameters ${\lambda }_1$, ${\lambda }_2$, ${\lambda }_3$ become equal to the same value – 0.5. In this case, the dimensions of all SIFs also become the same $\left[K_1\right]=\left[K_2\right]=\left[K_3\right]=Pа\bullet m^{\mathrm{0,5}}=\frac{N}{m^{\mathrm{1,5}}}$. This made it possible in fracture mechanics to introduce an artificial parameter of the same dimension – fracture toughness $K_{IC}$ – and take it as a characteristic of the strength of a material in the presence of a crack.

In the case of a V-shaped element, a complex situation generally arises. Firstly, all particular solutions can lead to a stress field singularity. Therefore, fracture mechanics approaches based on comparison of SIF values with fracture toughness $K_{IC}$ should be applied to them. But this is impossible to do, since they have different dimensions. For example, for the case $\omega =$60 °С we have ${\lambda }_1=$–0.48778; ${\lambda }_2=$–0.2691; ${\lambda }_3=$–0.4. Moreover, from Eq. (20) we obtain $\left[K_1\right]=Pa\bullet m^{{-\lambda }_1}=\frac{N}{m^2}\bullet m^{\mathrm{0,48778}}=\frac{N}{m^{\mathrm{1,51222}}}$. Likewise, $\left[K_2\right]=Pa\bullet m^{{-\lambda }_2}=\frac{N}{m^2}\bullet m^{\mathrm{0,2691}}=\frac{N}{m^{\mathrm{1,7309}}}$; $\left[K_3\right]=Pa\bullet m^{{-\lambda }_3}=\frac{N}{m^2}\bullet m^{\mathrm{0,4}}=\frac{Н}{m^{\mathrm{1,6}}}$; $\left[K_{1C}\right]=\frac{N}{m^{\mathrm{1,5}}}$. As we can see, the resulting dimensions are completely different, which do not allow us to evaluate the strength of a structural element (welded joint) with a V-shaped stress raiser by comparing these coefficients. Thus, it is impossible to remain within the framework of the classical theory of strength due to the singularity $\sigma \to \infty$; and we cannot use conventional approaches of fracture mechanics due to the disproportion between the SIF and the fracture toughness.

For such cases, a number of new and well-known destruction criteria have been developed:

− Simplified force criterion $K_1<K_1^{*}$; $K_1^{*}={\sigma }_U\bullet {\left(\frac{K_{IC}}{{\sigma }_U\sqrt{2\pi }}\right)}^{-2{\lambda }_1}$.

− Generalized force criterion, taking into account several SIFs with different dimensions; ${\left(\frac{K_1}{K_1^{*}}\right)}^2+{\left(\frac{K_2}{K_2^{*}}\right)}^2+\left(\frac{K_3}{K_3^{*}}\right)<1$; $K_2^{*}={\sigma }_U\bullet {\left(\frac{K_{IC}}{{\sigma }_U\bullet \sqrt{2\pi }}\right)}^{-2{\lambda }_2}$; $K_3^{*}={\sigma }_U\bullet {\left(\frac{K_{IC}}{{\sigma }_U\bullet \sqrt{2\pi }}\right)}^{-2{\lambda }_3}$.

− Energy criterion $G_0\le G_C$.

− Criterion of equivalent crack $h_{eq}$.

− Local deformation-force criterion.

− Empirical criterion based on the singularity parameter $\lambda$.

− Failure criteria for mechanically inhomogeneous elements ($K$-approach, energy method, equivalent crack method).

5. Conclusions

Previously, fracture mechanics had limited application in the oil and gas industry; mainly when analyzing the stress state around cracks and crack-like defects – lack of fusion in welds. The solutions obtained in the work can be used in analyzing the stress state and strength of welded joints with sharp transitions from the seam to the base metal of the pipe.