Modal characteristics analysis of agricultural vehicle support frame

2.1. The establishment of finite element model

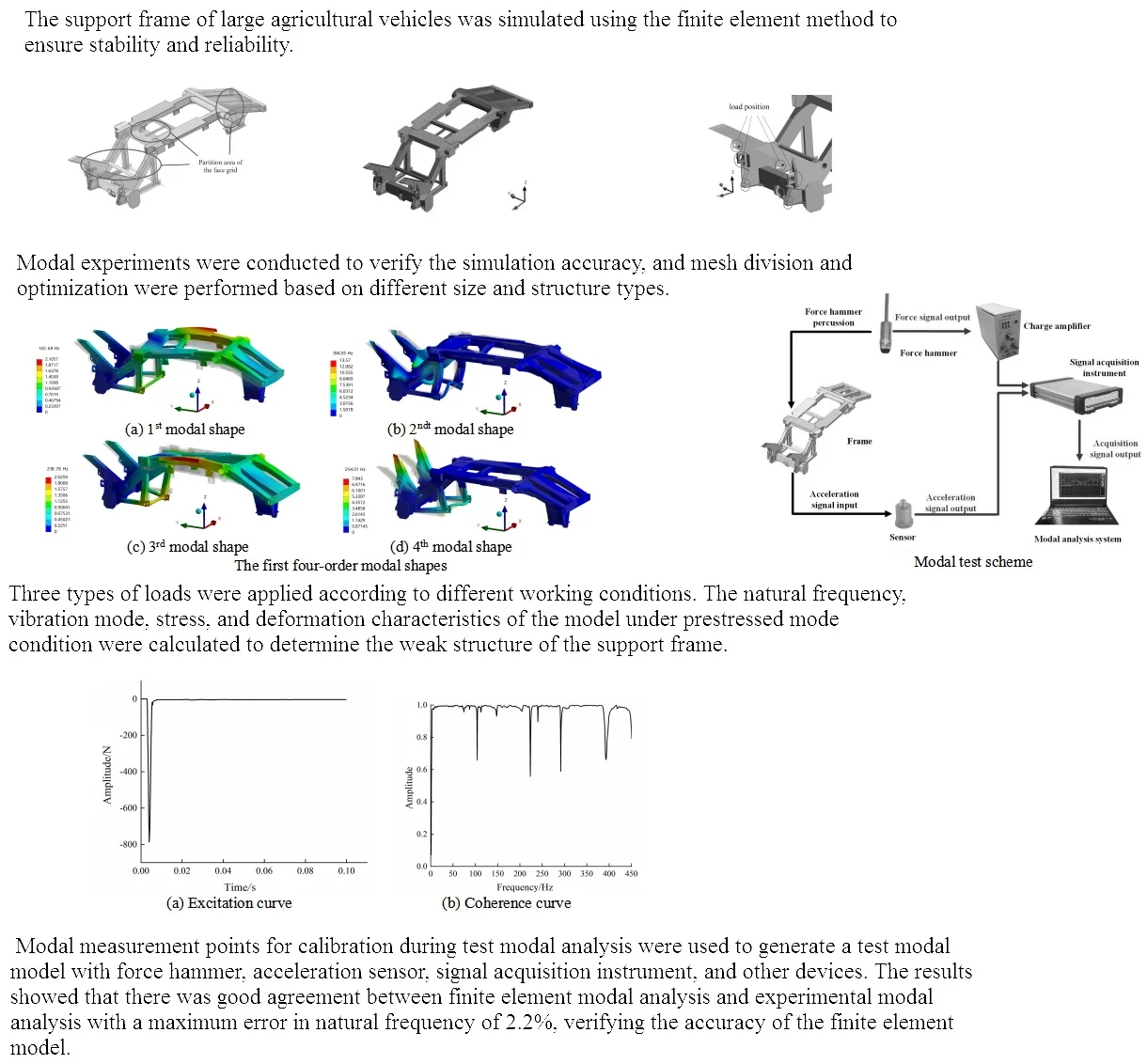
The three-dimensional model of the support frame was imported into the finite element analysis software ANSYS Workbench and subsequently underwent appropriate simplification. Non-essential features such as part chamfers and mounting holes, which had negligible impact on overall model meshing quality, were disregarded. Furthermore, materials were assigned, meshing was refined, and constraints were applied. The support frame comprises several thin-walled components with a thickness ranging from 5-10 mm, which is relatively small in comparison to the overall structure. Directly dividing the grid without processing would lead to an increase in computational workload. Midface extraction can be employed for simplifying the thin-walled parts of the model. To enhance computational efficiency, midface extraction processing of these thin-walled parts is conducted within the Design Modeler module.

Mesh division, as a critical component of model pre-processing, exerts significant influence on the accuracy of subsequent strength and modal analysis results. The support frame exhibits complex structures and non-uniform sizes, rendering the tetrahedron-led method an expedient choice for accelerating the division process and enhancing grid precision. To ascertain the superior quality of the model post midplane extraction compared to its pre-processed state, identical grid divisions are applied to both iterations of the support frames. Typically serving as a benchmark for evaluating mesh quality, grid measurement yields an average unit quality of 0.36, indicating subpar performance. In contrast, the treated model demonstrates an average mesh quality of 0.71, underscoring its enhanced quality relative to its untreated counterpart. The optimized grid division model is shown in Fig. 1.

Fig. 1The optimized grid division model

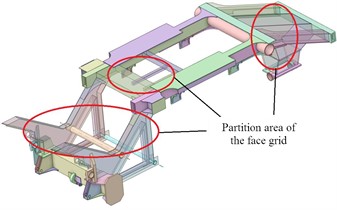
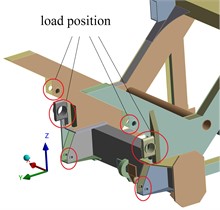
The external load, in addition to its own weight, is distributed as follows: the engine load acts on the rear, the fan load acts on the front, and the picking head and cab loads act on the front. The load is connected to the picking head suspension through three hinge holes on the rack. The forces acting on these three hinge holes are intricate, as depicted in Fig. 2(a). All loads can be applied in the Workbench, and the direction of these loads is shown in Fig. 2(b).

Fig. 2Setting of load

a) Load position of hinge holes

b) Load direction

2.2. Finite element modal analysis

Modal analysis, as a research methodology in the field of structural dynamics, is commonly employed for studying structural vibrations. It encompasses two main approaches: finite element modal analysis and experimental modal analysis. The former involves discretizing the structure, establishing a mathematical model to determine system eigenvalues, and solving for the eigenvalues and eigenvectors of the system – which represent its natural frequencies. ANSYS Workbench is employed for conducting theoretical modal analysis of the frame, which encompasses free and prestressed modes within the software. The free mode represents the unconstrained state of the structure, reflecting its inherent properties. Conversely, the prestressed mode depicts the modal solution under specific boundary conditions and loads, showcasing structural characteristics under constraints. While free modal analysis is easily simulated but costly to conduct experimentally, it becomes challenging due to the large mass and high stiffness of the support frame, making it difficult to achieve free boundary conditions using springs. Therefore, prestressed modal analysis provides a more accurate representation of modal characteristic parameters under operational conditions.

The first four-order modal shapes were depicted in Fig. 3. It is evident from the figure that the first-order natural frequency is 142 Hz, with an overall vibration mode characterized by torsional motion of the welding frame around the $Y$ axis, and bending of both left and right longitudinal beams as well as the back longitudinal beam along the $Z$ axis in unison, with maximum displacement occurring at midspan of the left and right longitudinal beams. The second order natural frequency is 184 Hz, revealing a vibration mode where the entire frame exhibits sinusoidal bending on the $Z$ axis coupled with torsional motion around the $Y$ axis, with maximum amplitude located at a specific position on welded frame. The natural frequency of the third order is 218 Hz, and the mode is wavy bending on the $Z$-axis, while twisting on the $Y$-axis, and the maximum amplitude is located at the stringer position. The fourth order natural frequency is 254 Hz, the mode is a torsional mode on the $Y$-axis, and the maximum amplitude is located at the welding frame position.

Fig. 3The first four-order modal shapes

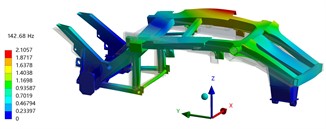
a) 1st modal shape

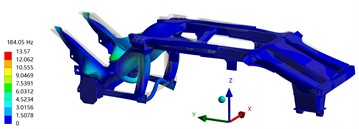
b) 2ndt modal shape

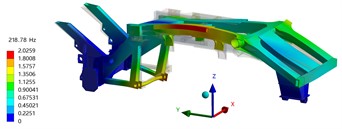
c) 3rd modal shape

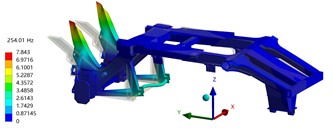
d) 4th modal shape

2.3. Strength analysis

The equivalent stress and total deformation under loading conditions are illustrated in Fig. 4. It is observed that, due to the planar configuration of the mechanism, the maximum equivalent stress occurs at the joint of the rear bridge welding frame following a shift in the center of gravity, with a peak value of 105 MPa. Under standard operating conditions, with a safety factor of 1.5, the allowable stress is 230 MPa. Thus, the maximum stress remains significantly below this threshold at 230 MPa. Consequently, there is no necessity for stress optimization. The total deformation spans from 0 to 0.841 mm, with maximal deformation occurring in the outer connecting plate; minimal distortion takes place within the main body itself. As such, it can be concluded that under transportation conditions, structural strength aligns with design requirements.

Based on the strength analysis, it can be concluded that the support frame possesses adequate strength to meet operational requirements. Subsequent optimization focuses on reducing weight while maintaining optimal stiffness and strength, rather than prioritizing it as the primary objective of the optimization process. The support frame undergoes finite element analysis to assess stress and deformation under unloading conditions, as depicted in Fig. 5. The maximum equivalent stress is concentrated at the joint of the rear axle welded frame, reaching a peak value of 126 MPa. Overall stress levels predominantly remain below 50 MPa, significantly lower than the allowable stress threshold of 230 MPa even without optimization. The total deformation range for the support frame spans from 0 to 0.939 mm, with the outer connecting plate exhibiting maximum deformation while minimal distortion occurs within the main body structure. Consequently, it can be concluded that the structural integrity under unloading conditions satisfactorily aligns with design specifications.

Fig. 4Strength analysis results under loading conditions

a) Stress nephogram

b) Displacement nephogram

Fig. 5Strength analysis results under unloading conditions

a) Stress nephogram

b) Displacement nephogram

3.1. Design of experimental scheme

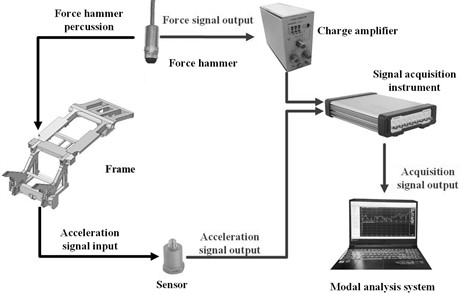
The specific procedure for experimental modal testing is depicted in Fig. 6. Excitation equipment typically involves the use of an exciter and an impact hammer for stimulation. The advantage of the exciter lies in its capacity to deliver substantial excitation energy, as well as its versatility in applying various excitation methods and ease of control. Conversely, the force hammer offers simplicity, making it suitable for field testing without impacting the dynamic characteristics of the specimen. The vibration pickup component comprises a force sensor and an accelerometer sensor, with the latter demonstrating excellent stability and a wide dynamic range. Given the challenges associated with installing and operating a vibration exciter, alongside the convenience and non-intrusive nature of using a force hammer on specimen dynamics, this study opts for utilizing the force hammer as the test vibration excitation equipment while employing an acceleration sensor as the vibration pickup device.

The study primarily focuses on the parameters of low-frequency orders (0-400 Hz). Generally, the single-point excitation method is adequate for inducing modal response. In conjunction with the testing equipment, a combination of single-point excitation and multi-point output method is employed, utilizing a force hammer as the single-point input excitation and an acceleration sensor to capture the output signal. In accordance with Shannon’s sampling theorem, the sampling frequency must be at least twice that of the highest frequency present in the measured signal. Taking into account the impact of low-frequency vibrations generated by large agricultural machinery, an analysis of modal response within 400 Hz is conducted, and an acceleration sampling frequency of 2500 Hz is established. Subsequently, DASP modal analysis software is employed to compute the corresponding pulse signal, response signal, and coherent signal.

Fig. 6Modal test scheme

3.2. Analysis of test results

The results of the signal test are depicted in Fig. 7. It is evident that there is minimal pulse fluctuation from the beginning to the end of the signal, with a brief duration and absence of distortion or overload phenomena, indicating satisfactory quality.

Fig. 7The results of the signal test

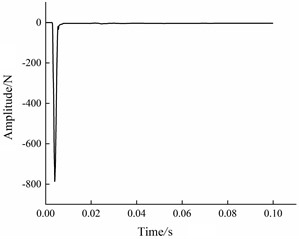
a) Excitation curve

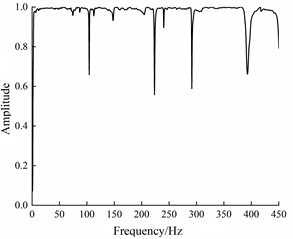
b) Coherence curve

Analysis of the coherence function diagram reveals superior coherence within the frequency range of 0-400 Hz, a significant decrease in coherence at the anti-formant, and near-perfect coherence at other frequencies, signifying high measurement quality. By utilizing modal analysis software to compute the system's response function and correlating the response parameters with the response test model, it is possible to determine the natural frequency and mode shapes. The extraction of second-order frequencies and vibration modes at the front of the rack is illustrated in Fig. 8. As depicted in the figure, significant deformation occurs at the front and side load positions during testing, followed by deformation at the longitudinal beam position, and finally at the rear longitudinal beam position. This pattern closely aligns with results obtained from finite element modal analysis. Consequently, substantial front and side deformation should be considered in subsequent structural improvement processes. By comparing the results of finite element modal analysis and experimental modal analysis, it can be seen that the modal patterns are consistent and the maximum error of natural frequency is less than 2.2 %, which indicates that the finite element model has good accuracy.

Fig. 8The first two-order modal shapes

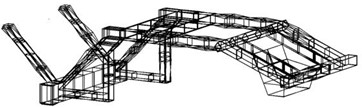
a) 1st modal shape (139.78 Hz)

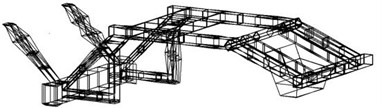
b) 2ndt modal shape (181.54 Hz)