A broadband variable fluid damper with frequency selective valves for spacecraft micro-vibration isolation

Wang, Wenlin; Liu, Yong; Chen, Ruxing; Ding, Yang; Li, Haoyu

doi:10.21595/vp.2024.24190

Vibroengineering Procedia

Browse Procedia

Published: 27 September 2024

Check for updates

A broadband variable fluid damper with frequency selective valves for spacecraft micro-vibration isolation

Wenlin Wang¹

Yong Liu²

Ruxing Chen³

Yang Ding⁴

Haoyu Li⁵

^{1, 3}School of Mechanical Engineering, Dongguan University of Technology, Dongguan, 523808, China

^{2, 4, 5}Beijing Institute of Structure and Environment Engineering, Beijing, 100076, China

Corresponding Author:

Yong Liu

Cite the article Download PDF

Downloads 48

Abstract

In order to improve the vibration isolation performance of current three-parameter damper using bellow and fluid damping, a concept of fluid damper with variable damping and secondary variable stiffness was proposed, a prototype has been designed with several frequency selective valves to adjust the damping characteristics at specific frequency bands, especially that in the low-frequency range. Followed mathematical modelling and simulation of the damper have been carried out, the results show that the designed damper has obtained excellent damping characteristics both in the high- and low-frequency ranges, the micro-vibration isolation efficiency of the damper under realistic excitation of a Control Moment Gyroscope used in a manned spacecraft reaches a significant 71.03 %.The proposed damper concept and designed prototype have laid the foundation for further testing and optimization of high-end isolators for modern spacecrafts.

1. Introduction

Fluid dampers are widely used in spacecrafts for impact and/or vibration mitigation during launching and on orbit [1, 2] or landing [3]. Damper using bellow and fluid damping originated from the two-parameter D-Strut developed by the early American Honeywell company for NASA, subsequently, many studies have been carried out and technical progress has been made. For example, various three-parameter dampers with secondary chambers [4-8] have been proposed. Compared with that of two-parameter dampers, the vibration isolation performance of three-parameter dampers has been significantly improved in the high-frequency range [1, 8], but the vibration isolation performance in the low-frequency range, including the resonance peak area, has not been improved.

A concept of a broadband fluid damper with variable hydraulic damping and secondary variable stiffness was first proposed, and a prototype has been designed with several frequency selective valves (FSVs) to adjust the damping characteristics at specific frequency bands, especially that in the low-frequency range. Mathematical modelling and simulation of the damper have been carried out, and the results show that the fabricated damper has obtained excellent vibration reduction performance both in the high- and low-frequency ranges, the proposed damper concept, designed prototype and research results in this study have laid the foundation for further testing and product optimization for modern spacecraft.

2. Design of a broadband variable fluid damper

As shown in Fig. 1(a), a type of fluid damper with variable damping and secondary variable stiffness was designed, the damper has four chambers filled with silicone oil, i.e., the upper and lower main chambers and the upper and lower secondary chambers. When the piston is actuated by spacecraft vibrations, the silicone oil will be forced through the damping systems embedded in the piston and produce damping forces. Fig. 1(b) illustrates that the damper has five parameters, which has an obvious advantage over the current three-parameter damper by enabling the damping element $C_{A}$ to be variable.

Fig. 2 demonstrates the damping system embedded in the piston assembly. The fluid damping system includes a constant orifice and three FSVs, the three FSVs are arranged in a circular pattern around the constant orifice. The three FSVs are all low-frequency valves and designed to be normally open, but their natural frequencies are different. If the outside excitation frequency coincided with the natural frequency of a FSV, the valve ball of the FSV would resonant and close the valve, so the total damping effect of the damper would be increased, thus, the three FSVs would obviously improve the damping performance of the damper in the low-frequency band.

Fig. 1Prototype design and mechanical model of a broadband variable fluid damper

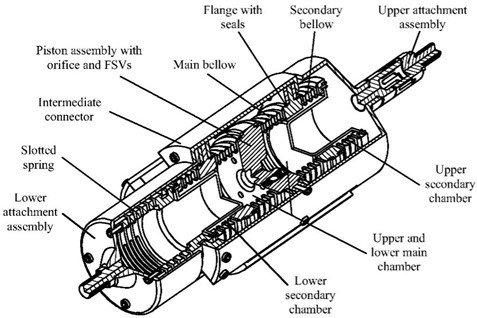
a) A broadband variable fluid damper

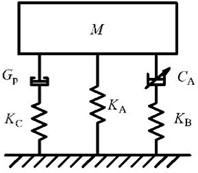
b) Mechanical model of the damper

Fig. 2The damping system with constant orifice and FSVs in the piston assembly

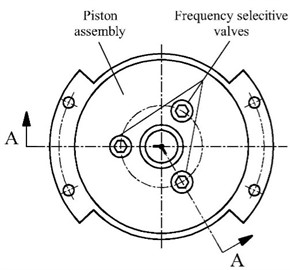
a) Top view of the piston assembly

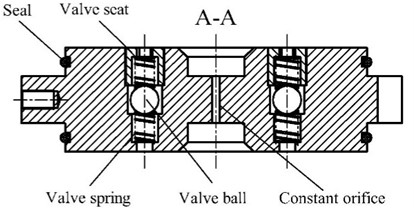
b) A-A cross-section

3. Modelling the characteristics of the damper

Fig. 3 demonstrates the physical principle or model of a broadband variable fluid damper designed in the last section for micro-vibration reduction of a Control Moment Gyroscope (CMG) used in a manned spacecraft.

The stiffness of the two main bellows is given by:

1

K_{A} = M_{C} (2 π f_{n 1})^{2},

where $M_{C}$ is the CMG mass and $f_{n 1}$ is the first-order natural frequency of the isolation system.

Fig. 3Physical model of a broadband variable fluid damper used for micro-vibration reduction of a Control Moment Gyroscope (CMG) used in a manned spacecraft

Physical model of a broadband variable fluid damper used for micro-vibration reduction of a Control Moment Gyroscope (CMG) used in a manned spacecraft

The minimum vibration transmissibility [6] of a isolation system with basic three-parameter damper can be expressed as:

2

T_{m i n} = \sqrt{\frac{N + 2}{{(1 - \frac{2 (N + 1)}{N + 2})}^{2} + \frac{1}{N + 1} {(N + 1 - \frac{2 (N + 1)}{N + 2})}^{2}}} = \frac{N + 2}{N},

where $N$ is the stiffness ratio of secondary bellow to main bellow, i.e., $N = K_{B} / K_{A}$ , the recommendation value of $N$ is 1-2. In addition, stiffness of the slotted spring [9, 10] in the damper can be expressed by:

3

K_{C} = \frac{4 E a h^{3}}{n R^{3}} / [\frac{3}{2} π - \frac{12}{π} + \frac{1 + ν}{γ} (\frac{3}{2} π - \frac{2}{π} - 4)],

where $E$ , $ν$ are respectively the elastic modulus and the Poisson’s ratio of the spring material, the others are all geometric parameters of the spring.

Under micro vibrations of the CMG, the dynamics of the isolation system with the fluid damper can be expressed as:

4

M_{C} {\ddot{x}}_{1} + A_{e} s g n ({\dot{x}}_{1}) (p_{1} - p_{2}) + K_{A} x_{1} = \{\begin{array}{l} F_{C} (t) - K_{C} [x_{1} - s g n (x_{1}) G_{p}], |x_{1}| > G_{p}, \\ F_{C} (t), |x_{1}| \leq G_{p}, \end{array}

where $x_{1}$ is the displacement of the CMG, $A_{e}$ is the equivalent area of the bellow which is actuated by fluid, $p_{1}$ and $p_{2}$ are the pressures of the upper and lower main chambers, $F_{C} (t)$ is the disturbance force function of the CMG, G_P is the gap for the slotted spring to function.

In addition, by referring to Fig. 3, the fluid continuity equation in the damper under vibrations can be formulated by:

5

A_{e} s g n ({\dot{x}}_{1}) {\dot{x}}_{1} = q_{1} + q_{2} + q_{3},

where $q_{1}$ , $q_{2}$ and $q_{3}$ are respectively the flow rates passing through the constant orifice, passing through the FSV system and forced into the upper or lower secondary chambers, $q_{1}$ , $q_{2}$ and $q_{3}$ can be formulated by:

6

\{\begin{array}{l} q_{1} = C_{d 1} (\frac{π}{4} {d_{1}}^{2}) \sqrt{\frac{2}{ρ} s g n ({\dot{x}}_{1}) (p_{1} - p_{2})}, q_{2} = \sum_{i = 1}^{3} C_{d 2} A_{x i} \sqrt{\frac{2}{ρ} s g n ({\dot{x}}_{1}) (p_{1} - p_{2})}, \\ q_{3} = \frac{π d_{3} δ^{3}}{12 μ L} (p_{1} － p_{3 u}), s g n ({\dot{x}}_{1}) = 1, q_{3} = \frac{π d_{3} δ^{3}}{12 μ L} (p_{2} － p_{3 d}), s g n ({\dot{x}}_{1}) = - 1, \end{array}

where $C_{d 1}$ and $C_{d 2}$ are the discharge coefficients of the constant orifice and the FSVs, $A_{x i}$ ( $i =$ 1~3) are flow areas of the FSVs, $p_{3 u}$ and $p_{3 d}$ are the pressures of the upper and lower secondary chambers, $μ$ is the dynamic viscosity of the silicone oil, the others are geometric parameters of the annular passage between the main chamber and the secondary chamber.

4. Simulation and analysis

With the mathematical model developed, MATLAB/Simulink models for the fluid damper and the above vibration isolation system have been established for simulation. In the simulation process, some of the main parameters and values include $M_{c} =$ 34 kg, $K_{A} = K_{B} = K_{C} =$ 1.3745×10⁶ N/m, $A_{e} =$ 7.49×10^-4 m², $d_{1} =$ 2.5×10^-3 m, $C_{d 1} =$ 0.80, $C_{d 2} =$ 0.60, natural frequencies of the three FSVs are respectively 25 Hz, 32 Hz and 40 Hz, and some of the results obtained are shown by Figs. 4-6.

Fig. 4Response characteristics of the fluid damper (simulation condition: sinusoidal chirp excitation with displacement amplitude ±0.1 mm, frequency range 0.1-500 Hz in 3 seconds)

Response characteristics of the fluid damper (simulation condition: sinusoidal chirp excitation with displacement amplitude ±0.1 mm, frequency range 0.1-500 Hz in 3 seconds)

a) Ball displacements of the FSVs

b) Damping force profile of the fluid damper

Figs. 4(a) and (b) obviously demonstrate the response nature of the FSVs and the damper under sinusoidal chirp excitation condition. The three FSVs will close when the excitation frequencies coincide with their natural frequencies and thus improve damping force of the damper at these frequencies, because the three FSVs are all designed in the low-frequency range, so Fig. 4(b) shows that the damping forces in low-frequency range are obviously larger, and that in the middle to high frequency range are obviously smaller, in other words, the fluid damper has obtained larger damping coefficient at the low-frequency range and smaller coefficient at the middle- to high-frequency range, thus, the fluid damper has obtained excellent damping characteristics in a broadband.

Fig. 5 shows the damping characteristics of the fluid damper when subject to a sinusoidal excitation of displacement amplitude ±0.1 mm and frequency 32 Hz which coincides with the natural frequency of the No. 2 FSV. Fig. 5(a) and 5(b) demonstrate that the fluid damper has obtained stable and idea damping characteristics.

Fig. 5Damping characteristics of the fluid damper (simulation condition: sinusoidal excitation with displacement amplitude ±0.1 mm and frequency 32 Hz)

Damping characteristics of the fluid damper (simulation condition: sinusoidal excitation with displacement amplitude ±0.1 mm and frequency 32 Hz)

a) Force-displacement characteristics

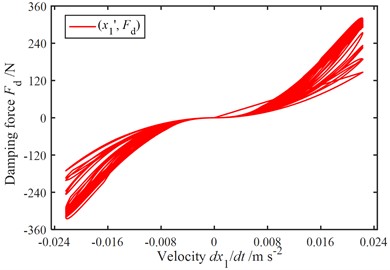
b) Force-velocity characteristics

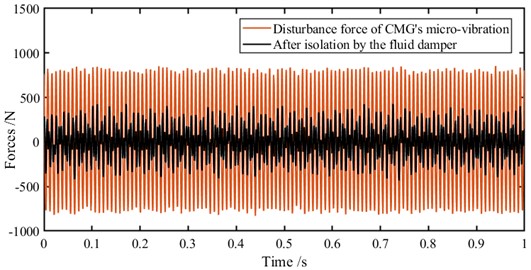
Fig. 6 shows the micro-vibration isolation performance of the fluid damper under realistic excitation of a CMG [11, 12] used in a manned spacecraft. It demonstrated that the micro-vibration of the CMG has been obviously mitigated, the Root Mean Square (RMS) value of CMG disturbance force 548.1 N has been reduced to 158.8 N after isolation, thus the vibration efficiency of the isolation system with the broadband variable fluid damper reaches a significant 71.03 %.

Fig. 6Micro-vibration isolation performance of the fluid damper (simulation condition: experimental disturbance force profile of a CMG’s macro-vibration)

5. Conclusions

1) A concept of a broadband fluid damper with variable hydraulic damping and secondary variable stiffness was proposed, and a prototype has been designed with several frequency selective valves to adjust the damping characteristics at specific frequency bands, especially that in the low-frequency range.

2) Mathematical modelling and simulation of the damper have been carried out, the results show that the designed damper has obtained excellent damping characteristics both in the high- and low-frequency ranges, the micro-vibration isolation efficiency of the fluid damper under realistic excitation of a CMG used in a manned spacecraft reaches a significant 71.03 %.

3) The damper concept and designed prototype have laid the foundation for further testing and optimization of high-end isolators for modern spacecrafts.

References

Liu Xing-Tian, Kong Xiang-Sen, Shen Jun-Feng, and Zhou Xu-Bin, “Vibration isolator with relaxation type damping for micro-vibration isolation from satellite remote sensors,” (in Chinese), Optics and Precision Engineering, Vol. 25, No. 9, pp. 2448–2453, Jan. 2017, https://doi.org/10.3788/ope.20172509.2448

Publisher
L. Li, L. Yuan, L. Wang, R. Zhen, X. Y. Wang, and Y. P. Wu, “Influence of micro vibration on measurement and pointing control system of high-performance spacecraft from Hubble Space telescope,” (in Chinese), Optics and Precision Engineering, Vol. 28, No. 11, pp. 2478–2487, 2020, https://doi.org/10.3788/ope.20202811.2478

Publisher
S. Yue, B. Titurus, Z. Li, C. Wu, and Z. Du, “Analysis of liquid spring damper for vertical landing reusable launch vehicle with network-based methodology,” Nonlinear Dynamics, Vol. 111, No. 3, pp. 2135–2160, Oct. 2022, https://doi.org/10.1007/s11071-022-07944-z

Publisher
B. Paul, R. Reg, and B. Suat, “Hydraulic damper,” European Patent, EP3521654, 2021.

Search CrossRef
X. L. Jiao, Y. Zhao, W. L. Ma, and S. L. Li, “Normalized model of a three-parameter isolation system and its parametric optimization,” (in Chinese), Journal of Vibration and Shock, Vol. 37, No. 21, pp. 204–212, 2018, https://doi.org/10.13465/j.cnki.jvs.2018.21.029

Publisher
C. Wang, “Design and experiment of a three-parameter isolation system with optimal damping,” (in Chinese), Journal of Mechanical Engineering, Vol. 51, No. 15, p. 90, Jan. 2015, https://doi.org/10.3901/jme.2015.15.090

Publisher
W.-K. Shi, C. Qian, Z.-Y. Chen, Y. Cao, and H.-H. Zhang, “Modeling and dynamic properties of a four-parameter zener model vibration isolator,” Shock and Vibration, Vol. 2016, pp. 1–16, Jan. 2016, https://doi.org/10.1155/2016/5081812

Publisher
X. Jiao, Y. Zhao, and W. Ma, “Nonlinear dynamic characteristics of a micro-vibration fluid viscous damper,” Nonlinear Dynamics, Vol. 92, No. 3, pp. 1167–1184, Feb. 2018, https://doi.org/10.1007/s11071-018-4116-2

Publisher
C. Liu and K. Yu, “Design and experimental study of a quasi-zero-stiffness vibration isolator incorporating transverse groove springs,” Archives of Civil and Mechanical Engineering, Vol. 20, No. 3, pp. 1–21, Jun. 2020, https://doi.org/10.1007/s43452-020-00069-3

Publisher
V. Balambica and V. Deepak, “Static analysis of slotted springs,” in International Conference on Automatic Control and Dynamic Optimization Techniques (ICACDOT), pp. 455–459, Sep. 2016, https://doi.org/10.1109/icacdot.2016.7877627

Publisher
L. Minghui, C. Hui, L. Chuang, H. Xiaojian, W. Dong, and Y. Jiang, “Micro-vibration test of high resolution spacecraft,” Journal of Physics: Conference Series, Vol. 1877, No. 1, p. 012021, Apr. 2021, https://doi.org/10.1088/1742-6596/1877/1/012021

Publisher
J. You, L. K. Yao, H. Wang, Y. Q. Hou, and W. W. Jin, “Analysis and validation of vibration and noise control of control moment gyroscope on a sealed capsule,” (in Chinese), Noise and Vibration Control, Vol. 42, No. 2, pp. 85–89, 2022.

Search CrossRef

About this article

Received

13 May 2024

Accepted

07 June 2024

Published

27 September 2024

SUBJECTS

Vibration control, generation and harvesting

DOI

https://doi.org/10.21595/vp.2024.24190

Keywords

variable fluid damper

frequency selective valve

broadband

damping characteristics

micro-vibration isolation

spacecraft

Acknowledgements

The authors thank funding support from the National Natural Science Foundation of China (NSFC) under Grant No. 12072075.

Data Availability

The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

Conflict of interest

The authors declare that they have no conflict of interest.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2021 12 02

Effect of mounting and fluid parameters on dynamic damping characteristics of a hydraulic damper

Wenlin Wang, Rongyong Li, Shan Zhu, Yongming Wu

Research article

2017 12 31

Active vibration isolation using a six-axis orthogonal vibration isolation platform with piezoelectric actuators

Shuai Wang, Zhaobo Chen, Yinghou Jiao, Xiaoxiang Liu

Review article

2017 08 15

Invited Review: Recent developments in vibration control of building and bridge structures

Khaled Ghaedi, Zainah Ibrahim, Hojjat Adeli, Ahad Javanmardi

Research article

2017 06 30

Hybrid model predictive control of damping multi-mode switching damper for vehicle suspensions

Xiaoqiang Sun, Yingfeng Cai, Chaochun Yuan, Long Chen, Ruochen Wang

W. Wang, Y. Liu, R. Chen, Y. Ding, and H. Li, “A broadband variable fluid damper with frequency selective valves for spacecraft micro-vibration isolation,” Vibroengineering Procedia, Vol. 55, pp. 67–72, Sep. 2024, https://doi.org/10.21595/vp.2024.24190

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/vp.2024.24190
UR  - https://doi.org/10.21595/vp.2024.24190
TI  - A broadband variable fluid damper with frequency selective valves for spacecraft micro-vibration isolation
T2  - Vibroengineering Procedia
AU  - Wang, Wenlin
AU  - Liu, Yong
AU  - Chen, Ruxing
AU  - Ding, Yang
AU  - Li, Haoyu
PY  - 2024
DA  - 2024/09/27
PB  - Extrica
SP  - 67-72
VL  - 55
SN  - 2345-0533
SN  - 2538-8479
ER  - 

Copy Ris

Copied to clipboard!

 @article{Wang_2024, title={A broadband variable fluid damper with frequency selective valves for spacecraft micro-vibration isolation}, volume={55}, ISSN={2538-8479}, url={https://doi.org/10.21595/vp.2024.24190}, DOI={10.21595/vp.2024.24190}, journal={Vibroengineering Procedia}, publisher={JVE International Ltd.}, author={Wang, Wenlin and Liu, Yong and Chen, Ruxing and Ding, Yang and Li, Haoyu}, year={2024}, month=sep, pages={67–72} }

Copy Bibtex

Copied to clipboard!

[1]W. Wang, Y. Liu, R. Chen, Y. Ding, and H. Li, “A broadband variable fluid damper with frequency selective valves for spacecraft micro-vibration isolation,” Vibroengineering Procedia, vol. 55, pp. 67–72, Sep. 2024, doi: 10.21595/vp.2024.24190.

Copy IEEE

Copied to clipboard!

Wang, Wenlin, Yong Liu, Ruxing Chen, Yang Ding, and Haoyu Li. “A Broadband Variable Fluid Damper with Frequency Selective Valves for Spacecraft Micro-Vibration Isolation.” Vibroengineering Procedia 55 (September 27, 2024): 67–72. https://doi.org/10.21595/vp.2024.24190.

Copy Chicago

Copied to clipboard!

A broadband variable fluid damper with frequency selective valves for spacecraft micro-vibration isolation

Abstract

1. Introduction

2. Design of a broadband variable fluid damper

3. Modelling the characteristics of the damper

4. Simulation and analysis

5. Conclusions

References

About this article

Related Articles