Efficient identification of geometric errors in CNC machine tools based on dual-frequency laser interferometry

3.1. Bias-preserving fiber-coupled dual-frequency laser interferometric elongation measurement by CNCM

CNCM is a kind of equipment that uses digital information to control the machine tool so as to realize automatic machining. It's widely utilized in the manufacturing of machinery, aircraft, automobiles, and other industries because of its high precision, high efficiency, and high reliability. CNCM is mainly composed of three main parts: computer control system, servo drive system and machine body. It receives the input machining program, processes it, and outputs control instructions to direct the various parts of the machine tool to carry out the specified actions. The computer control system is the central component of CNCM. The servo drive system serves as the actuator of CNCM, driving the machine’s various parts according to the control instructions. The machine body is the basic part of the CNCM, which includes the bed, spindle, table and other components, and is the main body to realize machining [22]. The details are shown in Fig. 1.

Fig. 1CNC machine tool structure diagram

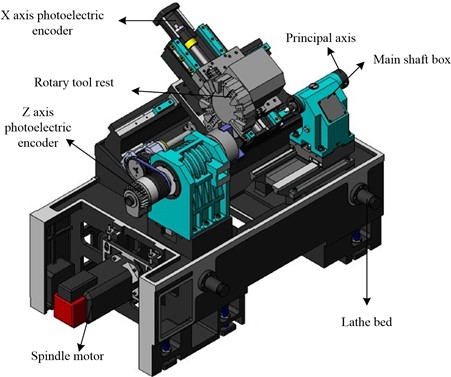
The geometrical parameters and locations of different machine tool components or parts that deviate from the ideal geometrical parameters and positions due to flaws in machine tool assembly, manufacture, design, and other processes are referred to as the GE of CNCM. The GE of CNCM can be measured and analyzed by the bias-preserving fiber (BPF)-coupled DFLs interferometric length measurement of CNCM. The principle of BPF-coupled DFLs interferometric elongation of CNCM is mainly based on laser interferometry. In particular, a monochromatic, coherent, narrow laser beam is produced by a laser and split into two beams, which are referred to as the measurement light and the reference light. A mirror reflects the reference light, which then collides with the measurement light. The measuring light strikes the object to be measured, is reflected and meets the reference light again. Where they meet, the reference light and the measuring light form interference fringes. This is due to the interference phenomenon that occurs when two light waves are coherently superimposed. Since the amount of interference fringes closely correlates with the object's length, counting interference fringes can be used to determine an object's length. The purpose of BPF is to maintain the stability of the interference fringe by guaranteeing that the light's polarization direction (PD) remains unaltered. Through BPF coupling, the influence of environmental factors on the interference fringes can be effectively suppressed, and the accuracy and stability of the measurement can be improved. The system structure of the BPF-coupled DFLI to measure the position error of the linear guideway mainly consists of the following parts, laser, beam splitter, interferometer, and controller. Furthermore, the discrepancy between the theoretical and actual interference fringes can be used to calculate the location error of the linear guide. This system structure can measure the position error of the linear guide with high precision and high efficiency, and provide powerful technical support for the fields of machinery manufacturing and aerospace. Specifically shown in Fig. 2.

Fig. 2Dual-frequency laser interferometer system structure

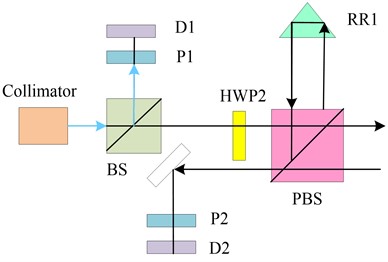
In the ideal case, two orthogonal beams of linearly polarized light with frequencies $f_1$ and $f_2$ emitted by a He-Ne DFLs are shown in Eq. (1):

where, ${\overrightarrow{E}}_1$ and ${\overrightarrow{E}}_2$ are the amplitudes of the two beams of light, $f_1$ and $f_2$ are their respective frequencies, and ${\varphi }_{01}$ and ${\varphi }_{02}$ are their respective initial phases. Because of their differing frequencies, these two light beams cause interference phenomena when they travel through space. The phase difference between the two light beams accounts for the variations in brightness and dark in the interference fringes. The interference fringes are bright when the phase difference between the two light beams is an integer multiple of $2\pi$. The interference fringes are in a dim or disappearing state when the phase difference is a non-integer multiple of $2\pi$. The phase difference between the two laser beams can be ascertained by measuring the changes in the interference fringes, which provides details about the object being tested. It is coupled into the optical fiber through a coupling mirror, and in the middle, the vibration direction of the line polarization is adjusted by a half-wave plate HWP1 to align the two beams of orthogonally polarized light to the main axis of the optical fiber. The orthogonally polarized light is transmitted along the BPF after incidence, and the output beam at the other end of the fiber enters the measurement unit through a collimating beam expander. In the measurement cell, an interferometer can be used to measure the interference fringes of the two orthogonally polarized beams. The usual components of an interferometer are a detector, a mirror, and a beam splitter. The entering beam is divided into two beams by the beam splitter: a reference beam and a measuring beam. The reference light is reflected by the reflector back to the beam splitter, where it re-emerges with the measurement light. At the point of encounter, the two beams interfere, forming an interference fringe. The detector detects the changes in the interference fringes and thus obtains information about the object to be measured. The two orthogonally polarized beams' vibration direction can be altered, which will alter the interference fringes' position and shape, by varying the half-wave plate HWP1's angle. The position error of the observed object can be calculated by comparing the difference between the theoretical and real interference fringes [23-24]. The reference light beat frequency is shown in Fig. 3.

Fig. 3Reference light beat frequency

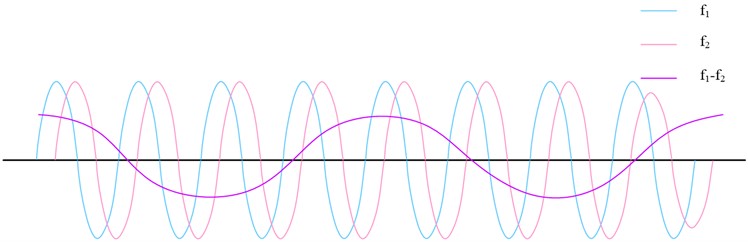
There are two main ways to process outlier signals, displacement demodulation and phase demodulation. By comparing and computing the Doppler frequency difference between the reference signal and the measurement signal, displacement demodulation uses the technique of frequency difference integration to ascertain an object's displacement. The reference signal is shown in Eq. (2):

where, $S_r$ denotes the reference signal. The measurement signal is shown in Eq. (3):

where, $S_m$ denotes the measurement signal. The relationship between frequency difference and displacement is shown in Eq. (4):

The measurement of the phase difference between the signal and the reference signal allows for the realization of phase demodulation, a measurement approach based on phase difference. The reference signal is shown in Eq. (5):

where, $S_r$ denotes the reference signal. The measurement signal is shown in Eq. (6):

where, $S_m$ denotes the measurement signal. The relationship between frequency difference and displacement is shown in Eq. (7):

3.2. DFLI system construction and optimization

The length measurement system of fiber optic coupled DFLI is a kind of displacement measurement system using the principle of optical interference, which adopts DFLI as the core measurement equipment, and transmits the laser beam to the interferometer through the fiber optic coupling technology to achieve high-precision displacement measurement. In the length measurement system of fiber optic coupling DFLI, optical fiber as a transmission medium can effectively avoid the interference of ambient light and improve the stability of the measurement system. At the same time, the laser beam can be conveniently transmitted to the interferometer through the optical fiber transmission to achieve long-distance measurement. BPF is a type of special optical fiber that can be used to provide high-precision physical quantity measurement by maintaining the line PD and increasing the coherent signal-to-noise ratio. A decrease in the polarization preservation performance will result from the structural defects created inside the fiber during the drawing process of BPF. This means that when line-polarized light is transmitted along one of the fiber’s characteristic axes, some of the optical signal will be coupled into the other characteristic axis that is perpendicular to it, which will ultimately lead to a decrease in the polarization extinction ratio of the outgoing polarized light signal. The fiber’s internal birefringence effect is impacted by this flaw. In BPF, a shorter beat length and better maintenance of the transmitted light's polarization state correspond with a stronger birefringence effect [25-26]. The BPF type is shown in Fig. 4.

Fig. 4Polarization-maintaining fiber type

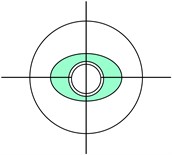
a) Elliptic type

b) Panda type

c) Bow tie type

d) Photonic crystal fiber

Return loss is the number of decibels of the ratio of backward reflected light relative to the input light at the fiber optic connection, which reflects the reflections from the fiber optic link due to impedance mismatches, a pair of wires themselves. The return loss is shown in Eq. (8):

where, $P_{in}$ denotes the incident power and $P_{re}$ denotes the end-plane reflected power. Ideally, the orthogonal dual-frequency line-polarized light emitted from a DFLs should be two perfectly orthogonal line-polarized beams. However, in practice, due to the non-ideal nature of the laser, it is possible that the PDs of the two beams of line polarized light emitted are not perfectly orthogonal, or the line polarized light undergoes elliptical polarization and is no longer perfectly line polarized. The difference between orthogonality error and polarization leakage error is shown in Fig. 5.

Fig. 5The difference between orthogonal error and polarization leakage error

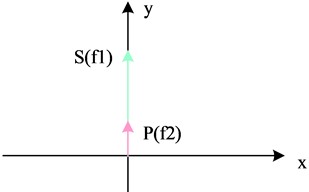
a) Orthogonal error

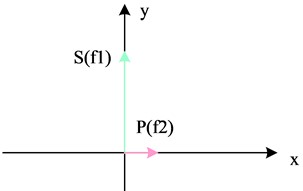
b) Polarization leakage error

The beamsplitter film or glass of a non-polarized beamsplitter may produce the phenomenon of birefringence, and when the direction of birefringence does not coincide with the direction of laser polarization, it will make the linearly polarized light passing through it turn into elliptically polarized light, which will produce frequency aliasing and result in a nonlinear error. The frequency aliasing brought on by the birefringence phenomena is the primary cause of this nonlinear mistake. In a beamsplitter, if a birefringent phenomenon exists in the beamsplitter film or glass, i.e., its refractive index differs for light of different PDs, then when linearly polarized light passes through the beamsplitter, its PD may change, resulting in frequency aliasing. Nonlinear errors are introduced by frequency aliasing, which alters the location and form of the interference fringes. Table 1 lists the primary sources of nonlinear errors.

It can be assumed that all other factors (such as the light source, beam splitter, interferometer, etc.) are ideal when examining the relationship between the nonlinear error in the length measurement results and the fiber alignment error. This means that these factors do not affect the state of polarization of the light and do not introduce additional error. Two linearly polarized lights are assumed to be ideally orthogonal, i.e., $\alpha =\beta$. This means that the PDs of the reference and measurement signals are exactly perpendicular and have no deviation. The expressions for the reference and measurement signals are further simplified based on the above assumptions. Due to $\alpha =\beta$, both signals are polarized in the same direction with only a slight difference in frequency. Therefore, the reference signal is expressed as shown in Eq. (9):

The measurement signal is represented as shown in Eq. (10):

where, ${\omega }_D$ represents the Doppler shift produced by the moving mirror. The effect of temperature on fiber properties does include material thermal expansion and thermo-optic coefficient. When the temperature changes, the fiber material experiences thermal expansion or contraction due to the fact that most materials have the property of thermal expansion and contraction. When the temperature increases, the fiber material expands, resulting in an increase in the length of the fiber. On the other hand, the fiber’s length falls as a result of the fiber optic material contracting when the temperature drops. This thermal expansion of the material results in a change in the geometry and dimensions of the fiber, which affects its transmission performance and optical properties. The length change due to thermal expansion is shown in Eq. (11):

where, $\alpha$ denotes the coefficient of thermal expansion and $L$ denotes the fiber length. The effective refractive index change due to thermo-optic effect is shown in Eq. (12):

where, $\xi \approx$7×10^-6. The total phase change due to temperature change is shown in Eq. (13):

When the temperature changes, the beat length of the BPF changes. This is because temperature changes cause thermal expansion and thermo-optic effects in the fiber material. Therefore, temperature changes can introduce a nonlinear error of period $2\pi$ to the measurements.

4.1. Stability analysis of DFLI

To evaluate the stability of the optical performance of the BPF after multiple plugging and unplugging, the experiment used fixed DFLs and a fixed fiber connector, as well as a spot analyzer to build the optical path. The optical fiber was plugged and unplugged several times on the fixed connector, and after adjusting the collimation, the spot was detected and the coordinates of the spot center were recorded by the spot analyzer two meters away from the fiber connector, as shown in Fig. 6.

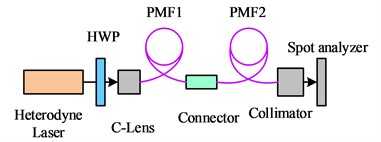
In comparison to the vertical direction, the offset of the spot in Fig. 6 is more noticeable in the horizontal direction. At a distance of 2 m, the offset reaches a maximum of 1 mm, which corresponds to an angular change of up to 1.8 seconds. When performing laser inspection, the power of the laser is usually chosen to be low. This is because the optical power decreases after going through a number of optical elements, which has an impact on the photodetector's ability to detect the spot and further reduces measurement accuracy. To analyze the performance of the BPF more intuitively, the study used an optical power meter to measure the optical power of the light exiting the DFLs, the exiting optical power between the two BPFs, and the final exiting optical power of the BPFs, respectively. This setup is to understand more precisely the power attenuation of the BPF during the transmission process. During the experiment, several plugging and unplugging operations were performed on the BPFs, and the outgoing optical power at three different positions was recorded, as shown in Fig. 7.

Fig. 6Directional stability of the outgoing light of polarization-maintaining fiber

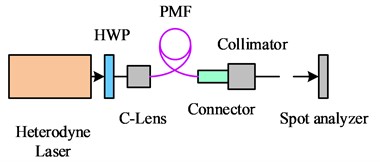
a) Experimental photogram

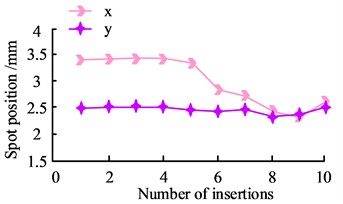
b) Insertion and removal times and spot center position

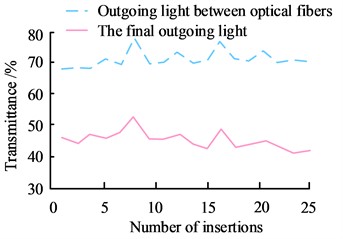
Fig. 7The power of the outgoing light at different positions

a) Experimental photogram

b) Insertion and removal times and spot center position

Fig. 8Dual-frequency laser stability

a) Experimental photogram

b) Dual-frequency laser power change

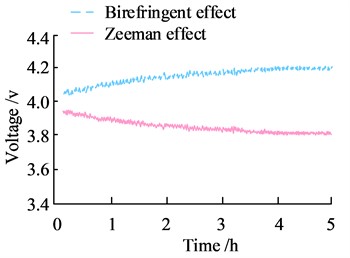
In Fig. 7, the transmittance of the single fiber to the outgoing light from the DFLs is 66 % on average, while the transmittance of the dual fiber to the outgoing light from the DFLs is 44 % on average. Since the two BPFs used in the experiment have the same parameters, it can be inferred that the main reason for the attenuation of the outgoing optical power of the first BPF being larger than that of the second one is the loss when the laser is coupled to the fiber. In order to investigate the power stability of DFLss, as illustrated in Fig. 8, the power stability and polarization stability of two different types of DFLss coupled with BPFs are examined through experiment design and optical path construction.

In Fig. 8, the variation range of the optical power of the Seeman effect-based DFLs over a four-hour period is 2.9 %, while the variation range of the birefringent principle-based DFLs is 3.2 %. This indicates that the power stability of the Seeman effect DFLs is slightly better than that of the birefringent DFLs. The total power ratio of the output of the Seeman effect DFLs to the birefringent DFLs is 3.5:4. This indicates that the total power magnitude of the birefringent DFLs is higher.

4.2. Laser polarization and DFLI performance analysis

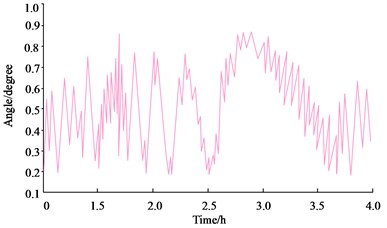
To assess the polarization stability of the light source, the study took the optical power of detectors D2 and D3 for three consecutive hours after the optical path was stabilized. The variation of the vibration angle of the polarization state was obtained by calculation. The comparison between the conventional He-Ne DFLs based on the Seeman effect and the DFLs based on the birefringence effect in terms of polarization angle variation is shown in Fig. 9.

In Fig. 9, the polarization angle variation of the DFLs based on the Seeman effect is in the range of ±0.35°, while that of the DFLs based on the birefringence principle is in the range of ±0.28°. The smaller the polarization angle oscillation, the smaller the frequency mixing phenomenon, thus improving the accuracy of the measurement. In real-world applications, the impact of an external force on the BPF must be taken into account to guarantee measurement accuracy. And the influence of the pressure change and the change in the direction of the force on the BPF birefringence is shown in Fig. 10.

Fig. 9Polarization angle change of dual frequency laser

a) Zeeman effect

b) Birefringent effect

Fig. 10Influence of pressure and force direction on birefringence of polarization-maintaining fiber

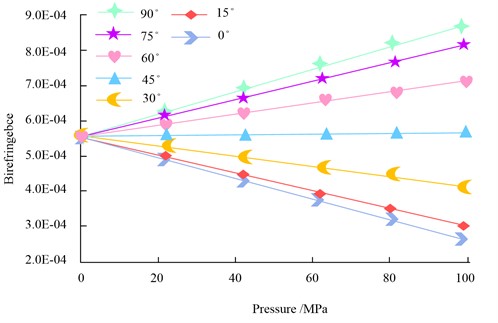
In Fig. 10, different force directions and slow-axis angles lead to different degrees of birefringence effect, and this change affects the transmission characteristics of light in the BPF, which in turn affects the accuracy of the measurement results. In order to verify the effectiveness of the geometric error identification method for CNC machine tools based on dual-frequency laser interferometer, and compare with existing methods, a high-precision dual-frequency laser interferometer is used as the main measurement tool, equipped with necessary optical and mechanical accessories, including mirrors, beam splitters, photodetectors, polarization-maintaining fibers, etc. Select a representative CNC machine tool as the experimental object to ensure that the machine tool type covers the applicable scope of the study. The experiments were conducted in a controlled environment to reduce the impact of environmental factors such as temperature, humidity and vibration on the measurement results. The measurement process is described in detail, including the emission of the laser beam, transmission through the working area of the CNC machine, reflection, and the capture of interference fringes. The experimental Settings of other geometric error identification methods, including reflector method, infrared camera method, frequency domain analysis method, theoretical model method, trajectory method, closed-loop measurement method and linear regression method, were compared in the experiment. Additionally, as Table 2 illustrates, the comparison indices are normalized.

In Table 2, the measurement accuracy, measurement range, ease of operation, reliability, cost, and applicability of the DFLI-based GE identification method for CNCM are 0.91, 0.87, 0.93, 0.77, 0.94, 0.85, and 0.97, respectively, which is a better overall performance than several other methods. At last, the statistical indexes of uncertainty, sensitivity and confidence interval are verified by experiments. Measurement uncertainty refers to the measurement that is different from the real value due to various factors in the measurement process. Sensitivity refers to the ability of a measurement system to respond to small changes in the physical quantity being measured. A confidence interval is the probability that the measured value falls within a certain interval at a certain confidence level. The experiment uses a high-precision dual-frequency laser interferometer as the main measurement tool, equipped with the necessary optical and mechanical accessories, such as mirrors, beam splitters, photodetectors, etc. The experiments were conducted in a controlled environment to reduce the impact of environmental factors such as temperature, humidity and vibration on the measurement results. Firstly, the dual-frequency laser interferometer is calibrated to ensure its measurement accuracy. Then, through a series of standardized tests, data on the geometric errors of CNC machine tools are collected. During this process, measurements are recorded and uncertainty, sensitivity, and confidence intervals are calculated. Statistical software is used to analyze the collected data and calculate the measurement uncertainty and sensitivity. Determine 95 % confidence intervals for measurement accuracy and measurement range based on measurement data. Through accurate experimental design and data analysis, the final results are shown in Table 3.

In Table 3, the measurement uncertainty is ±0.5 microns, which reflects the maximum possible deviation between the measured value and the true value at the 95 % confidence level, indicating that the measurement method proposed in this study has high accuracy and reliability. The sensitivity analysis revealed that the system has a 0.01-micron response to an input change of 1 millivolt, which further demonstrates the high responsiveness of the measurement system and its ability to accurately capture small size changes. In addition, 95 % confidence intervals for measurement accuracy and range were 0.88 to 0.94 and 0.83 to 0.90, respectively, indicating that the measurements were statistically robust.