Dynamic characteristics analysis for gear transmission system in shearer cutting section under different loads

1. Introduction

Gear transmission system is one of the important components of the shearer cutting section, and its performance directly determines the operating efficiency of the shearer cutting section. When the cutting part of the shearer encounters uneven coal seam, gangue and coal rock mass, it will be subjected to a strong impact and large fluctuation load, which will be further transmitted to the gear transmission system, resulting in vibration and noise. When the vibration frequency of the system is not much different from the operating frequency of the gear, the resonance phenomenon will occur, causing the gear to be damaged and unable to transmit normally. Therefore, to improve the performance of each component, it is of great significance to study the response characteristics of the gear transmission system in the cutting section.

Several researches have been carried out in this field. Xun et al. studied the influence of tooth profile modification on the vibration amplitude distribution and tooth surface contact loss probability under different manufacturing tooth profile errors [1]. Geng et al. studied the dynamic characteristics of gears from the perspective of rigid-flexible coupling and nonlinearity [2, 3]. Dadon et al. proposed a general dynamic model for simulating tooth surface faults more accurately, and verified the rationality of the model by simulating and analyzing the gear transmission system with and without tooth surface faults [4]. Yi et al. found that when the gear system resonates, the spectrograms of the current and electromagnetic torque obtain recognizable characteristics [5]. Liu et al. proposed to include the calculation of all natural frequencies under different meshing conditions in the design of the transmission system, but to ignore the parameters of the meshing frequency and its frequency multiplication [6]. Jiang et al. studied the electromechanical coupling torsional vibration characteristics of the gear transmission system driven by a low-speed and high-torque permanent magnet synchronous motor, and found that the electromagnetic effect reduces the first natural frequency of the system and inhibits the vibration of the gear [7-9]. Ge et al. proposed a fuzzy control method based on active disturbance rejection and self-adaptation to suppress effectively the dynamic load of the transmission system [10]. Wang et al. analyzed the influence of damping ratio, mesh stiffness and excitation frequency of a planetary gear transmission system, and applied the research results as an analysis basis for the design of transmission system [11]. Yu et al. proposed a new calculation method for gear mesh stiffness considering the microstructure of gear teeth [12, 13]. Chen et al. established a nonlinear dynamic model of gears, and analyzed the effects of time-varying mesh stiffness, static transmission error and shaft torsional stiffness on the dynamic reliability of gears [14, 15]. Sheng et al. analyzed the effects of static excitation, dynamic, internal and external excitations on the resonance response of the transmission system[16, 17]. He et al. built a transmission system model with a combination of planetary gears and sun gears considering the influence of comprehensive deformation and dynamic meshing force [18]. Sun et al. used ADAMS, AMESim and Matlab to explore the dynamic response of a electromechanic-hydraulic system, and found that the operating height of the drum has a great influence on the maximum gear meshing force [19]. Wang et al. studied the electromechanical dynamic characteristics of the motor-gear transmission system under shock and step loads through experiments and simulations, which provided a reference for improving the dynamic performance and for monitoring the operating conditions [20]. Gao et al. proposed a method to optimize the gear transmission system, which reduced the system size and the maximum torsional acceleration of the drum and effectively reduced the manufacturing cost and failure rate [21]. By comparing the NIPPF and ANIPPF controllers, EL-Sayed et al. found that the latter more effectively suppressed the amplitude and chaotic motion of the system. The research results provided a theoretical basis for the design and construction of a shearer semi-direct drive cutting transmission system [22].

In order to better improve the performance of the gear transmission system, taking the gear transmission system of the cutting part of the shearer as the research object, the multi-rigid and rigid-flexible coupling models of the gear transmission system are established based on the Adams analysis software, and the simulation results of the multi-rigid model and the rigid-flexible coupling model are compared and analyzed. The operating conditions of the gear transmission system are simulated. Different load moments are set. The load diagram for each gear including the gear meshing force is made, and the influence law of the load torque on the transmission system is obtained.

2. Gear transmission system simulation

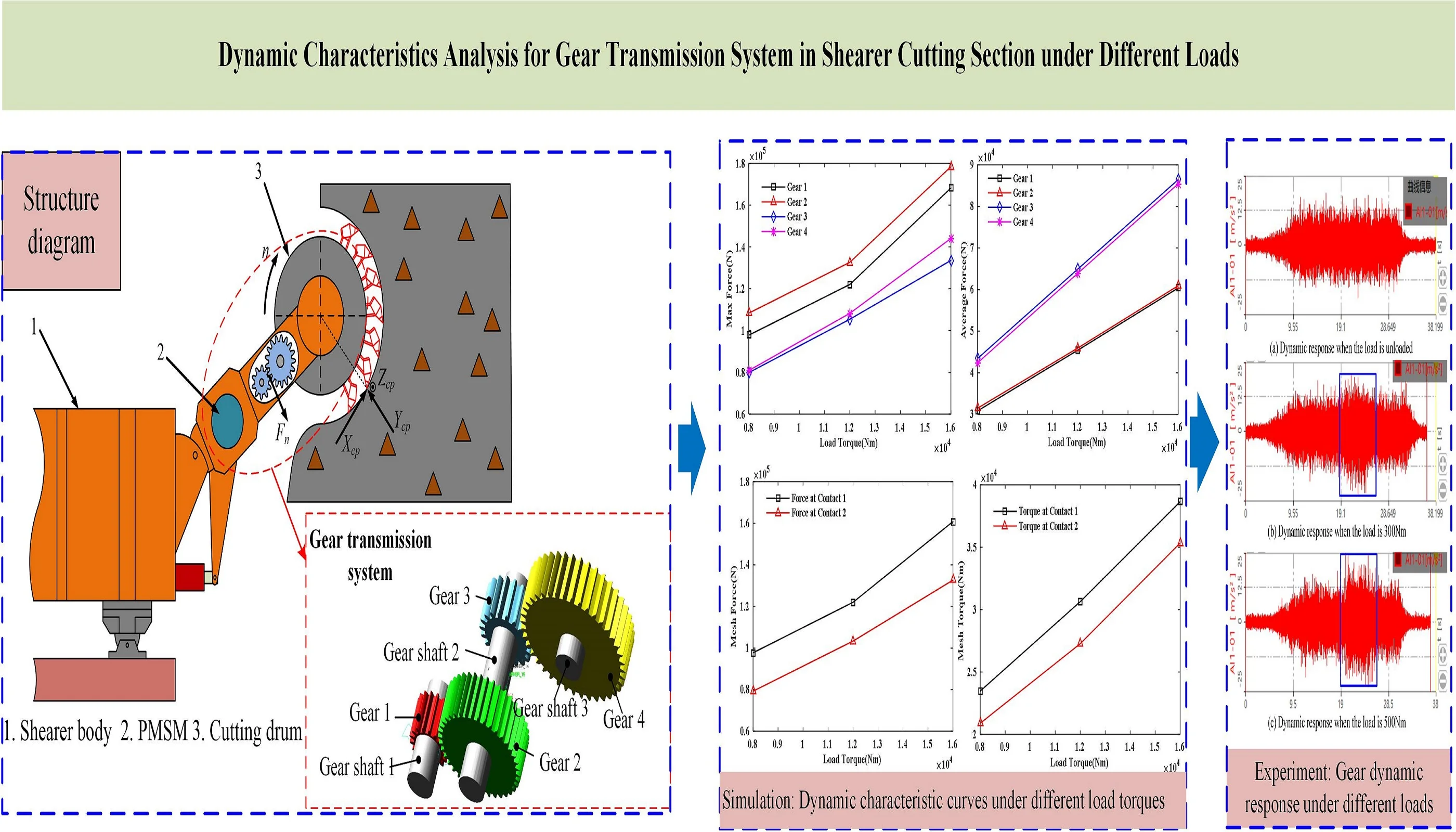
A schematic diagram of the gear transmission system in the shearer is shown in Fig. 1.

Fig. 1Schematic diagram of shearer cutting section

Shearer is mainly used for coal mining in coal mines. It mainly includes 2 pairs of meshing spur gears, 3 transmission shafts and 6 bearings. Since the huge end load is constantly changing during the coal mining process, it will directly affect the dynamic characteristics of the gear transmission system. Therefore, the research on the dynamic characteristics of the gear transmission system of the shearer cutting section has crucial significance for the overall performance improvement.

2.1. Multi-rigid body dynamics modeling

The main parameters of gears and gear shafts are shown in Table 1.

Table 1Gear and gear shaft parameters

Number	Modulus, $m$ (mm)	Number of teeth, $z$	Pressure angle, $\alpha$ (0)	Tooth width, $b$ (mm)	Gear ratio, $i$	Shaft diameter (mm)	Shaft length (mm)
1	8	17	20	110	1	100	250
2	8	39	20	100	2.294	100	550
3	10	19	20	110	2.294
4	10	40	20	100	4.83	100	250

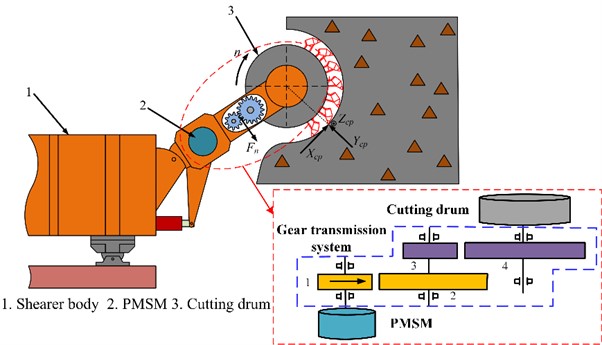
A 3D model of the gear transmission system was established using Pro/E software. Then, the 3D solid model was saved in Parasolid (*.x-t) format, and imported into the ADAMS software to build a virtual prototype model. After the model is imported, the connection constraints and contact forces between the various components are set. Gear meshing is simulated using the Impact contact function.

The Impact function expression is as follows:

1

$Impact(x,\stackrel{\cdot }{x},x_1,k,e,c_{max},d)=\left\{\begin{array}{l}Max\left[(0,k(x_1-x{)}^e-step(x,x_1-d,c_{max},x_1,0)\cdot \stackrel{\cdot }{x}\right],x<x_1,\\ 0,x\ge x_1,\end{array}\right.$

where $x$ is the distance between the two colliding objects, $\dot{x}$ is the speed of the two colliding objects, $x_1$ is the reference distance of $x$, $k$ is the stiffness coefficient of the contact surface, $e$ is the rigid force index, $c_{max}$ is the maximum damping coefficient of the contact surface, $d$ is the mutual penetration depth. When $x<x_1$, the objects touch, otherwise they do not touch.

According to the Hertzian contact theory, the contact surface stiffness coefficient is expressed as follows:

2

$k=\frac{4}{3}{R}^{1/2}{E}^{\mathrm{*}},$

where $R$ is the comprehensive radius of curvature, and $E^{\mathrm{*}}$ is the comprehensive elastic modulus.

$R$ is expressed as follows:

3

$\frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2},$

where $R_1$ and $R_2$ are the radii of the gear indexing circle.

$E^{*}$ is expressed as follows:

4

$\frac{1}{E^{\mathrm{*}}}=\frac{1-{\nu }_1^2}{E_1}-\frac{1-{\nu }_2^2}{E_2},$

where $E_1$ and $E_2$ are the Young’s moduli of the collision gear material, and $v_1$ and $v_2$ are the Poisson’s ratios of the collision gear material. The gear material is steel. The parameters of gear contacts 1 and 2 are calculated, as shown in Table 2.

Table 2Contact force parameters

Number	Material	$R_1$(mm)	$R_2$ (mm)	$R$ (mm)	$E^{*}$(N/m2)	$k$ (N/m)
Contact force 1	Steel	68	158	47.357	1.12×105	1.0277×106
Contact force 2	Steel	95	200	64.407	1.12×105	1.1985×106

Fig. 2Multi-rigid body model

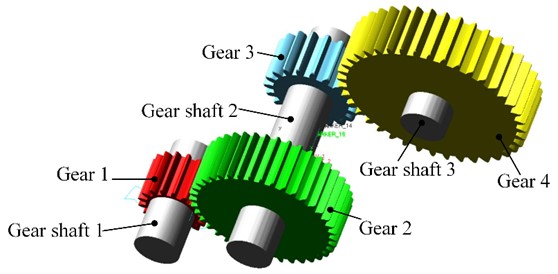
Figure 2 shows the multi-rigid body model after adding constraints and contacts. The drive rotation pair is added to shaft 1. Load torque is added to shaft 3. The applied load moment is 16000 N·m. The simulation time is set to 0.3 s, and the simulation step size is set to 2000.

Fig. 3Time history curve of transmission shaft speed

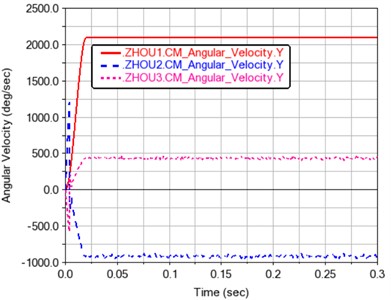
According to Fig. 3, from the direction perspective, the direction of axis 1 is positive, the one of axis 2 is negative, and finally the one of axis 3 is positive. It shows that the rotation speed of the drive shaft conforms to the law of gear transmission. From the numerical point of view, the average speed of axis 1 is 2100 d/s. The average speed of axis 2 is –915.4153 d/s, and the average speed of axis 3 is 434.8455 d/s. So, the calculation formula of transmission ratio can be expressed as follows:

5

$i=\frac{n_1}{n_2},$

where $i$ is the transmission ratio, $n_1$ is the speed of the input shaft, and $n_2$ is the speed of the output shaft. According to the average speed of each axis, $i_1=$2.294, $i_2=$4.829, which shows that the transmission ratio in the model is very close to the theoretical transmission ratio. It also shows that the established multi-rigid body dynamic model is reliable and reasonable.

Fig. 4 shows the total meshing force of the gears. It can be seen that after the transmission is stabilized, the meshing force of the gears makes them mesh and disengage regularly with the rotation of the gears. The main reason is that the second pair of gears is closer to the end load. The impact is even greater. It shows a variation law that fluctuates around the mean value.

Fig. 4Time history curve of meshing force

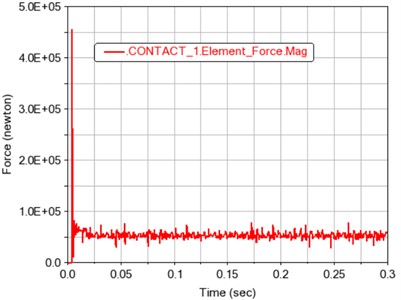
a) Contact 1 total meshing force

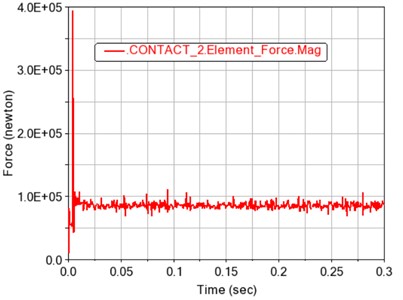
b) Contact 2 total meshing force

2.2. Rigid-flexible coupling dynamics simulation

Due to that the small deformations will occur when the gears mesh, because the gear is a flexible body, and this deformation will further cause the force and load changes of the gear during the gear meshing process. Based on the ADAMS/Viewflex module, the rigid body of the gear is converted into a flexible body. After the gear becomes flexible, it is necessary to delete the rigid contact and change it into the flexible contact. The unit sizes of gear 1, gear 2, gear 3, and gear 4 are uniformly set to 10 mm. After the ADAMS flexibility processed, the unit numbers of gear 1, gear 2, gear 3, and gear 4 are 2638, 9928, 4386, and 13594 respectively.

Consistent with the multi-rigid body model, the load moment is set to 16000 N·m. The simulation time is 0.3 s, and the simulation step is 2000. The simulation results are shown in Fig. 5.

Fig. 5Time history curve of transmission shaft speed

According to Fig. 5, from the direction perspective, the direction of axis 1 is positive, the direction of axis 2 is negative, and the direction of axis 3 is positive, which indicates that the rotation speed of the transmission shaft conforms to the law of gear transmission. From the numerical point of view, the average speed of axis 1 is 2100 d/s. The average speed of axis 2 is –918.2197 d/s, and the average speed of axis 3 is 435.1158 d/s. According to the average speed of each axis, $i_1=$2.287, $i_2=$4.826, which shows that the transmission ratio in the model is very close to the theoretical transmission ratio.

Table 3Theoretical speed and actual speed table of each drive shaft

Number	Theoretical speed, d/s	Multiple rigid body average speed, d/s	Rigid-flexible coupling average speed, d/s
Gear shaft 1	2100	2100	2100
Gear shaft 2	–915.4316	-915.4153	–918.2197
Gear shaft 3	434.7826	434.8455	435.1158

Table 3 shows the theoretical speed and actual average speed of the drive shaft before and after the flexible body of the gear. It can be seen from the table that the average rotational speed of each driven shaft increased after the gear became flexible. Comparing Fig. 5 and Fig. 3, it can be found that the rotational speed of each transmission shaft fluctuates more after the gear became flexible, and the calculated actual value of the transmission ratio is also larger than the theoretical value. This is because in the actual transmission process, the gears have non-ideal meshing due to problems such as deformation and impact, which makes the difference between the instantaneous transmission ratio and the theoretical transmission ratio.

Fig. 6Contact 1 gear total meshing force

a) Time curve of total meshing force

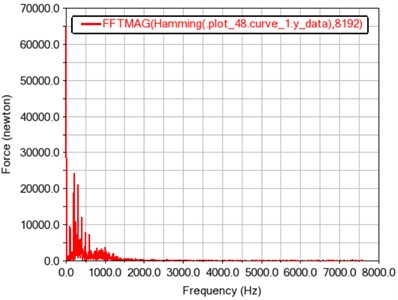
b) Frequency curve of total meshing force

From the time history curve of gear meshing force depicted in Fig. 6(a), it can be concluded that the gear meshing force of contact 1 fluctuates around its average value of 64782.8524 N. The fluctuation period and the fluctuation range are generally presented as a stable value, which is also in line with the periodic meshing motion law of the gear teeth. As it can be seen from the spectrogram depicted in Fig. 6(b), the peak points are located at frequencies of around 99, 198, 297, and 396 Hz, and the maximum amplitude occurs at around 198 Hz.

The meshing frequency equation is as follows:

6

$f_z=\frac{z\bullet n}{60},$

where $f_z$ is the meshing frequency, $z$ is the number of gear teeth, and $n$ (r/min) is the rotational speed.

According to the Eq. (6), the theoretical meshing frequency is calculated as $f_z=$99.17. The frequencies shown in Fig. 6(b) are multiples of the theoretical meshing frequency.

The meshing force of the contact 2 gears fluctuates up and down around its average value of 90719.7409 N, and the fluctuation period and fluctuation range are roughly a stable value, which is also in line with the periodic meshing motion of the gear teeth.

Fig. 7Contact 2 gear total meshing force

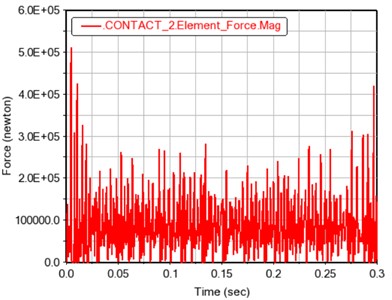
a) Time curve of total meshing force

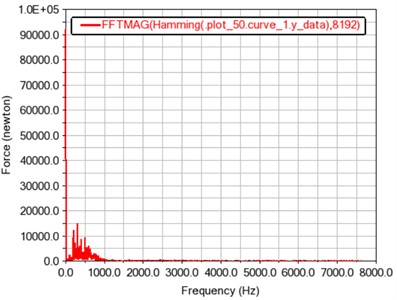
b) Frequency curve of total meshing force

From Fig. 7(b), it is found that the peak points also occur at frequencies of around 99, 198, 297, and 396 Hz, and the maximum amplitude occurs at around 297 Hz. In summary, the rigid-flexible coupling model can also provide a reference for a further research on the dynamic characteristics of gears.

3. Dynamic simulation under different loads

Due to the existence of uneven coal seam, gangue and coal rock mass, the load applied at the cutting section during coal mining works fluctuates, so the dynamic characteristics of the transmission system shall be studied in depth. As a result, different load moments of 8000 N·m, 12000 N·m, 16000 N·m and step load moments are set. The input shaft speed is set to 350 rpm, and a drive function is added to the rotating pair of axis 1. Table 4 shows the maximum load of each gear under different load moments. Table 5 shows the average load of each gear under different load moments. Table 6 shows the meshing force and moment at the contact point of different load moments.

According to Table 4, Table 5, and Table 6, the dynamic characteristic curves of Fig. 9 under different load moments are drawn.

It can be seen from Fig. 8(a) and 8(b) that the maximum load and average load on each gear increase with the increase of the load torque. It can be seen from Fig. 8(c) and 8(d) that the maximum gear meshing force and meshing torque also increase with the increase of the load torque.

Fig. 8Dynamic characteristic curves under different load torques

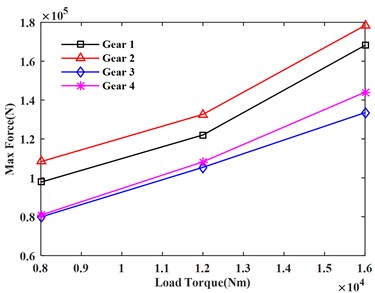
a) Maximum load

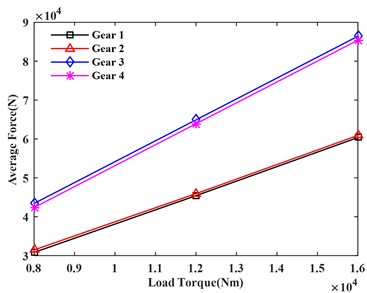
b) Average load

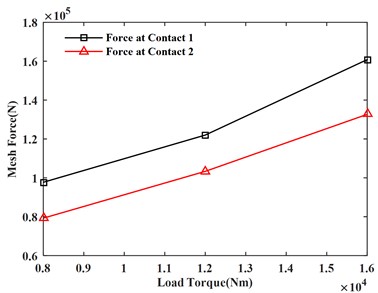
c) Meshing force

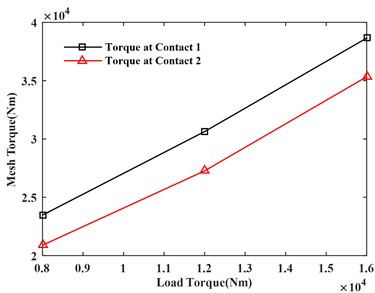
d) Meshing torque

In order to observe the fluctuations of gear dynamic characteristics under continuous load changes, step functions were integrated and applied to the load curve, as shown in Fig. 9. The simulation results are shown in Figs. 10-13.

Fig. 9Load torque

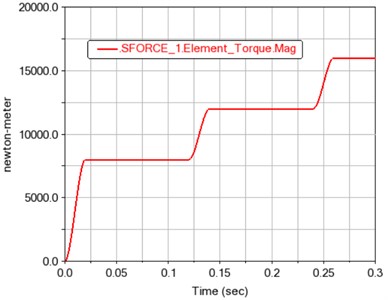
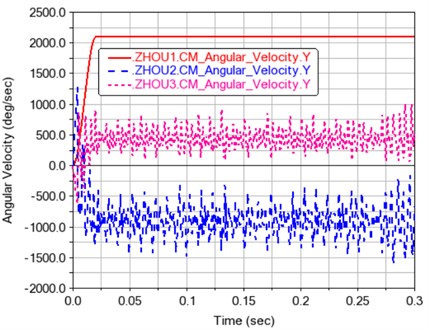
Fig. 10Variation curve of angular velocity of each gear

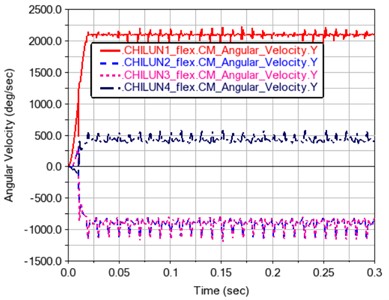
It can be seen from Fig. 10 that after the operation has been stabilized, the average speed of gear 1 becomes 2100.1936 d/s. The average speed of gear 2 is –915.3471 d/s. The average speed of gear 3 is –915.084 d/s, and the average speed of gear 4 is 435.0932 d/s.

Fig. 11 shows the force of gears 1~4. It can be seen from the force time history figure that the gear force is positively correlated with the load. It also shows that the simulation of gear transmission system created in the Adams software is simple and reliable.

Fig. 11Load time history curve of each gear

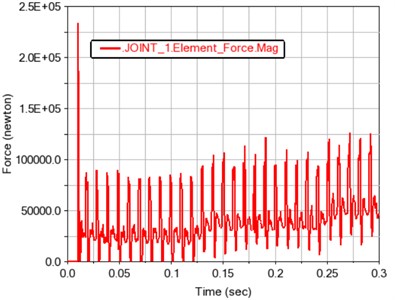
a) Gear 1

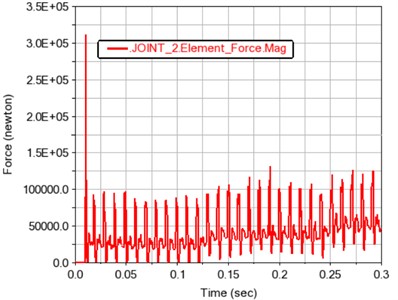
b) Gear 2

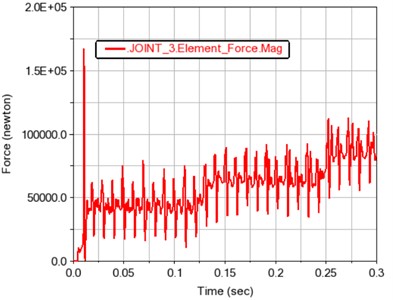
c) Gear 3

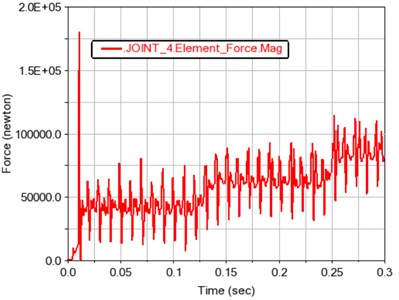
d) Gear 4

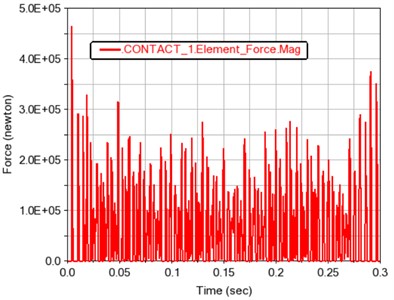
Fig. 12 and 13 show the meshing force and moment of gears 1, 2 and 3, 4 after contact, respectively. The contact force and contact torque are also positively correlated with the load fluctuation, and conform to the relationship of the transmission ratio.

Fig. 12Time history curve of gear meshing force and torque in contact 1

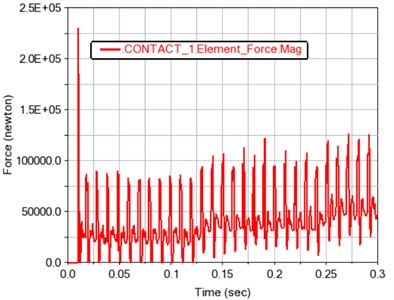
a) Gear meshing force

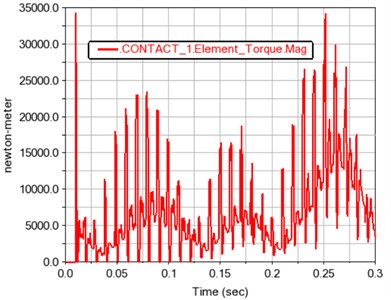
b) Gear meshing torque

Fig. 13Time history curve of gear meshing force and torque in contact 2

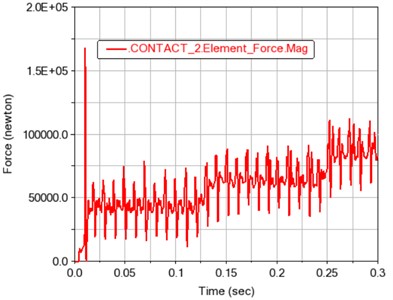
a) Gear meshing force

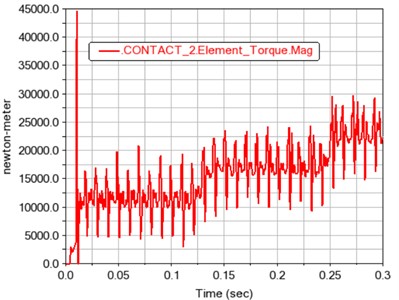
b) Gear meshing torque

Fig. 14Experimental layout of semi-direct drive gear transmission system

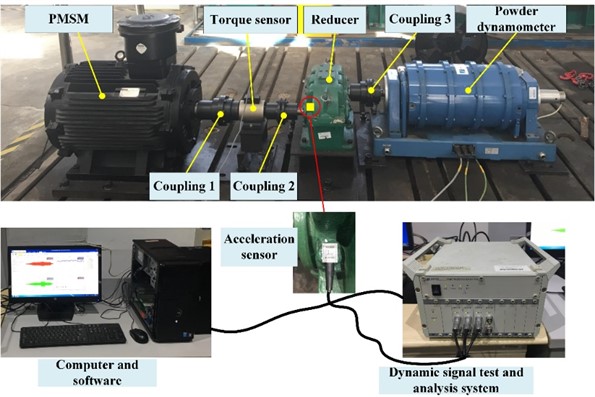
Fig. 15Relationship between speed and time of PMSM

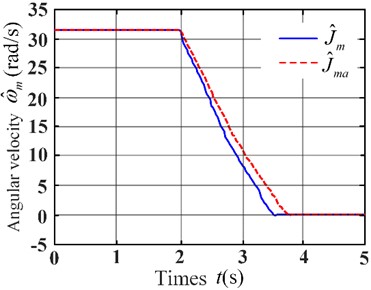
To verify the correctness of the simulation results, a small test bench for the proportional load simulation was built, as shown in Fig. 14. According to the principle of small-size parameter scaling and the deceleration method of inertia identification, the permanent magnet motor had been started to the rated speed and then stopped freely. The data of free stop of permanent magnet motor under no-load state and flywheel state with known inertia $J_a=$0.262 kg·m² were recorded. According to the obtained data, the relationship curve between speed and time was drawn, as shown in Fig. 15.

According to the relationship between speed and time in Fig. 15, data of different time stages were intercepted respectively, as shown in Table 7.

According to the data from Table 7, the load similarity coefficient of the system was calculated as 71.6. The final load torque fluctuated around 16000 N·m, so the actual final load should fluctuate around 16000N·m/71.6 = 223.46 N·m. The acceleration sensor was installed at the reducer of the small proportion load simulation test platform, and the test position of the acceleration sensor is installed at the external box close to the first stage gear, as shown in Fig. 14.

Fig. 16Gear dynamic response under different loads

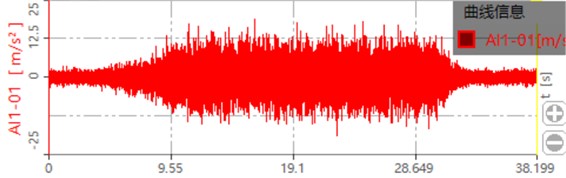
a) Dynamic response when the load is unloaded

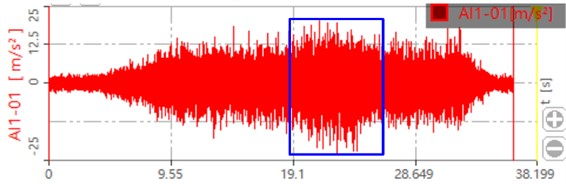
b) Dynamic response when the load is 300 Nm

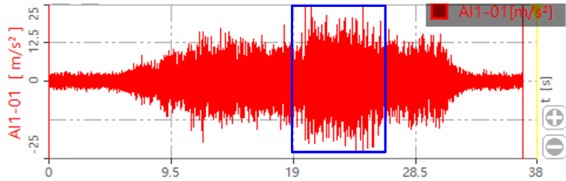
c) Dynamic response when the load is 500 Nm

The collected dynamic signal is transferred to the dynamic signal test and analysis system. The dynamic response of the gear after processing is shown in Fig. 16. The blue box in the figure shows the dynamic response of the gear after loading. It can be seen that when the load is zero, the maximum value is around 15 m/s². When the load is 300 Nm, the maximum value is around 20 m/s². When the load is 500 Nm, the maximum value is around 25 m/s². This is also consistent with the loading trend of the simulation, which proves that the contact force and dynamic response of the system increase with the increase of the load.

4. Conclusions

The geometric model of the gear cutting transmission system in shearer was established by using the 3D modeling software Pro/E. The dynamics of the gear transmission system under different loads were simulated and analyzed in the ADAMS software. To be close to the actual operating condition of the gear transmission system, it was set flexibly. The research results showed that the speed fluctuation had raised after the gear had become flexible. The gear meshing force was positively related to the load. They also demonstrated that the analysis of the dynamic characteristics of the gear in the Adams software was correct and reliable. At the same time, the detailed modeling process was given in this paper, which could provide a reference for the subsequent co-simulation of the electromechanical coupling model.