Abstract
The conventional eigenvalue alarm mode has a high rate of false alarm and missed alarm for the low-speed heavy load super large rolling bearing. Besides, the traditional signal processing method such as envelope spectral analysis is difficult to extract its fault characteristic frequencies, resulting in a high rate of false diagnosis and missed diagnosis. In order to solve the above problems, an intelligent diagnosis method for the low-speed heavy load super large rolling bearing based on deep learning is proposed. The proposed method mainly utilizes the strong robustness of deep learning algorithm to the quality of original vibration data in the field of fault diagnosis. Firstly, an effective signal acquisition scheme is designed to solve the problem that the signal characteristics of low-speed heavy load super large rolling element bearing are difficult to be acquired. Then, the collected data are randomly divided into training sets, verification sets and test sets by using data enhancement technology. Subsequently, input the divided training set samples into 1-dimensional convolution neural network (1DCNN) deep learning model for learning and training to construct the 1DCNN learning model and set network structure parameters. Meanwhile, the optimal training model is obtained by validating the updating effect of model parameters through validation set. Finally, the test data is input into the trained model to realize intelligent diagnosis. Effectiveness of the proposed method is verified by the vibration data of a wind power main bearing.
Highlights
- Aiming at the problem that it is difficult to collect the characteristics of low-speed heavy load bearing' vibration signal, a simple and effective hardware acquisition scheme is designed
- An effective 1DCNN model is trained and is suitable for fault diagnosis of low-speed heavy load super large rolling element bearing
- The proposed method has high diagnostic accuracy and could provide a new idea for the diagnosis of low-speed heavy load super large rolling element bearing
1. Introduction
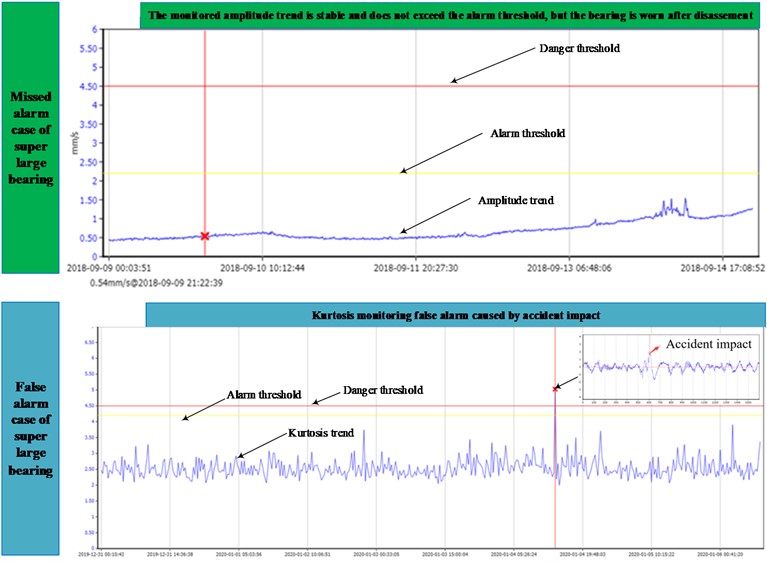
The super large rolling bearing refers to the bearing with a nominal outer diameter of more than 440 mm [1], which is used widely in energy, building materials, engineering construction and other fields. For example, the rolling element bearing used in the coal mill, the pitch bearing used in the wind turbine, and the main bearing used in the tunnel boring machine (TBM) are all super large rolling element bearings. Compared with conventional rolling element bearings, the type of rolling element bearing studied in the paper not only has common characteristics of huge size, low rotating speed, heavy load, slow change of fault features, but also has similar fault mechanism. In practical engineering, it is often no longer applicable to judge its running states based on conventional threshold alarm monitoring methods such as vibration amplitude, kurtosis index, etc. Fig. 1 presents the typical false and missed alarm cases of super large bearing based on conventional threshold alarm method in practical engineering application, and the above figure is a missed alarm event: the monitored vibration amplitude trend of a low-speed heavy load bearing does not exceed the alarm limit. However, it was found that serious wear failure had occurred when the machine is shut down and disassembled. The below figure shows a false alarm event caused by additional shock, which results in kurtosis alarm. Envelope spectral analysis based on resonance principle is one of the traditional classical methods for fault diagnosis of rolling element bearing by extracting the fault characteristic frequencies effectively. Unfortunately, it would not work effectively on large rolling bearing running at low-speed. The main reason is that the fault in any parts (inner race, outer race, rolling element or cage) will lead to series of impacts whenever a rolling element comes in contact with the fault, and the energy of impacts is too weak under low speed to excite the resonance of the entire system including the bearing housing, sensors and structure on which the bearing is mounted. In the past decade, kinds of advanced signal processing techniques such as minimum entropy de-convolution [2], spectral kurtosis [3], higher order spectral technique [4], wavelet analysis [5-7], empirical mode decomposition [8-9], wavelet de-noising [10-11], wavelet decomposition tree [12], etc. have been proposed. However, the above-mentioned signal processing methods still would not give satisfactory diagnosis effect when the rotor supported by the super large bearing rotates at low speed, and the reason is still that the impulse strength caused by the fault is too weak [13].
Fig. 1False and missed alarm cases of super large bearing
Generally, the rotating speed of rolling element bearing below 100 RPM could be considered as low speed [13]. In this paper, the rotating speed of the studied object is much lower, that is about 15 RPM. Although domestic and foreign scholars have made some progress in the research of fault diagnosis of low-speed heavy load super large rolling element bearing, especially in its structural mechanics research [14-16], testing and monitoring technology research [17-18], life prediction research [19-22], etc., the new monitoring technology in theoretical research is still far from mature and effective engineering application. In addition, the life prediction of super large rolling element bearing is mainly based on cumulative damage experiments or classic life calculation models, whose theory novelty is relatively limited. Intelligent diagnosis of low-speed heavy load super large rolling element bearing is an effective solution to the above problems, which focuses mainly in two directions: 1) Intelligent diagnosis based on shallow machine learning. 2) Intelligent diagnosis based on deep learning. As for the first direction, to achieve high classification accuracy, shallow machine learning is mainly based on effective feature extraction, and then uses the extracted feature vector as the training and test set of intelligent algorithms such as back propagation neural network (BP), support vector machine (SVM), support vector data description (SVDD), hidden Markov model (HMM), etc. [15, 23-25]. Normally, shall machine learning has the disadvantages of requiring high-quality raw data and effective feature extraction algorithm. The second direction has become the current mainstream. At present, various deep learning algorithms have been used widely in fault diagnosis [26-32]. In view of the characteristics that deep learning does not require feature extraction and has strong robustness to the quality of original data, as well as the weak features caused by the complex operating conditions and slow change of features in the operation process of low-speed heavy load super large rolling element bearing, a corresponding intelligent diagnosis method is proposed. Main contributions of the paper are as follows: 1) Aiming at the problem that it is difficult to collect the characteristics of low-speed heavy load bearing’ vibration signal, a simple and effective hardware acquisition scheme is designed. 2) An effective 1DCNN model is trained and is suitable for fault diagnosis of low-speed heavy load super large rolling element bearing. 3) The proposed method has high diagnostic accuracy and could provide a new idea for the diagnosis of low-speed heavy load super large rolling element bearing. Besides, its advantage over the other shallow machine learning methods is also verified.
The rest of the paper is organized as follows: Section 2 is dedicated to the theory of 1DCNN, and flow chart of the proposed method with its details are described in Section 3. Experiment verification is given in Section 4 and conclusion is obtained in Section 5 at last.
2. 1DCNN
CNN is one kind of deep learning, which extracts deep feature information layer by layer through convolution and pooling. At present, it could be divided into two types in view of input signals: 1DCNN and 2DCNN. The input of 2DCNN is two-dimensional image data, and if the signal collected by sensor in actual project is one-dimensional time signal, which needs to be converted into two-dimensional signals by certain methods such as short-time Fourier transform, wavelet transform, etc. During such conversion process, it could not be guaranteed whether there will be distortion, or even the risk of loss of useful information. Besides, the network layer of 2DCNN is relatively more complex, and the above-mentioned shortcomings of 2DCNN may lead to insufficient feature learning in the training and learning of network model, resulting in decline of accuracy. 1DCNN takes one-dimensional signal as input directly, which could ensure that it contains all the characteristic information of the original signal and avoids the above problems of 2DCNN. 1DCNN is a forward propagation artificial neural network, whose network parameters are updated by the back propagation algorithm [33]. Compared with 2DCNN, its network structure is simple and compact, and it can effectively carry out classification training with limited data. Flow chart of the used 1DCNN is shown in Fig. 2, whose main structure is mainly composed of convolution layer, activation layer and pooling layer.
Fig. 21DCNN flow diagram
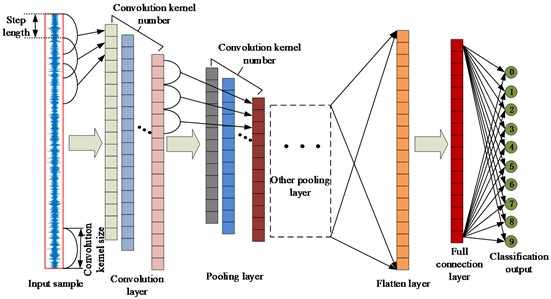
2.1. Convolution layer
The convolution layer uses the given convolutional kernel to convolute the input features, and extracts the obvious fault impact features. It involves multiple feature maps with multiple neurons, and each neuron of each feature map is connected with the local area of the previous feature map through a set of weights. The local area is called the receptive field of neurons, and the group of weights is called convolution kernel. CNN could realize weight sharing when the same convolution kernel is used to calculate the input features, and weight sharing could reduce network complexity and avoid over-fitting problem. The calculation equation of convolution layer is given in Eq. (1):
where xij is the output feature of the lth layer, f represents activation function, Mj is the input feature map, xl-1i is the input information of the lth layer, wlij is the convolution kernel weight and blj is offset.
2.2. Activation layer
The activation layer is mainly used for nonlinear transformation of convolution features by using activation functions, which enhances the representation ability of features, thus making it easier for the network to distinguish the features of different fault types. The Relu activation function shown in Eq. (2) is used in the paper:
where x is the output of convolution layer, and y is the activated value of x.
2.3. Pooling layer
After the convolution and activation operations of the input features, the noise interference could be eliminated to a certain extent through the pooling operation to increase the stability of the features. The pooling layer plays the role of down-sampling operation, and can aggregate the obtained features, so that similar features can be combined into one, which is used to reduce the dimension of features. In this experiment, the maximum pooling operation is used to locally maximize the perception domain of the output feature information, so as to obtain more representative features and avoid over-fitting:
where qli(t) is the value of thetthneuron in the ith feature map in the lth layer. pl+1i is the value of the (l+1)th layer neuron. W is pooling width, and j is the size of sliding step.
2.4. Full connection layer and output layer
The pooled feature will go through the full connection layer to integrate the extracted feature information, and then classify and diagnose the forward calculated value through the activation function. Among them, the activation function of the last layer is the Softmax function, which could normalize the probability distribution of different types of fault characteristics, and compress any real value vector into the value range [0, 1). The closer the value is to 1, the more likely the output is the actual fault type.
The training and learning processes based on 1DCNN network model have five convolution stages for feature extraction, and each convolution stage contains a set of one-dimensional convolution layers for learning the characteristics of input signal. Batch normalization layer normalizes the feature vector of a batch output to appropriate data distribution, making the output value more stable, thus accelerating the model learning speed. The nonlinear unit activation function (Relu) performs nonlinear transformation on the extracted signal features to overcome the problem of gradient disappearance and accelerate the training speed. The maximum pooling layer is used to improve the local translation invariance characteristics of the input signal. The first convolution layer in the network model uses a wide convolution kernel to suppress the high-frequency noise in the input signal and capture the remote correlation features, while the other convolution layers use a smaller convolution kernel to obtain the complex representation of the characteristics of the input signal. The number of convolution kernel in the output layer, that is, the number of neurons, is determined by the type of state of the experimental data. In this paper, ADAM optimizer is used to update and optimize the weight and bias of the network. Softmax classifier is used as the classifier, and the evaluation standard is accuracy.
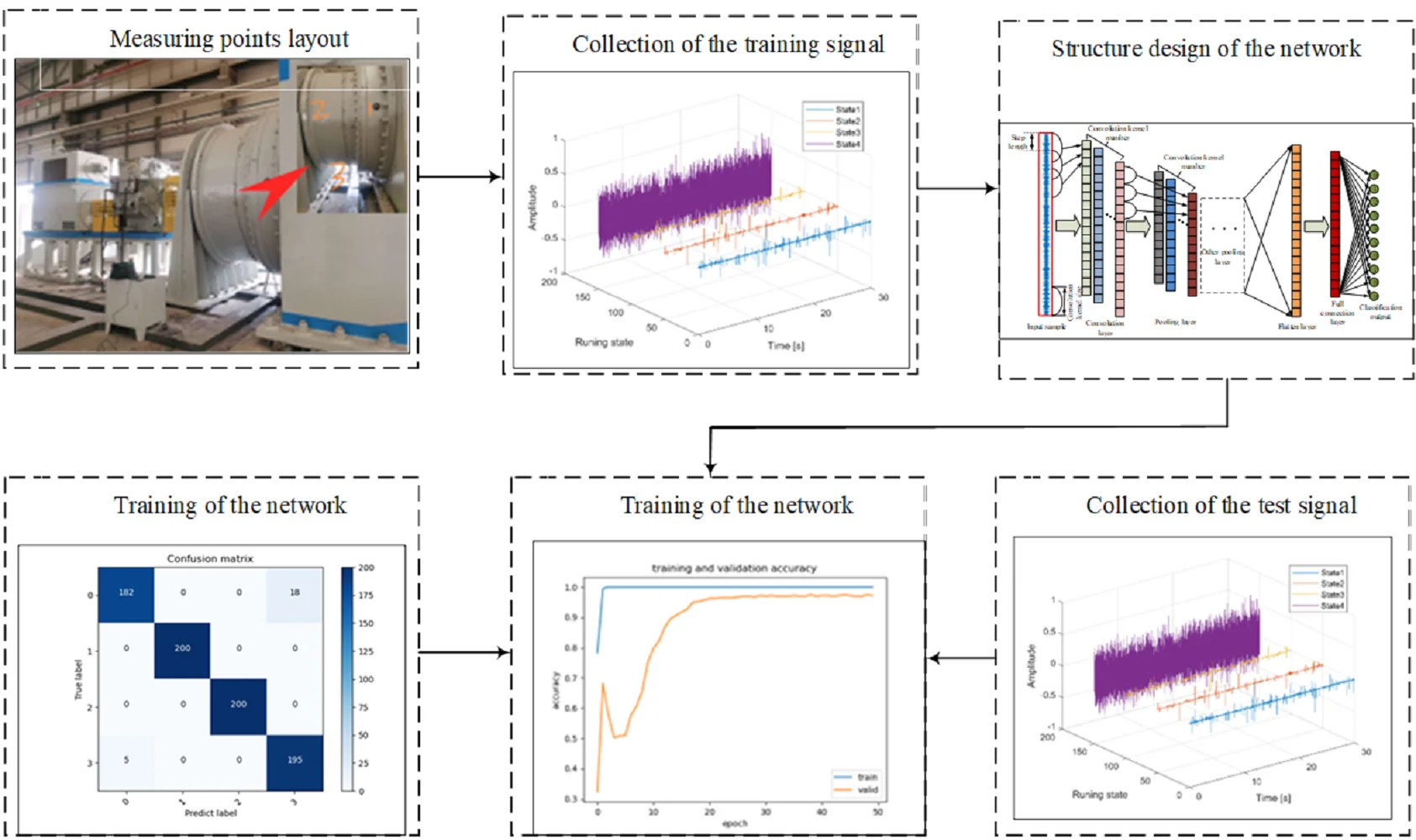
3. Flow chart of the proposed method with its details
The concrete steps of the proposed method are as following:
Step 1: Signal collection: acceleration sensor is used to collect the vibration signal data of low-speed heavy load super large rolling bearing under various known fault conditions and normal condition.
Step 2: Sample division: set the sample length and use data enhancement technology to divide the collected vibration data randomly to obtain sample data, including training set, verification set and test set.
Step 3: Build deep learning model and conduct training, and save the optimal model: build one learning model and set network structure parameters by using 1DCNN, then input the divided training set samples into the 1DCNN deep learning model for learning and training, and verify the updating effect of model parameters through the validation set to obtain the optimal training model.
Step 4: Real-time evaluation: input the test data of low-speed heavy load super large rolling bearing into the above trained learning model to obtain the fault diagnosis results, and the final model parameters are saved. The vibration data of low-speed heavy load super large rolling bearing under unknown fault states is collected in real time, and the 1DCNN deep learning model is used for real-time fault detection to realize intelligent fault diagnosis.
In step 1, the signal acquisition scheme is shown in Fig. 3 in view of the weak and slow change characteristics of the vibration signal of low-speed heavy load super large rolling bearing: compared with the signal acquisition scheme of ordinary bearing, the charge amplifier is added between the acceleration sensor and the collector in addition to use the high sensitivity vibration sensor. At the same time, the sampling parameters need to be set with low sampling frequency and long sampling length.
Fig. 3Signal acquisition strategy

In step 2, as for the samples under each fault state, 70 % of the samples are randomly selected as the training set, 10 % as the verification set, and the remaining 20 % as the test set: set the length of sample data as L firstly. Assume that the total length of one-dimensional original fault data under one kind of fault state of the low-speed heavy load super large rolling bearing is X, then set a random number i in the range (0,X-L), and use data enhancement method of fixed-length random segmentation to segment the original vibration data to obtain n samples. The data enhancement method could enhance the randomness of the sample data, thus increasing the robustness of the model. Use same method to obtain the sample data under other fault conditions to form the original data set, and divide the original data set according to the set ratio.
4. Experiment verification
The experimental object is a main bearing of a wind power plant, whose actual picture is given in Fig. 4. Five measuring points are arranged for the main bearing as shown in Fig. 5 to collect the vibration signals using different sampling parameters, and the details of the sampling settings and sampled values are presented in Table 1. It should be noted that measuring points 1 and 2 are two sensors arranged in 90 degrees at the same monitoring position. The rotating speed of main bearing is 15 r/min, and the acceleration sensor is selected to be placed on measuring point 3, namely the main loading area through analyzing and comparing the time domain diagram, spectrum diagram and envelope spectrum diagram of the vibration data collected from the different measuring points shown in Fig. 5. Besides, it is more reasonable to set the sampling frequency and sampling length as 128 Hz and 16384 points respectively through comparing.
Table 1Details of the sampling parameters with the measured vibration amplitudes
Measuring points | Rotating speed (r/min) | Sampling frequency (Hz) | Sampling length (Points) | Vibration amplitude (m/s/s) |
1 | 15 | 256 | 512 | 0.02 |
4096 | 0.02 | |||
8192 | 0.02 | |||
16384 | 0.02 | |||
32768 | 0.02 | |||
2 | 15 | 256 | 512 | 0.02 |
4096 | 0.02 | |||
8192 | 0.02 | |||
16384 | 0.02 | |||
32768 | 0.02 | |||
3 | 15 | 256 | 512 | 0.3 |
4096 | 0.3 | |||
8192 | 0.3 | |||
16384 | 0.32 | |||
32768 | 0.32 | |||
4 | 15 | 256 | 512 | 0.01 |
4096 | 0.01 | |||
8192 | 0.01 | |||
16384 | 0.01 | |||
32768 | 0.01 | |||
5 | 15 | 256 | 512 | 0.01 |
4096 | 0.01 | |||
8192 | 0.01 | |||
16384 | 0.01 | |||
32768 | 0.01 |
The signal acquisition scheme is used to collect the one-dimensional original fault signals of the test bearing in four states (state 1: outer race fault; state 2: inner race fault; state 3: cage fault; state 4: normal), and their time-domain waveform are given in Fig. 6. The envelope spectral analysis results corresponding to the four running states are shown Fig. 7. The fault characteristic frequencies of outer race, inner race and cage could be calculated respectively using the corresponding calculation formulas. However, the above fault characteristics frequencies could not be reflected in Fig. 7 through comparison, which shows that the conventional envelope spectral feature extraction method is invalid in the diagnosis of low-speed heavy load super large rolling bearing. Complete the training of 1DCNN model and save the final model parameters. The model is used to classify the vibration signals of the experimental bearing in real time, and the sample data set and sample division are shown in Table 2.
Fig. 4The test rig

Fig. 5The five different measuring points
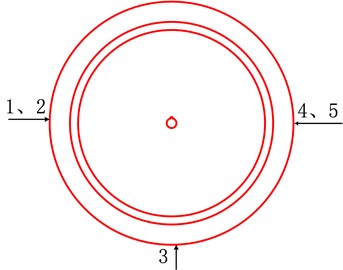
Fig. 6Time domain waveforms of the test bearing’ running states
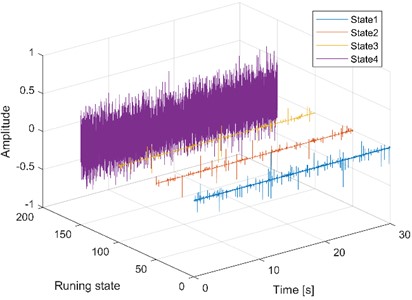
Fig. 7Envelope spectral analysis results of the four states
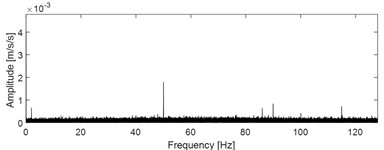
a) Envelope spectrum of running state 1
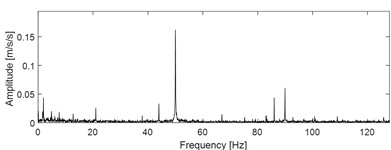
b) Envelope spectrum of running state 2
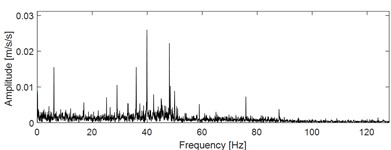
c) Envelope spectrum of running state 3
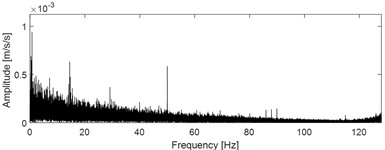
d) Envelope spectrum of running state 4
Fig. 8 shows the classification accuracy and loss function values obtained by 1DCNN network model after 50 iterations. The experimental results show that this method could converge to obtain higher accuracy and less loss results with only a few iterations, indicating that the network model designed by this method is more reasonable. The structural parameters of the fault diagnosis model are presented in Table 3.
Table 2Sample data set and sample division
Running states | State 1 | State 2 | State 3 | State 4 |
Label | 0 | 1 | 2 | 3 |
Data length | 512 | 512 | 512 | 512 |
Training samples | 700 | 700 | 700 | 700 |
Verification samples | 100 | 100 | 100 | 100 |
Test samples | 200 | 200 | 200 | 200 |
Fig. 8Curves of training relating to accuracy and validation loss
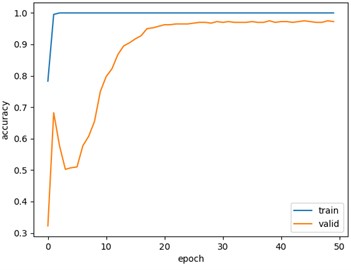
a) Curve of training relating to accuracy
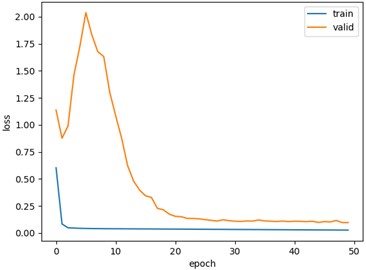
b) Curve of training relating to validation loss
Table 3Structure parameters of the 1DCNN fault diagnosis model
Model structure | Convolution kernel | Number of convolution kernel | Step length |
Convolution layer 1 | 16 | 16 | 2 |
Pooling layer 1 | 16 | 2 | 2 |
Convolution layer 2 | 32 | 3 | 1 |
Pooling layer 2 | 32 | 2 | 2 |
Convolution layer 3 | 64 | 3 | 1 |
Pooling layer 3 | 64 | 2 | 2 |
Convolution layer 4 | 64 | 3 | 1 |
Pooling layer 4 | 64 | 2 | 2 |
Convolution layer 5 | 64 | 3 | 1 |
Pooling layer 5 | 64 | 2 | 2 |
Full collection layer | 1 | 100 | – |
Output layer | 1 | 4 | – |
Fig. 9 shows the confusion matrix diagram of classifying the data set in four states based on 1DCNN model. The confusion matrix could record the classification details of each state labeled 0-3, including the classification accuracy and misclassification number. The dark area on the diagonal of the confusion matrix represents the accuracy rate corresponding to each type of fault, 200 is the number of test sets for each type of fault, and the values in other areas are the number of misclassifications, and it could be seen that the 1DCNN model has a high accuracy rate, up to 97.13 %, which shows that the proposed method could be better applied on the fault diagnosis of low-speed heavy load super large rolling bearing, and could provide great feasibility.
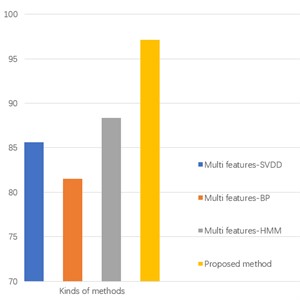
The three kinds of traditional machine learning methods (Multi features-SVDD, Multi features-BP, Multi features-HMM) are used for comparison, and the Multi features include standard deviation, peak, skewness, kurtosis, crest factor, shape factor. The comparison results of the four intelligent diagnosis methods are shown in Fig. 10: the quantitative comparison shows that the proposed method has higher diagnostic accuracy. The main reason is that the diagnosis accuracy of the traditional intelligent diagnosis algorithm mainly depends on the effective feature vector, while the operation condition of the low-speed heavy load bearing is different from that of the conventional bearing, and the corresponding traditional time-domain features could not reflect its real operation characteristics effectively, resulting in the subsequent unsatisfactory diagnosis accuracy.
Fig. 9Classification ratio of the confusion matrix
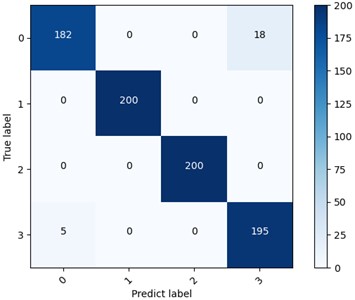
Fig. 10Comparison results using different methods
5. Conclusions
In the paper, an intelligent diagnosis method for low-speed heavy load super large rolling bearing based on 1DCNN is proposed systematically, and its effectiveness is verified by relevant experiment on the main bearing test bench of wind power pitch. The specific conclusions are as follows:
1) To solve the problem that the signal characteristics of low-speed heavy load super large rolling bearing change slowly and are difficult to be collected, a charge amplifier could be installed between the high-sensitivity sensor and the signal collector. It is more effective to collect the vibration signals in the bearing aera to reflect the fault characteristics by analyzing and comparing the time domain characteristics of vibration signals at different measuring points.
2) The conventional effective feature extraction method of rolling bearing-envelope spectral analysis method is no longer applicable to fault characteristic frequency extraction of low-speed heavy load super large rolling bearing. The reason is that faults in any parts (inner race, outer race, rolling elements, cage) of the low-speed heavy load super large rolling bearing could lead to a series of impacts whenever a rolling element comes in contact with a fault. Unfortunately, the impulses generated by these impacts could not excite the entire system that includes bearing housing, sensors and structure on which the bearing is mounted due to the low rotating speed.
3) 1DCNN deep learning is used and constructed in the paper with the corresponding network structure parameters being set. The divided training set samples are input into the constructed 1DCNN model for learning and training, then the updating effect of the model parameters is verified by the validation set, and the optimal trained model suitable for low-speed heavy load super large rolling bearing could be obtained.
4) The obvious degree of characteristics of the vibration data of the main bearing area of the low-speed heavy load super large rolling bearing is more ideal than the other areas through analyzing and comparison. By increasing the amount of basic information contained in the data and combining with 1DCNN deep learning algorithm to extract the features of the original vibration signal automatically, the intelligent recognition bearing fault mode could be realized, and the recognition accuracy is up to 97 %.
The proposed method could provide a new idea for the diagnosis of engineering low-speed heavy super large rolling element bearing.
References
-
S. E. Deng, Q. Y. Jia, and J. X. Xue, Design Principle of Rolling Element Bearing (Version 2). Beijing: China Standards Press, 2014.
-
N. Sawalhi, R. B. Randall, and H. Endo, “The enhancement of fault detection and diagnosis in rolling element bearings using minimum entropy deconvolution combined with spectral kurtosis,” Mechanical Systems and Signal Processing, Vol. 21, No. 6, pp. 2616–2633, Aug. 2007, https://doi.org/10.1016/j.ymssp.2006.12.002
-
J. Antoni and R. B. Randall, “The spectral kurtosis: application to the vibratory surveillance and diagnostics of rotating machines,” Mechanical Systems and Signal Processing, Vol. 20, No. 2, pp. 308–331, Feb. 2006, https://doi.org/10.1016/j.ymssp.2004.09.002
-
I. M. Howard, “Higher-order spectral techniques for machine vibration condition monitoring,” Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, Vol. 211, No. 4, pp. 211–219, Apr. 1997, https://doi.org/10.1243/0954410971532622
-
P. W. Tse, Y. H. Peng, and R. Yam, “Wavelet analysis and envelope detection for rolling element bearing fault diagnosis-their effectiveness and flexibilities,” Journal of Vibration and Acoustics, Vol. 123, No. 3, pp. 303–310, Jul. 2001, https://doi.org/10.1115/1.1379745
-
D. F. Shi, W. J. Wang, and L. S. Qu, “Defect detection for bearings using envelope spectra of wavelet transform,” Journal of Vibration and Acoustics, Vol. 126, No. 4, pp. 567–573, Oct. 2004, https://doi.org/10.1115/1.1804995
-
D. Wang, Q. Miao, X. Fan, and H.-Z. Huang, “Rolling element bearing fault detection using an improved combination of hilbert and wavelet transforms,” Journal of Mechanical Science and Technology, Vol. 23, No. 12, pp. 3292–3301, Dec. 2009, https://doi.org/10.1007/s12206-009-0807-4
-
G. F. Bin, J. J. Gao, X. J. Li, and B. S. Dhillon, “Early fault diagnosis of rotating machinery based on wavelet packets-Empirical mode decomposition feature extraction and neural network,” Mechanical Systems and Signal Processing, Vol. 27, pp. 696–711, Feb. 2012, https://doi.org/10.1016/j.ymssp.2011.08.002
-
K. S. Wang and P. S. Heyns, “Application of computed order tracking, Vold-Kalman filtering and EMD in rotating machine vibration,” Mechanical Systems and Signal Processing, Vol. 25, No. 1, pp. 416–430, Jan. 2011, https://doi.org/10.1016/j.ymssp.2010.09.003
-
S. Abbasion, A. Rafsanjani, A. Farshidianfar, and N. Irani, “Rolling element bearings multi-fault classification based on the wavelet denoising and support vector machine,” Mechanical Systems and Signal Processing, Vol. 21, No. 7, pp. 2933–2945, Oct. 2007, https://doi.org/10.1016/j.ymssp.2007.02.003
-
C. Mishra, A. K. Samantaray, and G. Chakraborty, “Rolling element bearing defect diagnosis under variable speed operation through angle synchronous averaging of wavelet de-noised estimate,” Mechanical Systems and Signal Processing, Vol. 72-73, pp. 206–222, May 2016, https://doi.org/10.1016/j.ymssp.2015.10.019
-
N. G. Nikolaou and I. A. Antoniadis, “Rolling element bearing fault diagnosis using wavelet packets,” NDT and E International, Vol. 35, No. 3, pp. 197–205, Apr. 2002, https://doi.org/10.1016/s0963-8695(01)00044-5
-
C. K. Mechefske and J. Mathew, “Fault detection and diagnosis in low speed rolling element bearings part II: the use of nearest neighbour classification,” Mechanical Systems and Signal Processing, Vol. 6, No. 4, pp. 309–316, Jul. 1992, https://doi.org/10.1016/0888-3270(92)90033-f
-
H. Xu, D. He, H. Ma, K. Yu, X. Zhao, and Y. Yang, “A method for calculating radial time-varying stiffness of flexible cylindrical roller bearings with localized defects,” Engineering Failure Analysis, Vol. 128, p. 105590, Oct. 2021, https://doi.org/10.1016/j.engfailanal.2021.105590
-
X. Jin, Y. Chen, L. Wang, H. Han, and P. Chen, “Failure prediction, monitoring and diagnosis methods for slewing bearings of large-scale wind turbine: A review,” Measurement, Vol. 172, p. 108855, Feb. 2021, https://doi.org/10.1016/j.measurement.2020.108855
-
Z. H. Zhang et al., “The assembly method is optimized and applied for For-point contact ball bearing,” Bearing, Dec. 2022.
-
Z. G. Ma et al., “Shock-chain detection method for fault diagnosis of wind turbine pitch bearing,” Mechanical Science and Technology for Aerospace Engineering, Vol. 39, pp. 1426–1431, Jun. 2020, https://doi.org/10.13433/j.cnki.1003-8728.20190284
-
C. Yang et al., “Analysis of load and life of EMU axle box bearing considering wheel polygonization evolution,” Journal of Vibration Engineering, Dec. 2022.
-
L. Quagliato, D. Kim, N. Lee, S. Hwang, J. Domblesky, and N. Kim, “Run-out based crossed roller bearing life prediction by utilization of accelerated testing approach and FE numerical models,” International Journal of Mechanical Sciences, Vol. 130, pp. 99–110, Sep. 2017, https://doi.org/10.1016/j.ijmecsci.2017.06.006
-
N. Jouini, P. Revel, and G. Thoquenne, “Influence of surface integrity on fatigue life of bearing rings finished by precision hard turning and grinding,” Journal of Manufacturing Processes, Vol. 57, pp. 444–451, Sep. 2020, https://doi.org/10.1016/j.jmapro.2020.07.006
-
G. E. Morales-Espejel and A. Gabelli, “A model for rolling bearing life with surface and subsurface survival: surface thermal effects,” Wear, Vol. 460-461, p. 203446, Nov. 2020, https://doi.org/10.1016/j.wear.2020.203446
-
F. Cavacece et al., “Roller bearing under high loaded oscillations: Life evolution and accommodation mechanisms,” Tribology International, Vol. 147, p. 106278, Jul. 2020, https://doi.org/10.1016/j.triboint.2020.106278
-
D. Sandoval, U. Leturiondo, Y. Vidal, and F. Pozo, “Entropy indicators: an approach for low-speed bearing diagnosis,” Sensors, Vol. 21, No. 3, p. 849, Jan. 2021, https://doi.org/10.3390/s21030849
-
D. Sandoval, U. Leturiondo, F. Pozo, and Y. Vidal, “Low-speed bearing fault diagnosis based on permutation and spectral entropy measures,” Applied Sciences, Vol. 10, No. 13, p. 4666, Jul. 2020, https://doi.org/10.3390/app10134666
-
R. Chen, J. Zhu, X. Hu, H. Wu, X. Xu, and X. Han, “Fault diagnosis method of rolling bearing based on multiple classifier ensemble of the weighted and balanced distribution adaptation under limited sample imbalance,” ISA Transactions, Vol. 114, pp. 434–443, Aug. 2021, https://doi.org/10.1016/j.isatra.2020.12.034
-
Y. Dong, Y. Li, H. Zheng, R. Wang, and M. Xu, “A new dynamic model and transfer learning based intelligent fault diagnosis framework for rolling element bearings race faults: solving the small sample problem,” ISA Transactions, Vol. 121, pp. 327–348, Feb. 2022, https://doi.org/10.1016/j.isatra.2021.03.042
-
J. Li, Y. Liu, and Q. Li, “Intelligent fault diagnosis of rolling bearings under imbalanced data conditions using attention-based deep learning method,” Measurement, Vol. 189, p. 110500, Feb. 2022, https://doi.org/10.1016/j.measurement.2021.110500
-
B. Zhao, X. Zhang, Z. Zhan, and Q. Wu, “A robust construction of normalized CNN for online intelligent condition monitoring of rolling bearings considering variable working conditions and sources,” Measurement, Vol. 174, p. 108973, Apr. 2021, https://doi.org/10.1016/j.measurement.2021.108973
-
G. Huang, Y. Zhang, and J. Ou, “Transfer remaining useful life estimation of bearing using depth-wise separable convolution recurrent network,” Measurement, Vol. 176, p. 109090, May 2021, https://doi.org/10.1016/j.measurement.2021.109090
-
Z. Pan, Z. Meng, Z. Chen, W. Gao, and Y. Shi, “A two-stage method based on extreme learning machine for predicting the remaining useful life of rolling-element bearings,” Mechanical Systems and Signal Processing, Vol. 144, p. 106899, Oct. 2020, https://doi.org/10.1016/j.ymssp.2020.106899
-
N. Rezazadeh, A. de Luca, and D. Perfetto, “Unbalanced, cracked, and misaligned rotating machines: a comparison between classification procedures throughout the steady-state operation,” Journal of the Brazilian Society of Mechanical Sciences and Engineering, Vol. 44, No. 10, pp. 1–14, Oct. 2022, https://doi.org/10.1007/s40430-022-03750-1
-
F. Zou et al., “An anti-noise one-dimension convolutional neural network learning model applying on bearing fault diagnosis,” Measurement, Vol. 186, p. 110236, Dec. 2021, https://doi.org/10.1016/j.measurement.2021.110236
-
H. Wang, C. Liu, W. Du, and S. Wang, “Intelligent diagnosis of rotating machinery based on optimized adaptive learning dictionary and 1DCNN,” Applied Sciences, Vol. 11, No. 23, p. 11325, Nov. 2021, https://doi.org/10.3390/app112311325
About this article
This work was supported in part by the National Natural Science Foundation of China (Grant No. 52275138), the Key Research and Development Projects of Henan Province (Grant No. 231111221100, 221111240200), the Science and Technology Major Project of Henan Province of China (Grant No. 221100220200), and the Key science and technology research project of the Henan province (Grant No. 232102221039).
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
Simin Li: writing, doing the experiment, collecting engineering vibration signal. Hongchao wang: programming, ideology.
The authors declare that they have no conflict of interest.

