The structural dimension parameter optimization method of tapered roller bearings for wind power gearbox

Hao, Ruiqin; Li, Yan; Han, Zeguang; Han, Yu

doi:10.21595/vp.2023.23303

Vibroengineering Procedia

Browse Procedia

Published: 18 May 2023

Check for updates

The structural dimension parameter optimization method of tapered roller bearings for wind power gearbox

Ruiqin Hao¹

Yan Li²

Zeguang Han³

Yu Han⁴

^{1, 2, 3}School of Mechanical Engineering, Shenyang Jianzhu University, Shenyang, China

⁴Shanghai Envision Energy Co., Ltd, Shanghai, China

Corresponding Author:

Zeguang Han

Cite the article Download PDF

Downloads 200

Abstract

Taking the non-standardized internal structural dimension parameters of rolling bearings as the design variable, the constrained optimization mathematical model of tapered roller bearings under the maximum target of basic static load rating and basic dynamic load rating has been established. Optimization results of the mathematical model have been obtained by using the improved multi-objective genetic algorithm, NSGA-II. After the above-mentioned methods were used to the optimization of the tapered roller bearing on the high-speed shaft of a 750 kW wind turbine gearbox, its basic rated static load and basic rated dynamic load can be increased by 15 % and 17 % compared with its standard value. Thus, the proposed methods are feasible and reliable, and has certain application value for improving the bearing performance and prolonging its service life.

1. Introduction

Tapered roller bearing is one of the core components of wind power gearbox, and its performance directly affects the working life, safety and stability of the gearbox [1]. Due to the high maintenance cost of wind power equipment, it is of great significance to extend its service life and reduce the maintenance times. Therefore, the research on rolling bearing around wind power equipment has become one of the key fields in recent years. The analysis shows that the performance of the rolling bearing is closely related to the geometric size and shape of each component of the bearing. The change of these parameter values has a great relationship with improving its working performance and extending its service life. Some valuable research results have been obtained by a series of researches. Zhang et al. [2] established a multi-objective optimal design model for cross roller bearings, and obtained the optimal parameters to significantly improve the rated dynamic load of bearings by adopted genetic algorithm. Eugenio [3] proposed an optimization model of tapered roller bearing system with arbitrary combination of radial force and axial force, and obtained the optimal matching among internal structure sizes of bearings under the maximum dynamic load and static load bearing capacity. Rajiv and Jat [4] took spherical roller bearings as the research object, established a three-objective optimization model of maximum dynamic bearing capacity, minimum elastic fluid dynamic oil film thickness and minimum bearing temperature, and obtained the optimal structural parameter values significantly improved bearing life by solving the genetic algorithm. Zhang et al. [5] took four-row tapered roller bearings with large conical angles as the research object, and established a constrained optimization model taking the root thickness of the inner ring guard, the minimum inner diameter of the outer ring and the nominal contact Angle as the design variables, and solved. Yuan et al. [6] took the double-row tapered roller bearing in wind power transmission system as the research object, established the optimization model of minimum volume and maximum life, and obtained satisfactory results. Zhou et al. [7] solved the optimization model of double-row tapered roller bearing with genetic algorithm, analyzed the different crossover rates on the influence of the optimization target value.

From the existing research, the multi-objective optimization of tapered roller bearing is mostly solved by converting the multi-objective optimization model into the single objective optimization model. The optimization results are subject to too much human intervention and cannot fully reflect the advantages of multi-objective optimization. Thus, the main goal of this work is focused on the development of a theoretical model that can be used to study the larger load, longer life and more convenient maintenance tapered roller bearings for wind power gearbox. This paper is organized as follows. Section 2 gives a detailed introduction about the construction method of the optimization model of tapered roller bearing. Section 3 introduces the solution method of the optimization model mentioned above. In Section 4, numerical results for a tapered roller bearings for wind power gearbox are obtained and discussed. Finally, the conclusions are presented in Section 5.

2. The optimization model of tapered roller bearing

2.1. Design variables

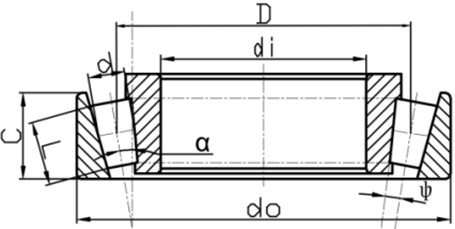
The wind turbine gearboxes are typical helical cylindrical speed incremental drives where the high speed stage shaft is supported by a pair of tapered roller bearings. Feedback from users indicates that the bearings have a short life and therefore need to be optimized to improve their performance. The tapered roller bearing consists of a number of parts, including a series of balls, one cage, the inner and outer raceways, as shown in Fig. 1. The bearing parameters, such as the outer diameter, $d_{0}$ ; the inner diameter, $d_{i}$ , and the bearing width of the bearing, $C$ have formulated strict standards in GB/ T272-2017. The others, such as the mean diameter, $d$ ; the number of rollers, $Z$ ; the effective contact length of roller, $L$ ; the contact Angle, $α$ ; and the half cone Angle, $φ$ etc. are not standardized. Different combination among the values of these parameters will have an important impact on the bearing performance. Thus, the above parameters are selected as design variables. In order to ensure that the optimization parameter values can better meet the actual engineering requirements, the other independent design variables of the optimization model of tapered roller bearing are as follows: control coefficient of rolling body diameter, $K_{D m i n}$ and $K_{D m a x}$ ; width control factor, $β$ ; control coefficient of bearing pitch diameter, $e$ ; and outer ring thickness control factor, $ε$ . Therefore, the independent design variables of the optimal model of tapered roller bearing can be expressed as:

1

X = {[d, D, Z, L, α, φ, K_{D m i n}, K_{D m a x}, β, e, ε]}^{T} .

Fig. 1Structural dimension parameters of tapered roller bearings

2.2. Objective functions

2.2.1. Maximum basic static load rating

The main performance index of tapered roller bearings working at low speed and heavy load is the basic rated static load. The greater the basic rated static load is, the higher the static strength of rolling bearing is. Therefore, in order to improve the working performance of bearings under low speed and heavy load conditions, the larger the basic rated static load of tapered roller bearings $C_{0 r}$ is, the better the carrying capacity is. The corresponding objective function is shown in Eq. (2):

2

M a x f_{1} (X) = 44 [1 - (\frac{d}{D}) c o s α] Z L d c o s α .

2.2.2. Maximum basic rated dynamic load

The basic dynamic load rating is the main determinant of fatigue life of rolling bearings under medium and high-speed operating conditions. The larger the basic dynamic load rating is, the longer the fatigue life of rolling bearing is. The Lundberg-Palmgren formula is used internationally to calculate the basic dynamic load rating. Therefore, the objective function for the basic dynamic load rating of tapered roller bearings $C_{r}$ is expressed as follows:

3

M a x f_{2} (X) = b_{m} f_{c} {(i L c o s α)}^{\frac{7}{9}} Z^{\frac{3}{4}} d^{\frac{29}{27}},

where $i$ is the number of bearing rows, $b_{m}$ is the correction factor, $b_{m}$ = 1.1, $f_{c}$ is a coefficient, expressed as follows:

f_{c} = 172.5 {\{1 + {[1.04 {(\frac{D - d c o s α}{D + d c o s α})}^{14 / 108}]}^{9 / 2}\}}^{- 2 / 9} \frac{{(\frac{d c o s α}{D})}^{2 / 9} {(1 - \frac{d c o s α}{D})}^{29 / 27}}{{(1 + \frac{d c o s α}{D})}^{1 / 4}} .

2.3. Constraint conditions

Tapered roller bearing is composed of inner ring, outer ring, tapered roller and cage that their geometric sizes are interrelated. Therefore, the design variables of the optimization model must meet some regulations and requirements, which constitute the constraints of the optimization model.

2.3.1. Constraints on the mean diameter of rollers

In order to ensure the reasonable assembly of bearings, the average diameter of rollers must be limited within a certain range by the inner and outer diameters of bearings. Here, it is limited by $K_{D m a x}$ and $K_{D m i n}$ . The corresponding constraint conditions can be expressed as follows:

4

g_{1} (X) = \frac{K_{D m i n} (d_{0} - d_{i})}{2 c o s α} - d \leq 0,

5

g_{2} (X) = d - \frac{K_{D m a x} (d_{0} - d_{i})}{2 c o s α} \leq 0 .

2.3.2. Constraints on pitch diameter of bearings

In order to ensure the good operation of rollers in bearings, the pitch diameter of bearings, which is expressed by $e$ , should not be too different from its average diameter. The constraint conditions are written as:

6

g_{3} (X) = (0.5 - e) (d_{0} + d_{i}) - D \leq 0,

7

g_{4} (X) = D - (0.5 + e) (d_{0} + d_{i}) \leq 0 .

2.3.3. Constraints on the effective contact length of rollers

The effective contact length of rollers is limited by the bearing width. After introducing the bearing width control parameter $β$ , the constraint condition can be expressed as:

8

g_{5} (X) = L - \frac{β C}{c o s α} \leq 0 .

In order to ensure the bearing capacity of tapered roller bearings, $L$ should not be less than $d$ , the constraint condition can be expressed as:

9

g_{6} (X) = d - L \leq 0 .

2.3.4. Constraints on the number of rollers

The more rollers there are, the greater the bearing capacity. But the number of rollers $Z$ is limited by the bearing assembly space. The constraint condition which ensure that rollers can be smoothly assembled between inner and outer rings can be expressed as:

10

g_{7} (X) = Z - \frac{π D}{(d + L s i n φ)} \leq 0 .

2.3.5. Constraints on raceway thickness of bearing outer ring

According to the standard, the thickness of the bottom of the outer ring of the bearing should be greater than or equal to $ε d$ .Thus, the constraint equation of the bottom thickness of the outer ring is derived as follows:

11

g_{8} (X) = ε d - \frac{0.5 (d_{0} - d - D)}{c o s α} \leq 0 .

2.3.6. Constraints on roller spacing

In order to avoid collision between rollers, there must be a certain gap between two adjacent rollers, so the constraint condition can be expressed as:

12

g_{9} (X) = Z {s i n}^{- 1} (\frac{d c o s α}{D}) + \frac{π Z}{360} - π \leq 0 .

2.4. Optimization algorithm selection

As previously mentioned, the optimization model is a nonlinear constrained optimal model with two objective functions and nine constraints. In order to avoid the disadvantages which have to take derivative of the functions and is difficult to obtain global optimal solutions using the conventional optimal algorithm, a fast non-dominated sorting algorithm, NSGA-II is selected as the solution algorithm.

2.5. Engineering example

2.5.1. Design conditions

The bearing (32222) used in the high speed shaft of 750 kW wind power gearbox is chosen as an example to demonstrate the application of the methodologies presented in this paper. Using bearing geometry and performance data obtained by checking the standards are as follows: the outer diameter is $d_{0}$ = 200 mm, the inner diameter is $d_{i}$ = 110 mm, the width is $C$ = 46 mm, the number of columns is $i$ = 1, the basic rated dynamic load is $C_{r}$ = 343830 N, the basic rated static load is $C_{o r}$ = 524650 N. The radial load borne by the bearing is $F_{r}$ = 13215 N, and the axial load borne by the bearing is $F_{a}$ = 18820 N.

2.5.2. Range of values for design variables

The literature [8] gives the value range of design variables as follows: $K_{D m i n} \in$ [0.3, 0.4], $K_{D m a x} \in$ [0.5, 0.6], $e \in$ [0.01, 0.07], $β \in$ [0.7, 0.85], $ε \in$ [0.4, 0.5]. The value ranges of other design variables determined by structural analysis are: $d \in$ [15, 30], $Z \in$ [15, 25], $L \in$ [30, 38], $α \in$ [10, 30], $φ \in$ [1, 10], $D \in$ [148, 157].

2.5.3. Optimization results

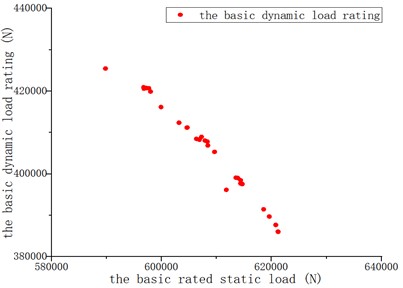
According to the previous experience using NSGA-II optimization algorithm and the needs of this optimization design, the relevant parameters required by the algorithm are selected as follows: the number of population is 100, the maximum number of generations is 500, the crossover probability is 0.8, the mutation probability is 0.08, the cross distribution index is 1, the mutation distribution index is 1, and the random seed is 0.5. Fig. 2 shows the 100 Pareto solutions that satisfy this requirement.

After data analysis and rule combination of the above 100 Pareto solutions, 14 groups of excellent and practical multi-objective Paretosolutions are obtained, as shown in Table 1. (The method of analysis and rule combination has been omitted due to space constraints.)

Table 1Multi-objective Pareto solution of tapered roller bearing

No.	Design variables and target values
No.	$d$ (mm)	$Z$ (–)	$L$ (mm)	$α$ (°)	$Φ$ (°)	$D$ (mm)	$K_{D m i n}$ (–)	$K_{D m a x}$ (–)	$e$ (–)	$β$ (–)	$ε$ (–)	$C_{o r}$ (N)	$C_{r}$ (N)
1	18.83	22	38	10.49	1.38	156.99	0.347	0.596	0.064	0.842	0.401	600740	376480
2	23.28	18	38	12.63	1.07	156.95	0.353	0.590	0.065	0.848	0.412	584730	412840
3	21.24	20	38	10	1.25	156.93	0.304	0.590	0.065	0.831	0.413	606240	404850
4	21.22	20	38	13.16	1.09	156.84	0.314	0.590	0.065	0.830	0.425	599930	400440
5	24.26	17	38	11.45	1.20	156.35	0.328	0.588	0.065	0.839	0.407	573060	416280
6	20.21	21	38	10.01	1.40	156.97	0.356	0.596	0.068	0.830	0.421	610210	396060
7	18.83	22	38	10.49	1.18	156.96	0.323	0.596	0.063	0.842	0.401	600730	376490
8	21.22	20	38	13.58	1.16	156.85	0.314	0.596	0.065	0.832	0.404	599050	399820
9	18.83	22	38	10.49	1.00	156.96	0.305	0.596	0.061	0.825	0.422	600730	376490
10	24.26	17	38	11.45	1.20	156.22	0.342	0.594	0.065	0.847	0.407	572980	416300
11	18.83	22	38	10.49	1.20	156.99	0.304	0.596	0.063	0.832	0.401	600740	376480
12	20.22	21	38	10.00	1.09	156.91	0.340	0.591	0.067	0.840	0.435	610450	396310
13	18.82	22	38	10.49	1.15	156.97	0.325	0.596	0.057	0.837	0.422	600460	376250
14	21.23	20	38	10.00	1.06	156.93	0.304	0.590	0.065	0.831	0.413	606000	404630

Compared with the standard values, it can be observed that the basic rated static load and basic rated dynamic load of the bearing in Table 1 are at least 15 % and 17 % higher than the standard values.

Fig. 2100 Pareto solutions

3. Conclusions

A general methodology for modelling and simulation of tapered roller bearings using in wind power gearbox was presented and discussed throughout this work. The tapered roller bearings used is modeled by introducing multi-function nonlinear optimization model, with two objectives, one is to maximize the basic dynamic load rating, and the other is to maximize the basic static load rating. Simultaneously, the above model contains nine constraints, which takes into account the pitch diameter of bearings, the effective contact length of rollers, the number of rollers, the raceway thickness of bearing outer ring, and the roller spacing. The solution method of the model is based on NSGA-II. The tapered roller bearings (32222) was used as a numerical example application.

From the results obtained, several feasible optimization schemes were easily obtained. Compared with the standard bearings in use, under the premise that the standard values such as inner diameter, outer diameter and width remained unchanged, the basic rated static load and basic rated dynamic load of post-optimality bearings are increased by at least 15 % and 17 % respectively. It is obvious that the bearing life is extended to a certain extent, the optimization method is feasible and reliable, and can provide effective support for the design and manufacture of wind power gearbox bearings.

The software of tapered roller bearing optimization for wind power equipment has been developed successfully. It can provide a guarantee for the rapid and efficient acquisition of multiple bearing schemes, provide an effective support for the rich bearing product series, high-performance bearing design and manufacturing, and provide a guarantee for meeting the diversified needs of customers.

References

J. M. Xie, B. H. Yu, and C. L. Zong, “Application of improved particle swarm optimization in tapered roller bearing,” Bearing, No. 9, pp. 4–7, 2009, https://doi.org/10.19533/j.issn1000-3762.2009.09.002

Publisher
G. Zhang, J. Ruan, Q. Z. Yin, X. Zhang, D. D. Jiang, and Y. Liu, “Optimum design of crossed roller bearings based on genetic algorithms,” Bearing, No. 12, pp. 1–3, 2010, https://doi.org/10.19533/j.issn1000-3762.2010.12.001

Publisher
E. Dragoni, “Optimal design of tapered roller bearings for maximum rating life under combined loads,” Mechanics and Industry, Vol. 18, No. 1, p. 112, 2017, https://doi.org/10.1051/meca/2016025

Publisher
R. Tiwari and A. Jat, “Optimal design of spherical roller bearings based on multiple tasking operating requirements,” Multidiscipline Modeling in Materials and Structures, Vol. 16, No. 5, pp. 967–990, Aug. 2020, https://doi.org/10.1108/mmms-07-2019-0129

Publisher
T. Zhang, L. Zhao, and C. Y. Mu, “Research on optimization design method of four-row tapered roller bearing with large conical angle (in Chinese),” (in Chinese), Electronic World, No. 19, pp. 19–20, 2018, https://doi.org/10.19353/j.cnki.dzsj.2018.19.006

Publisher
H. L. Yuan, J. Qiu, Z. Wang, and D. L. Wang, “Multi-objective optimation design of bearing in wind power transmission system,” Machine Design and Manufacturing Engineering, Vol. 49, No. 10, pp. 21–26, 2020.

Search CrossRef
Y. P. Zhou, F. H. Mao, and J. Qiu, “Research on optimal design method of double-row tapered roller bearing,” Machinery Design and Manufacture, No. 8, pp. 17–20, 2021, https://doi.org/10.19356/j.cnki.1001-3997.2021.08.005

Publisher
R. Tiwari, K. K. Sunil, and R. S. Reddy, “An optimal design methodology of tapered roller bearings using genetic algorithms,” International Journal for Computational Methods in Engineering Science and Mechanics, Vol. 13, No. 2, pp. 108–127, Mar. 2012, https://doi.org/10.1080/15502287.2011.654375

Publisher

About this article

Received

03 April 2023

Accepted

24 April 2023

Published

18 May 2023

SUBJECTS

System dynamics in manufacturing system modeling

DOI

https://doi.org/10.21595/vp.2023.23303

Keywords

multi-objective optimization design

NSGA-II

tapered roller bearing

Acknowledgements

The authors have not disclosed any funding.

Data Availability

The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

Conflict of interest

The authors declare that they have no conflict of interest.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2019 09 30

An optimized bearing parameter identification approach from vibration response spectra

Rajasekhara Reddy Mutra, Srinivas J

Research article

2018 10 19

Multi-objective rotor dynamics optimization of the plain bearing-rotor system

Xi Kuang, Gui-huo Luo, Fei Wang

Research article

2018 06 30

PI-tuned UPFC damping controllers design for multi-machine power system

G. Kannayeram, P. S. Manoharan, N. B. Prakash

Research article

2017 02 15

Surrogate-based multi-objective optimization of firing accuracy and firing stability for a towed artillery

Hui Xiao, Guolai Yang, Jianli Ge

R. Hao, Y. Li, Z. Han, and Y. Han, “The structural dimension parameter optimization method of tapered roller bearings for wind power gearbox,” Vibroengineering PROCEDIA, Vol. 49, pp. 239–245, May 2023, https://doi.org/10.21595/vp.2023.23303

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/vp.2023.23303
UR  - https://doi.org/10.21595/vp.2023.23303
TI  - The structural dimension parameter optimization method of tapered roller bearings for wind power gearbox
T2  - Vibroengineering PROCEDIA
AU  - Hao, Ruiqin
AU  - Li, Yan
AU  - Han, Zeguang
AU  - Han, Yu
PY  - 2023
DA  - 2023/05/18
PB  - JVE International Ltd.
SP  - 239-245
VL  - 49
SN  - 2345-0533
SN  - 2538-8479
ER  - 

Copy Ris

Copied to clipboard!

@article{Hao_2023,
	doi = {10.21595/vp.2023.23303},
	url = {https://doi.org/10.21595/vp.2023.23303},
	year = 2023,
	month = {may},
	publisher = {{JVE} International Ltd.},
	volume = {49},
	pages = {239--245},
	author = {Ruiqin Hao and Yan Li and Zeguang Han and Yu Han},
	title = {The structural dimension parameter optimization method of tapered roller bearings for wind power gearbox},
	journal = {Vibroengineering {PROCEDIA}}
}

Copy Bibtex

Copied to clipboard!

[1]R. Hao, Y. Li, Z. Han, and Y. Han, “The structural dimension parameter optimization method of tapered roller bearings for wind power gearbox,” Vibroengineering PROCEDIA, vol. 49, pp. 239–245, May 2023, doi: 10.21595/vp.2023.23303.

Copy IEEE

Copied to clipboard!

Hao, Ruiqin, Yan Li, Zeguang Han, and Yu Han. “The Structural Dimension Parameter Optimization Method of Tapered Roller Bearings for Wind Power Gearbox.” Vibroengineering PROCEDIA 49 (May 18, 2023): 239–45. https://doi.org/10.21595/vp.2023.23303.

Copy Chicago

Copied to clipboard!

The structural dimension parameter optimization method of tapered roller bearings for wind power gearbox

Abstract

1. Introduction

2. The optimization model of tapered roller bearing

2.1. Design variables

2.2. Objective functions

2.2.1. Maximum basic static load rating

2.2.2. Maximum basic rated dynamic load

2.3. Constraint conditions

2.3.1. Constraints on the mean diameter of rollers

2.3.2. Constraints on pitch diameter of bearings

2.3.3. Constraints on the effective contact length of rollers

2.3.4. Constraints on the number of rollers

2.3.5. Constraints on raceway thickness of bearing outer ring

2.3.6. Constraints on roller spacing

2.4. Optimization algorithm selection

2.5. Engineering example

2.5.1. Design conditions

2.5.2. Range of values for design variables

2.5.3. Optimization results

3. Conclusions

References

About this article

Related Articles