Abstract
A three-dimensional numerical model of the tank’s barrel was established using the finite element method, and dynamic process of thermal load boundary changing with projectile movement was defined. The evolution of the temperature distribution of the barrel under the firing conditions of the first projectile was obtained through numerical calculations. Furthermore, a multi-body dynamics software was used to build a shooting model for tank with a temperature field, the effects of the temperature field on the vibration of the barrel and the attitude of the projectile were studied and calculated, finally, the regular pattern of the stress of the barrel under the temperature field was analyzed. The simulation results of this model show that temperature field has a negligible effect on the barrel vibration and the projectile attitude.
Highlights
- Dynamic process of thermal load boundary changing with projectile movement was defined.
- The evolution of the temperature distribution of the barrel under the firing conditions of the first projectile was obtained.
- A multi-body dynamics software was used to build a shooting model for tank with a temperature field.
- Temperature field has a negligible effect on the barrel vibration and the projectile attitude.
1. Introduction
When the tank is shooting on the move, the inner wall of the tank barrel is continuously heated by the transient thermal pulse of the gunpowder combustion, which means that the temperature of the barrel rising rapidly, and the temperature of the inner wall of the barrel is significantly higher than other parts. The high temperature is not only the primary factor for barrel ablation, but also changes dynamic characteristics of the barrel, which causes the vibration during firing, and affects the attitude of the projectile out of the muzzle [1].
Therefore, when we calculate the shooting problem during tank’s travelling, the temperature field becomes a factor that cannot be ignored. In this paper, a multi-body dynamics software is used to build a shooting model of a tank with a temperature field, and the temperature distribution of the barrel during the shooting process can be obtained. In this study we not only have a clearer understanding of the process of temperature propagation of the barrel, but also more importantly study the effect of the temperature field on the attitude of the projectile's muzzle when the tank is firing during travel. This has reference value for improving the firing accuracy of tank artillery.
2. Mathematical model of chamber temperature
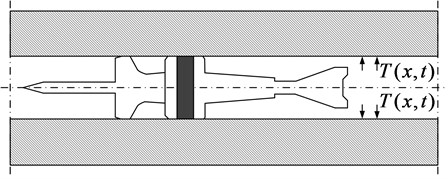
In the inner-ballistic period,the space behind the bomb is the area where the gunpowder and gas work, the dynamic response of the barrel is mainly determined by the effect of high-temperature gunpowder gas. Heat convection between the high temperature effect in the chamber and the inner wall, then, a certain temperature difference stress is generated. Fig. 1 is the dynamic effect of gunpowder gas, x is the corresponding thermal shock load at time, t is the time increment. The space behind the projectile gradually expands as the projectile moves axially, that is, the area of action depends on the position of the projectile.
2.1. Mathematical model of temperature field
The firing process is accompanied by complex thermal field changes, thermal convection between the high-temperature gunpowder gas and the inner wall of the barrel causes the temperature rising rapidly. During firing, the heat transfer in the inner chamber is conducted in three ways: conduction, convection and radiation. Pointed out that radiative heat transfer is about 1 % of convective heat transfer, so the effect of heat radiation is ignored. The physical model of the barrel’s temperature field can be expressed as:
1) The convective heat exchange between the high temperature gas and the inner chamber belongs to the transient temperature field [2]. The differential equation of heat transfer in the chamber in three-dimensional is:
where ρ is density, cT is specific heat capacity, T is temperature, Q is intensity of heat source, kx, ky, kz are thermal conductivity in three axes respectively.
2) Convection heat transfer between barrel surface and gunpowder gas, under the influence of external environmental factors, in this case, a third thermal boundary condition is used for description.
Fig. 1Follow-up process of gas loading boundary
The inner boundary condition is:
the outer boundary condition is:
where nx, ny, nz are the normal direction cosine outside the border respectively, hi, ho are the internal and external convective heat transfer coefficient respectively, Tg is gunpowder gas temperature, T∞ is ambient temperature.
When we use the finite element method to solve differential equation, the temperature in the spatial discrete domain can be obtained by interpolation of the node temperature, which means that:
where Ni is the shape function of nodes, T is the node temperature. The finite element equation of the discrete transient temperature field is:
where KT is the stiffness matrix of temperature, CT is the matrix of instantaneous temperature changes; PT is the heat load vector of nodes.
3. Kinetic modeling
As an example, a 125 mm tank gun is modeled by multi-body dynamics software RecurDyn, corresponding thermal loads and boundary conditions are applied, further, the dynamic response of the barrel and projectile during the shooting process of the tank is simulated. The numerical model is based on the following basic assumptions:
1) At any time, the parameters of the gunpowder gas after projectile are equal at any cross section, its unevenness of three-dimensional spatial distribution is ignored, and unburned powder particles are evenly distributed behind the projectile.
2) During the first shot, the surface temperature of the inner barrel is the initial room temperature, the powder gas pressure was set to 30 MPa [3].
3.1. Modeling of tank components
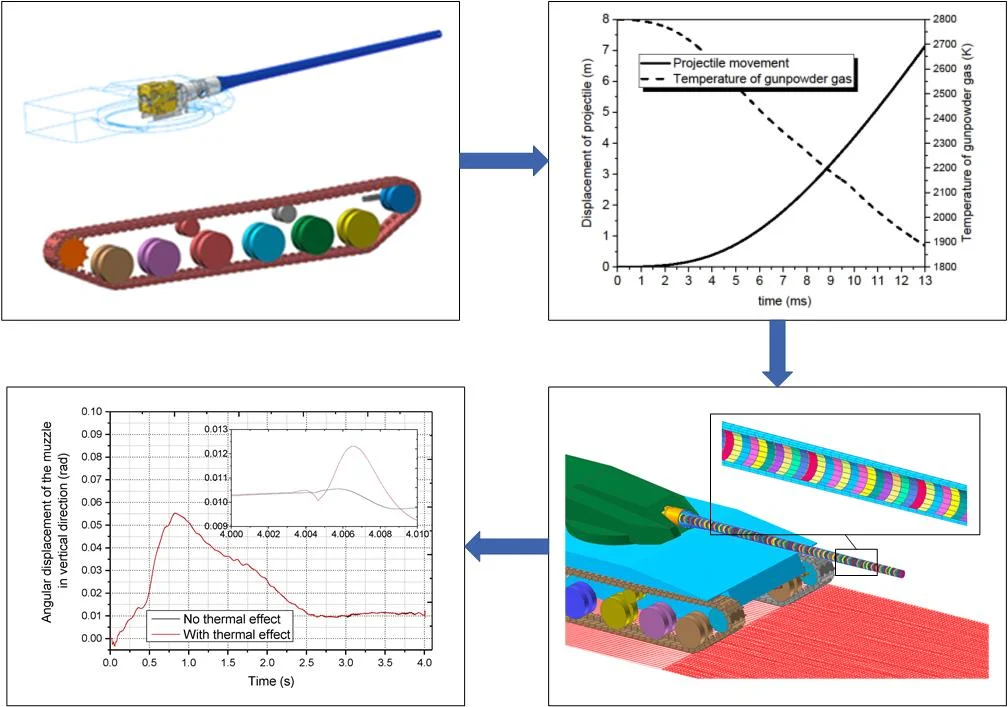
Considering the complex structure of the components in the tank system, it is difficult to perform accurate 3D modeling directly in multi-body dynamics software, therefore, in the modeling of this paper, the rigid body components other than the track are selected to be modeled in CAD software, which are imported into RecurDyn through the software interface. The positional relationship of rigid components needs to be adjusted according to the topology, components are assigned corresponding material properties. The dynamic model of the tank firepower is shown in Fig. 2. Except for the recoil part and the cradle, the mass and moment of inertia of remaining components, secondary components involved in slewing motion, are equivalent to the turret.
Fig. 2Dynamic model of firepower

The tracked chassis is used to reduce running resistance and ensure the high possibility of the tank on soft ground. However, the track device has many complicated components and structure, which has become a difficult problem in the dynamic modeling process. Toolkit > Track module is a professional track modeling module provided in RecurDyn software, which adopts a modular modeling method and can easily establish and modify three-dimensional solid models of road wheels, tug wheels, induction wheels, driving wheels and track shoes by calling component modules in the database. According to the actual size of each component of the track device, the model of the track on one side is shown in Fig. 3.
Fig. 3Tank track model

In the current research on firing dynamics of artillery, the effect of the flexibility of the barrel on the muzzle vibration is taken into account. Modal reduction method is a modeling method to deal with flexible body components, which is commonly used in the research of artillery rigid-flexible coupling, the elasticity of the component is expressed by the mode obtained by the finite element calculation. In this paper, the F-Flex method is selected for flexible barrel modeling. Firstly, the finite element of the barrel is discretized in the finite element software Hypermesh, and the finite element model of the barrel is established. Then saving the divided mesh as an input file (.bdf) in Nastran format. A finite element flexible body model of the barrel is generated by reading the .bdf file in RecurDyn, the flexible barrel is connected to the rigid breech through a rigid node. The finite element model of the barrel is shown in the Fig. 4.
Fig. 4The finite element model of the barrel

3.2. Application of temperature field in the barrel
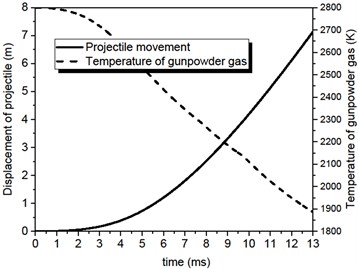
The time-varying curve of gunpowder gas temperature and projectile displacement obtained by solving the classic internal ballistic equation is shown in Fig. 5. It can be seen from the time-varying temperature curve that the starting point corresponds to the explosive temperature of the gunpowder combustion, and then the temperature gradually decreases with the increase of the kinetic energy of the projectile [4].
Fig. 5Time-varying curve of kinetic parameter
Gunpowder gas is an unstable turbulent flow in the barrel. Through forced convection heat transfer, high-temperature gunpowder gas passes through the thermal boundary layer to transfer heat to the barrel. This transient physical process can be defined using the contact boundary film module in Abaqus software.
Fig. 6The final bore temperature application
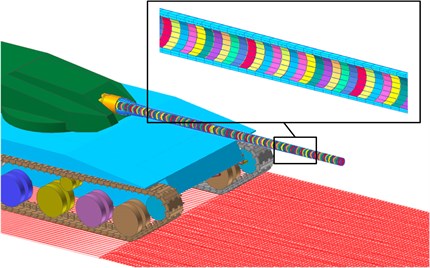
The temperature change of each grid node after the inner wall of the barrel calculated by the finite element software is extracted, and the spline curve is applied to the corresponding grid point position of the flexible barrel in the multibody dynamics software RecurDyn. A judgment statement is used to determine whether the projectile has passed the temperature application grid point. The final bore temperature application results are shown in Fig. 6.
3.3. Modeling of rigid-flexible coupling of projectile
When the tank fires, the projectile moves along the barrel in a predetermined direction. Due to the gap between the barrel and projectile, contact with the inner wall of the barrel will continue to occur during the movement of the projectile bore. In the process of contact and collision, in addition to the normal contact force in the contact area, it is also subject to tangential friction. The tangential contact characteristics of the projectile rigid-flexible coupling model can be described by the friction model.
At present, the most widely used friction model is the Coulomb friction model. The friction force FT is considered to be proportional to the normal contact force FN, which means that:
where μd is the coefficient of sliding friction.
There is a certain gap between the description of friction and the actual situation based on the Coulomb friction model. In order to solve the friction state transition problem when the tangential velocity is zero during the contact collision process, we calculate the tangential friction force based on the following two formulas:
where Fmax is the maximum friction, μ(vt) is the coefficient of friction. The friction coefficient is related to the relative speed, which depends on the static threshold speed vs, dynamic threshold speed vd, coefficient of static friction μs and coefficient of dynamic friction μd. The coefficient of friction corresponding to the relative speed can be determined according to the half-sine step function HAVSIN, which can be calculated by the following formula:
4. Kinetic response under the thermal load
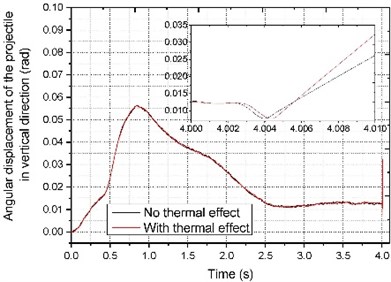
The dynamic response combined thermal effect of the muzzle and projectile calculated based on the multi-body dynamics are shown in Figs. 7-8, the influences of road surface and thermal on barrel are mainly reflected in the vertical direction. The projectile was launched at 4 s. It can be seen that under the action of thermal load, there have been large fluctuations on the vertical displacement of the muzzle, and the posture of the projectile also changed greatly.
Fig. 7Angular displacement of the muzzle in vertical direction
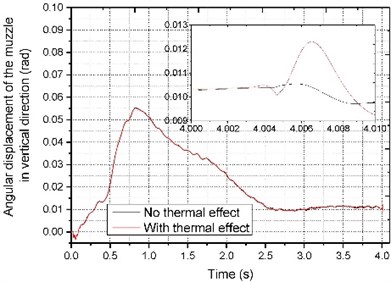
Fig. 8Angular displacement of the projectile in vertical direction
5. Conclusions
When the projectile is fired, part of the energy generated by the explosive detonation of the gunpowder will be converted into the kinetic energy, which propels the projectile forward, so that the projectile will obtain a faster launch speed; The other part of the energy will be converted into heat energy, which is transferred to the barrel through heat transfer methods such as convection and radiation, causing the temperature of the artillery body to increase. Under the action of gunpowder gas, the gun barrel will withstand a large thermal shock in an instant. The temperature rises and falls of the gun barrel wall are completed in a very short time, which will cause changes in the dynamic response of barrel and projectile.
References
-
Wasfy T. M., Noor A. K. Computational strategies for flexible multibody systems. Applied Mechanics Reviews, Vol. 56, Issue 6, 2003, p. 553-613.
-
Li T., Wang Y. Deployment dynamic analysis of deployable antennas considering thermal effect. Aerospace Science and Technology, Vol. 13, Issues 4-5, 2009, p. 210-215.
-
Wu J., Zhao Z. H., Ren G. X. Dynamic analysis of space structure deployment with transient thermal load. Advanced Materials Research, Vol. 479, 2012, p. 803-807.
-
Liu J. Y., Lu H. Thermal effect on the deformation of a flexible beam with large kinematical driven overall motions. European Journal of Mechanics-A/Solids, Vol. 26, Issue 1, 2007, p. 137-151.
