Particle migration in shale oil development

1. Introduction

Shale oil is one of the important research directions for solving oil problems in today’s society. The world’s shale oil resources are rich and far greater than the world’s proven reserves of crude oil. The production of shale oil began in the Western European countries in the 19th century. After the decline of mining, it was once again paid attention to by the world oil crisis.

In recent years, with the deepening of scientific research, people have continuously increased their understanding of particle migration, and scientists have conducted a lot of detailed research in related fields. In 2000, Allende M. and Kalyon D. M. studied the numerical calculation results and simple experimental methods of the particle migration effect of the concentration gradient of particles moving from a high-speed region to a low-speed region when characterizing a non-uniform fluid [1]. In 2005, Makino M.; Doi M. studied the relationship between the average migration velocity of particles in the direction of vorticity and the shear rate, length, and pitch of the particles [2]. In 2010, Min Kyung Hoon and Kim Chongyoup used the diffusion flux model to study the migration of particles in free surface flow. The results show that, although the velocity profile is fully expanded and tended in the plane jet and slit coating flow Yu flat, but the particle distribution in both cases did not reach a uniform distribution [3]. In 2015, Li Gaojin et al. used numerical methods to study the motion of spheres in the channel flow driven by the pressure of viscoelastic fluid. It was found that due to the oscillation of the fluid velocity and the strong normal stress difference generated during the flow start, the particles have a larger transient migration speed, which may be used to accelerate the particle focusing [4]. In 2020, Tai, Cheng-Wei and others made relevant studies on the movement laws of particles of different shapes in fluids.

2. Environmental analysis

The production of shale oil relies mainly on the generation of complex fracture networks around the main fractures. Its flow characteristics are very difficult to predict relative to the production capacity of different fracture networks. The law of liquid flow in these channels still needs in-depth study. Especially for the particles in the channels, their migration will directly lead to the unclogging and clogging of cracks, and it is found that their movement law has a huge effect on the shale oil production.

The migration of particles in shale oil is the migration of particles belonging to the flow of porous media. The fluid flow through the channel is very complicated, and a simple assumption is made here that the fluid flows through a smooth uniform diameter channel. The migration of particles in porous media refers to the process of particles detaching from the surface and following the fluid movement, and remaining in narrow pores or being discharged from the medium when encountering different conditions. In the process of particles detaching from the surface, if the adhesion force or torque applied to the particles is greater than the separation force or torque, then the particles will remain in the attached state, otherwise the particles will fall off the surface.

Fig. 1Schematic diagram of the force of particles in the pores

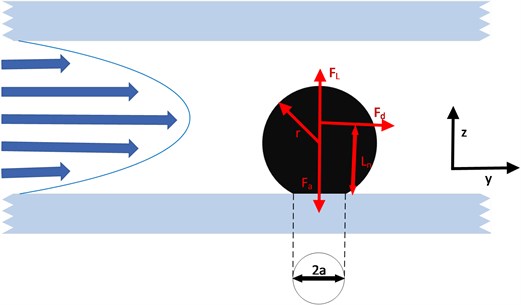
In order to explain the main way of particle detachment, the main force of the single particle acting on the fracture surface is analyzed, as shown in Fig. 1, that is, the force that helps the particle detach, the resistance $F_d$ caused by the pressure gradient of the fluid flow, and the fluid velocity gradient from perpendicular to the surface The lifting force $F_l$, and the force that prevents the particles from separating, the binding force $F_a$ due to physicochemical action, and the friction force $F_f$ generated between the particles and the surface. There is also gravity, but when the particle radius is < 500 µm, gravity is very weak compared to other forces and can be ignored. Similarly, the effect of the horizontal angle of the channel on the particles is not considered.

There are three ways for the particles to initially detach from the surface of the channel: rolling detachment, horizontal detachment, and vertical detachment. Rolling detachment occurs when the torque provided by the fluid exceeds the motion resistance, and horizontal detachment and vertical detachment occur when the resistance of the fluid is greater than the resistance in the tangential or normal direction of the particles, respectively. Rolling off is the main way of particles detaching from the surface of the channel

It follows from this that the boundary conditions for particle separation and the separation force are equal to the force at which the particles are bound to the surface:

where $F_d$ is the resistance to the particles adhering to the surface of the channel, $L_n$ is the lever arm of the force in the horizontal direction, $F_n$ is the total force received by the particles in the vertical direction, and $F_l$ is the lift of the fluid velocity gradient straight to the surface.

According to the previous theoretical model, the following calculations can be made:

The contact radius can be estimated using JKR theory, the formula is as follows:

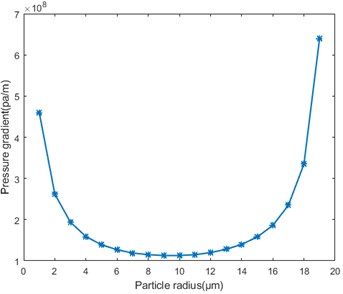
where $K_2$ is the contact elastic modulus. And from this, the trend of particles with pressure changes are shown in Fig. 2.

Fig. 2Pressure conditions with different scale particle size migration

3. Model simulation

In this paper, fluent is used to simulate the state change of the fluid in the pores. First, use the mapping software to draw the model, load it with Ansys, and then generate the grid. Then enter fluent to set the boundary conditions. After setting the step size and the number of steps, initialize and calculate to get the following results.

Fig. 3Fluid velocity simulation under the action of particles

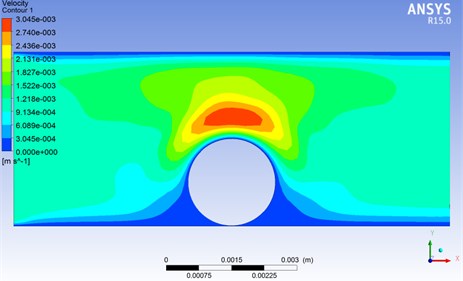
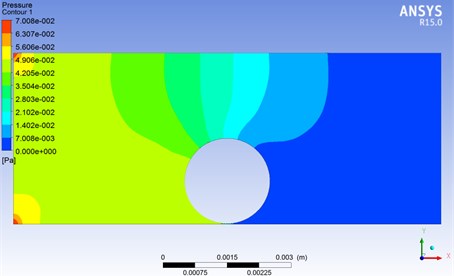
Fig. 4Fluid pressure simulation under the action of particles

As shown in Fig. 3, when the fluid flows through the pores with particles, the flow velocity suddenly increases above the particles, and then decreases rapidly after flowing through the particles.

As shown in Fig. 4, the pressure of the fluid gradually decreases as it flows through the particles, showing a decreasing trend. No more changes after passing through the particles.

4. Experimental arguments

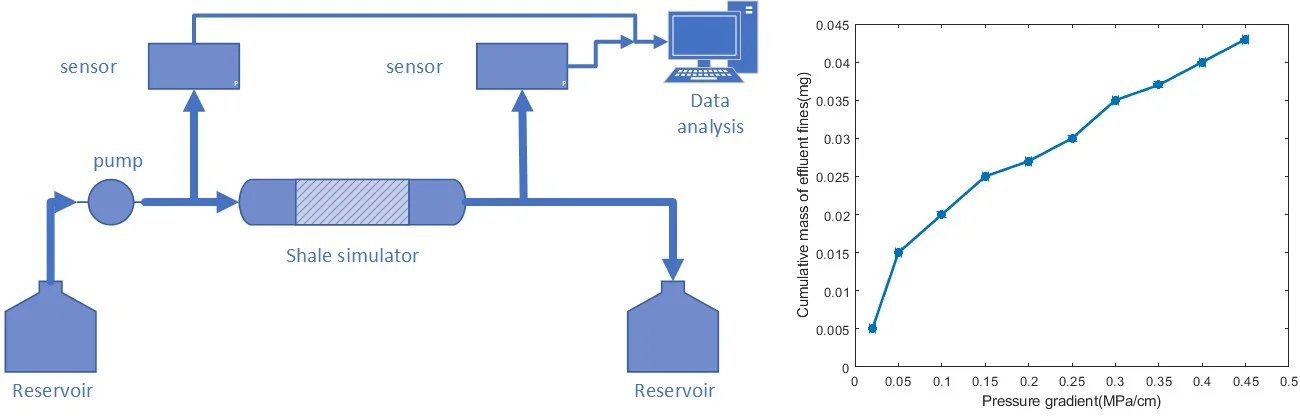
As shown in Fig. 5, the steady-state flow experiment was conducted. The experimental equipment was mainly composed of two reservoirs, a syringe pump, two pressure sensors, a shale simulation device, and a data acquisition system. A syringe pump is used to inject fluid through the shale simulation device at a constant pressure. The reservoir on the right continuously collects the outflow liquid and records the outflow volume of the fluid. Pressure sensors on both sides monitor the pressure at the inlet and outlet of the fluid sample, respectively. The initial outlet pressure is maintained at atmospheric pressure. The pressure on both sides is digitized and transmitted to the data analysis office and the data is recorded in real time.

Fig. 5Experimental schematic

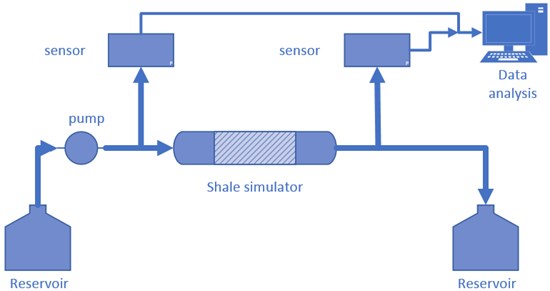
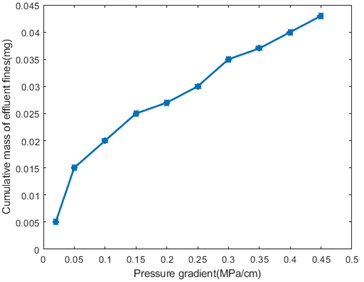
Fig. 6 is a graph of experimental data, where the abscissa is the pressure difference applied across the simulator, and the ordinate is the concentration of particles off the surface. It can be seen from Fig. 6 that as the fluid pressure rises, the particles keep escaping from the surface. It can be seen that the minimum fluid pressure of different particles off the surface is different. From this we can estimate the appropriate production pressure during crude oil extraction.

Fig. 6Experimental data

5. Conclusions

Different particle sizes require different fluid pressures to cause migration, where the required pressure decreases first and then increases as the particle size increases. With the increase of pressure, the range of the size of particles that can migrate increases continuously, and experiments also show that the outflow particles increase with the increase of pressure, which confirms the theoretical calculation. From this we can estimate the appropriate production pressure during crude oil extraction.