Dynamic stiffness method for free vibration analysis of thin functionally graded rectangular plates

1. Introduction

The concept of functionally graded materials was first time introduced by Yamanoushi et.al [1] in 1980 during the advancement of thermal resistance material for aerospace engineering applications. Functionally graded materials are known as a new class of composite materials, which is a mixture of ceramics and metal constituents. The ceramic constituents give high-temperature resistance, whereas metal constituents enhance the mechanical performance and decrease the failure possibility of the structure. Leissa [2] used the Ritz method to analyze free vibration behaviour of the rectangular isotropic plate under applied twenty-one possible boundary conditions. Bercin [3] analyze free vibration and mode shape of the orthotropic plate by using finite element method. Bercin and Langley [4] continued to this work to develop the dynamic stiffness matrix for vibration analysis of plate structures. Boscolo and Banerjee [5] used DSM for analysis of free transverse vibration of the rectangular isotropic plate by using classical plate theory and first-order shear deformation theory. Chauhan et al. [6] used classical plate theory to analyze the free vibration of isotropic plate for different boundaries by using DSM Shen and Yang [7] applied CPT to investigate free vibration behavior of initially stressed elastically founded functionally graded material (FGM) plates under impetuous lateral loading. Baferani et al. [8] used Navier and Levy type solution for the free vibration analysis of functionally graded plate under different boundary conditions by using CPT. Kumar et al. [9] used CPT to formulate the DSM with Wittrick-Williams algorithm to extarct the eigen value of the FGM plates.

In this paper, we have analyzed the free vibration behavior of functionally graded material plates by using dynamic stiffness method with Wittrick-Williams algorithm to extract the natural frequencies under different boundary conditions.

2. Governing differential equation of the functionally graded material plate

Fig. 1. shows a rectangular functionally graded plate of length a, width b and thickness $h$, where material properties vary along with the thickness as a power-law distribution [9] as given by Eq. (1):

where $V_c$ and $V_m$ denotes the volume fractions of ceramics and metal constituents, $k$ represent the power-law index that takes a positive real number in Eq. (1).

Fig. 1Material geometry and coordinates system of the functionally graded plate

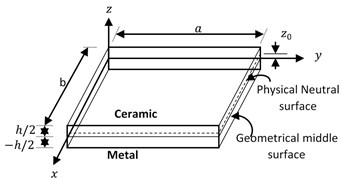
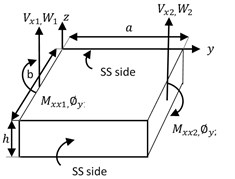
Fig. 2Boundary conditions for displacements and forces for a plate element

The displacement components of thin rectangular functionally graded plate $u_o\left(x,y,z\right)\text{,}$$v_o(x,y,z)$ and $w_o(x,y,z)$ by using classical plate theory are given by Eq. (2):

where $u^{\text{'}}(x,y)$, $v^{\text{'}}(x,y)$ and $w^{\text{'}}(x,y)$ are the mid-plate (i.e, $z=0$) displacement components.

Fig. 1. shows that the material properties are nonhomogeneous in the transverse direction, due to this the middle surface of the geometry has in-plane displacement, which cannot be neglected. Therefore, the middle surface of FGM plate geometry does not concur with the neutral surface. In this condition, the neutral surface must be changed to $z_n=z-z_0$, where $z_0$ is the distance between mid-surface to the neutral surface of the plate as shown in Fig. 1.

Hamilton’s principle is used to drive the fourth-order differential equation for transverse deflection of a thin rectangular functionally graded plate under free vibration condition and is given by Eq. (3):

The boundary conditions for Levy-type solution in Fig. 2., are given as:

where $D_{eff}=E{h}^3/12(1-{\upsilon }^2)$ is the effective bending stiffness, $h$ plate thickness, $E$ Young’s Modulus of Elasticity, $\upsilon$ Poisson’s ratio of the given material, $V_x$, $M_{xx}$, and ${\varnothing }_y$ are the shear force, bending moment and rotation of the bending plate.

3. Formulation of dynamic stiffness

A levy type solution of Eq. (3) which satisfies the boundary condition of Eq. (4) can be expressed in the following form [8]:

where $\omega$ is unknow natural frequency. By putting Eq. (5) into Eq. (3) we get Eq. (6):

The two possible solutions of the ordinary differential Eq. (6) are obtained, depending on the nature of all roots. Here we show only one possible solution:

Case 1: ${\propto }_m^2\ge \omega \sqrt{\frac{I_0}{D_{eff}}}\Rightarrow$ all roots are real (${\propto }_{1m},-{\propto }_{1m},{\propto }_{2m},-{\propto }_{2m}$):

The solution is:

The displacement $w^{\text{'}}$ in Eq. (8) and Eq. (5), shear force $V_x$, rotation ${\varnothing }_y$ and the bending moment $M_{xx}$ can be expressed in the following form using Eq. (4) as shown below:

The displacements boundary conditions for the plate are:

similarly, the forces boundary conditions are:

The displacement boundary conditions are applied, i.e., putting Eq. (12) into Eqs. (8) and (9), the following matrix relationship is obtained:

where $C_{h1}=\cosh {(\propto }_{im}b)$, $S_{h1}=\sinh {(\propto }_{im}b)$, $C_i=\cos {(\propto }_{im}b)$, $S_i=\sin {(\propto }_{im}b)$, ($i=$ 1, 2).

The force boundary conditions are applied, i.e., putting Eq. (13) into Eqs. (10) and (11), the following matrix relationship is obtained:

where $R_i=D_{eff}({{\propto }_{im}}^3-{\propto }^2{\propto }_{im}(2-\nu \left)\right)$, $L_i=D_{eff}({{\propto }_{im}}^2-{\propto }^2\nu )$ with $i=$ 1, 2. Using Eqs. (15) and (17), the dynamic stiffness matrix $K$ for functionally graded (FG) plate can be formulated by eliminating the constant vector $C$ to get Eq. (18):

where:

By using Eq. (19), the generalized dynamic stiffness matrix ($K$) as given by Eq. (20):

where six variable terms $s_{vv}$, $s_{vm}$, $s_{mm}$, $f_{vv}$, $f_{vm}$, $f_{mm}$ can be expressed in the following form [9].

4. Numerical results

The dynamic stiffness matrix is used to obtain natural frequencies of the functionally graded plate by applying the Wittrick-Williams algorithm [5]. The above procedure is used to formulate DSM and this procedure has been implemented in MATLAB program to compute the natural frequencies of the FGM plate for different boundary conditions with different power-law index ($k$) values as shown in Tables 1-3, where ${\rho }_c$ and $D_c$ are denotes the density, bending stiffness of the ceramic material. The letter m denotes the number of half-sine wave in $x$ direction, whereas $n$ represents the $n$th lowest frequency of a given value of $m$.

From Table 1, we observed that with increase in $k$ value, the natural frequencies decrease. This is because as the $k$ value increase, the metal constituent in the FGM plate and the stiffness of the plate is reduced.

When we compared the natural frequency results of the FGM plates with those available in the published literature, we found that the reported natural frequencies values at $k=0$ in Tables 2-3 are nearly same with those available in the literature [2, 11, 12]. While increasing the $k$ value from 0.5 to 1.0, the maximum error increases 5 % to 11 % as given by Chakravarty and Pradhan [12] in Table 3. The possible reasons for these reported results are discussed below.

Chakravarty and Pradhan [12] have considered mid-plane surface geometry instead of the neutral surface for solving the effective bending stiffness ($D_{eff})$, which increases the percentage error. Due to this reason, we have observed that error is smaller for $k=$0 and higher for $k=$1.

5. Conclusions

The impetus of the present work is to formulate the dynamic stiffness matrix to estimate the natural frequencies of a thin rectangular functionally graded plate, where two different sides of the plate are simply supported. Classical plate theory is used to develop the dynamic stiffness matrix of a functionally graded material plate whereas the transcendental nature of dynamic stiffness matrix is solved by using Wittrick-Williams algorithm and this formulation has been employed into MATLAB to extract natural frequency of the FGM plate with the desired accuracy. The natural frequencies calculated by DSM are compared with those available in literature.