Free vibration analysis of arch-frames using the dynamic stiffness approach

Bozyigit, Baran; Yesilce, Yusuf; Acikgoz, Sinan

doi:10.21595/vp.2020.21291

Vibroengineering Procedia

Browse Procedia

Published: 02 April 2020

Check for updates

Free vibration analysis of arch-frames using the dynamic stiffness approach

Baran Bozyigit¹

Yusuf Yesilce²

Sinan Acikgoz³

^{1, 3}Department of Engineering Science, University of Oxford, Oxford, United Kingdom

^{2, 1}Department of Civil Engineering, Dokuz Eylul University, Izmir, Turkey

Corresponding Author:

Baran Bozyigit

Cite the article Download PDF

Downloads 1414

CrossRef Citations 3

Abstract

The aim of this study is to investigate free vibration characteristics of arch-frames which consist of two columns and an arch. Firstly, an exact formulation of the problem is presented using the Dynamic Stiffness Method (DSM). The end forces and displacements of column elements are obtained analytically using Timoshenko beam theory (TBT). These are then combined with the end forces and displacements of the semi-circular arch, which is modeled with exact curved beam elements that consider axial and shear deformations and rotational inertia. By employing standard assembly and bisection based root finding procedures, exact free vibration analysis of the whole vibrating system is carried out. Then, in an effort to simplify the formulations, an approach based on approximating the arch as assembly of linear straight beam segments is presented. The calculated natural frequencies using DSM for both exact and approximate results are then tabulated for comparison purposes. The mode shapes are also compared. The results show that the proposed model simplification is effective and produces accurate mode frequency and shape estimations.

1. Introduction

The dynamic behaviour of arch-frames is of direct relevance for structural bridge engineering applications. Natural vibration frequencies and mode shapes of these structures govern their response to dynamic excitations (due to moving traffic loads, wind and earthquakes). In the literature, studies concerning vibrations of curved beams are limited when compared to literature on dynamic behaviour of straight beams. The simplest curved beam formulations [1-3] ignore shear deformations, rotational inertia and axial extensibility of the curved beam. However, these assumptions result in an overestimation of natural frequencies. A limited number of analytical studies consider the aforementioned aspects [4-7]. More specifically, these studies carry out free vibration analysis of circular beams having various boundary conditions using the DSM [4, 6, 8, 9].

This study derives exact and simplified DSM formulation of a single-span semi-circular arch-frame in Section 2. This is achieved by modeling columns as Timoshenko beams and modeling the arch as a curved beam considering axial and shear deformations and rotational inertia. To simplify this complex formulation, an approximate approach is then proposed, where the arch is modelled with equal length straight Timoshenko beam segments. The adequacy of this simplified model is then evaluated by comparing mode frequencies and shapes from this model to the exact model in Sections 2 and 3. The results are evaluated in Section 4. The main novelty of this study is based on combining the dynamic stiffness approach and segmentation of the arch into straight Timoshenko beam segments for free vibration analysis of arch-frames.

2. Model and formulations

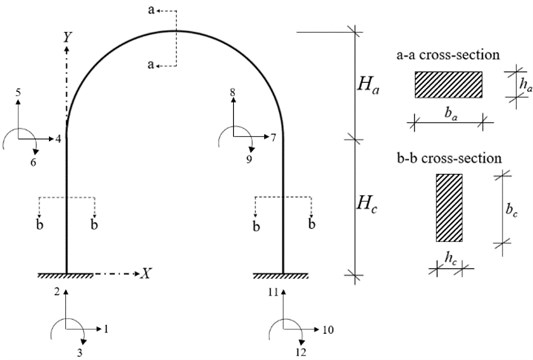
The arch-frame having 4 joints where each joint has horizontal displacement, vertical displacement and rotation presented in Fig. 1 is considered where $L_{a}$ is the span length, $X$ and $Y$ are global coordinate axes, $H_{a}$ and $H_{c}$ are height of the arch and height of the columns, respectively, $b_{a}$ and $h_{a}$ are the rectangular cross-sectional dimensions of the arch, $b_{c}$ and $h_{c}$ are the rectangular cross-sectional dimensions of the columns. The following assumptions are made: i) The behaviour of frame members is linear elastic, ii) the material of frame members is isotropic, iii) the cross-sections of frame members are uniform, and iv) the effects of damping are neglected.

Fig. 1The arch-frame model consisting of two fixed supported columns and a curved beam

In the following, only the equations of motion of the curved beam are presented. Straight Timoshenko beam formulations used here (which will be used later to describe the columns and arch segments) can be found in the literature [10]. The equation of motion of a curved beam considering axial and shear deformation and rotational inertia is written as follows [6]:

1

\begin{array}{l} \frac{A E}{R} \frac{\partial^{2} u (θ, t)}{\partial θ^{2}} - \frac{A G}{\bar{k} R} u (θ, t) + (\frac{A E}{R} + \frac{A G}{\bar{k} R}) \frac{\partial y (θ, t)}{\partial θ} - \frac{A G}{\bar{k}} ψ (θ, t) = ρ A R \frac{\partial^{2} u (θ, t)}{\partial t^{2}}, \\ \frac{A G}{\bar{k} R} \frac{\partial^{2} y (θ, t)}{\partial θ^{2}} - \frac{A E}{R} y (θ, t) - (\frac{A E}{R} + \frac{A G}{\bar{k} R}) \frac{\partial u (θ, t)}{\partial θ} - \frac{A G}{\bar{k}} \frac{\partial ψ (θ, t)}{\partial θ} = ρ A R \frac{\partial^{2} y (θ, t)}{\partial t^{2}}, \\ \frac{E I}{R^{2}} \frac{\partial^{2} ψ (θ, t)}{\partial θ^{2}} + \frac{A G}{\bar{k} R} \frac{\partial y (θ, t)}{\partial θ} - \frac{A G}{\bar{k} R} u (θ, t) - \frac{A G}{\bar{k}} ψ (θ, t) = ρ I \frac{\partial^{2} ψ (θ, t)}{\partial t^{2}}, \end{array}

where $A$ is cross-sectional area, $E$ is modulus of elasticity, $R$ is radius of curvature (equal to $L_{a} / 2$ for the semi-circular arches considered in this study), $\bar{k}$ is shear correction factor (which equals 1.2 for rectangular cross-sections), $G$ is shear modulus, $ρ$ is density, $I$ is relevant moment of inertia, $y (θ, t)$ is radial displacement function, $u (θ, t)$ is tangential displacement function, $ψ (θ, t)$ is cross-section rotation due to bending, $θ$ and $t$ are angular coordinate and time, respectively. Eq. (1) can be arranged as:

2

\begin{array}{l} a \frac{\partial^{2} u (ξ, t)}{\partial ξ^{2}} - b u (ξ, t) + c \frac{\partial y (ξ, t)}{\partial ξ} - d ψ (ξ, t) - Γ \frac{\partial^{2} u (ξ, t)}{\partial t^{2}} = 0, \\ f \frac{\partial^{2} y (ξ, t)}{\partial ξ^{2}} - g y (ξ, t) - c \frac{\partial u (ξ, t)}{\partial ξ} - h \frac{\partial ψ (ξ, t)}{\partial ξ} - Γ \frac{\partial^{2} y (ξ, t)}{\partial t^{2}} = 0, \\ p \frac{\partial^{2} ψ (ξ, t)}{\partial ξ^{2}} + r \frac{\partial y (ξ, t)}{\partial ξ} - b u (ξ, t) - d ψ (ξ, t) - z \frac{\partial^{2} ψ (ξ, t)}{\partial t^{2}} = 0, \end{array}

where $ξ = θ / Φ$ , $Φ$ is total angle of embrace of the arch (equal to $π$ for a semi-circular arch), and:

a = \frac{A E R}{{(R Φ)}^{2}}, b = \frac{A G}{\bar{k} R}, c = (\frac{A E}{R Φ}) + (\frac{A G}{\bar{k} R Φ}), d = (\frac{A G}{\bar{k}}), Γ = ρ A R, f = \frac{A G R}{\bar{k} {(R Φ)}^{2}},

g = \frac{A E}{R}, h = \frac{A G R}{\bar{k} R Φ}, p = \frac{E I}{{(R Φ)}^{2}}, r = \frac{A G}{\bar{k} R Φ}, z = ρ I .

The system has a harmonic solution. Therefore, Eq. (2) can be re-arranged by using $u (ξ, t) = u (ξ) e^{i ω t}$ , $y (ξ, t) = y (ξ) e^{i ω t}$ and $ψ (ξ, t) = ψ (ξ) e^{i ω t}$ as:

3

\begin{array}{l} a \frac{d^{2} u}{d ξ^{2}} - b u (ξ) + c \frac{d y}{d ξ} - d ψ (ξ) + β u (ξ) = 0, \\ f \frac{d^{2} y}{d ξ^{2}} - g y (ξ) - c \frac{d u}{d ξ} - h \frac{d ψ}{d ξ} + β y (ξ) = 0, \\ p \frac{d^{2} ψ}{d ξ^{2}} + r \frac{d y}{d ξ} - b u (ξ) - d ψ (ξ) + γ ψ (ξ) = 0, \end{array}

where $β = Γ ω^{2}$ , $γ = z ω^{2}$ and $ω$ is natural circular frequency. After achieving the solution of coupled Eq. (3) by usual manner, $y (ξ)$ , $u (ξ)$ and $ψ (ξ)$ can be obtained. The axial force $N (ξ)$ , shear force $Q (ξ)$ and bending moment $M (ξ)$ with $y (ξ)$ , $u (ξ)$ and $ψ (ξ)$ functions are presented in Table 1, where $\bar{c_{j}}$ are unknown constants, $s_{j}$ are characteristic roots obtained from solution of sixth order coupled Eq. (3) and:

λ_{j} = \frac{(β - f s_{j}^{2} - g) - \frac{h r s_{j}^{2}}{γ - p s_{j}^{2} - d}}{c i s + \frac{h i b s_{j}}{γ - p s_{j}^{2} - d}},

μ_{j} = \frac{b ((β - f s_{j}^{2} - g) - \frac{h r s_{j}^{2}}{γ - p s_{j}^{2} - d})}{(c i s + \frac{h i b s_{j}}{γ - p s_{j}^{2} - d}) (γ - p s_{j}^{2} - d)} - \frac{r i s_{j}}{γ - p s_{j}^{2} - d} .

Table 1Symbolic definitions of displacement and force functions

$y (ξ) = \sum_{j = 1}^{6} e^{i s_{j} ξ} {\bar{c}}_{j}$	$u (ξ) = \sum_{j = 1}^{6} λ_{j} e^{i s_{j} ξ} {\bar{c}}_{j}$	$ψ (ξ) = \sum_{j = 1}^{6} μ_{j} e^{i s_{j} ξ} {\bar{c}}_{j}$
$N (ξ)$ $= \sum_{j = 1}^{6} (\frac{A E}{R} (i s_{j} λ_{j} + 1)) e^{i s_{j} ξ} {\bar{c}}_{j}$	$Q (ξ)$ $= \sum_{j = 1}^{6} (r i s_{j} - d μ_{j} - b λ_{j}) e^{i s_{j} ξ} {\bar{c}}_{j}$	$M (ξ)$ $= \sum_{j = 1}^{6} (\frac{E I}{R Φ}) i s_{j} μ_{j} e^{i s_{j} ξ} {\bar{c}}_{j}$

3. Application of DSM

The dynamic stiffness matrix of the arch is constructed by using analytically obtained end forces and displacements. The local end displacement vector of the arch and the coefficient vector can be written as Eqs. (4-5), respectively:

4

δ = {[\begin{array}{l} u_{0} & y_{0} & ψ_{0} & u_{1} & y_{1} & ψ_{1} \end{array}]}^{T},

5

\bar{c} = {[\begin{array}{l} {\bar{c}}_{1} & {\bar{c}}_{2} & {\bar{c}}_{3} & {\bar{c}}_{4} & {\bar{c}}_{5} & {\bar{c}}_{6} \end{array}]}^{T},

where $u_{0} = u (ξ = 0),$ $y_{0} = y (ξ = 0),$ $ψ_{0} = ψ (ξ = 0),$ $u_{1} = u (ξ = 1),$ $y_{1} = y (ξ = 1),$ $ψ_{1} = ψ (ξ = 1)$ .

The end force vector of the arch ( $F$ ) is given in Eq. (6) as:

6

F = {[\begin{array}{l} N_{0} & Q_{0} & M_{0} & N_{1} & Q_{1} & M_{1} \end{array}]}^{T},

where $N_{0} = N (ξ = 0),$ $Q_{0} = Q (ξ = 0),$ $M_{0} = M (ξ = 0),$ $N_{1} = N (ξ = 1),$ $Q_{1} = Q (ξ = 1),$ $M_{1} = M (ξ = 1)$ .

The sign convention in Eq. (7) is valid for end force relations:

7

N_{0} = - N_{1}, Q_{0} = - Q_{1}, M_{0} = M_{1} .

The relations of $δ = Δ \bar{c}$ and $F = κ \bar{c}$ are obtained by using Eqs. (4-7) and Table 1 where $Δ$ and $κ$ represent coefficient matrices constructed using Eqs. (4) and (6), respectively.

The dynamic stiffness matrix of curved beam is obtained using the relation between $δ$ and $F$ as: $F = κ {(Δ)}^{- 1} δ$ , $K^{*} = κ {(Δ)}^{- 1}$ , where $K^{*}$ represents local dynamic stiffness matrix the curved beam. The global dynamic stiffness matrix of the curved beam is obtained by using the angular transformation matrix. The angular transformation matrix and global dynamic stiffness matrix of the arch are given in Eqs. (8-9), respectively:

8

A T M = [\begin{matrix} c o s (α) & s i n (α) & 0 & 0 & 0 & 0 \\ - s i n (α) & c o s (α) & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & c o s (α) & - s i n (α) & 0 \\ 0 & 0 & 0 & s i n (α) & c o s (α) & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \end{matrix}],

9

{\bar{K}}^{*} = {(A T M)}^{- 1} K^{*} (A T M),

where $α$ represents the angle between local axes at the ends of arch and global axes of the frame structure.

The same procedure is repeated for straight Timoshenko element frame members. The global dynamic stiffness matrix of the arch-frame structure is constructed by assembling these matrices. The natural frequencies are then obtained by equating the determinant of the global dynamic stiffness matrix of the arch-frame structure to zero. A root finding algorithm (based on an iterative bisection approach) is used for obtaining natural frequencies. The mode shapes can then be calculated and plotted.

4. Numerical analysis and discussions

The following geometric and material properties are considered: $L_{a} =$ 8 m, $H_{a} =$ 4 m, $H_{c} =$ 4 m, embrace angle of the arch = 180°, radius of curvature of the arch = 4 m, unit weight of frame members: 2500 kg/m³, modulus of elasticity of frame members: 3×10⁷ kN/m², Poisson’s ratio of frame members = 0.3, $b_{c} =$ 1.00 m, $h_{c} =$ 0.50 m, $b_{a} =$ 1.00 m.

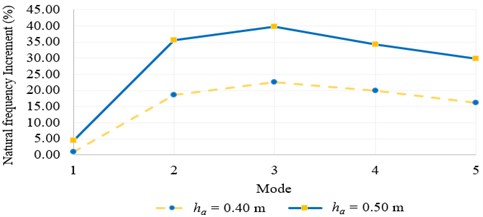
In the first part of numerical case study, the free vibration analysis of the arch-frame model is performed using exact curved beam formulations. The first five exact natural frequencies of the arch-frame are presented in Table 2 for various arch cross-sections. According to Table 2, an augmentation of arch thickness increases all natural frequencies. Fig. 2 which is plotted using the data in Table 2, represents the natural frequency increment by taking $h_{a} =$ 0.40 m and $h_{a} =$ 0.50 m, respectively. It can be observed that the first vibration mode frequency, which is dominated by column sway, is not affected significantly by changes in arch cross-section. However, as shown in Fig. 2, thicker arches have increased natural frequencies (up to 40 %) for 2nd to 5th modes.

The same arch is also described with a simpler model, where it is divided into equal length straight Timoshenko beams. Three different segmentations are considered. The lengths of straight beam segments are 2.4721 m, 1.2515 m and 0.8362 m for $n =$ 5, $n =$ 10, and $n =$ 15, respectively. It should be noted that the local degrees of freedom of the straight segments need to be rotated to global degrees of freedom during assembly (see Eq. (8)). The values of transformation angles are different for $n =$ 5, $n =$ 10, and $n =$ 15 but these values are not presented to improve the clarity of paper. The first five natural frequencies of the arch-frame using the segmented curved beam approach can be observed from Table 3 for $h_{a} =$ 0.30 m, $h_{a} =$ 0.40 m and $h_{a} =$ 0.50 m. Table 3 shows that proposed approach converges fast. The relative errors between exactly calculated natural frequencies and the results those obtained from 15 segmented arch model are presented in Table 4.

Table 2First five exact natural frequencies of arch-frame model

Mode	1st	2nd	3rd	4th	5th
$h_{a} =$ 0.30 (m)	35.3824	79.5071	146.1644	229.4268	327.6091
$h_{a} =$ 0.40 (m)	35.7264	94.3525	179.1044	274.9525	380.7456
$h_{a} =$ 0.50 (m)	36.9646	107.7696	204.2849	308.1668	425.1134

Fig. 2Increment of natural frequencies taking ha= 0.40 m and ha= 0.50 m

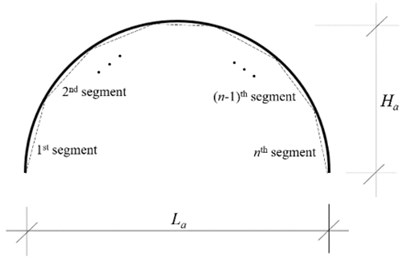
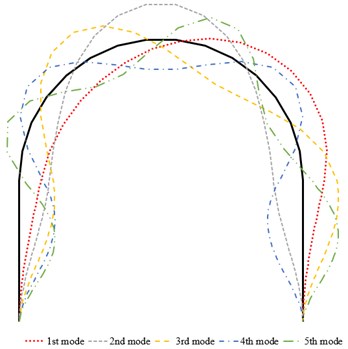
According to Table 4, the maximum relative error of proposed approach taking $n =$ 15 is 0.65 %. The segmented arch model can also be effectively used to plot mode shapes. The schematic representation of segmented arch where $n$ is total segment number and the first five mode shapes of the arch-frame model using $n =$ 15 are presented in Fig. 3. These are near-identical to exact results (not shown for clarity).

Table 3First five natural frequencies obtained by segmentation approach (rads-1)

$h_{a}$ (m)	Mode	1st	2nd	3rd	4th	5th
0.3	$n =$ 5	36.6765	83.2312	151.4298	235.7451	335.5829
	$n =$ 10	35.7016	80.4054	147.4979	231.3296	330.9019
	$n =$ 15	35.5258	79.9083	146.7663	230.2983	329.1135
	Exact	35.3824	79.5071	146.1644	229.4268	327.6091
0.4	$n =$ 5	37.1930	98.5466	184.4356	282.5921	395.9358
	$n =$ 10	36.0844	95.3759	180.4978	277.2384	385.2963
	$n =$ 15	35.8866	94.8105	179.7369	275.9985	382.8086
	Exact	35.7264	94.3525	179.1044	274.9525	380.7456
0.5	$n =$ 5	38.5939	111.8972	209.1147	318.0469	447.5858
	$n =$ 10	37.3619	108.7902	205.5938	311.0617	431.1867
	$n =$ 15	37.1421	108.2281	204.8830	309.4885	427.8523
	Exact	36.9646	107.7696	204.2849	308.1668	425.1134

Table 4Relative errors between 15 segmented arch model and exact results (%)

$h_{a}$ (m)	1st mode	2nd mode	3rd mode	4th mode	5th mode
0.30	0.41	0.50	0.41	0.38	0.46
0.40	0.55	0.60	0.42	0.45	0.65
0.50	0.48	0.43	0.29	0.43	0.64

Fig. 3a) Schematic representation of segmented arch where n is total segment number, b) first five mode shapes of arch-frame plotted using 15 segmented arch model (ha= 0.50 m)

a) Schematic representation of segmented arch where n is total segment number, b) first five mode shapes of arch-frame plotted using 15 segmented arch model (ha= 0.50 m)

a)

b)

5. Conclusions

Exact natural frequencies of an arch-frame structure having straight columns and a curved beam (considering axial and shear deformations and rotary inertia effects) are obtained. Standard DSM approaches are used for this purpose. In order to simplify the formulations, an approximate model based on segmenting the arch into straight Timoshenko beams is then considered. The free vibration analysis of both approximate and exact systems demonstrated that segmenting the arch with linear elastic elements is effective; with only a few straight segments, natural frequency and vibration mode shapes of the curved arch are accurately estimated.

Although the formulations of exact curved beams are complicated, the exact free vibration results can only be obtained using these formulations. Another advantage of using the exact end forces and displacements of the curved beam is the small size of global dynamic stiffness matrix of whole vibrating system. In contrast, while straight beam formulations are simple, segmenting the arch into straight beams increases the size of the global dynamic stiffness matrix of the system. This increases the computation time for the root finding algorithm. While this increase in computation time may be prohibitive for very large and complex systems, this is unlikely to be a problem for determining single and multi-span arch frames encountered in engineering applications.

References

Henrych J. The dynamics of arches and Frame. Elsevier, New York, 1981.

Search CrossRef
Irie T., Yamada G., Tanaka K. Natural frequencies of out-of-plane vibration of arcs. Journal of Applied Mechanics, Vol. 49, 1982, p. 910-913.

Publisher
Chidamparam P., Leissa A. W. Vibrations of planar curved beams, rings and arches. Applied Mechanics Reviews, Vol. 46, Issue 9, 1993, p. 467-483.

Publisher
Issa M. S., Wang T. M., Hsiao B. T. Extensional vibrations of continuous circular curved beams with rotary inertia and shear deformation, I: free vibration. Journal of Sound and Vibration, Vol. 114, Issue 2, 1987, p. 297-308.

Publisher
Friedman Z., Kosmatka J. B. An accurate two-node finite element for shear deformable curved beams. International Journal for Numerical Methods in Engineering, Vol. 41, 1998, p. 473-498.

Publisher
Eisenberger M., Efraim E. In-plane vibrations of shear deformable curved beams. International Journal for Numerical Methods in Engineering, Vol. 52, 2001, p. 1221-1234.

Publisher
Lee J. In-plane free vibration analysis of curved Timoshenko beams by the pseudospectral method. KSME International Journal, Vol. 17, Issue 8, 2003, p. 1156-1163.

Publisher
Caliò I., Greco A., D’urso D. Free vibrations of spatial Timoshenko arches. Journal of Sound and Vibration, Vol. 333, 2014, p. 4543-4561.

Publisher
Yang F., Sedaghati R., Esmailzadeh E. Free in-plane vibration of curved beam structures: A tutorial and the state of the art. Journal of Vibration and Control, Vol. 24, Issue 12, 2018, p. 2400-2417.

Publisher
Banerjee J. R., Ananthapuvirajah A. An exact dynamic stiffness matrix for a beam incorporating Rayleigh-Love and Timoshenko theories. International Journal of Mechanical Sciences, Vol. 150, 2019, p. 337-347.

Publisher

Cited by

Free vibrations of spatial frame structures: Analytical modelling and solution

Ömer Ekim Genel | Mertol Tüfekci | Ekrem Tüfekci

(2023)

Earthquake response of linear-elastic arch-frames using exact curved beam formulations

Baran Bozyigit

(2022)

Smoothed Particle Hydrodynamics Simulation of the Dynamic Water Pressure inside an Arch Rib of an Arch Bridge Subjected to Seismic Excitation

Ziwan Wang | Rui Li | Xiaozhang Li

(2022)

About this article

Received

11 January 2020

Accepted

19 January 2020

Published

02 April 2020

SUBJECTS

Modal analysis and applications

DOI

https://doi.org/10.21595/vp.2020.21291

Keywords

arch

dynamic stiffness method

frame

free vibration

Timoshenko beam theory

Acknowledgements

The authors would like to acknowledge the support of the Scientific and Technological Research Council of Turkey (TUBITAK) 2214-A International Doctoral Research Fellowship Programme.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2020 09 21

Vibration characteristics of Timoshenko stepped beam under moving load considering inertial effect

Shoule Wang, Dan Sun, Hongliang Li

Research article

2019 11 28

Dynamic stiffness method for free vibration analysis of thin functionally graded rectangular plates

Manish Chauhan, Vinayak Ranjan, Prabhakar Sathujoda

Research article

2018 09 30

Analytical solution for modal analysis of Euler-Bernoulli and Timoshenko beam with an arbitrary varying cross-section

Fatemeh Sohani, H. R. Eipakchi

Research article

2016 11 15

Free vibration analysis of tapered columns under self-weight using pseudospectral method

Gopinathan Sudheer, Pillutla Sri Harikrishna, Yerikalapudy Vasudeva Rao

B. Bozyigit, Y. Yesilce, and S. Acikgoz, “Free vibration analysis of arch-frames using the dynamic stiffness approach,” Vibroengineering PROCEDIA, Vol. 30, pp. 72–78, Apr. 2020, https://doi.org/10.21595/vp.2020.21291

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/vp.2020.21291
UR  - https://doi.org/10.21595/vp.2020.21291
TI  - Free vibration analysis of arch-frames using the dynamic stiffness approach
T2  - Vibroengineering PROCEDIA
AU  - Bozyigit, Baran
AU  - Yesilce, Yusuf
AU  - Acikgoz, Sinan
PY  - 2020
DA  - 2020/04/02
PB  - JVE International Ltd.
SP  - 72-78
VL  - 30
SN  - 2345-0533
SN  - 2538-8479
ER  - 

Copy Ris

Copied to clipboard!

@article{Bozyigit_2020,
	doi = {10.21595/vp.2020.21291},
	url = {https://doi.org/10.21595/vp.2020.21291},
	year = 2020,
	month = {apr},
	publisher = {{JVE} International Ltd.},
	volume = {30},
	pages = {72--78},
	author = {Baran Bozyigit and Yusuf Yesilce and Sinan Acikgoz},
	title = {Free vibration analysis of arch-frames using the dynamic stiffness approach},
	journal = {Vibroengineering {PROCEDIA}}
}

Copy Bibtex

Copied to clipboard!

[1]B. Bozyigit, Y. Yesilce, and S. Acikgoz, “Free vibration analysis of arch-frames using the dynamic stiffness approach,” Vibroengineering PROCEDIA, vol. 30, pp. 72–78, Apr. 2020, doi: 10.21595/vp.2020.21291.

Copy IEEE

Copied to clipboard!

Bozyigit, Baran, Yusuf Yesilce, and Sinan Acikgoz. “Free Vibration Analysis of Arch-Frames Using the Dynamic Stiffness Approach.” Vibroengineering PROCEDIA 30 (April 2, 2020): 72–78. https://doi.org/10.21595/vp.2020.21291.

Copy Chicago

Copied to clipboard!

Free vibration analysis of arch-frames using the dynamic stiffness approach

Abstract

1. Introduction

2. Model and formulations

3. Application of DSM

4. Numerical analysis and discussions

5. Conclusions

References

Cited by

About this article

Related Articles