Abstract
The circular cutout is considered as a typical source of stress concentrations in rectangular plate type structures. The proper position of a cutout in a rectangular plate can be significantly affected by the choice of material, cutout size, and various end conditions which are relative to the externally applied force. The research work entitled in this paper deals with the finite element formulation applied to a plate made with isotropic and laminated plates subjected to uniform pressure with various end conditions. The vicinity of stress distribution for the rectangular plate made of these two materials with and without the effect of circular cutouts is discussed. The accuracy of the solution verified with the available literature, and from the comparison, a fairly good agreement seen between the Finite element formulations in this paper with previously available results.
1. Introduction
The solution to the problem of a long rectangular plate having central hole subjected to tension was determined by Holland [1]. The stress distribution due to weakening of circular openings for rectangular plates was done by Guryer [2]. In his analysis no explicit reference is made for the length of the plate for which the results are valid. The obtained results are valid for sufficiently long / plates. A theory for evaluating stress concentration factor for thick plates made of laminated FRP was carried out by Paul and Rao [3, 4]. They used Lo-Christensen-wu higher order bending theory subjected to transverse loading. A new theory for stress analysis using rhombic array of alternating method for multiple circular holes was carried out by Ting [5]. A general form of mapping functional on arbitrary biaxial loading for stress around holes in symmetric laminates was carried out by Ukadgaonker and Rao [6]. The stress concentration of plates having various geometrical shapes embedded with the irregularities was studied by Peterson [7]. Different types of loading conditions are applied to the plates. An investigation on Elasto-plastic analysis of plate with the varying boundary conditions was studied by Sayman and Askoy [8]. From their analysis they considered the fixed-free and hinge supported boundary conditions over the metal based matrix layered composite plates with a central positioned opening. The result findings are, the determination of stress components which are based on classical lamination plate theory. A short type rectangular plates with central cutout subjected to uniform tension was studied by Troyani [9] for finding out the theoretical stress concentration factor. The analysis took the consideration of length of the member in particular the in-plane theoretical stress concentration factors for these type structures. The results are verified and validated. Two perceptions are defined while carrying out the analysis namely, one short member and other being the transition length. From the result findings, it makes clear that the other factors can have significant effect and achieve larger values than that of existing ones particularly for long type plates. The value of transition length between the long and short plates are compared and computed. Yeh and Jang [10] solved the dynamical problem of the rectangular plate using a hybrid method which combines the finite difference method and the differential transformation method. Malik and Allali [11] derived the characteristic equations of rectangular plates by utilizing DTM. Vibration analysis of simply supported rectangular plates with uni directional, arbitrarily varying thickness is proposed by Sang Wook and Sang-Hyun [12]. The plate is divided into a number of regions with constant thickness and the close-form frequency function that yields the eigenvalues of the plate is extracted by considering the condition of continuity in displacement and shape between the regions and by considering the simply supported boundary condition of plate. Narita and Leissa [13] applied Ritz method to study frequencies and mode shapes of cantilevered laminated composite rectangular plates. For axisymmetric motion, exact closed form solutions are obtained. Timothy and Nayfeh [14] developed the analysis and numerical calculations for the exact free vibration characteristics of simply supported, rectangular, thick, multi layered composite plates. It is assumed that each layer of the composite plate is of arbitrary thickness, is perfectly bonded to adjacent layers. These layers having orthotropic material symmetry and its crystallographic axes are oriented either parallel or perpendicular to the plate's boundaries. Exact formal solutions are obtained for the individual layers which are, in turn, used to relate the field variables at the upper and lower layer surfaces. The solution is carried by successive application of appropriate interfacial continuity conditions between adjacent lamina. A finite element model is developed by Liu et al. [15] for the shape control and active vibration suppression of laminated composite plates with integrated piezoelectric sensors and actuators. The model is based on the classical laminated plate theory and the principle of virtual displacements. Four-node rectangular Non-conforming plate bending elements are used to model the laminated composite plate.
2. Problem definition
For present work, the numerical computations are carried out for plates with rectangular shape having central cutout are analyzed for static stress analysis. The prediction has been carried out for evaluating the stress-behaviourial characteristics which becomes mandatory as they possess wide range of applications, for the designing of aircrafts, marine propellers blades and other locomotives. The computations are considered with and without the presence of cutout with two different materials one is Mild steel and the other being Glass epoxy material. Uniform pressure loading conditions are applied over the plate. The obtained results of stresses and deflections for various symmetric and anti-symmetric lay-ups are compared with literature. The adapted methodology from the literature and its extension to the current work may find applications in mechanical engineering and relevant research fields with the aim of reducing the stress considerable for desired features.
3. Present work methodology
Based on the applied boundary conditions of clamped free and simply supported, the stress results of rectangular plate with the effect of cutout and no cutout are considered by using the finite element based software Ansys 18.0.Various parameters of deflection, von-Misses stress, Principal stress, componential stress XYZ describing the stress behaviour of the plate are taken for consideration and comparison is based on the applied end conditions. Additionally, the effect of material change on the rectangular plate stated in terms of stress concentration is predicted and its behaviour is plotted correspondingly. Finally, based on the above parameters a comparison has been made between the isotropic and composite material. The following tables give the details about the dimensions and materials of the plate.
4. Modeling parameters of rectangular plate
Dimensions of the plate are shown in Fig. 1.
Fig. 1Rectangular Plate with central hole
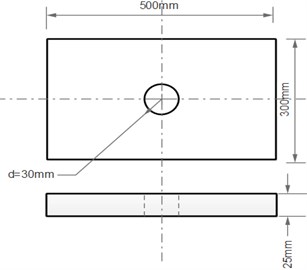
Fig. 2Rectangular plate with constraints applied
5. Material properties of the plate
Table 1MS rectangular plate properties
Properties | Values |
Elastic modulus () | 200 GPa |
Poisson’s ratio () | 0.32 |
Density () | 7850 |
Table 2Composite rectangular plate properties
Properties | E-glass-epoxy |
Density | 2100 Kg/m3 |
Longitudinal modulus | 39 (GPa) |
Transverse modulus | 8.6 (GPa) |
In-plane shear modulus | 3.8 (GPa) |
Major Poisson’s ratio | 0.28 |
Major Poisson’s ratio | 0.06 |
5.1. Validation of the result
To evaluate the accuracy of the obtained result, the existing cases in the literature are modelled and compared with the corresponding result [16]. Tables 4, 5 presents a stress and deflection comparison for a clamped boundary condition applied for the rectangular plate between the present result and results presented by [16]. The finite element model is created for which the mesh sensitivity is investigated, and the acceptable mesh is taken into consideration. The stresses obtained from a closed form of the solution are compared to those of fem models. A good agreement is examined which, provides confidence in the accuracy of the present results.
Table 3Comparison of deflection and stresses for symmetric and anti-symmetric ply-ups without cutout
Parameter | Symmetric-ply up [60/-60/-60/60]s | Anti-symmetric- Ply up [60/-60/60/60]s | ||
Present | Reference [16] | Present | Reference [16] | |
Deformation (mm) | 0.710 | 0.717 | 0.753 | 0.761 |
Max. normal stress (MPa) | 2.811 | 4.35 | 2.838 | 4.39 |
Max. normal stress (MPa) | 8.581 | 9.75 | 8.267 | 9.42 |
Max.in-plane shear stress (MPa) | 3.124 | 3.50 | 2.532 | 1.53 |
Table 4Comparison of deflection and stresses for symmetric and anti-symmetric ply-ups with cutout
Parameter | Symmetric-ply up [60/-60/-60/60]s | Anti-symmetric- ply up [60/-60/60/60]s | ||
Present | Reference [16] | Present | Reference [16] | |
Deformation (mm) | 1.246 | 1.21 | 1.255 | 1.29 |
Max. normal stress (MPa) | 7.534 | 6.5 | 10.311 | 7.17 |
Max. normal stress (MPa) | 18.340 | 14.04 | 14.233 | 13.24 |
Max.in-plane shear stress (MPa) | 5.452 | 3.95 | 6.051 | 5.44 |
Table 5Isotropic rectangular plate without cutout for clamped and simply supported boundary conditions
Parameter | Clamped-clamped | Simply supported |
Deformation (m) | 0.070852 | 0.242032 |
-component stress (MPa) | 36.5094 | 43.5011 |
-component stress (MPa) | 59.3242 | 77.3203 |
Von Mises Stress (MPa) | 52.5156 | 67.1361 |
First Principal stress (MPa) | 59.3242 | 77.3203 |
Second Principal Stress (MPa) | 18.7824 | 43.5011 |
Table 6Isotropic rectangular plate with cutout for clamped and simply supported boundary conditions
Parameter | Clamped-clamped | Simply supported |
Deformation (m) | 0.076235 | 0.273253 |
-component stress (MPa) | 38.3395 | 69.6979 |
-component stress (MPa) | 58.9374 | 131.077 |
Von Mises Stress (MPa) | 52.096 | 127.326 |
First Principal stress (MPa) | 58.9375 | 131.077 |
Second Principal Stress (MPa) | 19.0394 | 43.7032 |
Table 7Composite rectangular plate without cutout for clamped and simply supported boundary conditions
Parameter | Clamped-clamped | Simply supported |
Deformation (m) | 0.891737 | 2.53151 |
-component stress (MPa) | 32.9782 | 43.8249 |
-component stress (MPa) | 42.0697 | 60.5998 |
First Principal stress (MPa) | 62.187 | 94.3329 |
Second Principal stress (MPa) | 14.0657 | 21.8027 |
Table 8Composite rectangular plate with cutout for clamped and simply supported boundary conditions
Parameter | Clamped-clamped | Simply supported |
Deformation (m) | 0.9959 | 3.000 |
-component stress (MPa) | 34.7367 | 67.5849 |
-component stress (MPa) | 81.1568 | 113.249 |
First Principal stress (MPa) | 90.0336 | 113.249 |
Second Principal Stress (MPa) | 29.6061 | 40.1626 |
6. Results and discussions
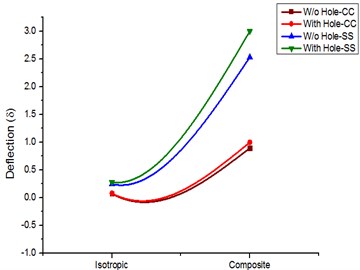
To evaluate the results, two different sets of materials aligned with two different boundary conditions are taken into consideration; the stress behaviourial characteristics of the rectangular plate made of isotropic and composite material are evaluated using the finite element method as the basic method. A comparison was made between metal plates and composites. The effect of loading uncertainties and the influence of material properties have been quantified for general safety and reliability. In addition to the uncertainties related to the above, the effects of the cutouts for both materials are taken into consideration. Based on these parameters as a reference, stepwise calculations are made for these two materials. Stress analysis was performed using Ansys numerical software, deflections and different stresses are calculated and the corresponding graphs are shown in Figs. 3-5.
– By using the clamped boundary conditions for a composite plate with symmetric and anti-symmetric lay ups subjected to static analysis, a comparison has been carried out with and without the presence of hole shown in Table 3. From the comparison, it is observed that rectangular plate with cutout having anti-symmetric ply sequence [60/-60/-60/60] with the hole has highest deflection and shear and normal component stresses.
– A comparison made between an isotropic rectangular plate with and without a hole. With the inclusion of hole for isotropic materials subjected to clamped free and simply supported boundary conditions, it is noted that rectangular plate with a cutout and simply supported boundary condition resulted in higher deformation and stress components.
– The conventional material based rectangular plate replaced with composite one and with the presence of cutout subjected to clamped free and simply supported boundary conditions it may be noted that composite rectangular plate with a cutout and simply supported boundary condition resulted in higher deformation and stress components.
Fig. 3Stress comparison for Isotropic
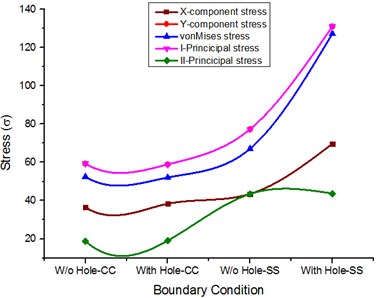
Fig. 4Stress comparison for composite materials
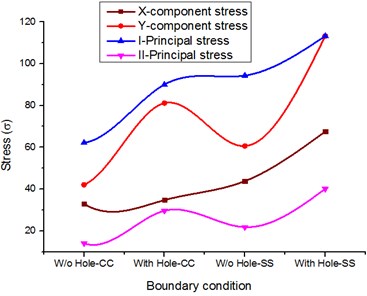
Fig. 5Deflection comparison for isotropic and composite materials
7. Conclusions
The rectangular plate with a central cutout is of practical importance in designing of the engineering structures. The effects of stress with and without hole located centrally were investigated. By validating with the previously available results, numerical investigations are carried out to investigate the effects of various end conditions acting on the rectangular plate with a central cutout. Furthermore, the solution attained is capable of considering a large variety of holes with various loading conditions. This study applies to the results for circular, elliptical and square holes. Finally, from the results obtained, it can be predicted that the value of stresses, deflections can be further enhanced by experimenting with various cutouts, bluntness, loading angle, various materials, particularly with composites they can be varied by using proper ply sequence, number of layers and ply angles.
References
-
Howland R. C.J. On the stresses in the neighborhood of a circular hole in a strip under tension. Philosophical Transactions of the Royal Society A, Vol. 229, 1930, p. 49.
-
Gur’yev N. F. The Distribution of Tension Stress in an Isotropic Finite Rectangular Plate Weakened by a Circular Opening. Scientific Annals of the Poltava Pedagogical Institute, No. 8, 1965, p. 186.
-
Paul T. K., Rao K. M. Stress analysis in circular holes in FRP laminates under transverse load. Computers and Structures, Vol. 33, Issue 4, 1989, p. 929-935.
-
Paul T. K., Rao K. M. Finite element evaluation of stress concentration factor of thick laminated plates under transverse loading. Computers and Structures, Vol. 48, Issue 2, 1993, p. 311-317.
-
Ting K., Chen K. T., Yang W. S. Stress analysis of the multiple circular holes with the rhombic array using alternating method. International Journal of Pressure Vessels and Piping, Vol. 76, 1999, p. 503514.
-
Ukadgaonker V. G., Rao D. K. N. A general solution for stress resultants and moments around holes in unsymmetric laminates. Composite Structures, Vol. 49, 2000, p. 27-39.
-
Peterson R. E. Peterson’s Stress Concentration Factors. John Wiley and Sons Inc, 1961.
-
Sayman O., Aksoy S. Elastic-plastic stress analysis of simply supported and clamped aluminum metal-matrix laminated plates with a hole. Composite Structures, Vol. 53, 2001, p. 355-364.
-
Troyani Gomes N. C., Sterlacci G. Theoretical stress concentration factors for short rectangular plates with centered circular holes. Journal of Mechanical Design, Vol. 124, 2002, p. 126-128.
-
Yeh Y. L., Jang M. J. Analyzing the free vibrations of a plate using finite difference and differential transformation method. Applied Mathematics and Computation, Vol. 178, 2006, p. 463-501.
-
Malik M., Allali M. Characteristic equations of rectangular plates by differential transformation. Journal of Sound and Vibration, Vol. 233, 2000, p. 359-366.
-
Sang Wook Kang, Sang Hyun Kim Vibration analysis of simply supported rectangular plates with uni directionally, arbitrarily varying thickness. Journal of Sound and Vibration, Vol. 312, 2008, p. 551-562.
-
Narita Y., Leissa A. W. Frequencies and mode shapes of cantilevered laminated composite plates. Journal of Sound and Vibration, Vol. 154, 1992, p. 161-172.
-
Timothy W. T., Nayfeh A. H. The vibration characteristics of thick rectangular multi-layered plates. Composites Part B, Vol. 27, 1996, p. 623-631.
-
Liu G. R., Xq Peng, Larnand K. Y., Tani J. Vibration control simulation of laminated composite plates with integrated piezo electrics. Journal of Sound and Vibration, Vol. 220, 1999, p. 827-846.
-
Sumit Rathi, Yogesh Kaushik, Sabita Madhavi Singh Behaviour of rectangular laminated composite plate with central hole under transverse loading. Proceedings of the International Conference on Modern Research in Aerospace Engineering, 2018.

