Free vibrational characteristics determination of plates with various cutouts

1. Introduction

Numerous methods have been developed for performing structural analysis of plate-like structures. Theoretical methods give a solution to such structures which are of uniform in nature in case of complexity it may become difficult to obtain a solution which may contain various boundary conditions, geometry, material properties. Consequently, one may confine to approximate numerical methods for obtaining a solution to dynamic problems. Most of the researchers have done extreme work on the free vibration analysis of plates considering various geometries of plates, cut-outs, bluntness, material properties, cut-out orientation, stress concentration factors, aspect ratios etc.

2. Literature survey

The free vibration analysis of elastic plate structures using an integral approach studied by Tanaka [1] et al. In their approach, they used the boundary integral equation method for finding out the Eigen frequency. For zero determinant value of the system matrix. This new integral equation approach resulted in the determination of the fundamental solution to the static problem. For determining the free vibration analysis of an arbitrary shaped thick plate Liu [2] used a differential cubature method a numerical technique in their analysis a linear differential operator as a continuous function having a linear sum of discrete function values are chosen for the overall domain. The free vibration analysis for frame type structures was carried by Moon and Choi [3], they developed transfer dynamic stiffness coefficient method, based on the concept of transfer of dynamic stiffness coefficient which relates to force and displacement vector at each node.

For plate type structures Myung [4] developed a finite element transfer stiffness coefficient method for free vibration analysis using a set of different boundary conditions for Kirchhoff rectangular plates, Lu [5] et al. used differential quadrature method for analyzing the vibrations. A shear deformable triangular plate element was used by Karunasena and Killipornchai [6] for free vibration analysis. A mesh free Galerkin method for unstiffened and stiffened corrugated plates was used by Liew [7] et al for free vibration analysis.

3. Finite element method

The application of finite element analysis programme is executed in Ansys18.0. The three-dimensional modeling of the plate along with various cutouts shapes are done in Solid works software, the corresponding iges file exported to Ansys solver for further analysis. The fem mesh was done using solid 185 element type; the element has the capabilities of large deflection, stiffness, plasticity, creep, stress etc.

Fig. 1Rectangular plate with rectangular and elliptical cutout

a)

b)

4. Results and discussions

The case of clamped free and simply supported boundary conditions for rectangular and square plate has been studied in the present study in which the natural frequencies and mode shapes are obtained. The effects of different cutouts positioned centrally in these plates are observed. The following observations are made to meet the desired result is as follows:

1) From Table 3 it may be observed that the rectangular plate imposed with clamped free boundary conditions with and without the presence of cutouts the plate without cutouts has attained highest operating frequencies of all the modes. If the cutouts are considered rectangular cutout has the highest first bending followed with circular cutout possess first and second torsional combined bending and edgewise bending frequencies. The second bending frequency will be higher for the elliptical cutout.

2) From Table 4 with the change of plate from rectangular to square type with taking same cutout sizes into consideration No cutout followed by circular cutout attained highest operating frequencies except for second bending frequency.

3) Table 5 signifies that with the change of boundary condition from clamped free to simply supported type the natural frequency has been enhanced to 20 % of its original frequency. with the inclusion of cutout, the values of the second torsion, combined bending and edgewise bending are higher for No cutout type, whereas first bending will be higher for elliptical followed by square and rectangular types for first torsion and second bending frequencies.

4) From Table 6 the square plate with simply supported type boundary condition it makes clear that first bending will be higher for elliptical type cutout followed by No cutout type will be attaining higher frequencies from the first torsion to edgewise bending.

Fig. 2Effect of no cutout and rectangular cutout on natural frequencies of rectangular and square plate

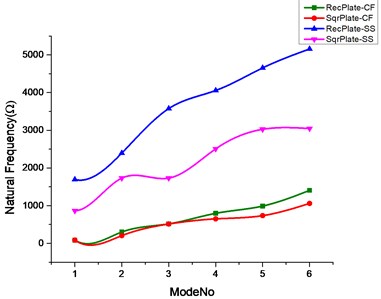
a)

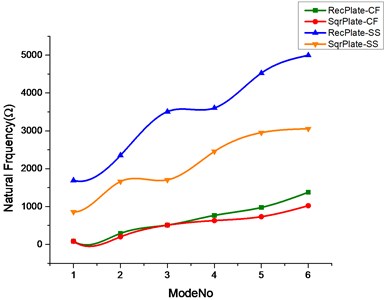
b)

Fig. 3Effect of square and elliptical cutout on natural frequencies of rectangular and square plate

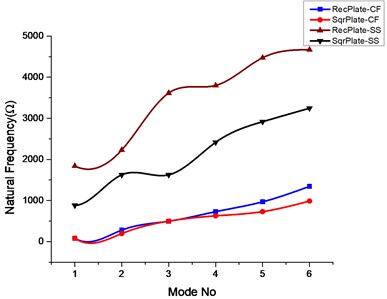
a)

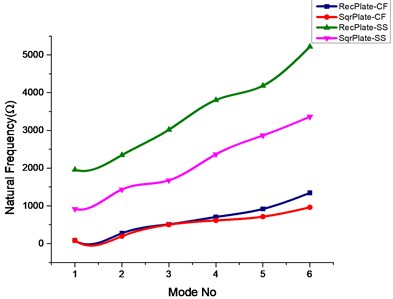
b)

Fig. 4Effect of triangular and circular cutout on natural frequencies of rectangular and square plate

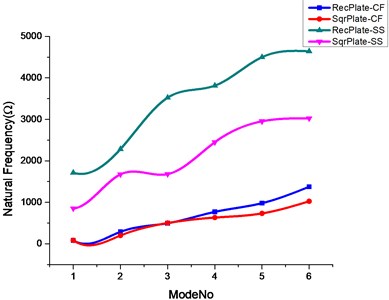
a)

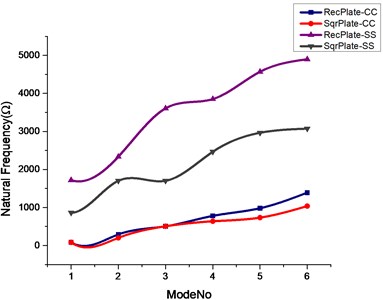
b)

5. Conclusions

In this study, the modal analysis is carried out using finite element software for rectangular and square plates to predict the modal frequencies. Various boundary conditions imposed over the plate are investigated. The effects of various Cutouts on the mode shapes are investigated. From the results, it is observed that the inclusion of Cutout has a significant effect on the modal frequency. Plates of Square and rectangular without Cutout and subjected to clamped free boundary condition has attained higher operating frequencies. When the boundary condition has changed from clamped free to simply supported type except for first bending frequency, the remaining frequencies are higher for no Cutout type. Later to no cutout case the inclusion of circular cutout in all the remaining cases irrespective of boundary conditions, types of plates obtained good operating frequencies. The operating frequencies for such case can be further enhanced by varying the material, changing the orientation of cutout, bluntness etc.