Abstract
To process the non-stationary vibration signals and improve accuracy of bearing fault diagnosis, this paper presents a novel intelligent fault diagnosis method based on the adaptive fast ensemble empirical mode decomposition (AFEEMD) and one-dimensional convolutional neural networks (1D CNNs). First, the AFEEMD algorithm is utilized to decompose the raw signals into intrinsic mode functions (IMFs). Then, the time and frequency statistic features of the first several IMFs are analyzed to form feature vector, which are used as the input of 1D CNNs to identify the bearing fault. The performance of the proposed method is validated using the dataset from the Case Western Reserve University (CWRU). Compared with the traditional back propagation neural network (BPNN), the results show that the proposed AFEEMD-1D CNNs method not only can obtain higher accuracy and achieve more reliable performance, but also can improve the generalization performance. Due to the end-to-end feature learning capacity, it can be extended to other machinery for fault diagnosis.
Highlights
- This paper presents a novel intelligent fault diagnosis method based on the adaptive fast ensemble empirical mode decomposition (AFEEMD) and one-dimensional convolutional neural networks (1D CNNs).
- The experiment results demonstrate that the proposed method can obtain higher accuracy and achieve more reliable performance.
- The experiment results also verify that the proposed method can improve the generalization performance.
1. Introduction
The bearings are the crucial component of the rotating machinery. Their operation condition directly affects the accuracy and stability of the rotating machinery. Once faults occur, it can result in serious casualties and economic losses, so numerous fault diagnosis approaches are presented. Due to the overwhelming background noise, it is difficult to accurately identify the bearing minor fault states. In addition, the collected bearing signals are non-station, the traditional vibration analysis techniques, such as fast Fourier transform (FFT), is failure to signal processing. As an adaptive analysis method, the EMD is constantly improved and can decompose the complex signals into IMFs. It is effectively used to process the non-liner, non-station signals for fault diagnosis [1, 2]. In this study, we utilize the AFEEMD method as preprocessing technique which can better eliminate the noise residuals, extract important features, and improve the EMD efficiency [3]. The statistic features in time domain and frequency domain of the first several IMFs are used to form feature vector which represents the most of fault information [4]. It will be used as the input of the 1D CNNs. The most advantage is that the input dimension and complexity of the 1D CNNs model can be reduced. It is conducive to reduce the training time.
Recently, the deep neural networks (DNNs) have been succeeded in fault diagnosis. Due to the advantage of shared filters, the convolutional neural networks (CNNs) can tackle with the problem that the parameters of a regular fully connected DNN grows exponentially when the more layers are added [5]. Sun et al. [6] proposed a CNN-based fault diagnosis method for gears and obtained a higher accuracy, where the dual-tree complex wavelet transform (DTCWT) was used to extract the signals’ features. The experiment demonstrated the effectiveness of the proposed method. However, numerous traditional CNNs methods for fault diagnosis use two-dimensional images as input, ignoring the vibration signal with one-dimensional characteristics. The vibration signal is only related to the one-dimensional (1D) time series. The 2D image as input may destroy the spatial correlation in original sequence and the related fault information may be lost. In addition, the 1D CNNs model only needs 1-D convolutions (scalar multiplications and additions), so it is more efficient and cheaper for the speed and hardware.
Inspired by the advantage of AFEEMD and 1D CNNs, we present an intelligent bearing fault diagnosis method based on the AFEEMD and 1D CNNs in this paper.
2. The basic theory of AFEEMD and 1D CNNs
2.1. AFEEMD
The empirical mode decomposition (EMD) can decompose the signal into IMFs: , ,…, and a residue signal . The IMFs include different frequency bands and imply a distinct time characteristic scale. It can be expressed as:
In the process of decomposing complex vibration signals, the ensemble EMD (EEMD) is used to eliminate the mode mixing problem. The EEMD adds the white noise in the data analysis, and it can clearly separate the natural scale of signals. The complete ensemble empirical mode decomposition (CEEMD) algorithm [7] adds positive and negative pairs of white noise to the observed signal, which can better eliminate noise residuals. Based on the CEEMD algorithm, the generated adaptive noise is added to the signal in pairs. Fast ensemble empirical mode decomposition (FEEMD) [8] optimizes stopping criteria and improve the EEMD efficiency. To better eliminate the noise residuals and improve the EEMD efficiency, the AFEEMD is finally proposed. It has been proved that this approach can work effectively [3].
2.2. 1D CNNs
The 1D CNNs model is a typical feedforward end-to-end neural networks, which essentially extracts the characteristics of input data by establishing multiple filters. A typical 1D CNNs model includes an input layer, several convolutional layers, several pooling layers, several fully-connected layers and an output layer.
(1) Convolutional layer.
In this paper, the collected vibration signals are time series, so 1D convolutional operation is used to construct the 1D CNNs, which is more suitable for feature extraction of vibration signals. The forward propagation (FP) from convolution layer to the layer can be described as follows:
where and represent the weights and biases of the -th filter kernel in layer , respectively; the notation denotes the 1D Convolutional operation; is the -th local region in layer ; is the input of the -th neuron in frame of layer .
(2) Activation operation.
After the convolutional layers, the activation function is utilized to obtain nonlinear feature relationship of the input signal. Recently, rectified linear unit (ReLU) activation function can improve the representation ability and accelerate the convergence of 1D CNNs. ReLU is given by:
where is the output value of convolution layers and is the activation value of .
(3) Overlapping max-pooling layer.
The pooling operation is a self-sampling process, which achieves spatial invariance. It can reduce parameters and improve model generalization performance. A common pooling method is to take the maximum or average value of all neurons for a local feature. The max-pooling operation can be expressed as:
where is the value of -th neuron in the -th frame of layer ; is the width of the pooling region, and represents the result of the pooling operation.
Different from the traditional pooling operation, this paper uses the overlapping max-pooling, that is, the step size of the window movement is smaller than the size of the window itself, which can improve the prediction accuracy and alleviate overfitting to a certain extent.
3. Proposed method
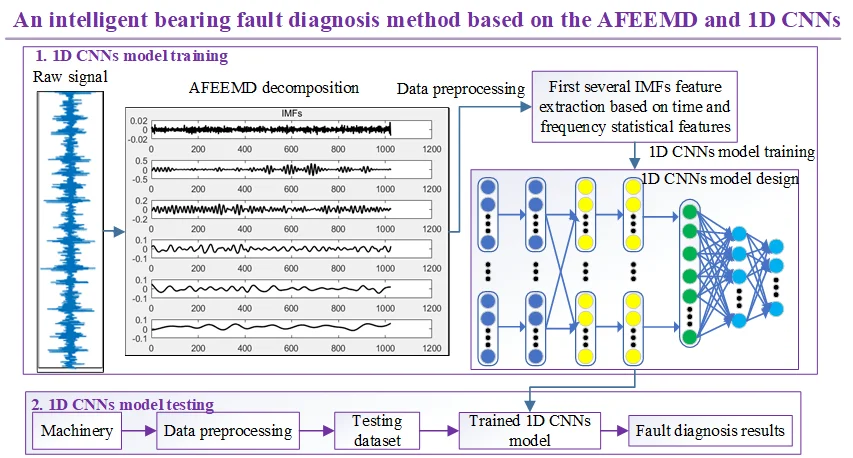
This paper presents an intelligent end-to-end data driven method for bearing fault diagnosis based on AFEEMD and 1D CNNs. Fig. 1 shows the framework for the AFEEMD-1D CNNs method. There are three main procedures, and the detail description is as follows.
Fig. 1Framework for proposed method based on the AFEEMD and 1D CNNs
(1) Data preprocessing: Each raw signal with 1024 length is decomposed by the AFEEMD. The 14 time domain and 4 frequency domain of statistic features for decomposed IMFs are calculated to obtain the high-dimensional feature input data. The AFEEMD algorithm is used to improve of signal decomposition and reduce computation time, and it can extract most of the fault information in the raw signal. The 18 statistics features of each IMF in parallel superposition form a feature input vector. The advantage of this is that the input dimension and the parameters of the 1D CNNs model are greatly reduced. Hence, the overall time of the training is reduced.
(2) 1D CNNs model establishing and training: Most of the CNNs model with 2D convolution structure is used to pattern recognition. But the vibration signal has one-dimension (1D) characteristic, and is only related to the 1D time. In addition, the 1D CNNs model only needs 1-D convolutions (scalar multiplications and additions), so it is more efficient and cheaper for the speed and hardware. In this 1D CNNs model, the dropout algorithm is used in the fully-connected layer to prevent overfitting which is a common problem in training. The overlap max-pooling skill is also utilized to improve the accuracy of the 1D CNNs. To demonstrate the generalization performance of the proposed method, the training and testing dataset are collected from the different working conditions. The training dataset formed by the data preprocessing at working condition 1 is used to train the initialized 1D CNNs model by adjusting the error between the actual and predicted label. After the training process, the parameters are saved for testing.
(3) 1D CNNs model testing: The testing dataset collected from working condition 2 is used to evaluate the generalization capability and accuracy of the trained model.
4. Experimental verification
4.1. Bearing test rig and data acquisition
In this paper, the bearing signals are investigated to demonstrate the effectiveness of the proposed method. The public bearing data collected from the CWRU are analyzed [9]. The test rig is shown in Fig. 2, which includes a 2-hp motor, a torque transducer, and a dynamometer.
Fig. 2Experimental setup used for bearing fault diagnosis

In this case study, the vibration signals collected from the driven end bearing are used. There are four types data under different working conditions, including the normal (N), inner fault (IF), ball fault (BF), and outer fault (OF). The sampling frequency is 48 kHz, and the fault samples are the 0.18 mm damage severity. To further prove the generalization performance of this method, the training dataset collected from working condition at the 1hp load and 1772 rpm motor speed, and the testing dataset is 2 hp load and 1750 rpm. The former all has the 1840 samples, the latter is 360 samples. The detail description of the dataset is shown in Table 1.
Table 1The detail description of the bearing training and testing dataset
Motor speed (rpm) | Load (hp) | Number of samples | Fault type | Label | |
Training / Testing dataset | 1772/1750 | 1/2 | 460/90 | N | 1 |
460/90 | IF | 2 | |||
460/90 | BF | 3 | |||
460/90 | OF | 4 |
Each raw sample has 1024 sampling points. Then it is decomposed by AFEEMD, and the IMFs component is obtained. The all 18 statistical features in the time domain and frequency domain of the first six IMFs are respectively calculated to form feature input sample which comprehensively expresses most of the fault information. Hence, the dimension of each preprocessing sample is 108, which is used as the input of the 1D CNNs. The hyper parameters of the 1D CNNs are listed in Table 2. The epoch number is 100, and the dropout is 0.5. To verify the effectiveness of the proposed method, the average accuracy, standard deviation, and computing time are used as the evaluation indexes.
Table 2Hyper parameters of the 1D CNNs
Layer type | Convolution 1 | Pooling 1 | Convolution 2 | Pooling 2 | Fully-connected | Softmax |
Kernel size | 3 | 3 | 3 | 3 | 100 | 4 |
Number | 16 | 16 | 32 | 32 | 1 | 1 |
Stride | 1 | 2 | 1 | 2 |
4.2. Results
In order to evaluate the stability of proposed method, six trials are carried out. For comparison, the BPNN is utilized to analyze the same dataset. The structure of the BPNN is 108-40-10-4, and the epoch number is 500. Table 3 lists the results of the testing accuracy, standard deviation, and time. It can be observed from Tables 3 that the average testing accuracy is 98.24 % by using the proposed method, which is higher than 81.62 % by using the BPNN. It proves that the proposed method can achieve high accuracy and possess good generalization performance. The standard deviation of the proposed method is 0.33 %, and it is smaller than the 1.00 % of BPNN, which shows a more stable performance. Due the feature vector as the input of 1D CNNs, it reduces the training time and complexity of the network. The computing time of the proposed method is 22.5 s, which is the same as the traditional BPNN of 21.67 s.
Table 3Diagnosis results of the two methods in six trials
1 | 2 | 3 | 4 | 5 | 6 | Average | Standard deviation | Time (s) | |
Proposed method | 98.61 | 98.06 | 98.33 | 98.61 | 98.06 | 97.78 | 98.24 | 0.33 | 22.5 |
BPNN | 82.22 | 80.83 | 81.39 | 80.28 | 83.06 | 81.94 | 81.62 | 1.00 | 21.67 |
The Fig. 3 shows the confusion matrix of the two methods. It contains the information for classification and misclassification samples. The horizontal axis represents actual condition of classification, and the ordinate axis represents predicted condition for samples. From Fig. 3, we can find that condition 3 has the lowest accuracy, namely, there are three misclassified samples with ball fault.
Fig. 3Condition classification confusion matrix of the proposed methods for the first trial
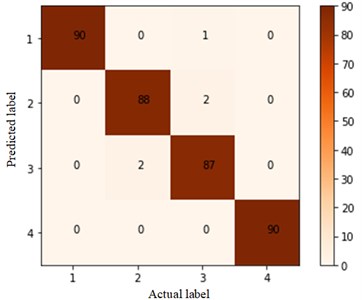
Table 4 displays fault diagnosis result of each category for the first trial using the proposed method and BPNN. Only the classification accuracy of bearing outer fault through the proposed approach is the same as the BPNN. The proposed method performs better in other conditions and obtains the highest overall testing accuracy of 98.61 %. It achieves the end-to-end feature learning based on the AFEEMD.
Table 4The fault diagnosis results of the two methods
Normal | IN | BF | OF | Overall | |
Proposed method | 100 | 97.78 | 96.67 | 100 | 98.61 |
BPNN | 83.33 | 67.68 | 77.78 | 100 | 82.22 |
5. Conclusions
In this paper, we propose an intelligent fault diagnosis for rolling bearings based on the AFEEMD and 1D CNNs. To better eliminate the noise residuals and improve the EEMD efficiency, the AFFEMD is used to decompose the raw vibration signals into IMFs. To reduce the input dimension and complexity of the 1D CNNs, the statistic information in time domain and frequency domain of the first several IMFs is utilized to form feature vector. The 1D CNNs model is exploited to identify the bearing fault diagnosis. The spatial correlation in original sequence for vibration signals related to the 1D time can't be destroyed by the 1D CNNs, and it only needs 1D convolutions (scalar multiplications and additions), so it is more efficient and cheaper for the speed and hardware. Compared with the BPNN, the proposed AFFEMD-1D CNNs fault diagnosis method not only can effectively improve the efficiency and stability, but also can achieve higher accuracy and better generalization performance under variable working condition.
References
-
Georgoulas G., Loutas T., Stylios C. D., Kostopoulos V. Bearing fault detection based on hybrid ensemble detector and empirical mode decomposition. Mechanical Systems and Signal Processing, Vol. 41, Issues 1-2, 2013, p. 510-525.
-
Wang H., Liu Z., Song Y., Lu X. Ensemble EMD-based signal denoising using modified interval thresholding. IET Signal Processing, Vol. 11, Issue 4, 2017, p. 452-461.
-
Sun H., Wang H., Guo J. A single-channel blind source separation technique based on AMGMF and AFEEMD for the rotor system. IEEE Access, Vol. 6, 2018, p. 50882-50890.
-
Nguyen V. H., Cheng J. S., Yu Y., Thai V. T. An architecture of deep learning network based on ensemble empirical mode decomposition in precise identification of bearing vibration signal. Journal of Mechanical Science and Technology, Vol. 33, 1, p. 41-50.
-
Xia M., Li T., Liu L., Silva C. W. D. Fault diagnosis for rotating machinery using multiple sensors and convolutional neural networks. IEEE/ASME Transactions on Mechatronics, Vol. 23, Issue 1, 2017, p. 101-110.
-
Sun W., Yao B., Zeng N., Chen B., He Y., Cao X., He W. An intelligent gear fault diagnosis methodology using a complex wavelet enhanced convolutional neural network. Materials, Vol. 10, Issue 7, 2017, p. 1-18.
-
Deng X., Pang L., Jiang K., Wang X. Single-channel blind signal separation method for time-frequency overlapped signal based on CEEMD-FastICA. IEEE 13th International Conference on Signal Processing (ICSP), 2016.
-
Wang Y., Yeh C., Young H., Hu K., Lo M. T. On the computational complexity of the empirical mode decomposition algorithm. Physica A: Statistical Mechanics and its Applications, Vol. 400, 2014, p. 159-167.
-
Case Western Reserve University. Bearing Data Center Website. https://csegroups.case.edu/bearingdatacenter/pages/welcome-case-western-reserve-university-bearing-data-center-website.
