Mathematical modelling of the rotary engine

1. Introduction

Many commercially available software products are used for the reciprocating-piston engine prediction simulations, this software reduces the time needed for the engine development in the early stages as well as the fine tuning of the engine during the final pre-production testing. As the demand for the reciprocating-piston engines is incomparable to that of the rotary engine, the 1D simulation software is exclusively made for the prior engine type. During the development of the rotary engine it is advisable to use the advances of said software. Unfortunately, the direct use of this software isn’t possible because of the following differences between the two engine designs:

• The ratio of the main shaft rotation to the 4-stroke cycles of the rotary engine is equal to 3. Single cylinder 4-stroke piston engine crankshaft rotates twice for the same quantity of cycles.

• The difference of the surface to displacement ratio during the main-shaft rotation.

• The difference in the heat-transfer proprieties coming from the differences in the geometric shape of the combustion chamber.

• The length of the combustion chamber increases the time of the combustion process, which reduces the overall efficiency of the combustion.

• The movement of the working chamber across the whole loop of the main housing influences the difference in the temperature distribution of the engine. The speed of this process also influences the speed of the flame propagation through the working camber as the leading apex seal of the rotor is constantly moving forward from the flame-front.

These differences are prohibiting the direct use of a reciprocating-piston engine prediction software and this paper will discuss the methods that can be applied to creating the virtual reciprocating-piston engine used for solving the mathematical model created by the 1D simulation software with comparable performance of the developed rotary engine.

2. Virtual engine creation

Main concern in the virtual reciprocating-piston engine design is the dimensional equality between the two engine designs. For the validation of the mathematical model, Aixro XR 50 engine was used and measured, see Table 1.

The surface and the volume of the combustion chamber is to be equal through the whole range of the main shaft rotation. For this criterion the kinematic simulation was prepared, giving the surface area and the volume of the working chamber of the Aixro engine for the variable main-shaft angle. As the input of the 1D simulation software needs to be in the dimensions of the piston engine (bore, stroke, piston position in relation to the main shaft angle of rotation), said parameters were chosen to provide the equality of surface area and the volume of the working chamber during the engine cycle. In the solver the head area of the piston engine remains constant, as this is not the case in the rotary engine, where the head area equals to the area of the main housing belonging to the working chamber at the given rotation of the main shaft, the weighted average of this area was taken as the least error producing method. The averaging method used was weighed by the preliminary heat transfer prediction during the engine cycle.

Fig. 1Head equivalent surface area of the virtual piston engine calculation using the weighted average

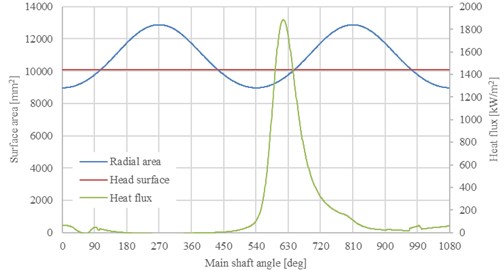
As the ratio of the rotating speed of the main-shaft of the rotary engine to the crank shaft of the reciprocating-piston engine is 3/2 as stated before and the rotary engine having three combustion chambers due to its basic design, the 4-stroke three-cylinder engine was chosen as the best substitute in the 1D simulation software. From the equality of the output power of the two engines, the rotating speed of the virtual engine must be set to 2/3 of the rotary engine. This is the main requirement of the successful simulation outcome as this constant will influence the torque calculations.

3. Heat transfer properties

The heat transfer properties are influenced by the different geometric shape of the combustion chamber, the approach used in [1] was used to determine the heat transfer coefficient in the work chamber. The [2] states that the heat transfer coefficient (HTC) calculated using the previous method is greater than the value calculated by the commercial piston 1D simulation software by 10 to 15 %. Taking this into the consideration, the overall HTC was increased by 15 %. The heat transfer from the combustion process to the surrounding work chamber walls is than calculated by the software using the surface area data from the kinematic simulation, the temperature of the work chamber walls derived from the data measured at the NKU testing facility [3] and the temperature of the working fluid inside the engine computed from the heat generation of the burned fuel using Wiebe model. The coefficients used in the Wiebe model were estimated using the available literature [4-6]. The final combustion ratio was estimated to be 0.975 which corresponds to the Wiebe coefficient $A$ = 3.71 and the form factor “M” of 3 was chosen to be the best representative of the combustion process. The Wiebe equation has the form as follows:

For the duration of the combustion process of 75 degree of the main shaft rotation which translates to 50 degree of the virtual engine crankshaft rotation.

4. Flow simulation of the engine ports

For the first iteration of the port flow coefficients calculation, the 3D CFD method was used. As the experimental method of using the blow through mass-flow measuring station cannot be executed in the early stages of the development due to the lack of the physical engine model, using the commercial computational software is the only option to determine these parameters. The discharge coefficients of the intake and the exhaust system were computed at the major points of the system. Intake and the exhaust port opening and closing discharge coefficients were approximated by the linear function as this approach reduces the time needed for the 3D CFD method and can be used without large error as presented in the [2]. Due to the complexity of the axial intake system on the simulated engine, two simulations were carried out. The results of the simulations were than used to calibrate the 1D model of the virtual piston engine.

The geometry of the engine was modelled according to the measurements done on the Aixro XR 50. The simulation in the 1D software was than run for steady state conditions at wide open throttle for the RPM range of 4500 to 9400.

5. Results

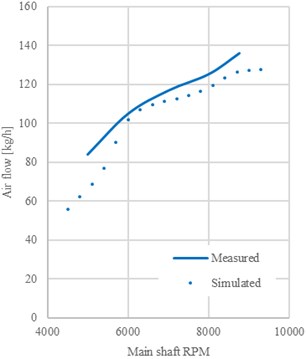
Using the previous input data calibrations from the known engine, the simulation was run to evaluate the concept of the virtual piston engine creation. For the engine performance the average difference of the simulated and the measured values was 3.08 %, see Fig. 2. Torque and power are the overall engine characteristics which determine the quality of the method used in the simulation, but for the previously mentioned discharge coefficient calibration validation of the 1D model engine air mass flow is used, see Fig. 3.

Fig. 2Engine power and torque performance chart, measured values are dotted

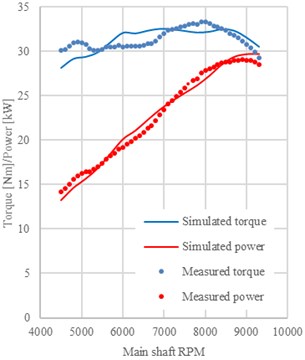
Fig. 3Mass air flow chart used for the validation of the discharge coefficients

6. Conclusion

As the commercially available software for thermodynamic simulation of the rotary engine is not available due to the comparably low market demand to the reciprocating-piston engine type, the available software input can be modified to provide accurate simulation results. The method of creating the virtual piston engine is shown using the calculated bore, stroke and piston position data to provide the equivalent surface area and volume of the working chamber. The calculation method using 3D CFD software was applied for the complicated axial intake of the engine. Using the outcome of the 3D simulation, the 1D simulation model was calibrated to provide the comparable mass air flow results. The heat transfer coefficients were calculated using the forced convection over the flat plane analogy. These results are than used as the weight for the average calculation of the head surface area which remains constant in the reciprocating-piston engine but changes with the angle of the main-shaft in the rotary engine.

For the future work the testing is required to measure the in-cylinder pressure data and the temperature and pressure data from the engine intake and the exhaust system as these are to be used for the model calibration. Using this model method, the new rotary engine unit parameters can be designed, optimized and the performance predicted.