Informative frequency band identification method using bi-frequency map clustering for fault detection in rotating machines

1. Introduction

he area of machine diagnostics is often based on the analysis of vibration signals. In such signals, damage-related information is located in an Informative Frequency Band (IFB) [1]. The width, the location and the consistency of the band depends on numerous factors, i.e. the type of damage, the operational conditions, the kinematic structure and the damage location in the machine. In many cases those factors and information about the IFB are not known. Regarding such constraints, it is understandable that research on data-driven methods is a highly pursued direction. Various methods for IFB detection have been proposed over the last years, such as the usage of spectral kurtosis [2], selectors [3], the protrugram [4], and many others. However, it is very important that not only IFB-related techniques have been successfully developed over recent years. Examples of other directions and approaches include the selective time analysis in time-frequency domain [5], the multichannel information fusion [6], the time-varying filtration [7], or the heavy-tailed distributions modeling [8-10]

In the presented work the authors attempt to determine the IFB based on a bi-frequency map clustering. In this case the modulation spectra vectors are considered as points in the multidimensional feature space and each carrier frequency bin holds a single point. An Expectation-Maximization technique is used to cluster such data, which allows to obtain a precisely bounded IFB. The boundaries of the appropriate cluster are used to design a bandpass filter allowing the extraction of the damage-related impulsive component from the signal.

2. Methodology

The proposed procedure consists of three main steps. Firstly, the bi-frequency representation of the vibration signal is calculated. In particular the Cyclic Spectral Coherence is used. Secondly the Expectation-Maximization technique is used to cluster individual modulation spectra (for each carrier frequency bin). Finally, the boundaries of the cluster of the CSC map, that can be interpreted as containing the informative frequency band, are used to construct a bandpass filter for impulsive component extraction.

All these techniques are well-known, however their combination is proposed as a successful approach in condition monitoring, focusing specifically on cases, where an impulsive damage-related component investigation is needed but on the other hand a meaningful determination of the IFB is difficult using simpler methods. In this section the definitions and the main properties of the proposed methodology are briefly introduced. Their fusion is illustrated and described afterwards.

2.2. Expectation-Maximization clustering algorithm

The Expectation-Maximization (EM) algorithm is an optimization method for the estimation of parameters for given measurement data $X$ [13, 14]. EM is especially targeted for separating mixed Gaussian distributions (or any other distribution) in the considered feature space. It is constructed using two main steps which are iterated alternately until achieving the convergence. Clustering in multiple dimensions is the most classic application of this method.

Fig. 1Raw input signal

It is very important to be aware of the limitations of the EM methodology. It only approximates the maximum likelihood estimate and does not guarantee finding the theoretical value. If the function of likelihood is not concave, EM does not guarantee to find the global maximum of the function. In practice, it should not be executed only once. Usually one should repeat the EM several times with random initialization and select the one presenting the more effective result. In this paper EM has been run 10 times.

3. Application to industrial data

In this article, a vibration signal measured on a rolling bearing is investigated. The bearing is a part of a drive pulley installed in a belt conveyor driving station. The signal is presented in Fig. 1. The sampling frequency has been selected equal to 19.2 kHz. The signal contains a single wideband impulsive component corresponding to local damage of the outer race. The interested readers may find more detailed information regarding this machine to the Ref. [15].

Fig. 2Top: Cyclic Spectral Coherence map of the input signal; Middle: Layout of obtained clusters along the modulating frequency dimension; Bottom: Bandpass filter designed based on obtained clustering results

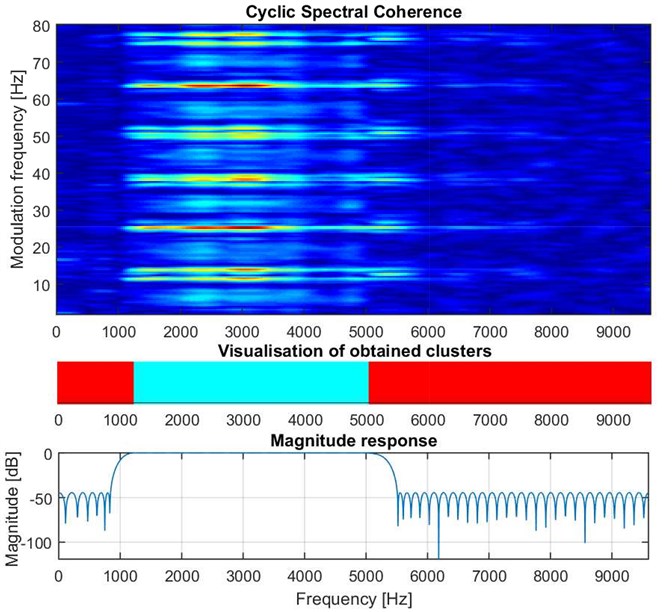
The Cyclic Spectral Coherence map of the signal is presented in the top panel of Fig. 2. In the middle panel there is a visual representation of the clustering results, with the carrier frequency axis aligned with the CSC map. EM correctly focuses on the essential part of the carrier frequency band that contains the information about the damage component. The lower and the higher cutoff frequencies of this cluster have been identified equal to 1204 Hz and 5005 Hz respectively. Based on those values, an equiripple bandpass Finite Impulse Response (FIR) filter has been designed using a filter design tool available in Matlab software (see Fig. 2 bottom panel).

Fig. 3Extracted damage-related impulsive component

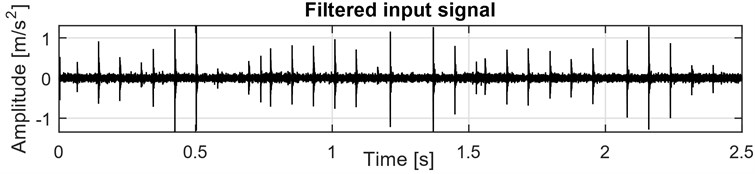
The obtained filter has been used to filter the input vibration signal. As a result, the impulsive component has been extracted allowing for a clear and precise observation of damage-related impulsiveness, which is present in the signal.

4. Conclusions

In this paper the authors presented a new method for local damage detection using bi-frequency map clustering for informative frequency band identification, applied to a real vibration signal emitted by a faulty bearing. Instead of using clustering of two-dimensional data representation for recognizing the location of individual impulses in time (in case of using time-frequency maps as a base domain) or in modulating frequency domain (for bi-frequency maps), the Expectation-Maximization algorithm is used in order to identify the Informative Frequency Band on the Cyclic Spectral Coherence map, which is then used to construct the bandpass filter for the processing of the original signal. The results demonstrate the effectiveness of the method to successfully identify the impulsive component of the signal related to the machine fault.