Free vibration of functionally graded SWNT reinforced aluminum alloy beam

1. Introduction

SWNT are an important variety of carbon nanotubes. SWNT possesses exceptional mechanical, electrical and thermal properties. The application of the concept of FGM to SWNT composites has led to design different components satisfying particular properties [1]. FG SWNT reinforced composites are a new composite material having different applications in aerospace, defense, energy, automobile, medicine, structural and chemical industry [2]. The efficiency of SWNT as reinforcement can be attributed to the load transfer mechanism from matrix to SWNT at nanoscale. Interfacial bonding in the interphase region between embedded SWNT and its surrounding polymer is a key factor for the load transfer and reinforcement phenomena [3].

Al-alloys are broadly used in diverse applications like aerospace, automotive as well as chemical industries due to its distinct properties as compared to other metals [4]. Because of the extraordinary physical and chemical properties of SWNT, reinforcement of Al-alloys with this type of material leads to huge changes in its properties like greater strength, improved stiffness, reduced density, improved high temperature properties, improved abrasion and wear resistance [5, 6].

Most of the studies in SWNT reinforced composites are concentrated on the effect of the reinforcement volume fraction on the mechanical properties [7, 8] but research on vibration analysis of FG SWNT reinforced composite structures is limited to a few published articles. In the following, some of the recent published works on the dynamic characteristics of FG SWNT reinforced composite beams.

Heshmati and Yas [9] investigated the improvement of the fundamental natural frequency of FG SWNT reinforced polymer composite beam. The governing equations are found using the Euler-Bernoulli beam theory. The effect of SWNT agglomeration, distribution and boundary conditions on the dynamic behavior of the beam is found to be very important. The work carried out recently by Shenas et al. [10] presented the free vibration behavior of the pre-twisted FG SWNT reinforced composite beams in thermal environment. The third-order shear deformation beam theory is used to obtain the governing equations. The Chebyshev-Ritz method is used to determine the free vibration eigenvalue equations. The FG beam is found to be sensitive to the pre-twist angle and to the temperature. The free vibration of nanocomposite Timoshenko FG beams reinforced with SWNT resting on an elastic foundation is studied by Yas and Samadi [11]. The SWNT are assumed to be aligned and straight with a uniform layout. The rule of mixture is used to describe the effective material properties of the nanocomposite beams. The governing equations are derived through Hamilton's principle and then solved by using the generalized differential quadrature method. Effects of SWNT volume fraction, foundation stiffness parameters, slenderness ratios, SWNT distribution and boundary conditions on natural frequency are estimated. Ke et al. [12] investigated the nonlinear vibration of aligned straight SWNT FG beams based on Timoshenko beam theory and von Karman geometric nonlinearity. The effect of the vibration amplitude, volume fraction of SWNT, ratio of length to thickness, boundary conditions and SWNT distribution were taken into account to characterize the nonlinear vibration of the beams. In light of von Karman geometric nonlinearity assumptions and the first-order shear deformation beam theory, Wu et al. [13] studied the nonlinear vibration of FG SWNT reinforced composite beams with initial imperfection. The Ritz method is applied to derive the nonlinear eigen frequency. Ansari et al. [14] dealt with the nonlinear vibration behavior of nanocomposite beams reinforced with SWNT based on the Timoshenko beam theory along with von Karman geometric nonlinearity. Poly methyl methacrylate (PMMA) is considered as the matrix. The vibration of cantilever FG SWNT beam subjected to compressive axial force is studied by Nejati et al. [15]. The two-dimensional elasticity theory and Hamilton’s principle are used to determine the stability and motion equations. These equations are discretized using the generalized differential quadrature method. The influence of graded agglomerated SWNT, and the effect of axial forces exerted on the natural frequencies of FG beam are investigated. Yas and Heshmati [16] worked on dynamics of FG nanocomposite beams reinforced with randomly oriented SWNT. The dynamic characteristics of the FG beam are predicted using Timoshenko and Euler-Bernoulli beam theories. It is found that under the action of moving load, FG SWNT beam with symmetrical distribution gives superior properties than that of unsymmetrical distribution.

To the author’s knowledge, the free vibration of FG SWNT reinforced Al-alloy composite beams, which represent an important industrial application, has not been investigated.

In a variety of dynamic problems, exact solutions may not be obtained, and one has to employ approximate methods. The Rayleigh-Ritz method is an approximate numerical method used extensively in several research sectors, but especially in the analysis of structural members [17]. The method can be used for both continuous and discrete systems. It is based on a linear expansion of the solution in terms of admissible functions [18]. In vibration problems, the frequencies are deduced from a quotient with potential energy being the numerator and kinetic energy function being the denominator. This quotient is called the Rayleigh quotient. The expansion coefficients are obtained using the principle of minimum potential energy [18].

Based on the classical beam theory (CBT), the Timoshenko beam theory (TBT) and the parabolic shear deformation beam theory (PSDBT), the present research focuses on the free vibration of FG SWNT reinforced Al-alloy composite beams. The Rayleigh-Ritz method is used to determine the frequencies.

The objective is to study the effects of SWNT volume fraction, SWNT distribution pattern, beam slenderness ratio and the BT on the natural frequencies of FG SWNT reinforced Al-alloy composite beams. To validate the present analysis, comparative studies are carried out with available results from the existing literature and with performed FE simulations.

The paper has the following outline. In Section 2, the homogenized properties of SWNT reinforced Al-alloy composite are determined using the two level (M-T, M-T) scheme. Section 3 details the mathematical modeling on vibration of randomly oriented FG SWNT reinforced Al-alloy composite beams based on the BT and the Rayleigh-Ritz method. Section 4 presents the numerical results of free vibration of FG SWNT reinforced Al-alloy composite beams using the mentioned BT and FE simulations. The validation of obtained results and parametric study are discussed in the same Section 4. Lastly, Section 5 summarizes the results and conclusions.

2. Material properties of FG SWNT reinforced Al-alloy composite beams

2.1. Mechanical properties of Al-alloy, SWNT and SWNT/Al-alloy composites

The Young’s modulus, the Poisson’s ratio and the density of Al-alloy taken in this paper are respectively; $E=$ 70 GPa, $\nu =$ 0.33 and $\rho =$ 2700 Kg/m³ [19] while the Young’s modulus and the Poisson's ratio of the homogenized graphene sheet that constitute the SWNT are determined by the author using a homogenization method based on the energy equivalence and have been found to be 2520 GPa and 0.25, respectively [7]. The density of the armchair SWNT with chiral index of (10, 10) is 1330 Kg/m³[20].

A mean field homogenization scheme named two-level (M-T/M-T) is selected to predict the mechanical properties of SWNT/Al-alloy composites.

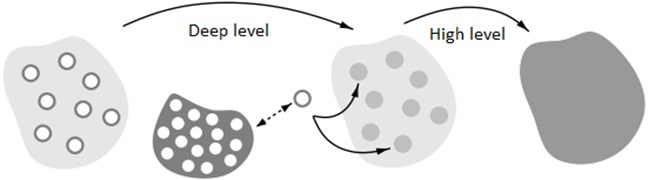
The two-level procedure was proposed by Friebel et al. [21] for coated inclusion-reinforced materials. The methodology is illustrated on Fig. 1. Each SWNT is seen (deep level) as a two-phase composite (graphene sheet with cavities) which, once homogenized, plays the role of a homogeneous reinforcement for the matrix material (high level). In the first level of the two-level procedure, the graphene matrix containing many small ellipsoidal cavities (having the same shapes and aspect ratios as the actual ones) is homogenized. The homogenization of the matrix material reinforced with homogeneous reinforcement is performed in the second level. In this paper, choosing Mori-Tanaka (M-T) for both levels, the scheme is labeled “two-level (M-T/M-T)”.

Fig. 1Schematic view of the two-level homogenization procedure for the effective properties of SWNT composites. For each level a two-phase homogenization model is required

The rule of mixture is adopted to determine the density of the mentioned composite. The variations of Young’s modulus, Poisson’s ratio and density, as a function of reinforcement volume fraction, $V$, of 3D randomly oriented and long SWNT/Al-alloy composites are reported in Table 1.

Interpretation: From Table 1, it is deduced that the reinforcing effect of SWNT is very important and as the SWNT volume fraction in the Al-alloy increases, the Young’s modulus increases rapidly. For an Al-alloy comprising 10 % of SWNT, the Young’s modulus, $E$, is increased by a factor of 1.4 but the Poisson’s ratio and the density decreases by a factor of 1.06 and 1.05, respectively.

Table 1SWNT/Al-alloy composite with 3D randomly oriented and long reinforcements

$V$ (%)	$E$ (GPa)	${\rm N}$	$\rho$ (Kg/m3)
0	70	0.33	2700
1	72.88	0.327	2686.3
3	78.60	0.323	2658.9
5	84.28	0.319	2631.5
10	98.33	0.311	2563

2.2. Properties of FG materials

A straight simply supported FG beam of length $L$, width $b$, and thickness $h$ is shown in Fig. 2.

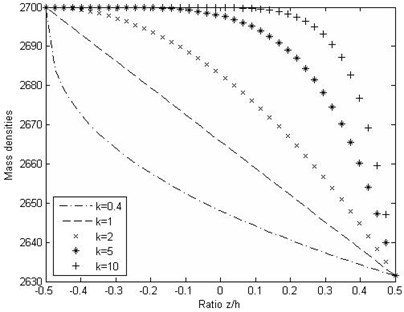
In the present study, the volume fraction of SWNT is assumed to be graded in the thickness direction so that the material properties of the beam vary continuously according to power-law form as shown in Figs. 3, 4.

Fig. 2Beam element with Cartesian coordinates

Fig. 3Variation of Young’s modulus through the thickness direction of the beam

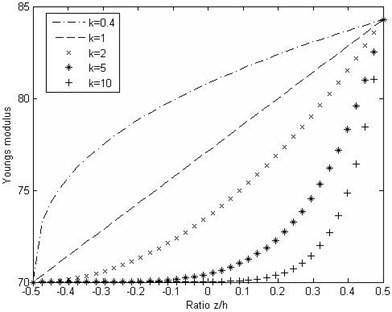
Fig. 4Variation of mass density through the thickness direction of the beam

The considered power-law variation is:

1

$P\left(z\right)=(P_c-P_a){\left(\frac{z}{h}+\frac{1}{2}\right)}^k+P_a.$

$P_a$ and $P_c$ stand for the values of the material properties of Al-alloy and SWNT/Al-alloy composite, respectively. Therefore, the bottom surface of the beam is Al-alloy, whereas its top surface is SWNT reinforced Al-alloy composite. Hereafter, for the top surface, 5 % and 10 % SWNT volume fractions are considered.

3. Numerical modeling and formulation

Let’s assume the deformation of FG beam in the $x$-$z$ plane and designate the displacement components in the $x$ and $z$ directions by $u_x$ and $u_z$, respectively. Based on the BT, the axial and transverse displacement of any point of the beam are respectively:

where $u$ and $w$ denote the axial and the transverse displacement of any point on the neutral axis respectively, while $v$ represents the effect of transverse shear strain on the neutral axis. $\varphi \left(z\right)$ stands for the shape function and ($x$) indicates the partial derivative in terms of $x$. The present study is concerned with classical beam theory, CBT, Timoshenko beam theory, TBT, and parabolic shear deformation beam theory, PSDBT [22]. $\varphi \left(z\right)$ for these BT are given as below [23]:

The strain energy, $S$, and the kinetic energy, $T$, of the beam at any moment are given as:

where $A$ and $\rho$ are the area of cross-section and the mass density of the beam, respectively. ${\sigma }_{xx}$, ${\tau }_{xz}$, ${\epsilon }_{xx}$ and ${\gamma }_{xz}$ denote the normal stress, the shear stress, the normal strain and the shear strain, respectively

Assuming the harmonic displacement components:

where $U\left(x\right)$, $V\left(x\right)$ and $W\left(x\right)$ are the respective amplitudes of the displacement components and $\mathrm{\omega }$ is the natural frequency.

The substitution of the expressions of displacement components into Eqs. (3), (4) yields the maximum strain energy, $S_{max}$, and the maximum kinetic energy, $T_{max}$ as:

where:

and:

The transformed stiffness constants are:

Using the Rayleigh-Ritz method, the amplitudes of vibration can be expanded in terms of polynomial functions by the following series as:

where $c_i$, $d_j$ and $e_k$ are constants to be determined and ${\phi }_i$, ${\psi }_j$ and ${\chi }_k$ are known functions that must satisfy the boundary conditions of the problem. These admissible functions can be written as:

For simply supported beams: $f=x^2-(L/2{)}^2$ [24].

Consequently, by equating $S_{max}$ and $T_{max}$, the Rayleigh Quotient ${\omega }^2$ can be deduced. The principle of minimum potential energy implies that the partial derivatives of the Rayleigh Quotient with respect to each of the constants $c_i$, $d_j$, and $e_k$ are nul. Accordingly, one can write:

Eq. (10) represents a set of 3$n$ algebric equations in 3$n$ unknowns $c_1$, $c_n$, $d_1$, $d_n$, and $e_1$, $e_n$. Its resolution requires considerable computation duration. Eq. (10) is then written in matricial form as:

where [$K$] and [$M$] are the dynamic stiffness and inertia matrices, respectively and [$\mathrm{\Delta }$] is the vector of unknown coefficients. The frequency parameters for free vibration problem are given by $\lambda$. Frequency parameters determined from this eigenvalue problem are investigated in the next section with the mentioned BT. Validation with the existing literature and with FE results are also reported.

4. Numerical results

In this section, the first three frequency parameters for the free vibration of simply supported FG beam are investigated using the above-mentioned beam theories. The effect of the distribution fashion of the SWNT volume fraction throughout the beam thickness, the effect of SWNT content in the beam top surface and the beam slenderness ratio are analyzed. The frequency parameter is expressed as:

4.1. Convergence and validation of the analysis

4.1.1. Convergence analysis

In Tables 2-4, the convergence behavior of first three frequency parameters of simply supported FG beam with $L/h=$ 5 and 5 % SWNT volume fraction on the beam top surface are reported. The increase in the number n of polynomial items in the admissible functions is checked using CBT, TBT and PSDBT.

Table 2Convergence of first three frequency parameters of simply supported FG SWNT/Al-alloy beams using CBT for (L/h= 5) and 5 % SWNT content on the beam top surface

CBT	Al-alloy			$k=$ 5
$N$	${\lambda }_1$	${\lambda }_2$	${\lambda }_3$	${\lambda }_1$	${\lambda }_2$	${\lambda }_3$
2	3.2956	14.3779	16.7497	3.4988	14.7756	17.1114
3	2.9706	14.3779	16.6402	3.0621	14.774	17.0014
4	2.9706	11.3964	16.6401	3.0621	11.7342	16.9624
5	2.9697	11.3964	16.6401	3.0612	11.7342	16.9623
6	2.9697	11.3491	16.6401	3.0612	11.6859	16.9618
7	2.9697	11.3491	16.6401	3.0612	11.6859	16.9618
8	2.9697	11.3491	16.6401	3.0612	11.6857	16.9618
9	2.9697	11.3491	16.6401	3.0612	11.6857	16.9618
10	2.9697	11.3491	16.6401	3.0612	11.6857	16.9618

Table 3Convergence of first three frequency parameters of simply supported FG SWNT/Al-alloy beams using TBT for (L/h= 5) and 5 % SWNT content on the beam top surface

TBT	Al-alloy			$k=$ 5
$n$	${\lambda }_1$	${\lambda }_2$	${\lambda }_3$	${\lambda }_1$	${\lambda }_2$	${\lambda }_3$
2	3.2955	13.5286	16.7497	3.3975	14.0428	17.0927
3	2.8384	13.4888	16.6402	2.9449	14.0038	16.9816
4	2.8300	9.5017	16.6402	2.9364	10.0211	16.9529
5	2.8225	9.4253	16.5059	2.9304	9.9397	16.9525
6	2.8216	9.4035	16.3217	2.9295	9.9230	16.9524
7	2.8165	9.3492	16.2094	2.9019	9.6689	16.7125
8	2.8163	9.3433	16.2061	2.9016	9.6467	16.6947
9	2.8163	9.3431	16.2061	2.8999	9.6458	16.6947
10	2.8163	9.3428	16.2060	2.8998	9.6455	16.6948

It is observed that increasing the number of polynomial items, n, improves the accuracy of results and leads to convergent solutions at $n=$ 10. Hence $n=$ 10 is used in the following numerical calculations.

4.1.2. Validation of the analysis

The validation analysis is done through direct comparison with previously published results and with finite element results obtained by using commercial finite element software package ANSYS [25].

4.1.2.1. Comparison with available results

In order to check the above written formulation, the first three frequency parameters of simply supported FG beams are compared with [26] for slenderness ratios ($L/h=$ 20, 50 and 100) and power-law index ($k=$ 0, 0.1 and 0.2). The material properties of steel are $E=$ 210 GPa; $\rho =$ 2700 Kg/m³ and those of Alumina (Al₂O₃) are $E=$ 390 GPa; $\rho =$ 3960 Kg/m³. Table 5 shows that the results given by the BT are very close to those available in [26].

Table 4Convergence of first three frequency parameters of simply supported FG SWNT/Al-alloy beams using PSDBT for (L/h= 5) and 5 % SWNT content on the beam top surface

PSDBT	Al-alloy			$k=$ 5
$n$	${\lambda }_1$	${\lambda }_2$	${\lambda }_3$	${\lambda }_1$	${\lambda }_2$	${\lambda }_3$
2	3.2955	13.5290	16.7497	3.3975	13.8882	17.09
3	2.8392	13.4896	16.5612	2.9222	13.8474	16.9789
4	2.8308	9.5187	16.4352	2.9136	9.7509	16.9519
5	2.8238	9.4449	16.3954	2.9059	9.6756	16.9328
6	2.8230	9.4275	16.3915	2.9051	9.6569	16.7576
7	2.8187	9.4247	16.3895	2.9011	9.6552	16.7579
8	2.8172	9.3961	16.3821	2.9008	9.6546	16.7575
9	2.8169	9.3957	16.3805	2.9005	9.6541	16.7574
10	2.8168	9.3955	16.3802	2.9005	9.6539	16.7574

Table 5First three frequency parameters. A comparison with data after Amal et al. [26]

$L/h-k$		$L/h-k$		$L/h-k$		$L/h-k$
20-0		50-0		100-0.1		100-0.2
CBT	Ref	CBT	Ref	PSDBT	Ref	TBT	Ref
4.4019	4.3425	4.4038	4.3444	4.2526	4.2838	4.1372	4.2336
8.7903	8.6716	8.8054	8.6866	8.5009	8.5671	8.265	8.4666
13.152	12.975	13.2027	13.025	12.748	12.849	12.3952	12.699

4.1.2.2. Comparison with finite element resulats

As already mentioned, the material properties of the FG beam vary continuously throughout its thickness. The beam bottom surface is made of Al-alloy, whereas the top one is made of SWNT/Al-alloy composite. In order to model the FG beam, the numerical model has been divided into several layers so that the changes in properties can be made. Each layer has the finite portion of the thickness and treated like isotropic material. Material properties of each layer have been calculated at its mid-plane by using the chosen power-law distribution. To study the convergence analysis, various number of layers has been taken; 2, 4, 8 and 10. The FE modeling has been performed using ANSYS (2013). Higher order 3-D, 10-node elements (SOLID187) has been used for modeling of FG beams. SOLID187 has a quadratic displacement behavior. This element has three degrees of freedom at each node: translations in the nodal $x$, $y$, and $z$ directions. To simulate the pin support, the $x$, $y$ and $z$ bottom edge displacements are constrained while the roller support is free to move in the axial direction. 208797 elements with 292166 nodes are needed. Fig. 5 shows the fundamental mode shape for 10 layers of simply supported FG SWNT reinforced Al-alloy composite beam. The materials used for modeling and analysis of beams are Al-alloy and Al-alloy comprising 10 % of SWNT. Their properties are given in the second and sixth lines of Table 1.

Fig. 5Fundamental mode shape for 10 layers of FG beam

Table 6 reports the fundamental frequency parameters delivered by the FE analysis. Table 7 exposes the comparison between FE results and those obtained using the formulation explained in Section 3.

Interpretation: It can be interpreted that for different power-law distributions, the number of layers has a great influence on the fundamental frequencies of the modeled FG beam. From Table 6, one can consider that the convergence is reached for 10 layers. The FE results gotten for ten layers beams are confronted against those obtained using CBT, TBT and PSDBT. It is found that the present results are very close (see Table 7). The satisfactory results concerning the frequency parameters give confidence in the predictions reported in next sections.

Table 6FE predictions of fundamental frequency parameters of simply supported FG SWNT/Al-alloy beams with (L/h= 30) and different power-law exponents (k)

$N$	$k=$ 0	$k=$ 0.4	$k=$ 1	$k=$ 2	$k=$ 5	$k=$ 10	Al-alloy
2	3.4668	3.3045	3.1576	3.0405	2.9247	2.8680	2.8500
4	3.4668	3.2825	3.1509	3.0686	2.9839	2.9184	2.8500
8	3.4668	3.2727	3.1496	3.0781	3.0057	2.9499	2.8500
10	3.4668	3.2718	3.1496	3.0795	3.0084	2.9546	2.8500

Table 7Comparison of fundamental frequency parameters of simply supported FG SWNT/Al-alloy beams with FE results for different power-law exponents and slenderness ratio L/h=30

Theory	$k=$ 0	$k=$ 0.4	$k=$ 1	$k=$ 2	$k=$ 5	$k=$ 10	Al-alloy
CBT	3.6698	3.4645	3.3477	3.2764	3.1982	3.1406	3.0168
TBT	3.6642	3.4593	3.3426	3.2713	3.1931	3.1355	2.9726
PSDBT	3.6642	3.4593	3.3426	3.2713	3.1930	3.1355	2.9726
FE	3.4668	3.2718	3.1496	3.0795	3.0084	2.9546	2.8500

5. Conclusions

The free vibration of simply supported FG SWNT/Al-alloy beam was investigated based on various BT using the Rayleigh-Ritz method. This helps fill in a gap in the literature where the available mechanical results about SWNT reinforced Al-alloy composites did not concern the free vibration. The Rayleigh-Ritz method is found to be efficient when compared to FE simulations. The objective of improving the dynamic characteristics of Al-alloy in order to prevent problems such as failures associated with resonance and fatigue is achieved by reinforcing with functionally graded SWNT. Reinforcement with SWNT allows a significant increase of the Al-alloy dynamic properties without compromising other factors such as mass of the structure. The improvement of the natural frequencies of beams made of AL-alloy was attained by increasing the amount of the reinforcement, increasing the slenderness ratio and decreasing the power-law exponent.